电力系统短期负荷新型Volterra预测模型研究
2014-08-08惠萌刘盼芝
惠萌,刘盼芝
(长安大学电子与控制工程学院, 710064, 西安)
电力系统短期负荷新型Volterra预测模型研究
惠萌,刘盼芝
(长安大学电子与控制工程学院, 710064, 西安)
针对电力系统负荷短时预测问题,从分析负荷数据的混沌特性入手,利用相空间重构理论对负荷数据进行重构,构建了一种新型的Volterra模型对电力系统负荷进行预测。该模型采用二次线性微分方程方法对原Volterra级数进行变换,与以往Volterra级数相比,该模型无截断误差,包含了系统更多精确的信息。最后,以某地区实际用电负荷数据为对象进行验证,结果表明:该模型2d和4d用电负荷预测结果和实际结果误差不超过5%,完全能够满足电力调度需求,同时也为电力公司制定经济模型和实时电价调整提供了理论支持。
电力系统;短期负荷;Volterra预测模型
电力系统日常运行的一项重要工作就是短期负荷预测,预测结果是电力调度和经济运行的依据。短期负荷预测主要用来预测未来几小时或者几天的负荷,电力公司要根据准确、快速的负荷预测调整其运行模式和实时电价来增强其市场竞争力。
电力系统短时负荷的预测一直是研究的热点,各种新理论新方法相继应用到这项研究中,常见的方法有时间序列法[1-2]、神经网络法[3-4]、卡尔曼模型法[5]、遗传优化法[6]、支持向量机法[7]、粒子群算法[8]等。然而,时间序列法在使用低阶预测模型时精度低而使用高阶模型时参数估计困难;神经网络法存在输入数据的选取及网络结构不易确定等问题;卡尔曼模型法的状态和测量方程的推导很困难。文献[9]中已经证明电力负荷数据序列存在混沌特性,因此利用混沌理论来分析电力系统相关特性是目前研究的一个热点方向。具备混沌特性的电力负荷时间序列数据可以通过相空间重构理论来进行重构,将单变量的时间序列嵌入到重构的相空间中,得到的状态轨迹将包含原有状态轨迹的特征,根据这一特点可以对电力负荷时间序列数据进行预测。Volterra级数能以任意精度逼近大多数非线性系统,是非线性系统研究中的重要手段,但在以往研究中所使用的Volterra模型均为截断模型,此模型会导致误差。
本文以某地区实际用电负荷数据为对象,利用互信息法确定延迟时间后,再使用CAO方法确定最佳嵌入维数,完成负荷时间序列的相空间重构。采用GP算法计算吸引子关联维数,通过改进小数据量法计算最大Lyapunov指数来判别该用电负荷时间序列的混沌特性。本文构建了一种新型的局域线性化Volterra预测模型,与以往模型相比,该模型不用截断,包含了更多精确的系统信息。将该模型应用到短时用电负荷时间序列的预测中,模型的预测结果能够为电力调度和经济运行提供理论支持。
1 非线性系统局部线性化基础
对于单输入多输出系统
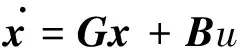
(1)
式中:x∈Rn为系统状态向量;u∈R为输入信号。
假设1、2阶自治系统为
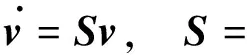

(2)
输入信号
u=acos(ωt),ω∈R
设v=[v1,v2]T,v∈R2,系统矩阵S可被分解为

(3)
式中:Q为酉矩阵;系统闭环解为v(t)=eStv(0),即

(4)
同样,输入信号u=acos(ωt)可改写为
u=Lv,L=[a0]
(5)
综合式(1)~(5)得到

(6)
若λi(G)-λj(S)≠0(i=1,2,…,n;j=1,2),则Sylvester方程
G∏+BL=∏S, ∏∈Rn×2
(7)
存在唯一解。
假设k阶单位阵为Ik,可以得到

(8)
进而可得式(6)所示系统解
x(t)-∏v(t)=eGt(x(0)-∏v(0))
(9)
系统解主要受初始状态x(0)=∏v(0)和稳态解∏v(t)影响。如果x(0)=∏v(0),则系统无论G是否稳定,系统解为周期稳态解。
2 Volterra预测模型
根据Volterra理论[10],非线性系统的响应可以被分解为一系列齐次非线性系统,即系统响应x(t)可以表示为
(10)
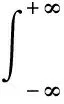
σn)u(t-σ1),…,u(t-σn)dσ1,…,dσn
(11)
式中:hn(σ1,…,σn)为n阶Volterra核函数。通过求解此核函数,对混沌系统的轨道进行逼近,从而实现对原系统的预测。考虑到混沌系统具有强烈的非线性特点,Volterra非线性映射函数利用自身高阶矩信息,对混沌系统的近似更准确,预测结果更可靠。但是,在实际应用中随着σ的增加,Volterra模型的滤波器个数会呈幂指数增加,计算量也随之急剧增长,这给工程实践带来很大的困难。在实际应用中往往采取截断方式,但这样会丢失预测系统的部分信息,造成预测结果的误差。
文献[11]指出,任何常微分方程都可以被改写为二次线性微分方程,即
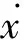
(12)
广义多项式系统也可以改写为
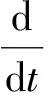
D1xu+D2(x⊗x)u+Bu
(13)
如果式(1)所示系统输入为au,则系统响应为
x(t)=ax1(t)+a2x2(t)+a3x3(t)+…
(14)
令a=1,将式(14)代入式(12)得
(15)
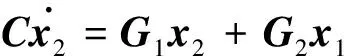
(16)
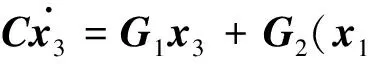
D1x2u+D2(x1⊗x1)u
(17)
将式(5)所示输入信号带入式(15),可得到系统稳态解为x1(t)=∏1v(t),∏1∈Rn×2,解Sylvester方程
G1∏1+B1=∏1S,B1=BL
(18)
如果矩阵G1的特征值和矩阵S的虚特征值之和不为0,则∏1存在唯一解。初始值x1(0)=∏1v(0)及输入信号u=acos(ωt)时,系统稳态解x1(t)=∏1v(t)。稳态解中系统时间参数可以忽略,即x1=∏1v。
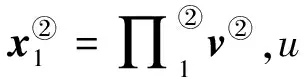
⊗L)]v②≜
G1x2+B2v②
(19)
v②导数为
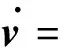
I2⊗S+S⊗I2)v②≜S2v②
(20)
式(19)、(20)构成了另一个Sylvester方程,方程中参数∏2∈Rn×4未知,新的Sylvester方程可表示为
G1∏2+B2=∏2S2
(21)
系统的稳态解x2=∏2v②。采用同样的方法可以得到x1⊗x2=(∏1⊗∏2)v③,x2u=(∏2⊗L)v③。
令
B3=G2(∏1⊗∏2+∏2⊗∏1)+D1(∏2⊗L)+
D2L∏1②;S3=S⊗I4+I2⊗S⊗I2+I4⊗S
则第3个Sylvester方程为
G1∏3+B3=∏3S3
(22)
稳态解为x3=∏3v③。
通过以上分析,可以看出非线性系统稳态解为xk=∏kvk,∏k∈Rn×2k,k=1,2…,系统解可以写为
∏1v(t)+∏2v②(t)+∏3v③(t)+…
(23)
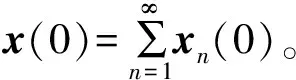
为了简化该模型算法编程,将电力负荷数据进行归一化处理
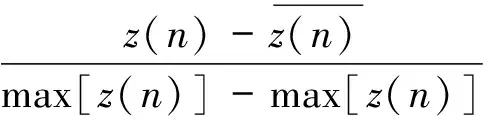
(24)
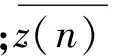
3 相空间重构
3.1 电力负荷数据
本文研究对象为某地区2014年1月1日到2月17日用电负荷数据,如图1所示。每小时记录一次用电负荷,共得到1 104组数据。
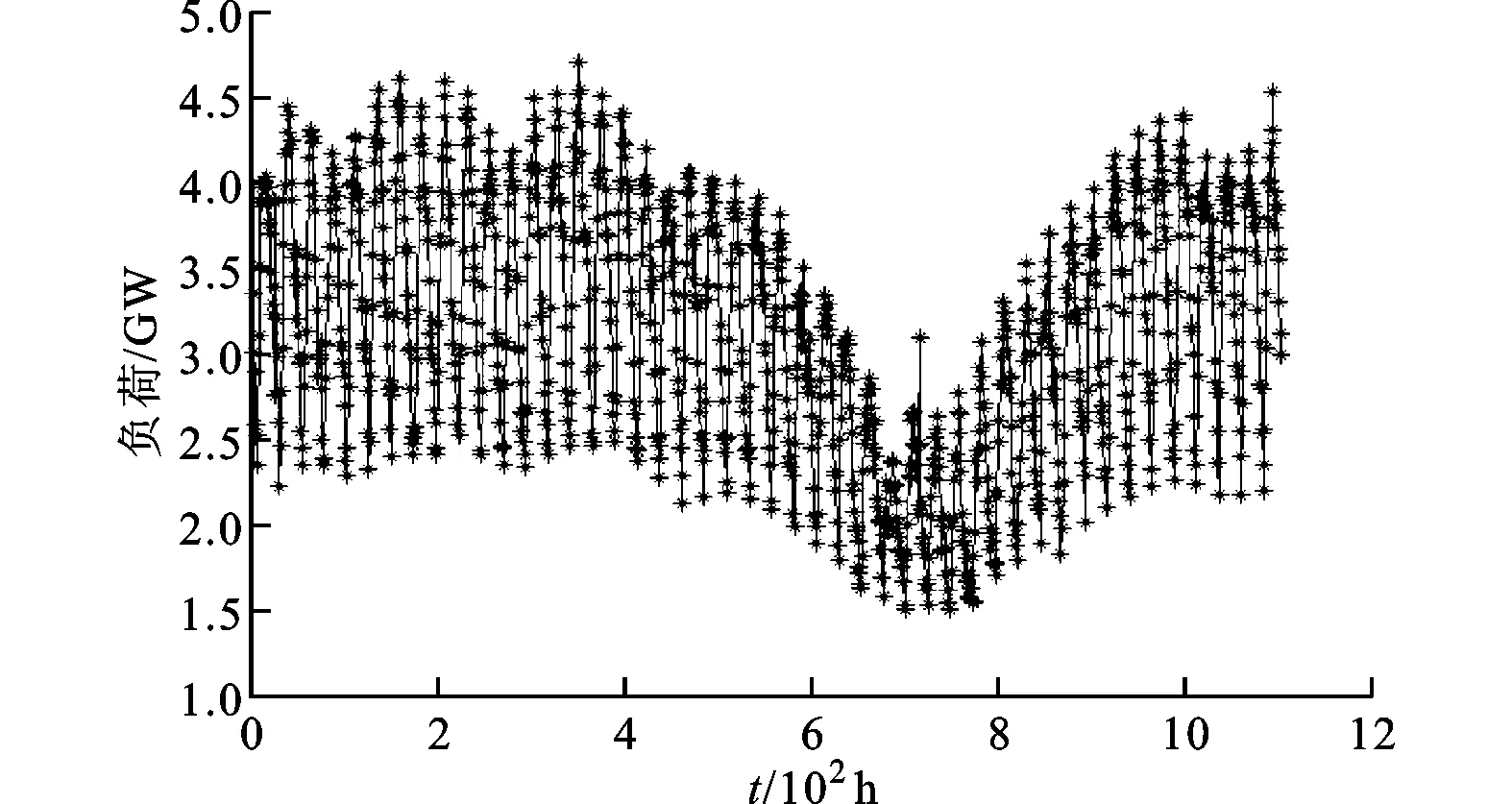
图1 某地区电力负荷数据
3.2 延迟时间
荷兰数学家Takens所述定理中指出:可以找到一个合适的嵌入维数,如果满足m≥2d+1(d为动力系统维数),则可以在相空间中把原系统的轨迹恢复出来[12]。根据Takens定理,将采集到的负荷数据序列嵌入到一个延迟时间为τ的m维相空间中,就可以通过得到的系统来预测未来短期负荷的变化。因此,τ和m的选择是相空间重构的重要工作。
互信息法克服了自相关法不能应用于高维混沌系统的缺点,是确定τ的一种应用比较广的方法。互信息法以互信息函数第一个最小值点为τ。如混沌时间序列x1,x2,…,延迟时间为τ,嵌入维数为m,则重构的相空间为
S(t)=(s0(t),s1(t),…,sn(t))
(25)
式中:sn(t)=x(t+(m-1)τ),n=1,2…N。系统对变量x的平均信息量为系统的熵
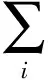
(26)
对于一般情况,互信息为
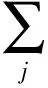
H(X0,X1,…,Xn)]
(27)
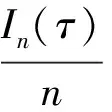
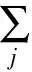
(28)
利用互信息法估计交通流数据延迟时间τ如图2所示,在τ=5时系统出现局部最小值,所以最佳延迟时间为5。
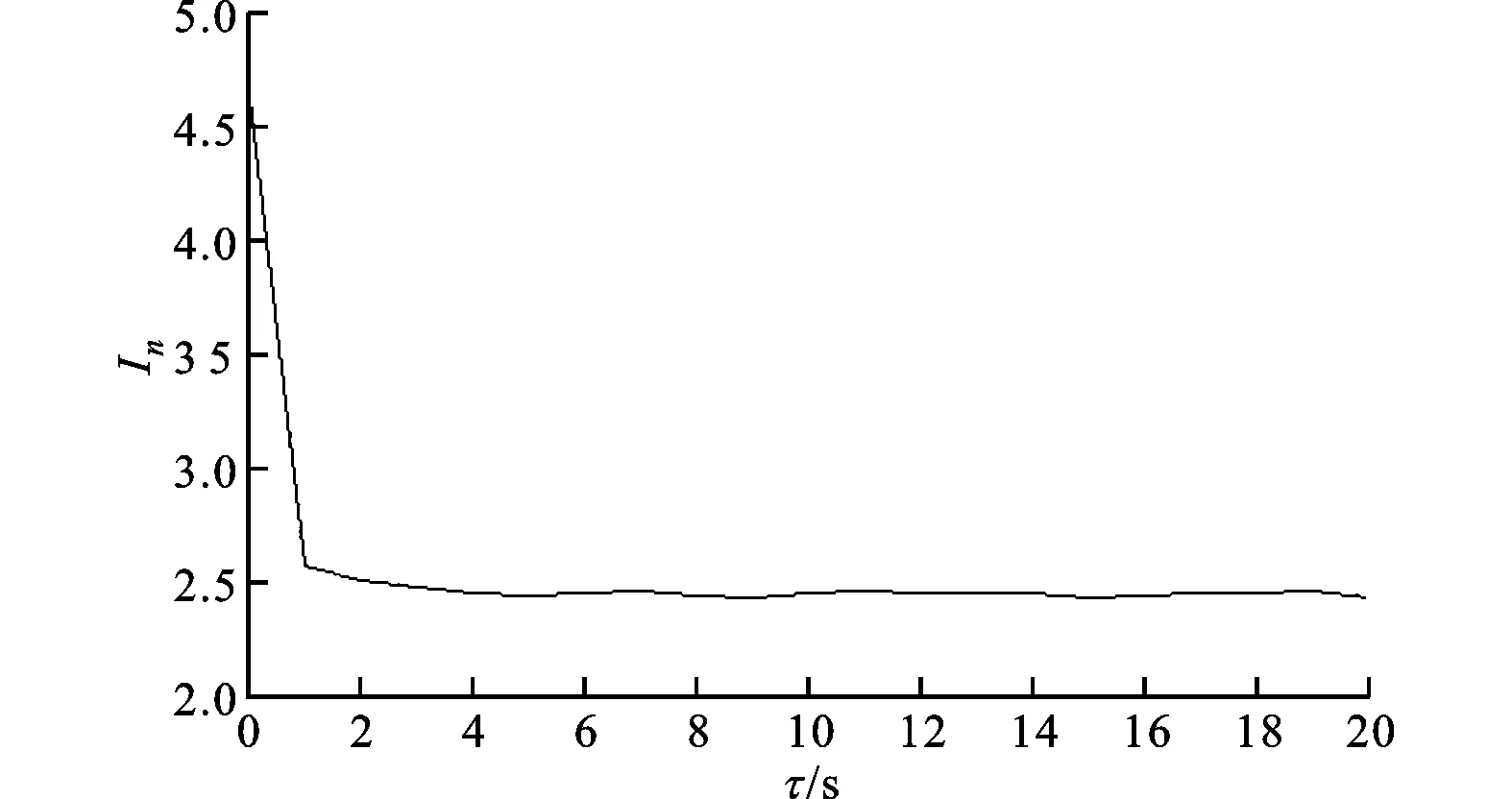
图2 采用互信息法确定延迟时间
3.3 嵌入维数
嵌入维数的选取有多种方法,主要分为伪邻近点方法、基于预测性能的方法、基于统计不变量的算法、基于奇异值分解的方法4类[13]。按照以往算法,τ和m的选取是独立的,但是有研究指出,嵌入维数的选取和延迟时间是相互影响的[14]。影响相空间质量的主要因素是嵌入维数和延迟时间的嵌入窗τw=(m-1)τ,考虑这一因素常用的方法有C—C法。
对式(25)重构相空间中的各点,其关联积分
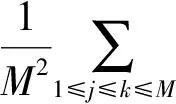
(29)
式中:N为时间序列长度;r为邻域半径;θ为Heaviside函数。
系统关联维数为
(30)
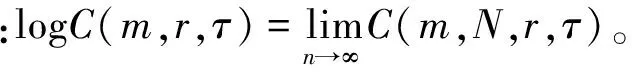
S(m,N,r,τ)=C(m,N,r,τ)-Cm(m,N,r,τ)
(31)
式中:S(m,N,r,τ)反映了时间序列的自相关性。最佳延迟时间可以选为S(m,N,r,τ)的第一个0点或者对所有半径r差别最小的时间点。定义最大、最小2个半径的差为
ΔS(m,τ)=max[S(m,N,rj,τ)]-
min[S(m,N,rk,τ)]
(32)
式中:j≠k;ΔS(m,τ)度量了所有半径r的最大偏差。
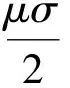
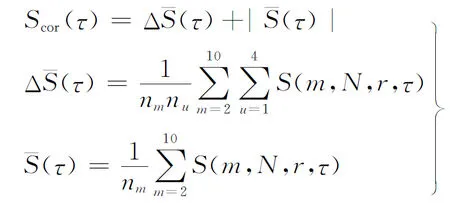
(33)
寻找Scor(τ)极小点为嵌入窗τ,进而可以得到最佳嵌入维数m。根据C—C算法得到的电力负荷数据S(m,N,r,τ)曲线如图3所示。由图3可以得到,最佳延迟时间为5,与利用互信息法得到的最佳延迟时间一致,最佳嵌入维数为14。
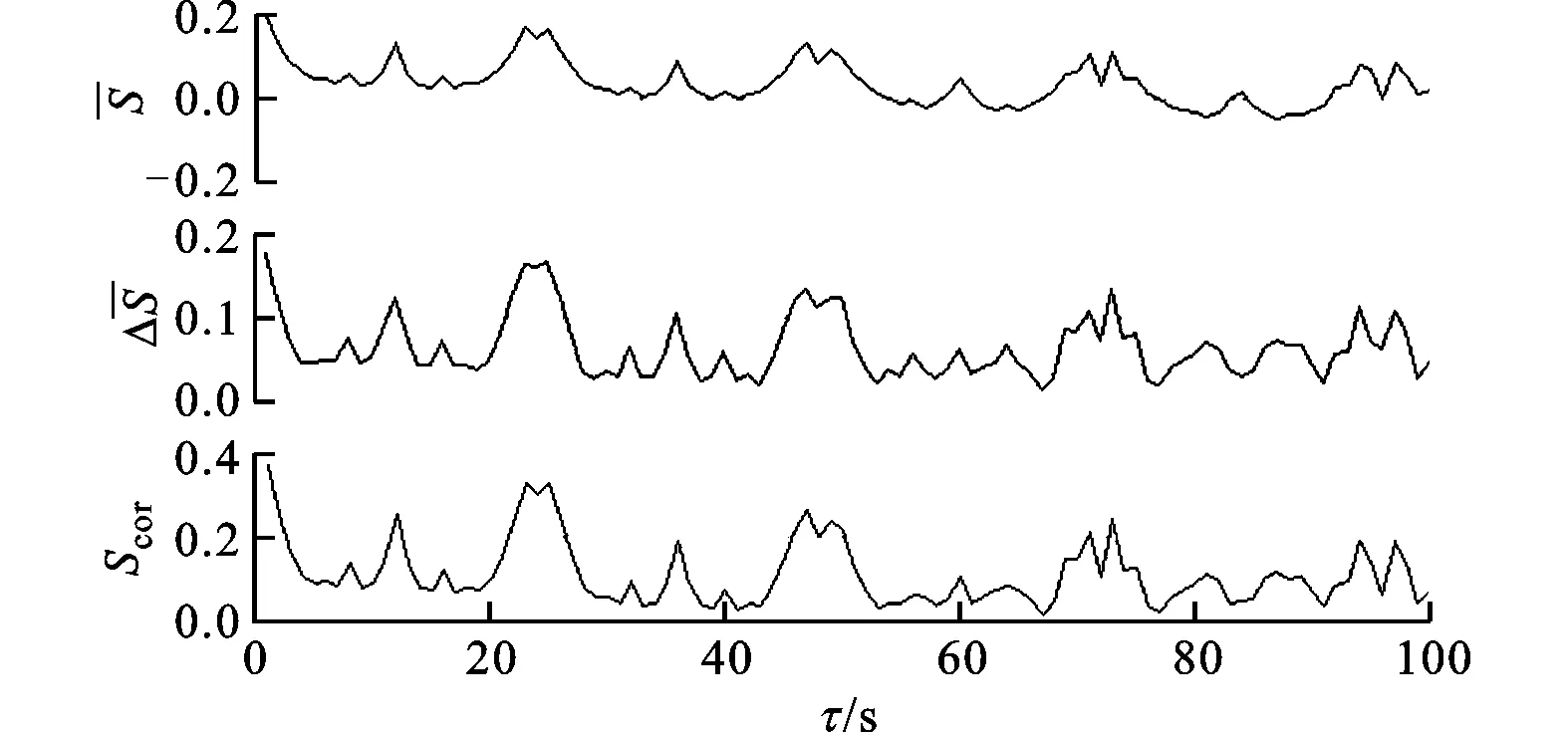
图3 采用C—C算法计算最佳嵌入维数
3.4 电力负荷数据混沌特性识别
电力系统负荷数据是否具有混沌特性是能否按照改进Volterra模型进行预测的决定因素。本文利用李雅普诺夫指数法判断负荷数据的混沌特性,李雅普诺夫指数变化曲线如图4所示。
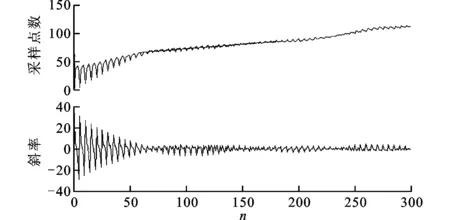
图4 李雅普诺夫指数变化趋势
从图4可以得到,电力负荷最大李雅普诺夫指数为0.1601,大于0,说明该数据时间序列具备混沌特性。
4 负荷预测实验
根据上述分析,对某地区电力系统负荷数据进行相空间重构,m=14,τ=5。分别对2014年2月14日到2月17日及2月16日到2月17日的用电数据进行预测,得到的预测结果如图5和图6所示。
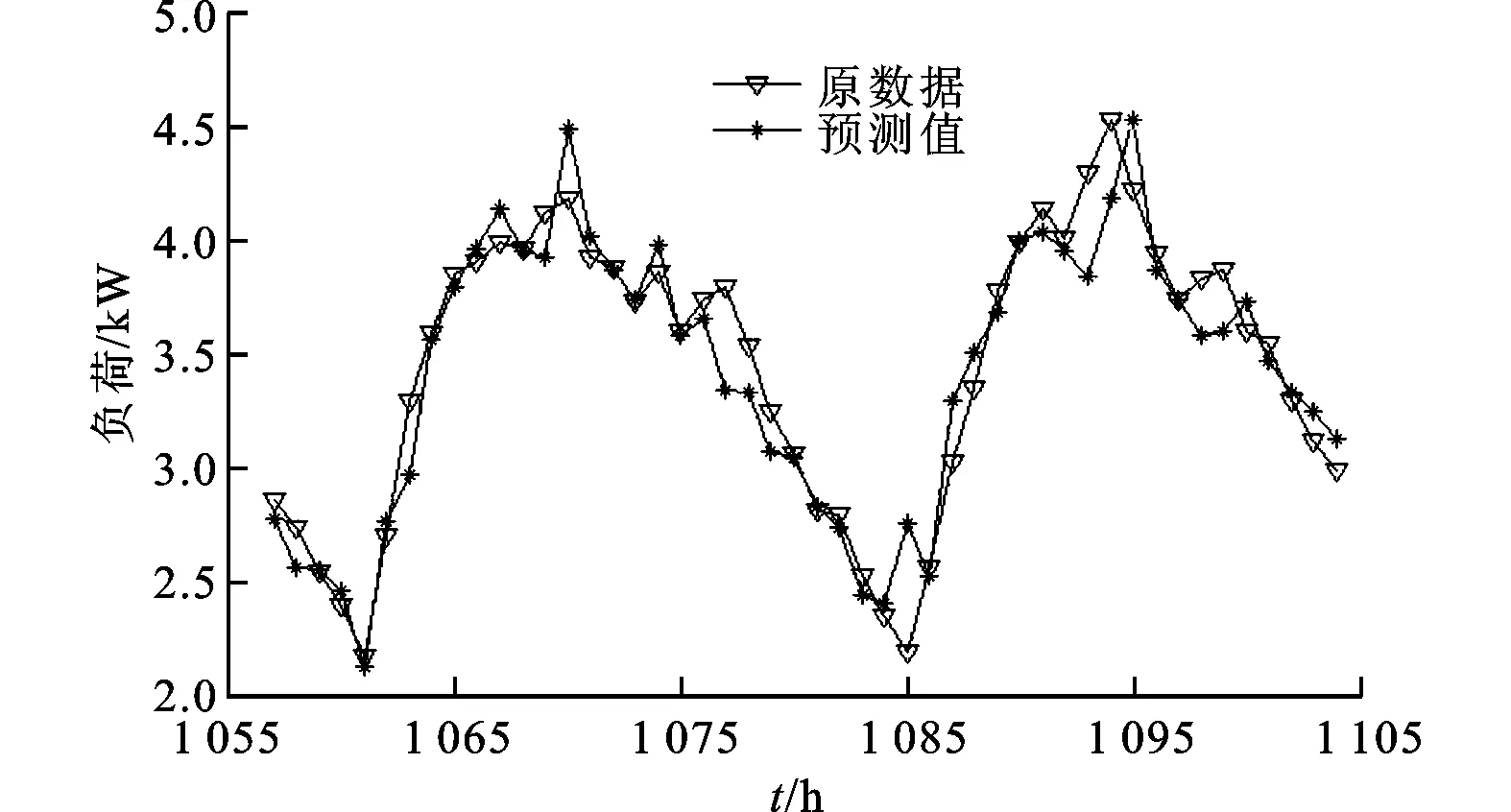
图5 2月16日到2月17日用电负荷预测
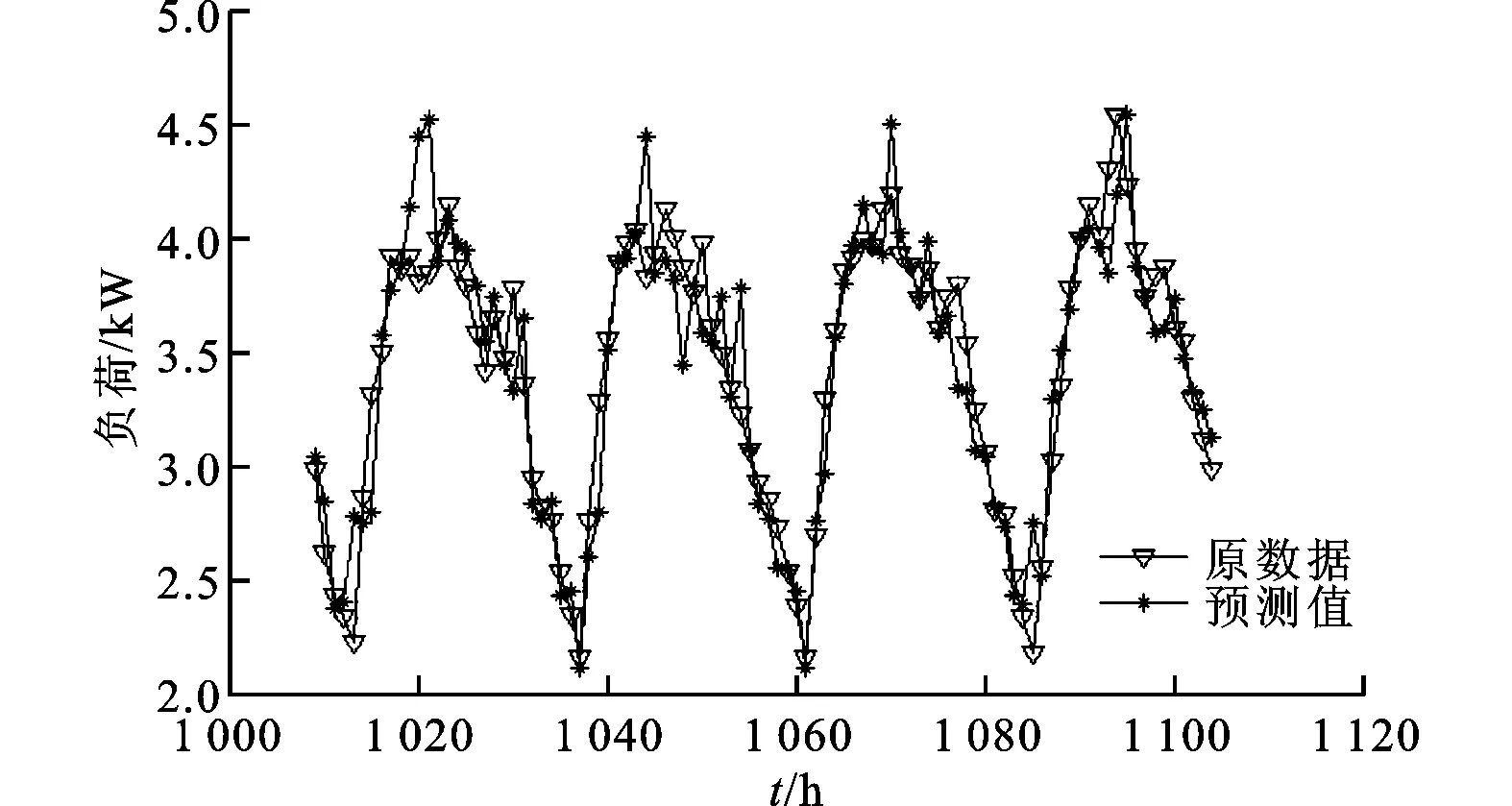
图6 2月14日到2月17日用电负荷预测
根据预测结果计算平均绝对百分比误差EMAP,4d预测结果的EMAP=4.83%,2d预测结果的EMAP=3.98%,预测结果误差最大均不超过5%,预测精度完全能满足电力调度的需求。
5 结 论
电力负荷预测是电力调度及电厂电价调整的基础,本文在分析电力负荷数据混沌特性的基础上,利用相空间重构理论对负荷数据进行了重构,进而利用改进的Volterra预测模型对负荷数据进行了预测。该模型避免了以往泰勒展开模型的截断误差,包含了更多的系统信息。通过对某地4d和2d的实际负荷数据进行预测实验,结果表明EMAP小于5%,能够满足电力调度的需求。
[1] 郑永康, 陈维荣, 蒋刚, 等. 一种模糊支持向量的负荷混沌时间序列预测法 [J]. 电力系统及其自动化学报, 2007, 19(6): 48-52.
ZHENG Yongkang, CHEN Weirong, JIANG Gang, et al. Chaotic time series method for load forecasting based on fuzzy support vector [J]. Proceedings of the CSU-EPSA, 2007, 19(6): 48-52.
[2] 雷绍兰, 孙才新, 周湶, 等. 电力短期负荷的多变量时间序列线性回归预测方法研究 [J]. 中国电机工程学报, 2006, 26(2): 25-29.
LEI Shaolan, SUN Caixin, ZHOU Quan, et al. The research of local linear model of short-term electrical load on multivariate time series [J]. Proceedings of the CSEE, 2006, 26(2): 25-29.
[3] 向峥嵘, 王学平. 基于小波-神经网络的电力系统短期负荷预测 [J]. 系统仿真学报, 2008, 20(18): 5018-5020.
XIANG Zhengrong, WANG Xueping. Forecasting approach to short-time load using wavelet decomposition and artificial neural network [J]. Journal of System Simulation, 2008, 20(18): 5018-5020.
[4] 兰华, 常家宁, 周凌, 等. 基于局部均值分解与神经网络的短期负荷预测 [J]. 电测与仪表, 2012, 49(1): 48-51.
LAN Hua, CHANG Jianing, ZHOU Ling, et al. Power system short-term load forecasting based on local mean decomposition and artificial neural network [J]. Electrical Measurement & Instrumentation, 2012, 49(1): 48-51.
[5] 魏少岩, 吴俊勇. 基于灰色模型和Kalman平滑器的多母线短期负荷预测 [J]. 电工技术学报, 2010, 25(2): 158-162.
WEI Shaoyan, WU Junyong. Short-term bus load forecasting based on grey model and Kalman smoother [J]. Transactions of China Electrotechnical Society, 2010, 25(2): 158-162.
[6] 冯丽, 邱家驹. 基于模糊多目标遗传优化算法的节假日电力负荷预测 [J]. 中国电机工程学报, 2005, 25(10): 29-34.
FENG Li, QIU Jiaju. Short-term load forecasting for anomalous days based on fuzzy multi-objective genetic optimization algorithm [J]. Proceedings of the CSEE, 2005, 25(10): 29-34.
[7] 谢宏, 魏江平, 刘鹤立. 短期负荷预测中支持向量机模型的参数选取和优化方法 [J]. 中国电机工程学报, 2006, 26(22): 17-22.
XIE Hong, WEI Jiangping, LIU Heli. Parameter selection and optimization method of SVM model for short-term load forecasting [J]. Proceedings of the CSEE, 2006, 26(22): 17-22.
[8] 蔡金锭, 付中云. 粒子群神经网络混合算法在负荷预测中的应用 [J]. 高电压技术, 2007, 33(5): 90-93.
CAI Jinding, FU Zhongyun. Application of particle group and neural network hybrid algorithm in load forecast [J]. High Voltage Engineering, 2007, 33(5): 90-93.
[9] 岳毅宏, 韩文秀, 张伟波. 基于关联度的混沌序列局域加权线性回归预测法 [J]. 中国电机工程学报, 2004, 24(11): 19-22.
YUE Yihong, HAN Wenxiu, ZHANG Weibo. Local adding-weight linear regression forecasting method of chaotic series based on degree of incidence [J]. Proceedings of the CSEE, 2004, 24(11): 19-22.
[10]杜杰, 曹一家, 刘志坚, 等. 混沌时间序列的局域高阶Volterra滤波器多步预测模型 [J]. 物理学报, 2009, 58(9): 5997-6005.
DU Jie, CAO Yijia, LIU Zhijian, et al. Local higher-order Volterra filter multi-step predication model for chaotic time series [J]. Acta Physica Sinica, 2009, 58(9): 5997-6005.
[11]GU Chenjie. A projection-based nonlinear model order reduction approach using quadratic-linear representation of nonlinear systems [J]. IEEE Transactions On
Computer Aided Design of Integrated Circuits and Systems, 2011, 30(9): 1307-1320.
[12]吕金虎, 陆君安, 陈士华. 混沌时间序列分析及其应用 [M]. 武汉: 武汉大学出版社, 2002.
[13]李鹤, 杨周, 张义民, 等. 基于径向基神经网络预测的混沌时间序列嵌入维数估计方法 [J]. 物理学报, 2011, 60(7): 70512.
LI He, YANG Zhou, ZHANG Yimin, et al. Methodology of estimating the embedding dimension in chaos time series based on the prediction performance of radial basis function neural networks [J]. Acta Physica Sinica, 2011, 60(7): 70512.
[14]张学清, 梁军. 风电功率时间序列混沌特性分析及预测模型研究 [J]. 物理学报, 2012, 61(19): 190507.
ZHANG Xueqing, LIANG Jun. Chaotic characteristics analysis and prediction model study on wind power time series [J]. Acta Physica Sinica, 2012, 61(19): 190507.
(编辑 赵炜 杜秀杰)
ANovelVolterraPredictionModelforPowerSystemShort-TermLoadPrediction
HUI Meng,LIU Panzhi
(School of Electronics and Control, Chang’an University, Xi’an 710064, China)
Focusing on short-term load forecasting in power system, a novel Volterra model is proposed. Once determining whether chaotic character exists in the load time series, the load time series is reconstructed following phase space reconstruction theory. Compared with normal Volterra model, the new Volterra model contains more accurate information of system without truncated errors. This Volterra model is used to predict a short-term load and the results show that the error between the predicted load and true load is less than 5%. The predicted short-term load is accurate enough for electric power dispatching, especially for power companies to adjust price.
power system; short-term load; Volterra model
2014-05-05。
惠萌(1981—),男,博士,讲师。
国家自然科学基金资助项目(41101357);中央高校基本科研业务费专项资金资助项目(2013G1321037)。
10.7652/xjtuxb201409005
TM715
:A
:0253-987X(2014)09-0024-06
