磁性液体两相界面演变特性的数值研究
2014-08-08施东晓毕勤成周荣启
施东晓,毕勤成,周荣启
(西安交通大学动力工程多相流国家重点实验室, 710049, 西安)
磁性液体两相界面演变特性的数值研究
施东晓,毕勤成,周荣启
(西安交通大学动力工程多相流国家重点实验室, 710049, 西安)
为了克服VOF,Level Set等方法在磁性液体两相流动研究中存在的不足,采用界面追踪法(VOSET, coupled Volume-of-Fluid and Level Set)捕捉相界面,将磁场力作为源项添加到流体运动的动量方程中,建立了磁性液体流场与磁场耦合的数值方法。推导了麦克斯韦方程的二维理论解并用于验证数值解,两者吻合良好,验证了磁场求解的正确性;同时通过模拟磁性液体液滴的平衡形状验证了本数值方法的准确性;进而分别研究了均匀磁场作用下磁性液体液滴振荡及非磁性气泡在磁性液体中上升的问题。研究结果表明,液滴或气泡均会沿磁场方向拉长,增大磁场强度或磁化率将导致更显著的变形;磁感线在相界面出现弯曲,弯曲方向指向磁导率较大的介质。
磁性液体;两相流;数值模拟;界面追踪法
磁性液体(ferrofluids或magnetic fluids)是含有颗粒直径10nm左右的单磁畴磁性颗粒稳定胶体悬浮液[1]。与磁流变流体在外加强磁场中会发生固化不同,包覆在颗粒表面的活性剂分子使得磁性液体仍可以保持良好的流动性。凭借独特的磁性与流动性,磁性液体在真空密封、扬声器冷却、生物医学工程等领域已有了一定的实际应用[2]。在这些应用中,往往涉及到了带有相界面的磁性液体两相流动。由于外部磁场施加在相界面上麦克斯韦应力的作用,磁性液体的自由表面流动与普通流体存在很大的差异。研究表明,磁性液体液滴或磁性液体中的非磁性气泡均会沿磁场方向拉长[3-4],施加一个非均匀磁场可以控制磁性液体液滴的运动轨迹[5-6],这使得远程非接触操控液滴成为可能。建立准确的数理模型有助于进一步揭示磁场和流场的耦合机制,拓展磁性液体的应用。
气泡或液滴的运动是两相流中的基本问题,目前已有学者针对磁性液体气泡/液滴的行为开展了相关的研究。Korlie等采用VOF方法模拟了气泡在磁性液体中的上升过程[7];Zhu等运用Level Set方法研究了磁性液体液滴在超疏水表面上的非线性变形[8];Liu等采用Particle Level Set方法模拟了微流体流动聚焦结构中磁性液体液滴的生成过程[9]。VOF和Level Set方法因为可以处理带有复杂界面拓扑变化的两相流动问题而被广泛采用,但这两种方法均存在各自的缺点。VOF计算界面曲率及法向不够准确,且求得的界面附近的物性分布是不连续的,将影响表面张力和磁力的计算精度;Level Set则存在质量损失问题,难以模拟尖锐的界面。Particle Level Set虽然能够在一定程度上解决质量损失问题,但该方法执行较为复杂,通用性不强。界面追踪法(VOSET)[10]是近几年刚提出的一种耦合VOF和Level Set方法的新型界面捕捉技术,不仅继承了VOF方法的高质量守恒性,还结合了Level Set函数光滑性好的优点,可以提高界面曲率的计算精度并光顺界面附近突变的物理量。VOSET只需求解流体体积函数的输运方程,而Level Set函数则是通过几何方法确定,极大地简化了计算过程。
本文首次将VOSET方法与磁场力模型相结合,建立了模拟均匀磁场中磁性液体不可压缩两相流动的二维数值模型。控制方程包括静磁场非导电流体的麦克斯韦方程,以及耦合表面张力和磁力的动量方程。为了验证麦克斯韦方程求解的准确性,首先推导了适用于二维坐标系下的磁势拉普拉斯方程的理论解,并将数值解与其进行对比。同时通过模拟磁性液体液滴的平衡形状验证了本数值方法的正确性。随后根据本文建立的数值模型分别研究了均匀磁场作用下磁性液体液滴振荡及气泡在磁性液体中上升的问题。
1 数学模型与数值方法
1.1 控制方程
假设纳米磁性颗粒在基液中为均匀的单分散状态,且相互之间不发生作用,在对磁性液体宏观行为的研究中,可以将磁性液体当作性质单一的均匀流体进行处理[7,9]。磁场对磁性液体界面变形的影响来源于作用在相界面上的麦克斯韦应力,该应力可以简化为界面上的法向应力。考虑不可压缩两相流体的流动,表面张力和磁力存在于相界面,连续方程及动量方程可描述为
(1)

(2)
式中:u、ρ、η和p分别为流体的速度、密度、黏度和压力;Fσ为表面张力。方程(2)右边的最后一项为磁力项,采用与表面张力相同的处理方式,将磁力以源项的形式添加到动量方程中。麦克斯韦应力张量τm有如下形式

(3)
式中:μ为磁导率;H为外加磁场;I为单位张量。
1.2 界面追踪法
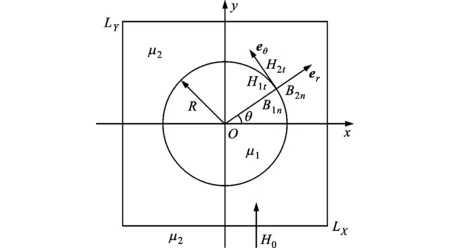
VOSET采用VOF方法捕捉相界面,保持了两相间的质量守恒;构造界面附近的Level Set符号距离函数φ用来计算界面曲率、法向和光滑不连续的物性,克服了VOF方法计算曲率不精确和光滑物性差的缺点。
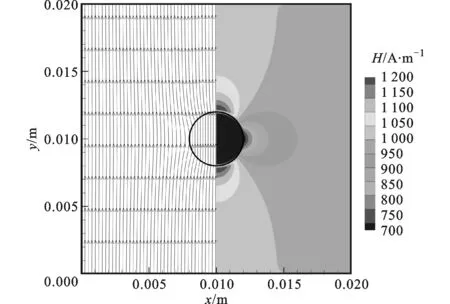
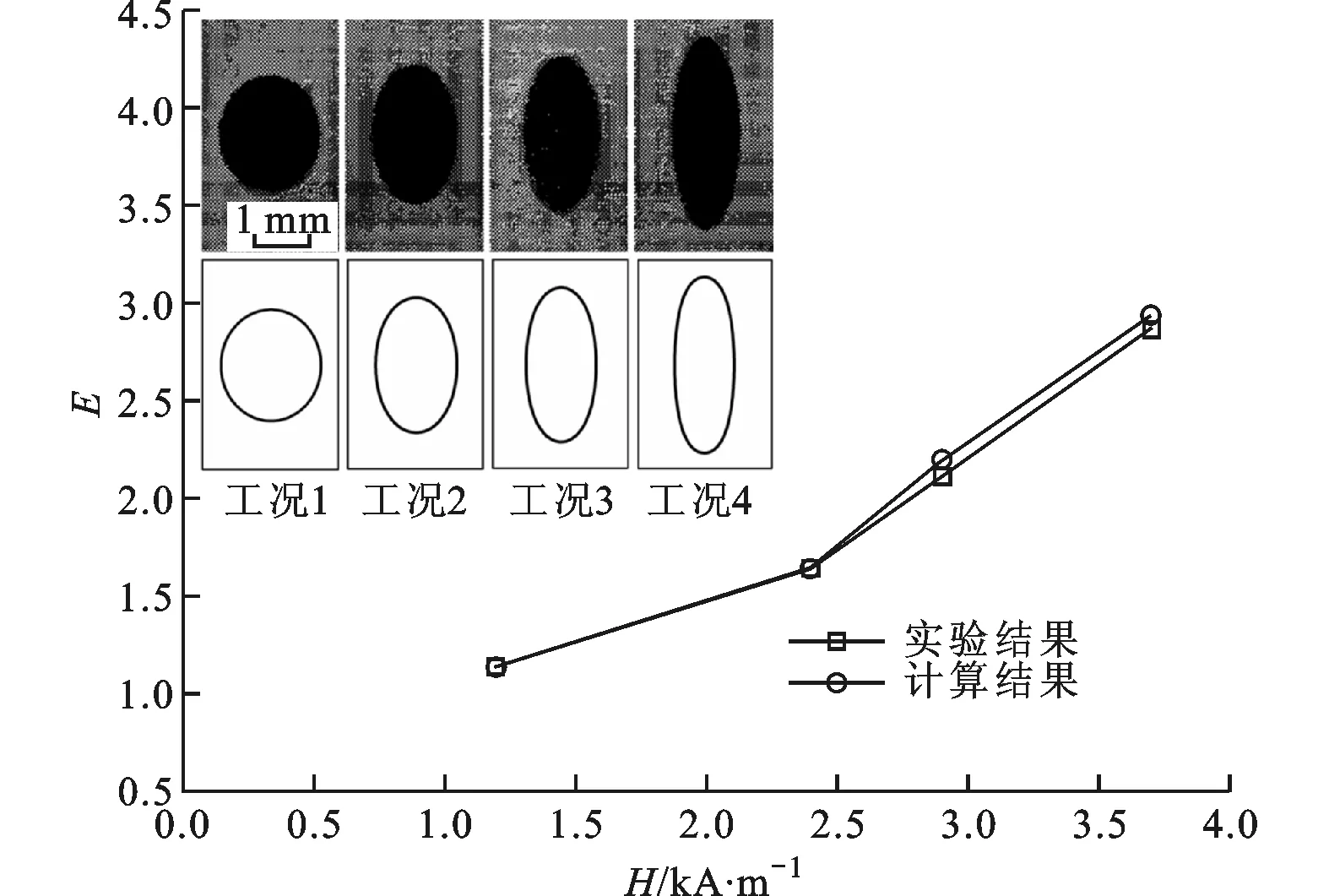
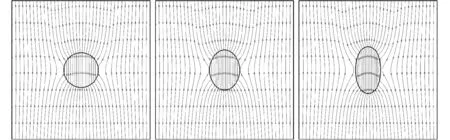
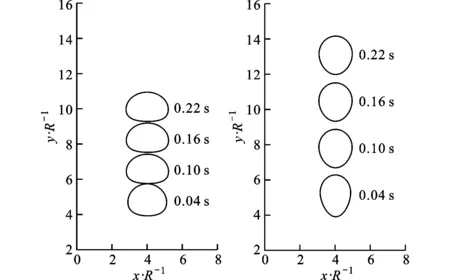
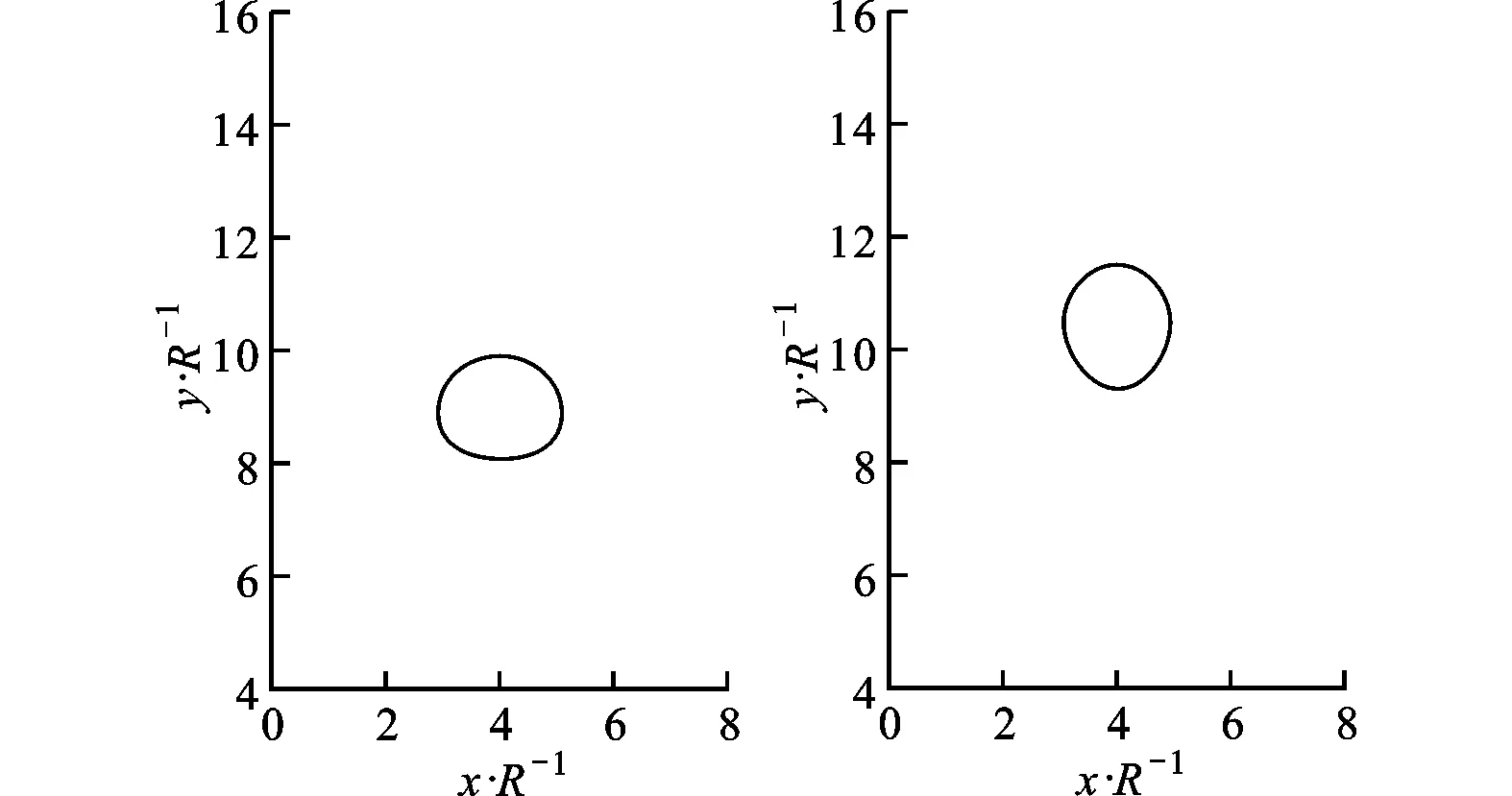
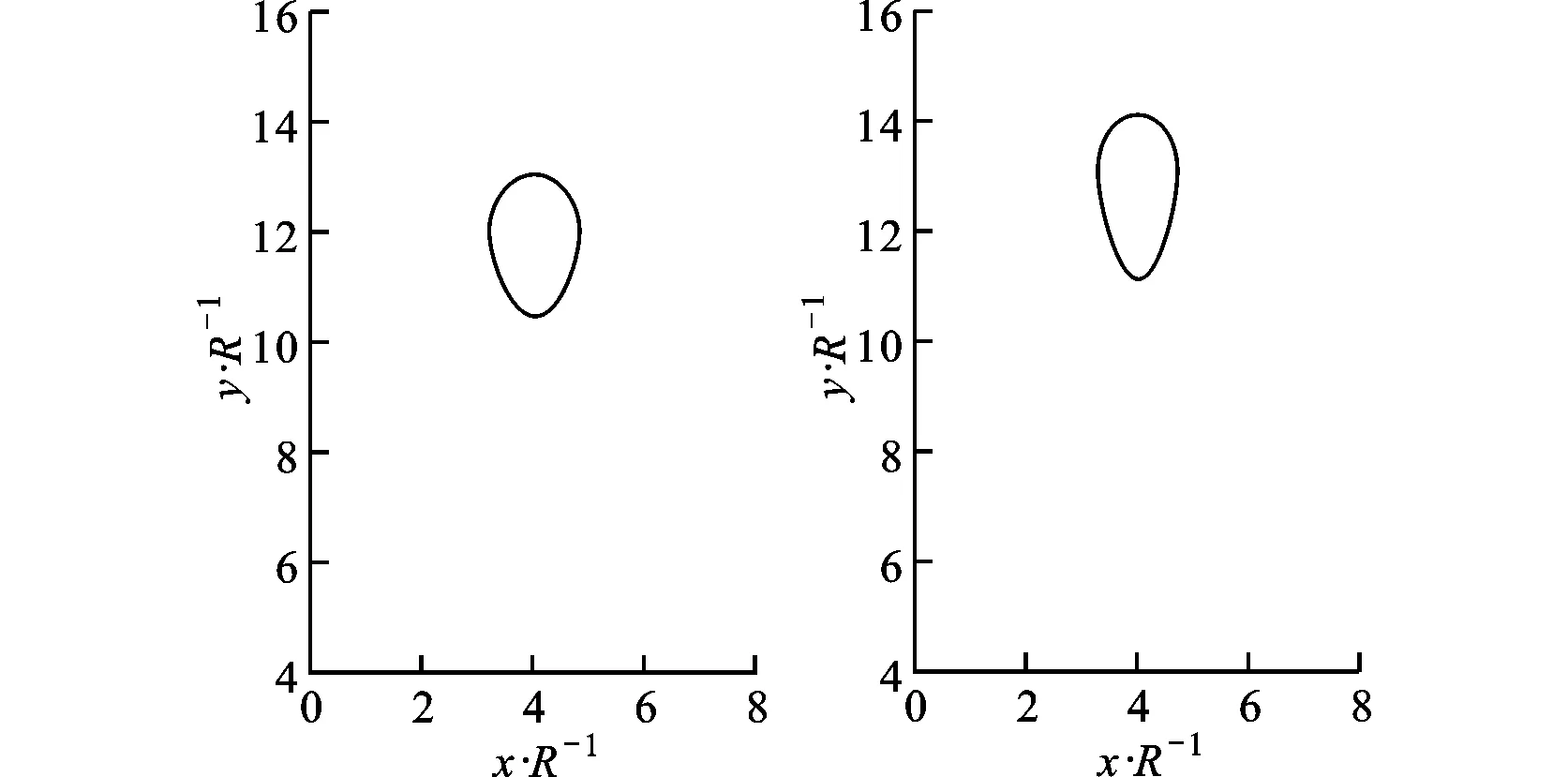
在VOF方法中,采用流体体积函数C表示计算单元中流体占据单元空间的体积分数,定义C=0表示网格内全为连续相,C=1表示网格内全为离散相,0 (4) 方程(4)的求解和相界面的重构采用了Youngs的PLIC算法[11]。 根据求得的流体体积函数,通过迭代几何计算方法求出界面两侧各3倍网格宽度区域内的Level Set函数,步骤如下:①在整个计算区域内为Level Set函数赋初值;②标识相界面附近的计算单元;③计算标识区域内单元(i,j)到界面的最短距离d,根据下式确定符号距离函数的值 (5) ④用求得的Level Set函数φ重新求界面法向n=φ/|φ|,根据新的法向再次构造界面,重复步骤③、④,详细的计算过程参考文献[10]。 采用Level Set函数来光滑密度、黏度和磁导率 ρ(φ)=ρd+(ρc-ρd)Hε(φ) (6) η(φ)=ηd+(ηc-ηd)Hε(φ) (7) μ(φ)=μd+(μc-μd)Hε(φ) (8) 式中:下标d和c分别表示离散相和连续相;Hε(φ)为光滑Heaviside函数[12],其表达式为 (9) 本文取系数ε=1.5Δ,其中Δ为网格宽度。 表面张力由连续表面力(CSF)模型给出,写成Level Set函数形式[12]有 Fσ=-σκ(φ)Hε(φ) (10) 式中:σ为表面张力系数;κ为界面曲率,由下式得出 κ(φ)=· (11) 1.3 磁场力模型 一般认为磁性液体为非导电流体,且流体中不存在位移电流,描述磁场的麦克斯韦(Maxwell)方程组则可简化为 (12) 施加外磁场时,磁性液体内部的磁性颗粒磁矩沿外磁场方向排列,使得磁性液体对外显磁性,定义单位体积内颗粒磁矩的矢量和为磁化强度M。磁感应强度B、磁场强度H以及磁化强度M之间满足本构关系 B=μ0(H+M) (13) (14) 引入标量磁势ψ,定义H=-ψ,将方程(12)的求解转化为求解关于磁势的拉普拉斯方程·(μψ)=0 (15) 在外加磁场作用下,流体中产生的磁界面力可以由麦克斯韦应力张量给出Fm=·τm,采用与表面张力相同的处理方式,将表面力转化为体积力,那么单位体积磁力的表达式为[1] Fm=-μ0H,TdH+μ0MH (16) 磁化强度M(μ,H,T)为外磁场和温度的函数,将式(16)展开得 Fm=-μ0MdH+μ0υH,TdH+ μ0MH (17) 式(17)右边第一项表示流体-磁压力项,即 (18) (19) 此外,式(17)右边第二项为磁致伸缩压力项,即 (20) 将M=(μ-μ0)H/μ0及比容υ=1/ρ代入上式,得ps=0。 基于以上分析,磁力公式(16)最终简化为 (21) 1.4 数值方法 在二维均匀直角网格上采用有限容积法离散控制方程,磁势方程(15)的离散采用二阶精度的中心差分法,方程(1)和(2)的求解在交错网格上执行,压力与速度的耦合采用SIMPLER算法。一个时间步长内的计算过程如下:①由t时刻的流体体积函数Cn根据VOSET方法求出Level Set函数φn;②求解方程(15)获得磁场分布Hn;③ 由求得的φn和Hn计算表面张力和磁力,代入方程(2),求出t+1时刻的速度场un+1;④根据新的速度场un+1,采用Youngs的PLIC界面重构技术构造下一时刻的界面Cn+1。 2.1Maxwell方程求解与验证 导磁圆球在均匀磁场中的磁势方程存在理论解[1],可用于验证Maxwell方程的数值解。球坐标系下磁势理论解表征的是三维磁场分布,针对二维情况,圆球模型不再适用,应采用无限长圆柱体模型,如图1所示,计算区域为LX×LY,中心圆柱体半径为R,内部磁导率为μ1,外部磁导率为μ2,施加竖直向上的均匀磁场H0。 图1 计算模型示意图 (22) 式中:r为空间中任意一点到圆心的距离。方程(22)的解为 (23) 根据磁势定义可求得磁场分布 (24) Maxwell方程的边界条件[1]为 n·(B1-B2)=0 n×(H1-H2)=0 (25) 式中:n为界面法向;B1、B2、H1和H2分别表示界面两侧的磁感应强度和磁场强度矢量。由式(25)可知B场在界面法向连续,即B1n=B2n;H场在界面切向连续,即H1t=H2t。当r→∞时,H=H0j(j=ersinθ+eθcosθ),因此E=-H0。根据界面边界条件,求得系数A和D (26) 采用有限容积法离散磁势方程,对于二维直角坐标,磁势方程(15)可写成 (27) 选取计算参数:LX=0.02m,LY=0.02m,R=0.002m,μ2=μ0,μ1=2μ0,H0=1 kA·m-1,网格200×200。图2对比了y轴上的磁场值,理论解求得圆内磁场值为0.667 kA·m-1,数值解为0.662kA·m-1,两者基本吻合,表明Maxwell方程求解是正确的。 图2 沿y轴(x=0.01 m)的磁场强度 图3给出了圆柱周围磁场及磁感线的分布,圆柱内部磁场分布均匀,磁感线与外磁场同向;圆柱内外磁导率的突变导致磁感线在界面附近发生扭曲,而在远离圆柱的区域又恢复为均匀。 图3 磁场及磁感线分布 2.2 磁性液体液滴的平衡形状 为验证本文建立的模型及方法,首先计算了初始静止的磁性液体液滴在均匀磁场中的平衡形状问题,并将计算结果与Flament等人的实验结果[13]进行对比。半径R=0.001 m的液滴位于8R×8R的区域中心,磁化率为2.2,表面张力为3.07 mN·m-1,不计重力,壁面采用无滑移速度边界条件,计算网格取128×128。图4给出了不同大小磁场作用下液滴的平衡形状及高宽比与实验结果的对比。定义液滴在平行和垂直于磁场方向上的直径的比值E来表征液滴的变形程度[14]。图4中工况1~4所对应的磁场大小分别为1.2、2.4、2.9及3.7 kA·m-1。可以看出,计算结果与实验结果吻合较好,证明本文的数值算法可有效地计算磁性液体的两相流动问题。 图4 计算结果与实验结果[13]的对比 2.3 磁性液体液滴振荡 下面模拟磁性液体液滴在均匀磁场中的振荡过程。计算区域为0.08 m×0.08 m,半径为0.01 m的圆形液滴位于区域中心,液滴及周围空气的物性参数为ρd=103kg·m-3,ρc=1 kg·m-3,ηd=10-3Pa·s,ηc=10-5Pa·s,μd=10μ0,μc=μ0,σ=0.1 N·m-1。外加竖直向上的均匀磁场H0=2kA·m-1,不考虑重力,四周设为无滑移固壁,计算网格取112×112。 施加磁场后,麦克斯韦应力在液滴沿磁场方向的两极取最大[7],为保持法向应力平衡,液滴沿磁场方向拉伸成扁长形状,而表面张力阻碍了液滴的进一步拉伸,因此在磁力和表面张力的共同作用下液滴沿竖直方向振荡变形,如图5a~5f所示。图5g~5i为对应于图5a~5c时刻的磁感线分布,可以看出磁感线随液滴形状的变化而改变,且磁感线朝着液滴方向弯曲,这是由于液滴磁导率大于空气磁导率。 (a)0s (b)0.07 s (c)0.16 s (d)0.24s (e)0.30s (f)0.37 s (g)0s (h)0.07 s (i)0.16 s 2.4 磁性液体中气泡上升 考虑8R×16R的计算区域,半径R=0.004m的气泡初始位于(4R,4R),均匀磁场竖直向上,网格取112×224。采用Eo数和Mo数描述气泡的运动特性 (28) (a)无磁场 (b)竖直磁场(Bom=4) 图7为0.16 s时不同磁场中的气泡形状及磁感线分布,Bom=2时磁场较弱,气泡仍为扁平的椭圆形;随着磁场强度的增大,气泡逐渐沿磁场方向变形,且磁场越强变形越明显。磁感线在气泡附近发生扭曲,并背离气泡方向弯曲,与磁性液体液滴的情况相反。 (a)Bom=2 (b)Bom=4 (c)Bom=6 (d)Bom=8 另外,由磁力公式(21)可知,磁力的大小与磁化率成正比,因此气泡的运动行为还受磁化率的影响。图8展示了相同磁场作用下不同磁化率时的气泡形状(Bom=4,t=0.16 s),可以看出气泡的变形程度随着磁化率的增加而增大。 (a=1 (b=2 (c=3 (d=4 图9给出了气泡的高宽比、最终速度与Bom及磁化率的关系。由于增大磁场强度(Bom)或磁化率均会增大磁力,从而促进了气泡沿磁场方向上的变形。气泡的高宽比越大,受到的阻力越小,上升得越快,因此气泡的形状影响着气泡的上升速度。 (a)气泡的高宽比及速度与Bom的关系 (b)气泡的高宽比及速度的关系 本文对磁场力模型进行了详细推导,采用与表面张力相同的处理方法,给出了磁力的最终表达式,并作为源项添加到动量方程中,结合VOSET方法,建立了模拟磁性液体不可压缩两相流动的二维数值模型。推导了Maxwell方程的二维理论解,并分别计算了均匀磁场中磁性液体液滴振荡与气泡在磁性液体中上升的问题,得出以下结论。 (1)Maxwell方程的数值解与推导的理论解吻合较好,表明本数值方法求解Maxwell方程的正确性。 (2)麦克斯韦应力在磁性液体液滴沿磁场方向的两极取最大,为保持法向应力平衡,液滴被拉长为扁长的形状,而表面张力阻碍了液滴的进一步拉伸,液滴最终在磁力和表面张力的作用下振荡变形。 (3)磁性液体中的非磁性气泡在磁场作用下克服表面张力沿磁场方向拉伸变形,增大磁场强度或磁导率均会增大气泡的高宽比,减小了气泡在运动方向上的阻力,提高了上升速度。 (4)磁感线随着液滴或气泡形状的变化而变化,并在界面附近(磁导率突变的位置)发生扭曲,弯曲方向指向磁导率较大的介质。 (5)本文建立的磁性液体流场与磁场耦合的数值方法,可以为带有相界面的磁性液体流动研究提供理论基础。 [1] ROSENSWEIG R E. Ferrohydrodynamics [M]. Cambridge, UK: Cambridge University Press, 1985. [2] RINALDI C, CHAVES A, ELBORAI S, et al. Magnetic fluid rheology and flows [J]. Current Opinion in Colloid & Interface Science, 2005, 10(3/4): 141-157. [3] ARKHIPENKO V I, BARKOV Y D, BASHTOVOI V G. Shape of a drop of magnetized fluid in a homogeneous magnetic field [J]. Magnitnaia Gidrodinamika, 1979, 14: 131-134. [4] ISHIMOTO J, OKUBO M, KAMIYAMA S, et al. Bubble behavior in magnetic fluid under a nonuniform magnetic field [J]. JSME International Journal: Series B Fluids and Thermal Engineering, 1995, 38(3): 382-387. [5] NGUYEN N T, NG K M, HUANG X. Manipulation of ferrofluid droplets using planar coils [J]. Applied Physics Letters, 2006, 89(5): 052509. [6] PROBST R, LIN J, KOMAEE A, et al. Planar steering of a single ferrofluid drop by optimal minimum power dynamic feedback control of four electromagnets at a distance [J]. Journal of Magnetism and Magnetic Materials, 2010, 323(7): 885-896. [7] KORLIE M S, MUKHERJEE A, NITA B G, et al. Modeling bubbles and droplets in magnetic fluids [J]. Journal of Physics: Condensed Matter, 2008, 20: 204143. [8] ZHU G-P, NGUYEN N T, RAMANUJAN R V, et al. Nonlinear deformation of a ferrofluid droplet in a uniform magnetic field [J]. Langmuir, 2011, 27(24): 14834-14841. [9] LIU J, YAP Y F, NGUYEN N T. Numerical study of the formation process of ferrofluid droplets [J]. Physics of Fluids, 2011, 23: 072008. [10]SUN D L, TAO W Q. A coupled volume-of-fluid and level set (VOSET) method for computing incompressible two-phase flows [J]. International Journal of Heat and Mass Transfer, 2010, 53(4): 645-655. [11]YOUNGS D L. Time-dependent multi-material flow with large fluid distortion [M]∥MORTON K W, BIANES M J. Numerical Methods for Fluid Dynamics. New York, USA: Academic Press, 1982: 273-285. [12]SUSSMAN M, FATEMI E, SMEREKA P, et al. An improved level set method for incompressible two-phase flows [J]. Computers & Fluids, 1998, 27(5/6): 663-680. [13]FLAMENT C, LACIS S, BACRI J C, et al. Measurements of ferrofluid surface tension in confined geometry [J]. Physical Review: E, 1996, 53: 4801. [14]刘艳艳, 李彦鹏, 朱婷婷. 表面活性剂对中尺度气泡形状及速度的调控研究 [J]. 西安交通大学学报, 2011, 45(10): 93-97. LIU Yanyan, LI Yanpeng, ZHU Tingting. Study on modulating shape and velocity of meso-scale bubble using surfactants [J]. Journal of Xi’an Jiaotong University, 2011, 45(10): 93-97. (编辑 荆树蓉) NumericalInvestigationontheEvolutionCharacteristicsofTwo-PhaseInterfaceinFerrofluids SHI Dongxiao,BI Qincheng,ZHOU Rongqi (State Key Laboratory of Multiphase Flow in Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China) To overcome the disadvantages of VOF and Level Set methods in the research of ferrofluid two-phase flows, a numerical method coupling the flow field with magnetic field of ferrofluids was developed, where the evolution of interface was captured by the VOSET (coupled Volume-of-Fluid and Level Set) method, and the magnetic force was added into the momentum equation as a source term. To verify the accuracy of solving magnetic fields, a 2D analytical solution of Maxwell equations was derived and used to validate the numerical solution. The numerical results were in good agreement with the theoretical values. Then, the equilibrium shape of a ferrofluid droplet was simulated which verified the validity of our numerical method. Based on the proposed method, the droplet oscillation and rising bubble problems in the presence of magnetic fields were numerically investigated. The results showed that both the droplet and bubble were stretched in the direction of magnetic field, and the increase in either magnetic field strength or magnetic susceptibility would lead to a more significant deformation. Note that the magnetic field lines were distorted in the vicinity of interface with the bending direction pointing to the medium with a higher susceptibility. ferrofluids; two-phase flow; numerical simulation; interface tracking method 2014-02-04。 施东晓(1987—),男,博士生;毕勤成(通信作者),男,教授,博士生导师。 国家自然科学基金资助项目(11072189);国家“863计划”资助项目(2008AA05Z417)。 时间:2014-06-13 10.7652/xjtuxb201409021 O359.1 :A :0253-987X(2014)09-0123-07 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140613.1457.005.html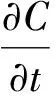
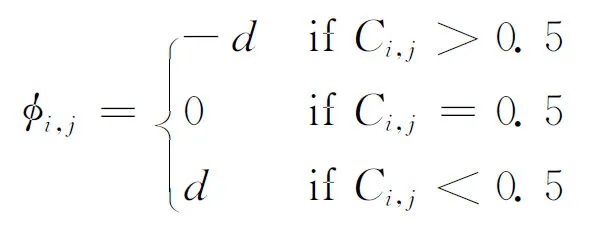


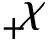

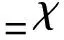
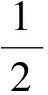
2 结果与分析
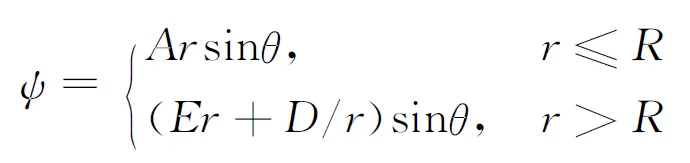

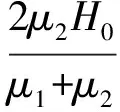





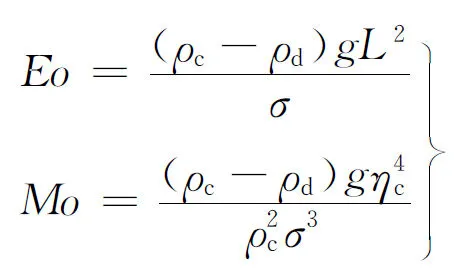
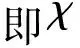


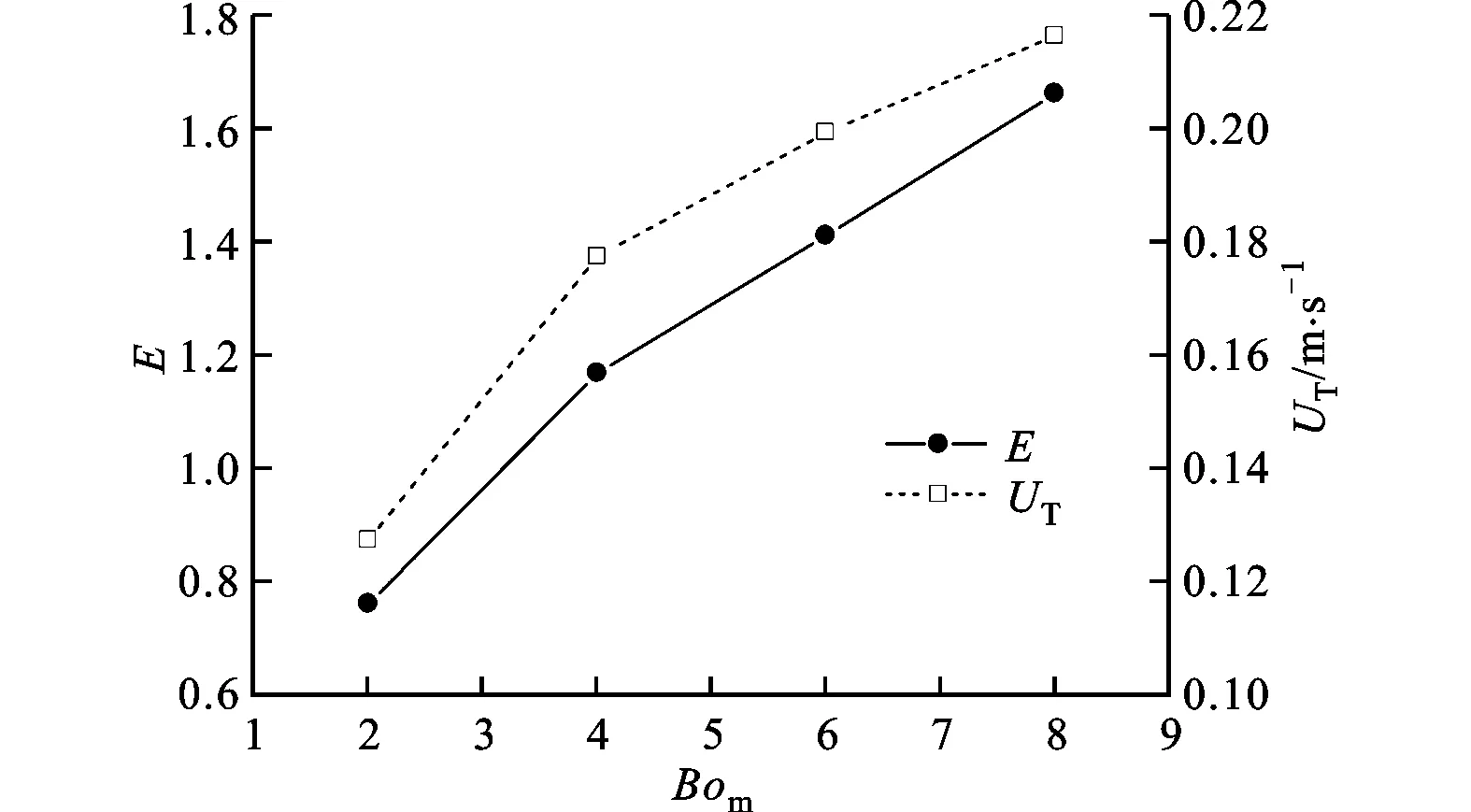
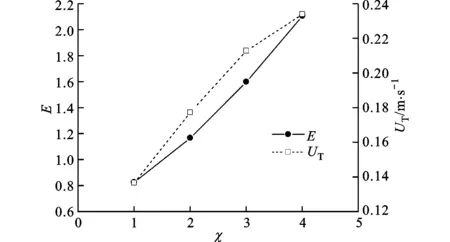
3 结 论
