空气源跨临界CO2热泵最优排气压力的理论和实验

宋昱龙,唐学平,王守国,杨东方,曹锋

(1.西安交通大学能源与动力工程学院, 710049, 西安; 2.江苏白雪电器股份有限公司, 215500, 江苏常熟)

空气源跨临界CO2热泵最优排气压力的理论和实验

宋昱龙1,唐学平2,王守国1,杨东方1,曹锋1

(1.西安交通大学能源与动力工程学院, 710049, 西安; 2.江苏白雪电器股份有限公司, 215500, 江苏常熟)

为了研究空气源跨临界CO2热泵系统中影响最优排气压力的主要因素,以跨临界CO2热泵机组为平台,在焓差室中进行了制热性能测试。结果表明,系统的蒸发压力和气冷器出口温度随排气压力的上升而下降,过热度随排气压力的上升而上升,制热量与制热能效比随排气压力的上升先上升后下降,且存在一个最优值。综合实验数据可以看出,系统的最优排气压力随着环境温度、进水温度、出水温度的下降而降低。在进水温度(环境水温)没有剧烈变动的条件下,通过数据拟合的方法创新性地提出了以环境温度及出水温度为自变量的预测最优排气压力的实验关联式。实验对比证明,系统运行在预测最优排气压力时,制热能效比与实验最优值的偏差小于1.3%,说明以环境温度及出水温度为自变量的预测最优排气压力的方法是值得同行参考的一种有效方法。

跨临界CO2热泵;最优排气压力;关联式

在人们对环境问题日益关注的今天,CO2作为无毒、不可燃且臭氧衰减指数(ODP)为0及温室效应指数(GWP)极低的天然制冷剂受到了广泛的推崇[1]。在CO2热泵热水器的研究中,核心内容是最优排气压力(简称最优排压)。Lorentzen指出,CO2在气体冷却器(简称气冷器)出口的温度是决定最优排压的关键因素[2];Kauf提出了最优排压与气冷器出口温度或环境温度之间的计算关联式[3];Liao研究了压缩机绝热效率对最优排压的影响[4];Sarkar从理论角度上分析了最优排压存在的原因,并以气冷器出口温度和蒸发温度为变量提出了最优排压的预测关联式[5];Chen等将气冷器出口温度与环境温度对应起来,从而使关联式中的变量简化为单一变量[6];Gecchinato等对最优排压问题做了理论和实验探究[7-8]。以上研究中,选择蒸发温度及气冷器出口温度作为最优排压的主要影响因子的合理性值得商榷。

本文从理论的角度分析了跨临界CO2热泵中最优排压存在的原因,阐明了工作在最优排压附近的系统性能及影响因素,根据环境温度及出水温度(主要影响因素)建立了最优排压的实验关联式。

1 空气源跨临界CO2热泵系统的分析

1.1跨临界CO2热泵循环系统的组成及特性

CO2亚临界循环、超临界循环和跨临界循环如图1所示,图中点1～4分别代表吸气点、排气点、气冷器出口和蒸发器入口;跨临界CO2制冷系统如图2所示。CO2在气冷器中的换热过程不同于一般的显热换热,故被定义为类显热换热。

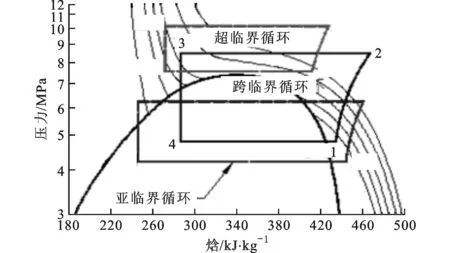
图1 3种CO2制冷循环的压焓

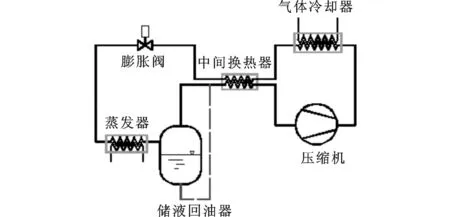
图2 跨临界CO2制冷系统

1.2跨临界CO2热泵最优排压的理论分析

忽略高压侧制冷剂压力损失,高压侧CO2放热过程中单位温度变化造成的焓差变化是非均等的,这种在超临界区内的物性决定了跨临界CO2热泵系统将存在一个最优排压。

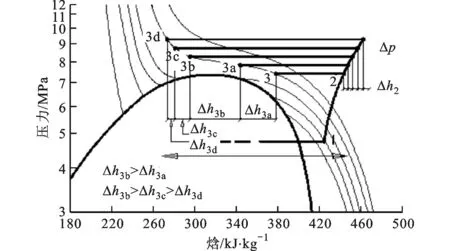
图3 排压对系统制热量和COP的影响

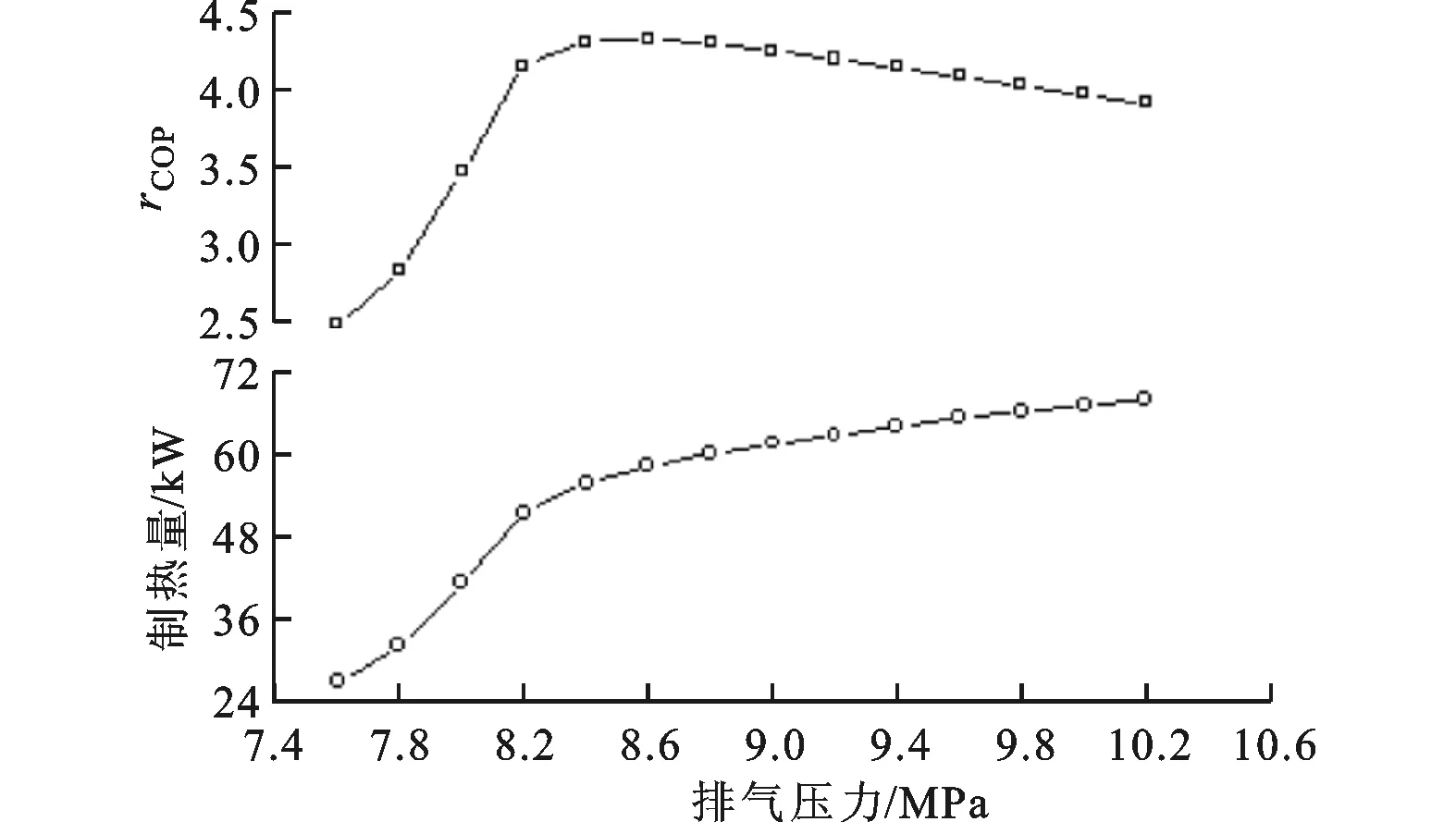
图4 系统制热量和COP随排压变化的情况

图5 气冷器出口温度对COP的影响

如图3,在临界点附近及以上的区域,等温线比较平缓,距离临界点越远,等温线越陡峭。点2到点3(3a,3b,3c,3d)为5种可能达到的排压值,当等熵效率、容积效率及蒸发温度一定时,系统中压缩机功率随排压的升高基本上是线性增加的,增量由Δp表示,气冷器进、出口焓差(制热量)增量随排压的升高先增大后减小,由Δh表示,因此系统制热能效比(COP,符号为rCOP)也是呈先增大后减小的趋势。蒸发温度为10℃、气冷器出口温度为35℃时,系统制热量和COP随排压的变化如图4所示。从图4可以看出,随着排压的升高,系统COP呈现出先升高后缓慢降低的过程,说明最优排压存在并且极大地影响着系统COP。气冷器出口温度对系统COP的影响如图5所示。从图5可以看出,每一个确定的气冷器出口温度都对应着一个最优排压,气冷器出口温度越低,最优排压就越低。当排压小于最优值时,COP随排压的波动较大;当排压大于最优值时,COP较稳定。所以,实际中排压应维持在最优排压或稍大于最优排压的范围内,以避免COP出现大的波动[9]。

2 排压对热泵系统性能的影响

本文实验均在高温热泵专用焓差室中进行,该实验室分为环境室、空气和水调节系统、电控系统及测量系统4部分。环境室通过调节温湿度可模拟不同的环境工况;空气与水循环系统分别参与气冷器与蒸发器换热;电控系统主要控制机组的正常运行与监测,并通过改变膨胀阀开度来调节高压侧压力;测量系统采用水量热计法测量水侧换热量和各个关键点的压力、温度等。由此,可计算系统COP,得到相关实验数据。实验样机三维模拟图如图6所示。

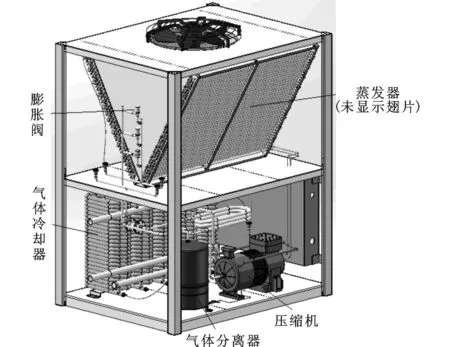
图6 样机三维模拟图

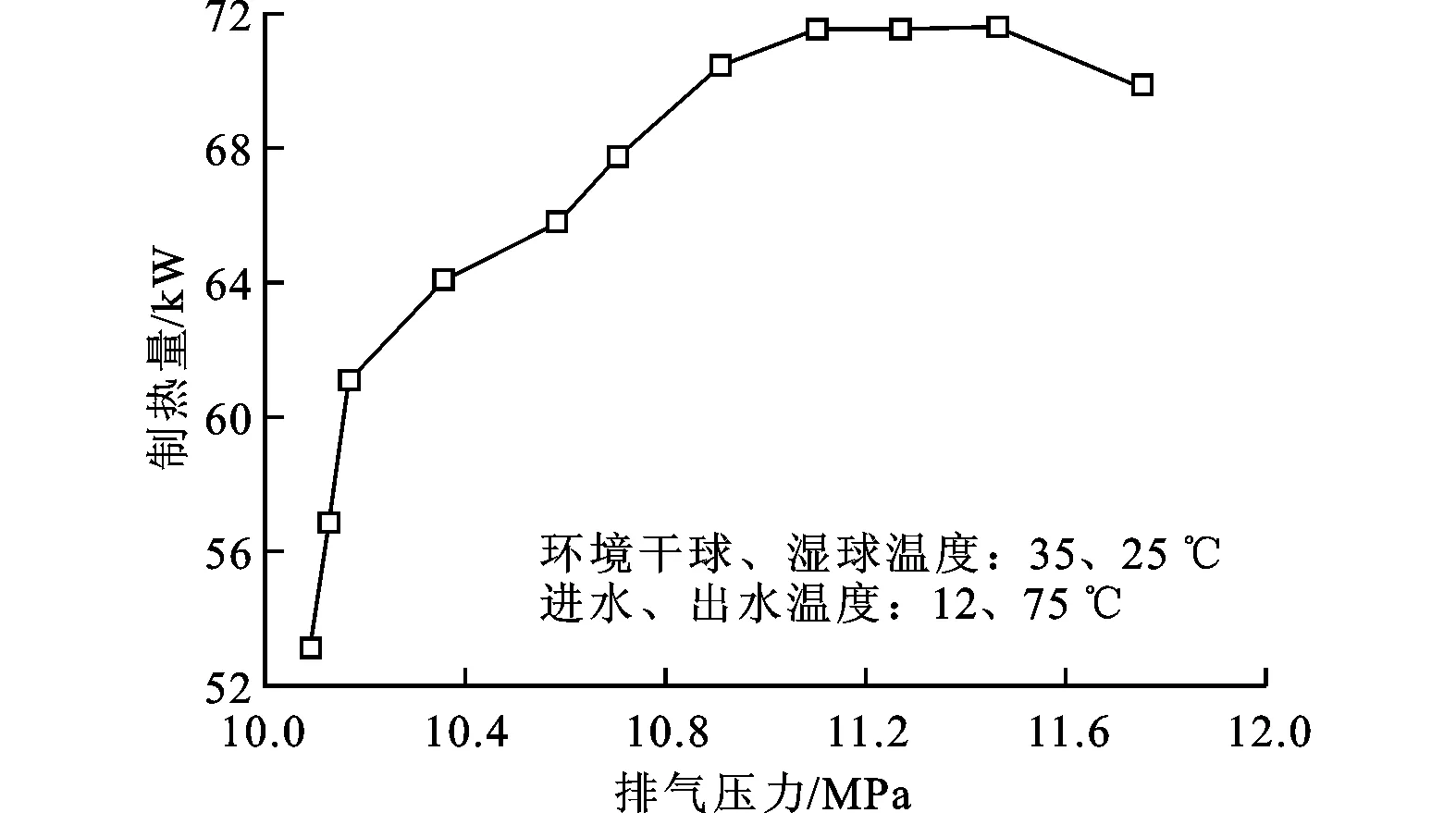
图7 系统制热量随排压的变化

2.1 排压对制热量的影响

当环境及进出水的温度确定时,系统制热量随排压的变化如图7所示。从图7可以看出,随着排压的升高,系统制热量呈现出先升高后平缓下降的过程,排压为(11.3±0.05) MPa时,制热量达到最大。不同的环境和进出水温度下,随着排压的升高,制热量均呈现出类似的变化过程。

气冷器内焓差随着排压的升高而增加,气冷器出口温度随之降低,制冷剂的焓差增量随排压的升高呈现出先增后减的趋势。由于气冷器出口温度受限于进水温度,不能够无限减小,所以高压侧焓差将限制在一定的范围之内。另外,随着排压的升高,压缩比增大,系统质量流量减小,系统制热量呈现出先增后平缓下降的过程(见图7)。

需指出,跨临界CO2热泵的压缩比要远小于常规制冷剂在相同工况下的压缩比,而由压缩比升高造成质量流量降低也应小于常规制冷剂随排压的变化。在确定的环境及进出水温度工况下,压缩比随排压的变化如图8所示。

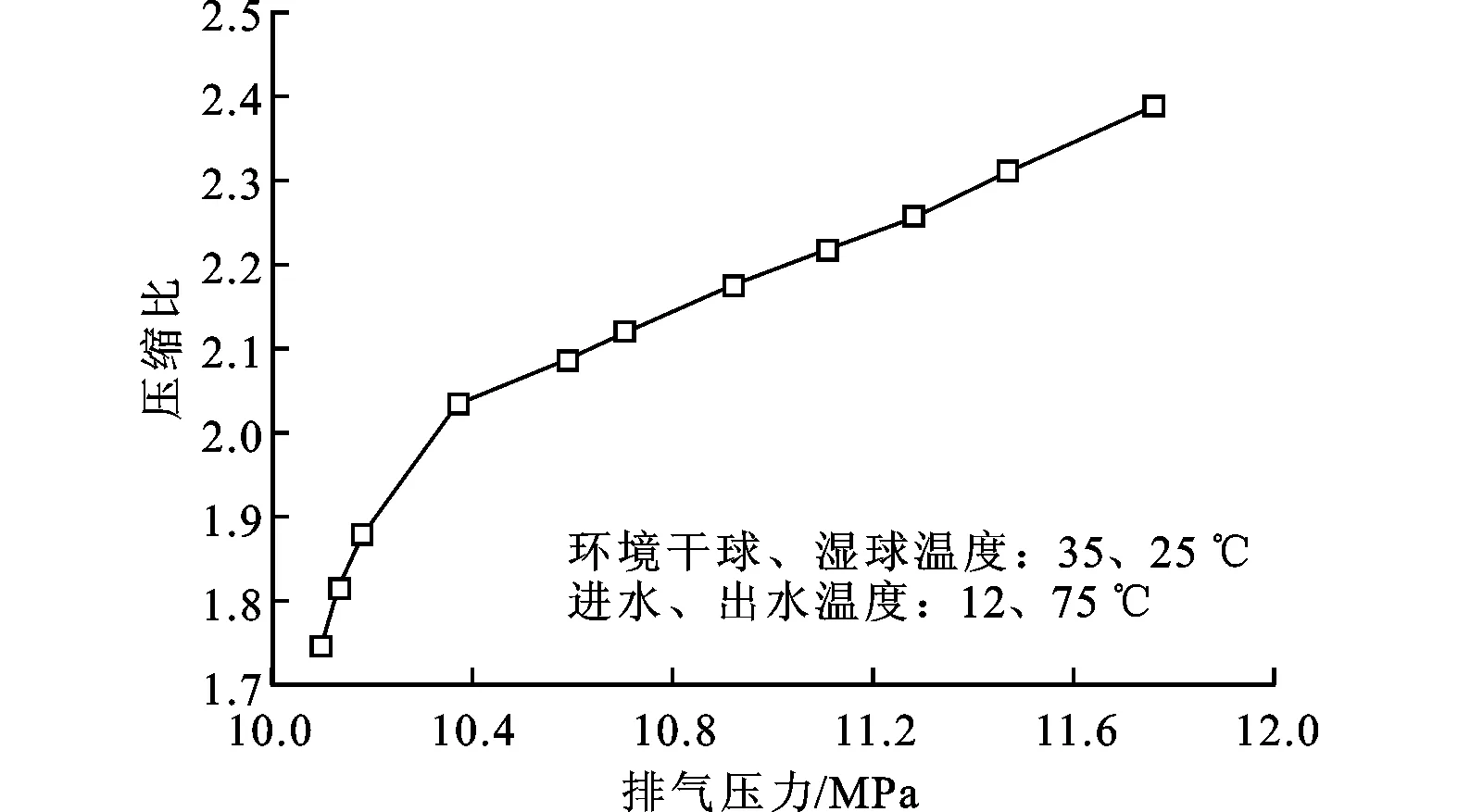
图8 压缩比随排压的变化

2.2 排压对系统COP的影响

环境及进水温度确定后,不同出水温度时系统COP随排压的变化如图9所示。从图9可以看出,随着排压的变化,每一出水温度下系统COP总是呈现出先增后减的趋势,表明实际中存在最优排压,这印证了理论分析结果。

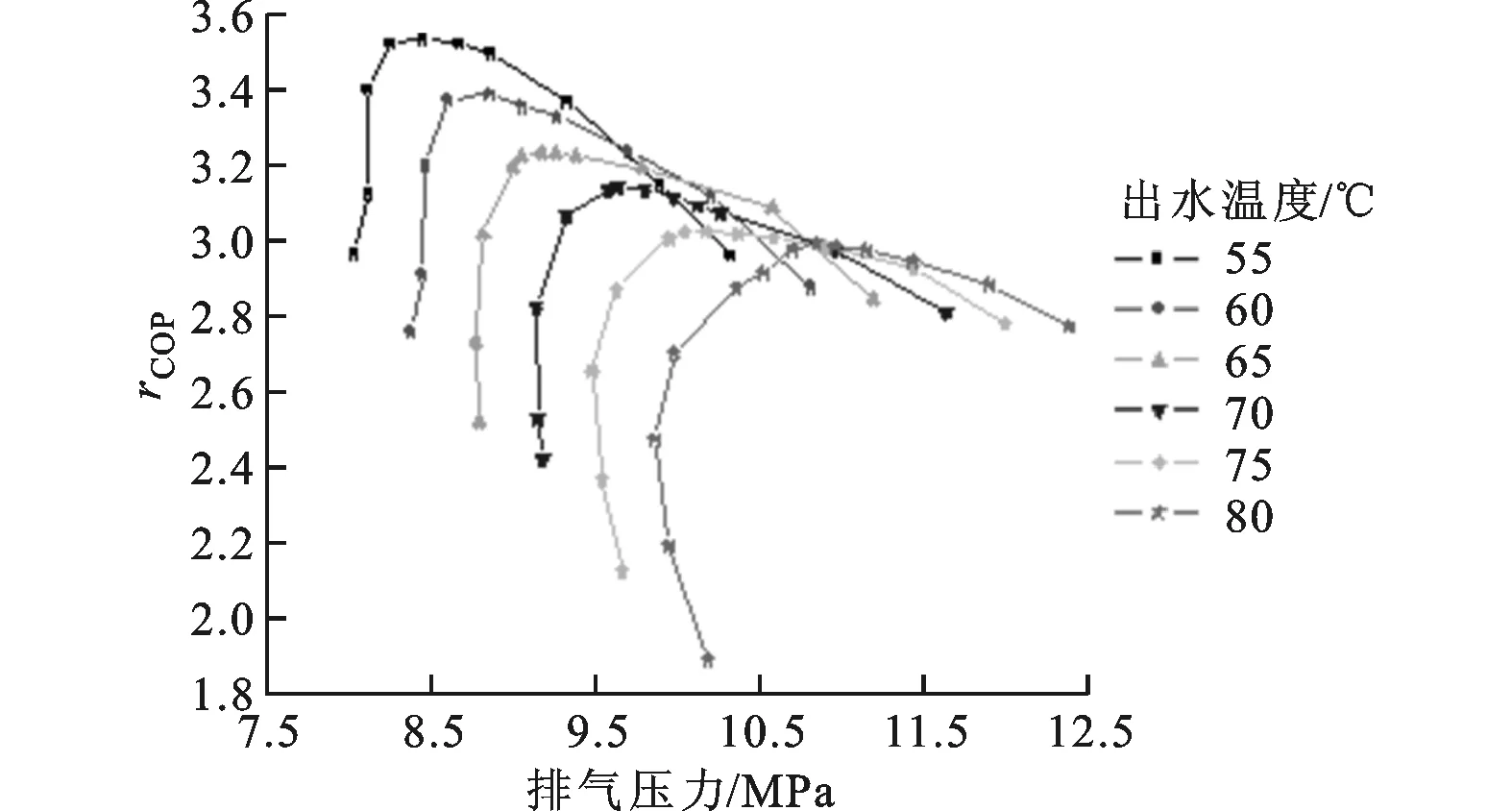
(a)环境温度为15℃

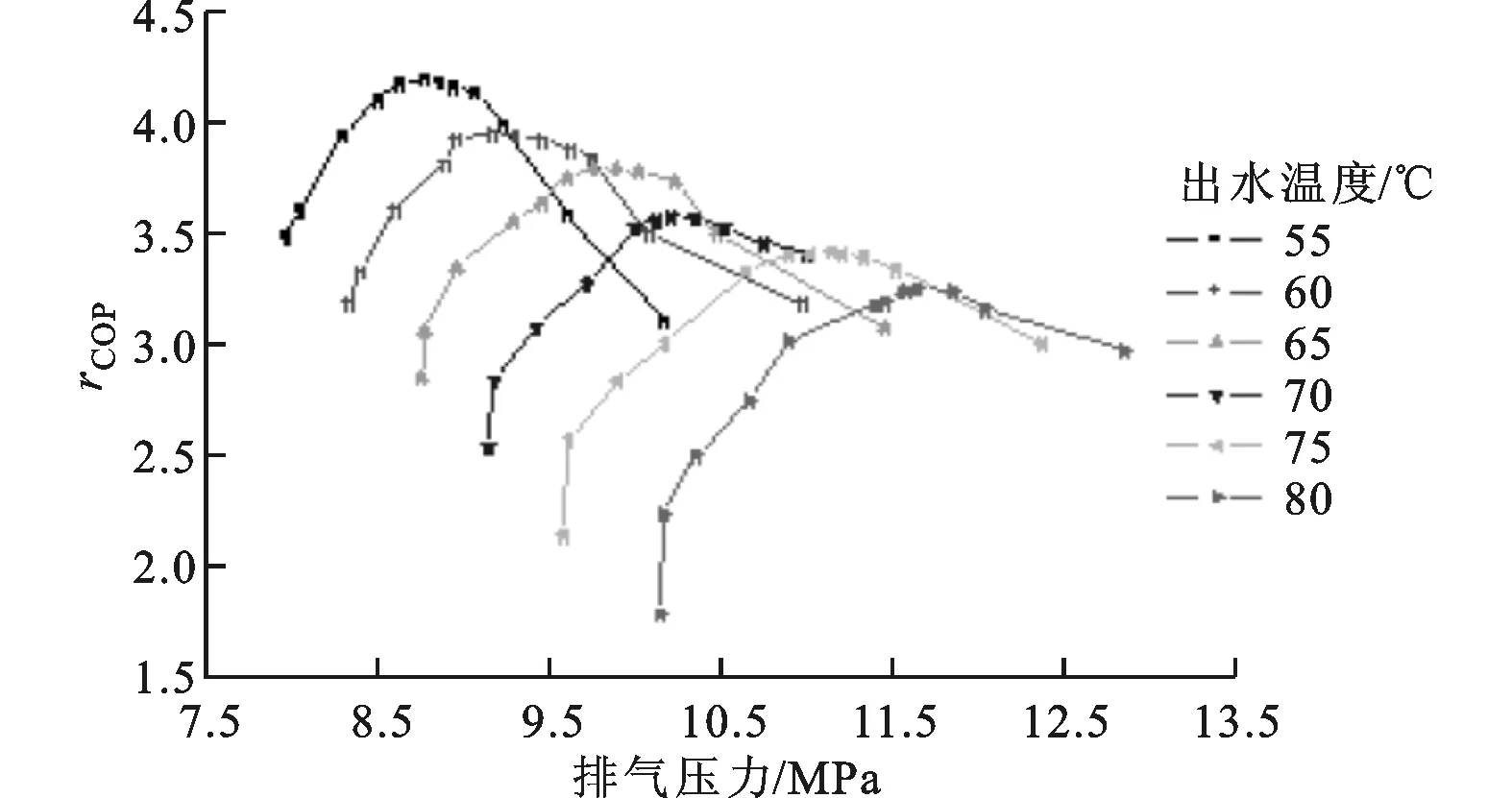
(b)环境温度为25℃

2.3 排压对蒸发压力的影响

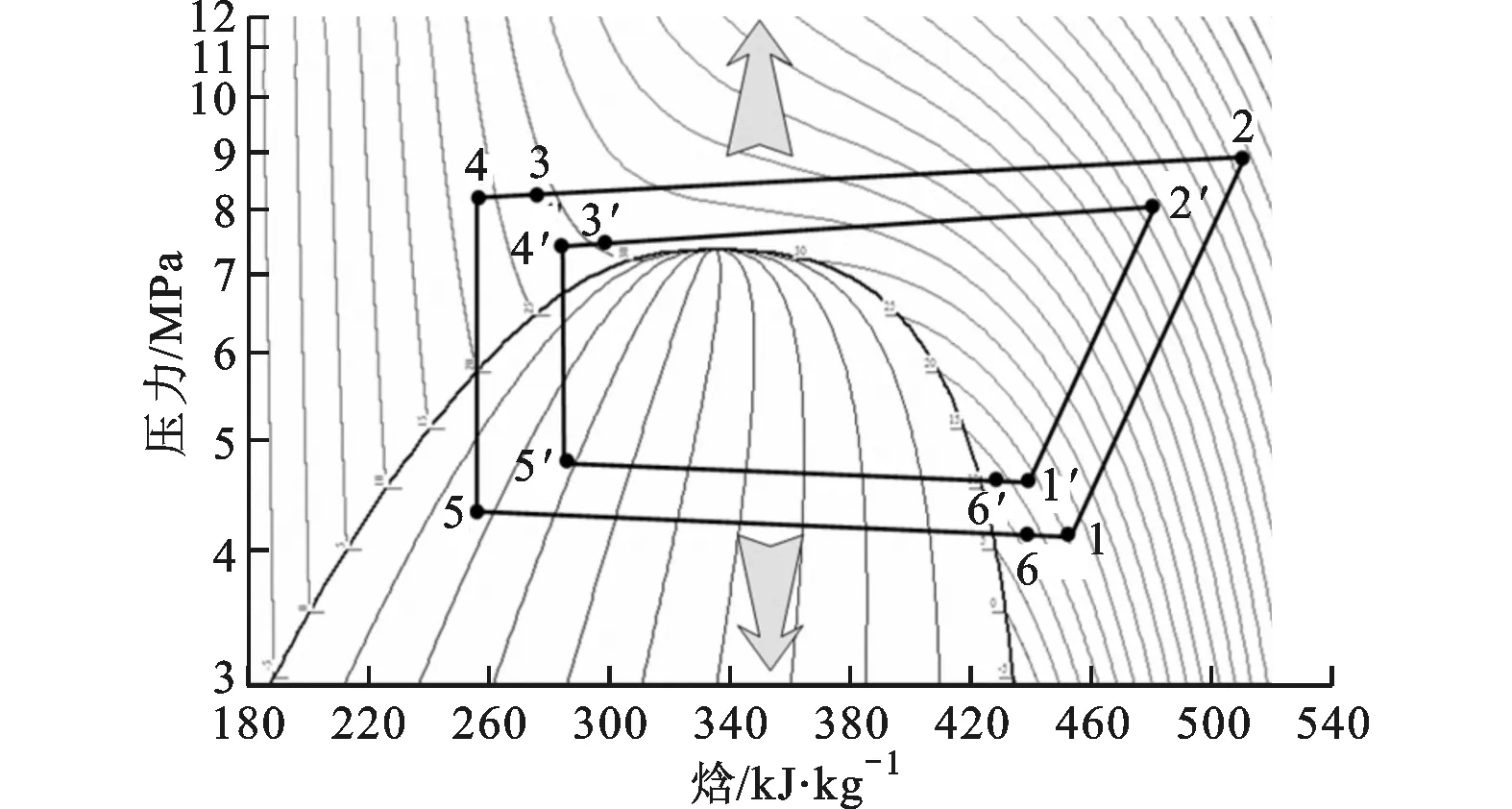
图10 CO2热泵系统蒸发压力随排压的变化

环境和进出水温度确定后,系统蒸发压力随排压的变化如图10所示,图中3-4为过冷段,6-1为过热段。实验中减小膨胀阀开度可使排压升高,但由于节流作用增强而压缩机质量流量减小量很小(压缩比变化量很小),所以蒸发压力逐渐下降。

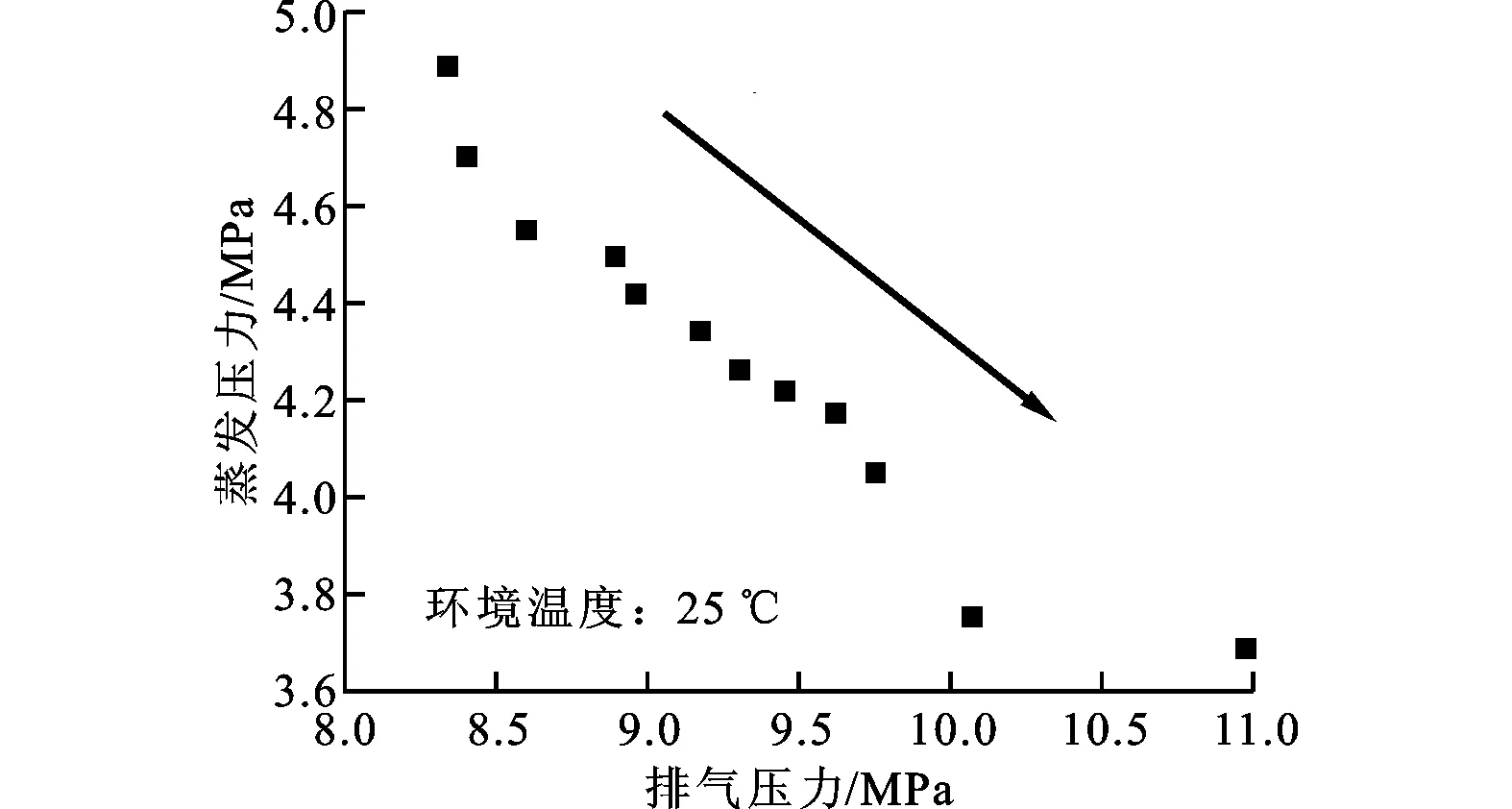
图11 进水温度为12℃时蒸发压力随排压的变化

进水温度为12℃、出水温度为60℃时,蒸发压力随排压的变化如图11所示。从图11可以看出,随着排压的升高,蒸发压力逆向减小。

2.4 排压对过热度的影响

文献中对于吸气过热度随排压的变化鲜有提及[10-11]。进水、出水温度为12、60℃时,吸气的温度和过热度随吸气压力的变化如图12所示。从图12可以看出,随着吸气压力的降低,吸气温度逐渐降低,吸气过热度升高。其原因是气冷器出口温度受限于进水温度,当蒸发压力降低时,蒸发器出口的CO2温度大幅降低,中间换热器内的换热必然导致吸气过热度升高。此分析中,蒸发压力的降低对应着排压的升高。

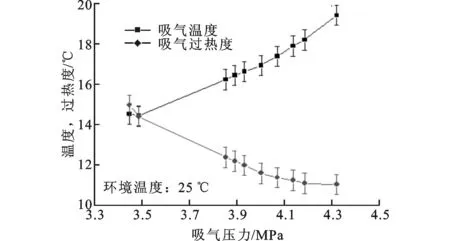
图12 吸气的温度和过热度随吸气压力的变化

2.5 排压对制冷剂侧气冷器出口温度的影响

环境与进出水温度一定时,CO2在气冷器出口的温度随排压的变化如图13所示。从图13可以看出,随着排压的升高,气冷器出口温度呈现出先急剧降低而后减缓且逐渐接近进水温度的过程。因为随着排压的升高,压缩比增大,质量流量降低,气冷器内制冷剂的减少造成了气冷器出口温度急剧降低,但受水侧进水温度的限制,气冷器出口温度最终会接近进水温度。

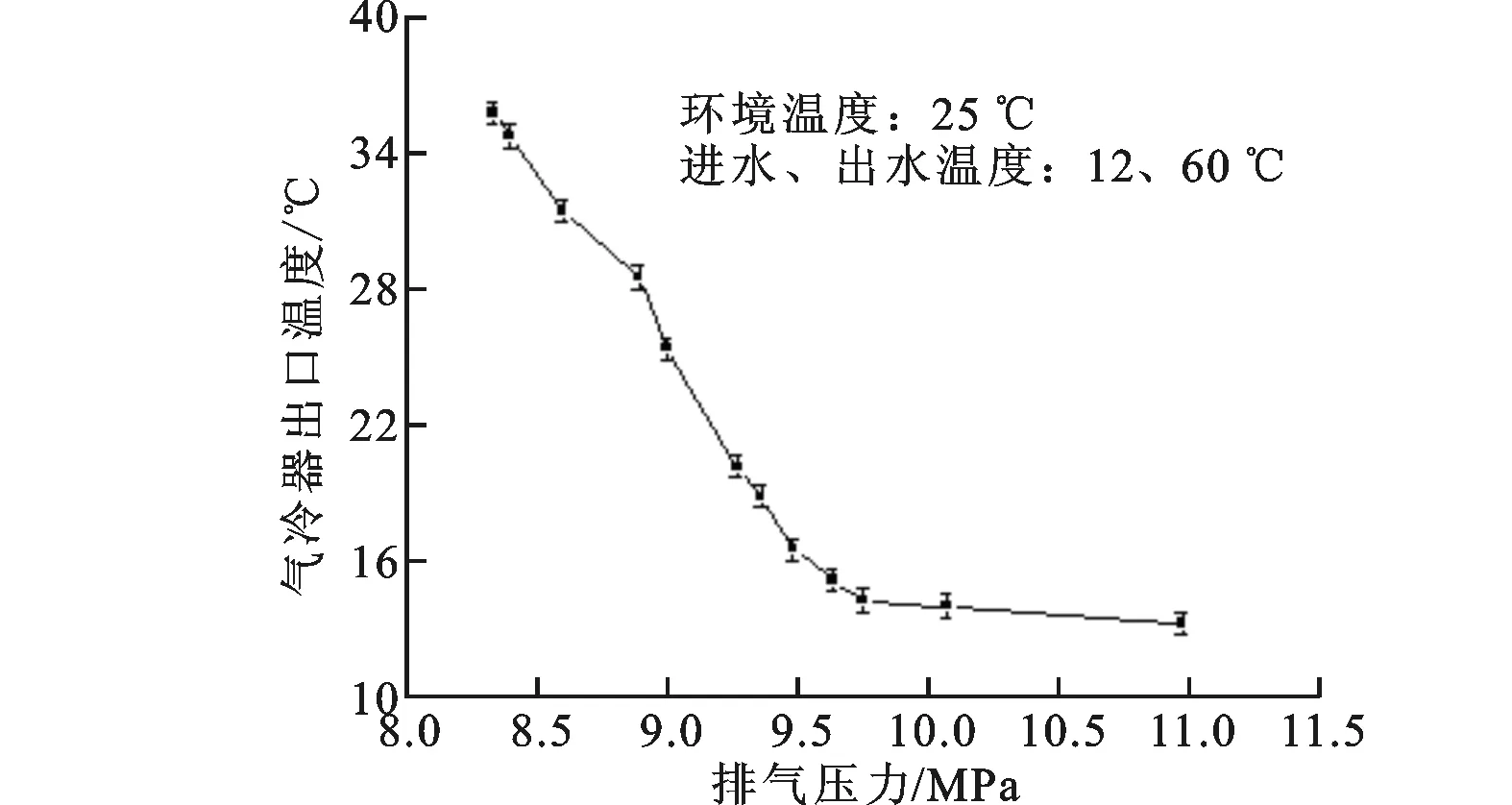
图13 气冷器出口温度随排压的变化

根据图13中实验结果,在确定运行工况下的最优排压为9.233MPa时,对应气冷器出口温度为19.8 ℃。可见,在某一确定运行工况下,最优排压对应着唯一的气冷器出口温度,但并非意味着气冷器出口温度决定着系统最优排压的大小。因此,以CO2在气冷器出口温度来预测系统最优排压必然产生较大误差。

由以上分析可知,若系统正常运行的排压与最优排压相差较大,则制热量、吸气过热度、气冷器出口温度等会大幅变化,最终影响COP。所以,正确预测系统最优排压并使系统运行在最优及临近最优排压是必要的。

3 跨临界CO2热泵最优排压分析

3.1 基于实验的最优排压分析

如图14(图中点P为排气点2对应的排压点)所示,考虑到实际运行中排压对系统吸气过热度、等熵效率、换热器压降等参数的影响,将最优排压引申如下:

(1)随着排压升高,吸气过热度增大,Δh1增大,Δh2减小,系统COP提高,实际的最优排压增大;

(2)假设等熵效率为定值,Δh2增加量减小,该假设下得到的最优排压高于实际的最优排压;

(3)气冷器出口温度逐渐降低,气冷器出口温度不变的假设实际上是Δh3增加量减小,该假设条件下得到的最优排压高于实际的最优排压;

(4)由于压降存在,所以相同气冷器出口温度下的焓差减小,即Δh3减小,该假设条件下得到的最优排压低于实际的最优排压。

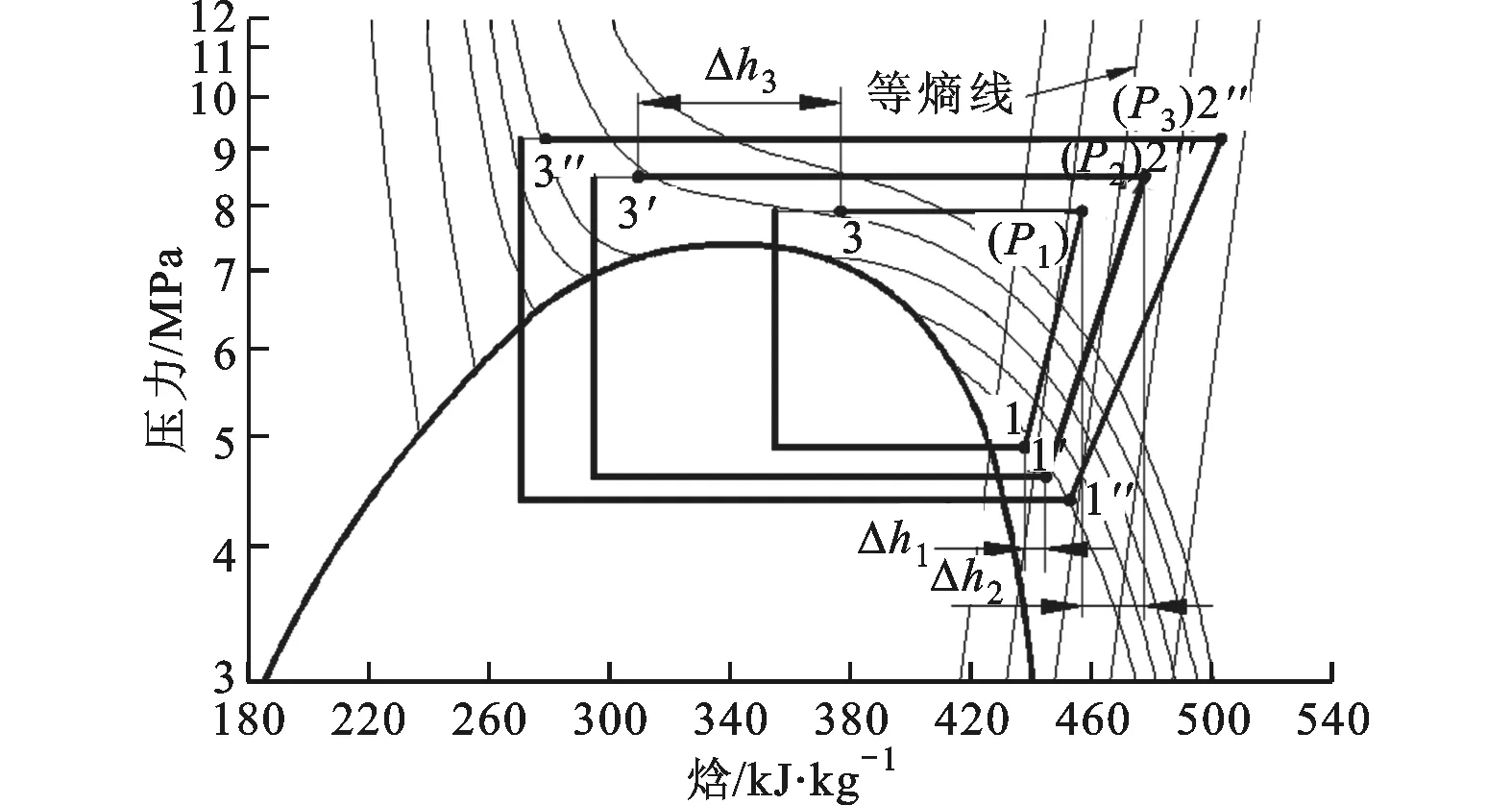
图14 系统主要参数随排压的变化

3.2 影响最优排压的外部因素

3.2.1 环境温度对最优排压的影响[4-5]根据以上研究可知,在确定的系统中,环境和进出水温度确定时,最优排压只有一个。进水、出水温度分别为12、75℃时,不同环境温度下系统COP随排压的变化如图15所示。从图15可以看出,随着环境温度的升高,系统最优排压逐步升高。高环境温度意味着高蒸发温度,此条件下达到相应最优排压所需的压缩比小于较低蒸发温度工况。较低蒸发温度下的吸气过热度要大于较高蒸发温度的吸气过热度,因此较低蒸发温度下需要的排气温度在较低排压下即可达到,这是最优排压随环境温度升高而升高的缘故。

假设压缩机绝热效率不变,达到相同的排气温度时低蒸发温度工况需较大的压缩比。如图16所示,点P′压力低于高蒸发温度所对应的最优排压点P的压力。实际上,系统等熵效率随压缩比的增加而减小,使得达到相同的排气温度下的排压降低至点P″的压力。

由于远离临界点时等温线变化相对陡峭,因此在环境温度较低时,相同压缩比下排气温度的升高要远远高于环境温度较高时的情况。因此,随着蒸发温度的降低,压缩比增大,等熵效率下降,系统最优排压随着环境温度的降低呈现出相同的变化趋势。

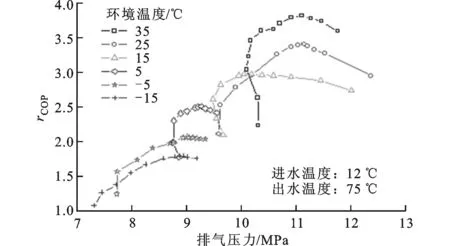
图15 不同环境温度下系统COP随排压的变化

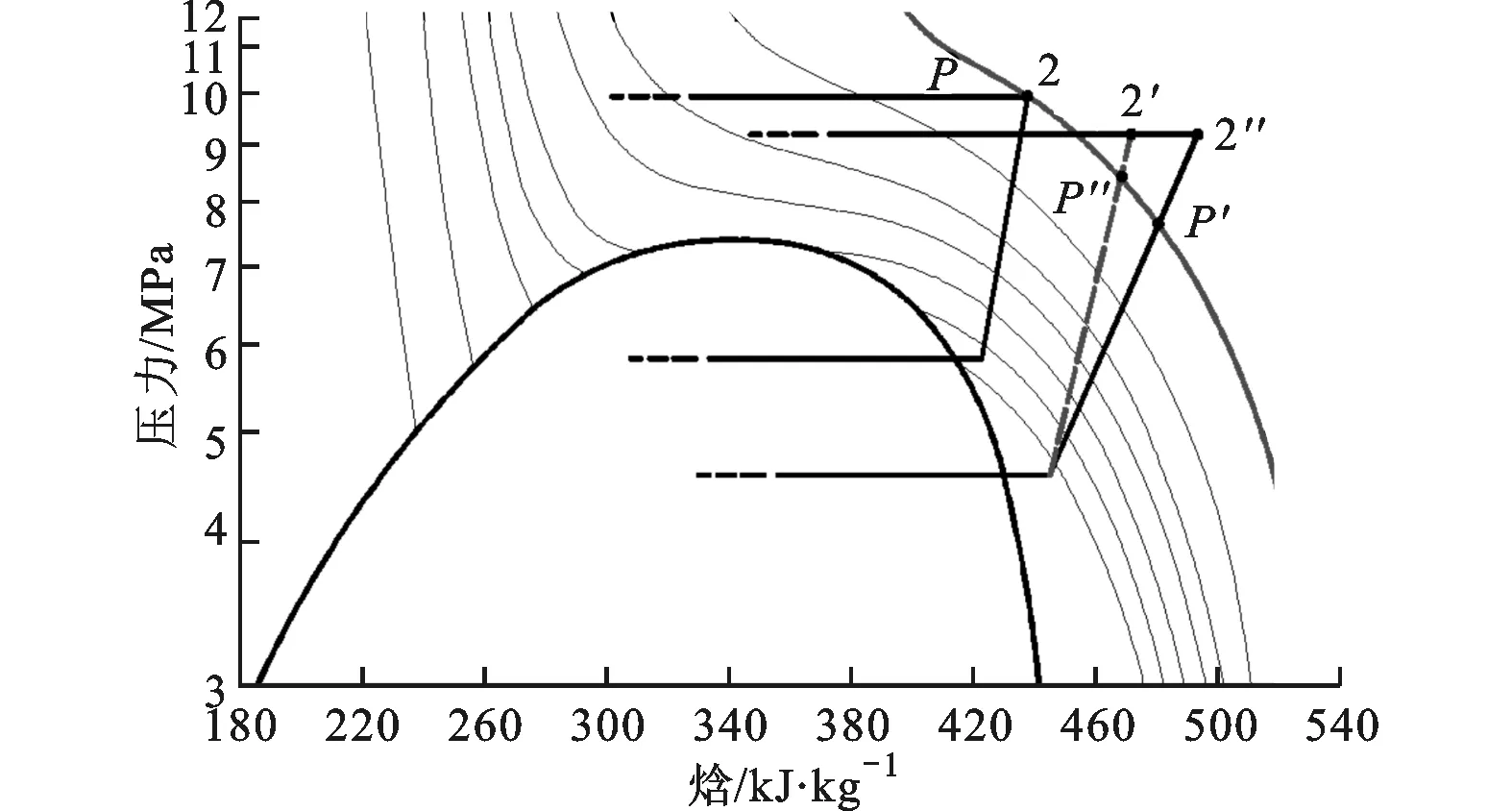
图16 环境温度对最优排压的影响

3.2.2 出水温度对最优排压的影响 环境温度一定、进水温度为12℃时,不同出水温度下系统COP随排压的变化如图17所示。从图17可以看出:最优排压随着出水温度的升高而升高;每一个确定的环境和出水温度对应着唯一的最优排压。其原因在于出水温度升高,排气温度升高,在确定的环境温度下最优排压必然升高。

3.2.3 进水温度对最优排压的影响 CO2在气冷器出口的温度总是趋近于进水温度,在确定的气冷器几何参数下,进水温度越低,气冷器出口温度越低,气冷器内制冷剂焓差的变化越大,系统最优排压降低。

另一方面,气冷器出口的CO2将进入中间换热器,进水温度越高,气冷器出口的制冷剂温度越高,中间换热器对应的低压侧CO2出口温度升高,即吸气过热度升高,进而排气温度升高。

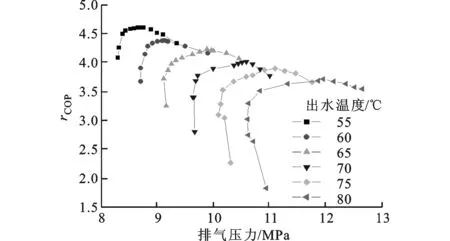
(a)环境温度为35℃

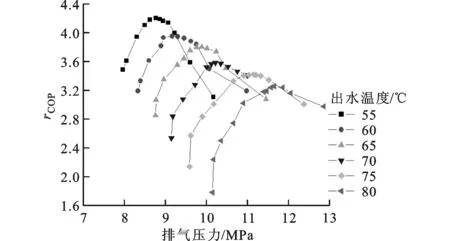
(b)环境温度为25℃

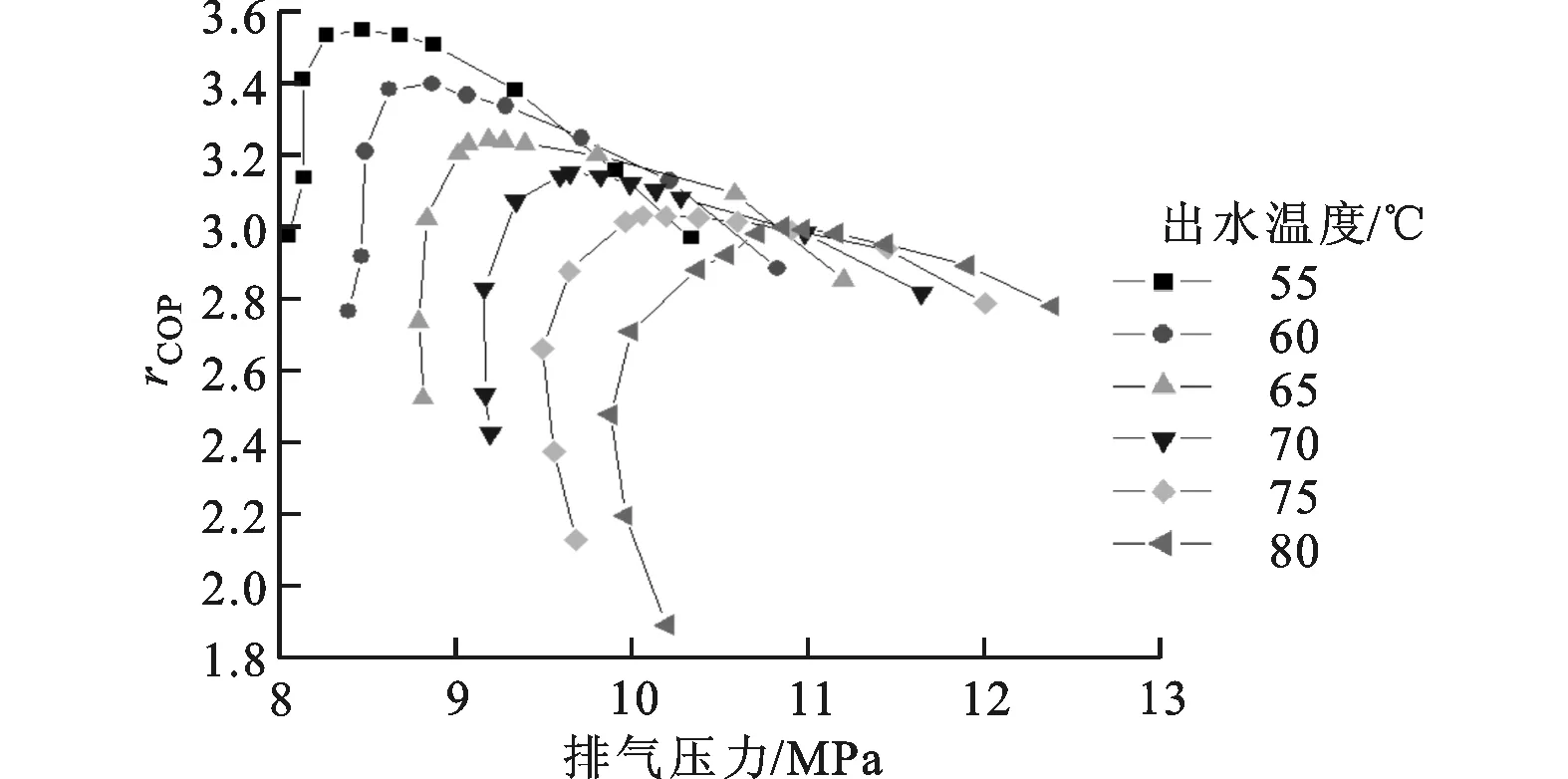
(c)环境温度为15℃

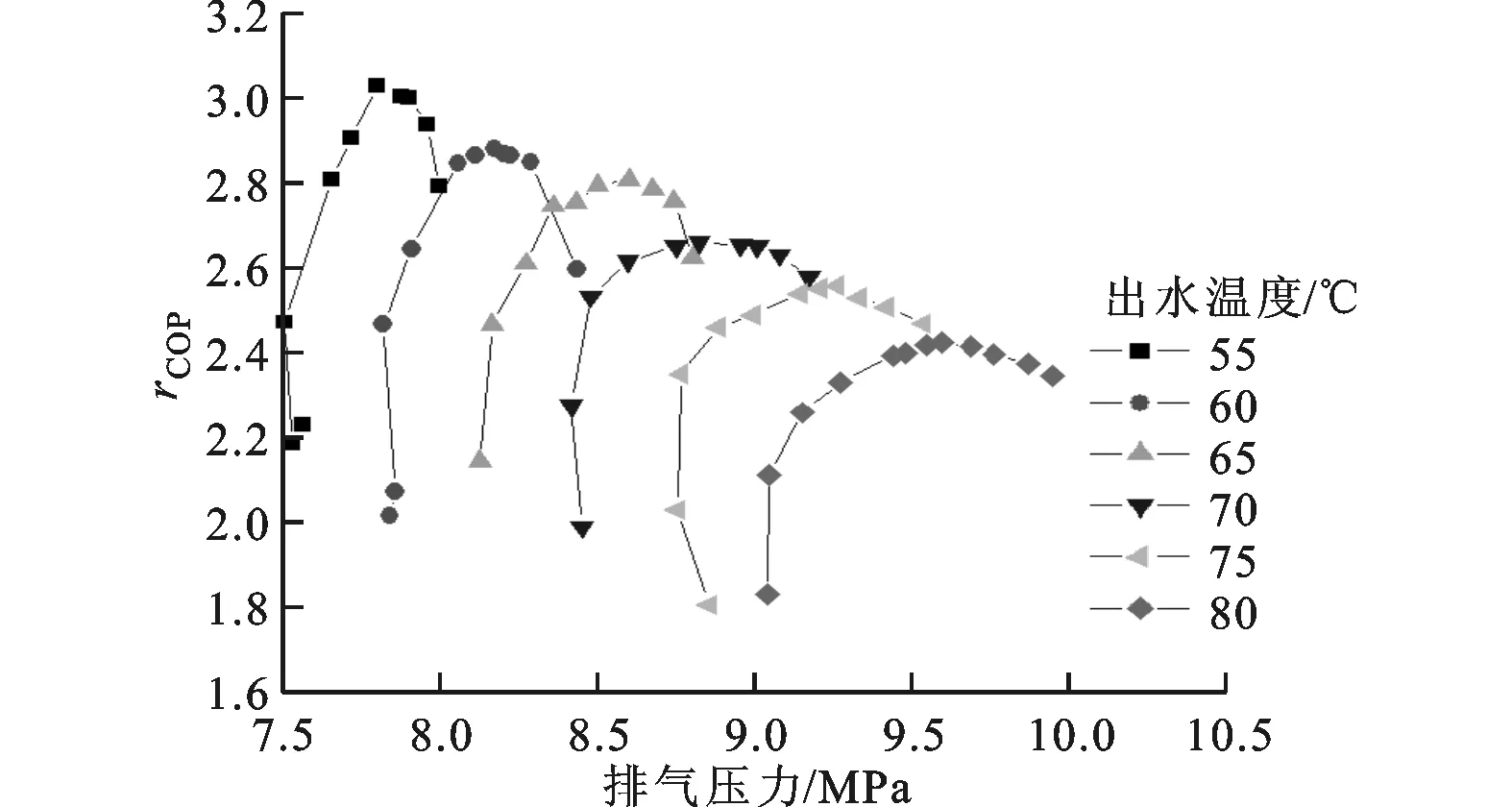
(d)环境温度为5℃

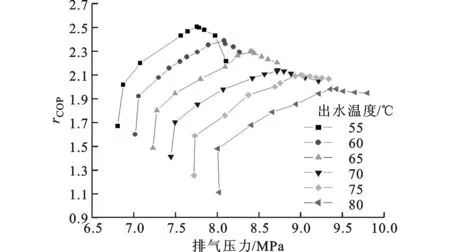
(e)环境温度为-5℃

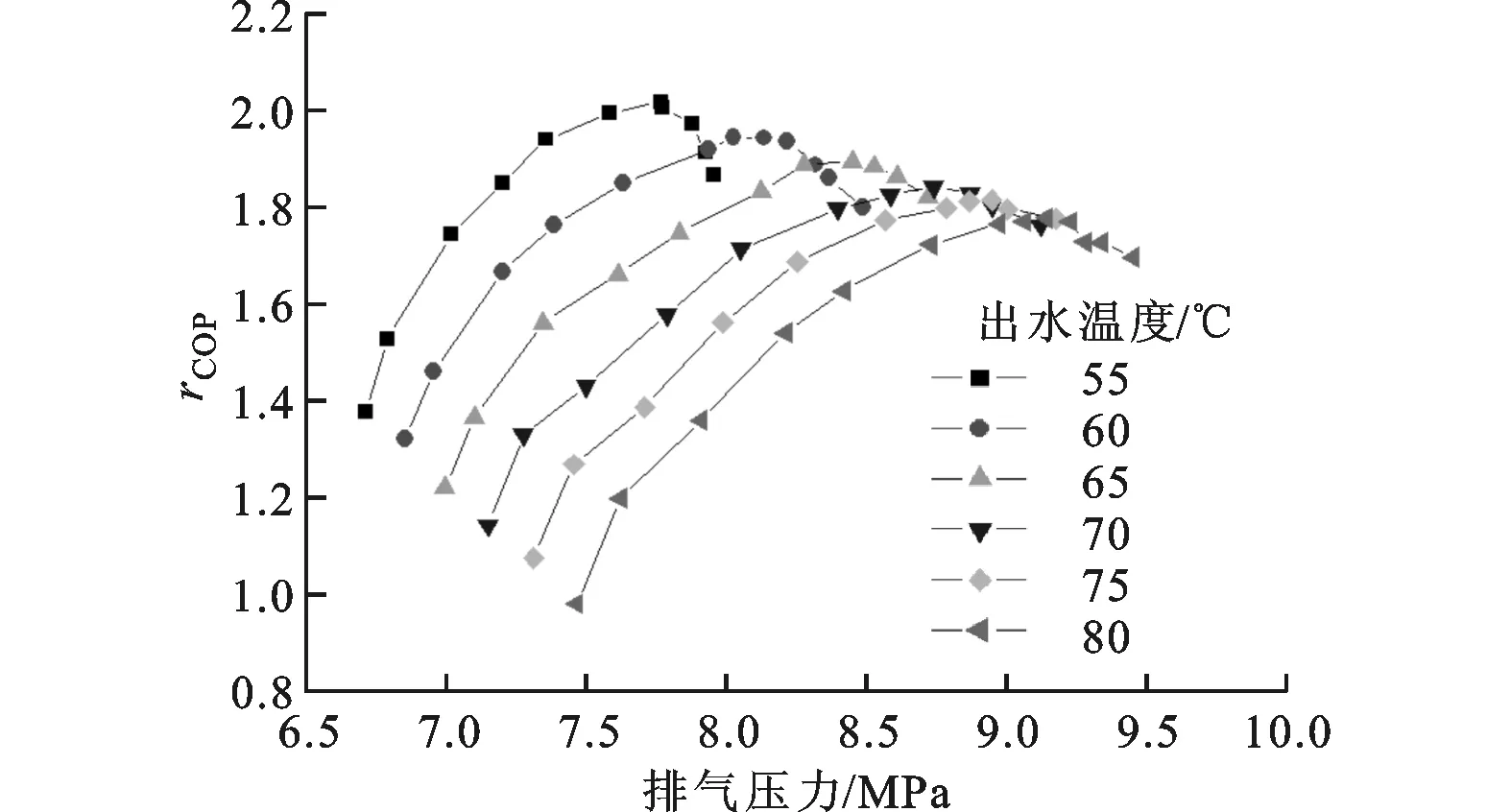
(f)环境温度为-15℃

4 最优排压控制关联式的建立与分析

综上可以看出,出水温度或环境温度上升均导致最优排压升高,如图18所示。

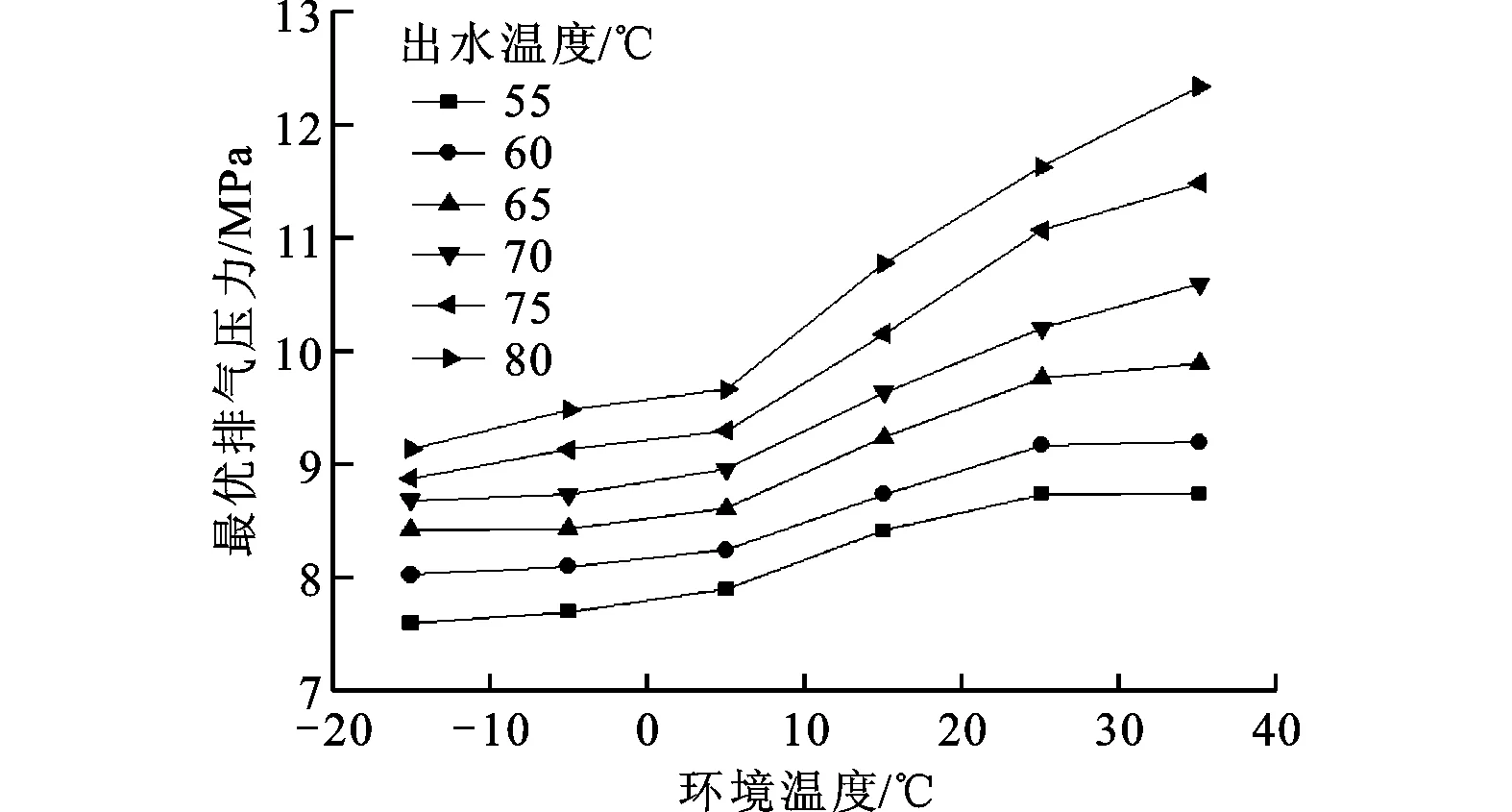
图18 不同出水温度下最优排压随环境温度的变化

文献中关于最优排压的研究大多以CO2在气冷器出口的温度和蒸发温度为自变量,或取其中的一个参数作自变量来建立函数关联式[3-6]。然而,实验证明,在确定的环境和进出水温度下,蒸发温度随着排压的变化而变化,如果用蒸发温度作为自变量去预测最优排压,那么在确定环境和进出水温度下会造成多个最优排压。

经过本文分析,在确定的环境和进出水温度下,跨临界CO2热泵存在着唯一的最优排压。因此,当进水温度变化相对较小时,可将环境温度和出水温度作为最优排压函数的自变量。结合实验数据,本文通过曲线拟合的方法建立了如下函数关联式(关联式中全等号仅表示数值上相等)

popt≌10.979 95+1.06442tw,out+

(1)

popt≌23.08391+1.22378tw,out-

(2)

式中:popt(105Pa)为最优排压预测值;tw,out(℃)为出水温度;tair( ℃)为环境温度。式(1)适用于5℃≤tair≤35℃的情况,式(2)适用于-15℃≤tair≤5℃的情况。

通过对比最优排压预测值和实验值发现,在环境温度为35℃、出水温度为80℃时,二者出现最大偏差,此时最优排压预测值小于实验值,偏差为5.5%,该预测值下系统COP仅比实验值小1.3%。因此,由大量实验结果拟合得到的关于最优排压的关联式完全适用于本实验样机。

5 结 论

本文研究得出了以下结论。

(1)针对空气源跨临界CO2热泵系统,从理论分析和实验验证方面得出系统中最优排压的存在性及唯一性。

(2)根据实验数据分析,探讨了跨临界CO2热泵系统中压缩机排压对系统主要性能的影响:随着排压的上升,系统制热量先上升后下降,蒸发压力不断降低,吸气过热度增大,气冷器出口温度降低,COP存在一个最大值。

(3)通过实验研究了影响最优排压的主要因素,其中环境温度与气冷器出水温度的影响最大。结合大量的实验数据,通过曲线拟合的方法得到了在一定温度范围内适用的最优排压预测关联式。

值得指出,系统组件特性会影响最优排压,包括压缩机绝热效率、容积效率和气冷器换热面积、几何结构等[4-7],本文关联式只适用于本实验样机或相同配置的系统,推广性有限。但是,以环境温度及出水温度为自变量,从实验结果中拟合得到的适用于某类系统的最优排压关联式的思路,是值得同行参考的。

[1] LORENTZEN G. Trans-critical vapour compression cycle

device: Switzerland, WO 90/07683[P]. 1990-07-12.

[2] LORENTZEN G, PETTERSEN J. A new, efficient and environmentally benign system for car air-conditioning [J]. International Journal of Refrigeration, 1993, 16(1): 4-12.

[3] KAUF F. Determination of the optimum high pressure for transcritical CO2refrigeration cycles [J]. International Journal of Thermal Sciences, 1999, 38: 325-330.

[4] LIAO S M, ZHAO T S, JAKOBSEN A. A correlation of optimal heat rejection pressures in transcritical carbon dioxide cycles [J]. Applied Thermal Engineering, 2000, 20: 831-841.

[5] SARKAR J, BHATTACHARYYA S, GOPALM M R. Optimization of a transcritical CO2heat pump cycle for simultaneous cooling and heating applications [J]. International Journal of Refrigeration, 2004, 27: 830-838.

[6] CHEN Y, GU J. The optimum high pressure for CO2transcritical refrigeration systems with internal heat exchangers [J]. International Journal of Refrigeration, 2005, 28: 1238-1249.

[7] GE Y T, TASSOU S A. Control optimization of CO2cycles for medium temperature retail food refrigeration systems [J]. International Journal of Refrigeration, 2009, 32: 1376-1388.

[8] CECCHINATO L, CORRADI M, COSI G, et al. A real-time algorithm for the determination of R744systems optimal high pressure [J]. International Journal of Refrigeration, 2012, 35(4): 817-826.

[9] 林高平, 顾兆林. 跨临界CO2制冷循环性能的研究 [J]. 西安交通大学学报, 1998, 32(8): 35-38.

LIN Gaoping, GU Zhaolin. Performance of Super-critical CO2refrigeration cycle [J]. Journal of Xi’an Jiaotong University, 1998, 32(8): 35-38.

[11]ZHANG X P, FAN X W, WANG F K, et al. Theoretical and experimental studies on optimum heat rejection pressure for a CO2heat pump system [J]. Applied Thermal Engineering, 2010, 30: 2537-2540.

(编辑 苗凌)

TheoreticalandExperimentalInvestigationforOptimalDischargePressureofAir-SourceTrans-CriticalCO2HeatPump

SONG Yulong1,TANG Xueping2,WANG Shouguo1,YANG Dongfang1,CAO Feng1

(1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. Jiangsu White Snow Electrical Limited by Share Ltd., Changshu, Jiangsu 215500, China)

To reveal the main factors of the optimal discharge pressure in a trans-critical CO2heat pump system, the heating performance is tested in enthalpy difference laboratory. The results show that the evaporation pressure and temperature in gas-cooler outlet decline with increasing discharge pressure; the superheat increases with discharge pressure; the heating capacity and the coefficient of performance (COP) increase firstly and then drop when discharge pressure rises, indicating that an optimal value exists. According to the test data, it is found that the optimal discharge pressure drops with declining environment temperature, inlet water temperature and outlet water temperature. At unchanged inlet water temperature (ambient water temperature), an experimental correlation taking environment temperature and outlet water temperature as independent variables is constructed by data fitting to predict the optimal discharge pressure. The experiments indicate that the COP difference between predicted optimal discharge pressure and actual optimal discharge pressure is less than 1.3%.

transcritical CO2heat pump; optimal discharge pressure; correlations

2013-11-10。

宋昱龙(1991—),男,硕士生;曹锋(通信作者),男,教授。

时间:2014-06-18

10.7652/xjtuxb201409014

TB61

:A

:0253-987X(2014)09-0081-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140618.1138.005.html