滚转角测量中直角棱镜相位损失及解决方法
2014-08-08李朝辉王昭黄军辉汤善治郭俊杰
李朝辉,王昭,黄军辉,汤善治,郭俊杰
(1.西安交通大学机械工程学院, 710049, 西安; 2.陕西恒通智能机器有限公司, 710049, 西安)
滚转角测量中直角棱镜相位损失及解决方法
李朝辉1,王昭1,黄军辉1,汤善治2,郭俊杰2
(1.西安交通大学机械工程学院, 710049, 西安; 2.陕西恒通智能机器有限公司, 710049, 西安)
在利用正交偏振光外差干涉相位法测量数控机床滚转角误差的过程中,发现反射元件直角棱镜造成的相位损失对系统分辨率产生了不可忽略的影响,通过琼斯矩阵运算,量化了该相位损失对实验结果的影响,并进行了实验验证;同时,针对相位损失问题,提出了基于高反膜相长干涉原理的解决方法。结果表明:直角棱镜引入的相位损失使测量系统在灵敏区的放大倍数降低了40.7%,而基于平面反射镜的解决方案基本消除了相位损失对测量系统分辨率的影响;滚转角误差引起的相位变化幅度由原来的55.8°上升到使用平面反射镜时的349.2°,与参考实验数据358.5°的变化幅度十分接近,从而证明了应用高反膜相长干涉原理解决相位损失问题的可行性。该原理和方法同时为解决全反射导致的光学相位变化问题提供了理论依据和解决思路。
滚转角;直角棱镜;相位损失;相长干涉;平面反射镜
机床滚转角的测量在机床误差检测中是一个棘手的问题,目前基于正交偏振光的测量方法研究比较多,并有较好的应用前景[1-7]。利用激光偏振面对旋转的敏感性,光路中传感元件的旋转往往会引起正交偏振光光强、相位或频差的变化,利用这种效应恰好可以感应到与测量光束垂直方向上的角位移[8]。基于此原理,文献[5]提出了利用1/2波片作为传感元件的测量方法,该方法利用直角棱镜将光路折返,使测量光束两次通过1/2波片,从而进一步提高了系统的分辨率。在实际应用中发现方案所用直角棱镜使入射光的相位发生了变化,降低了测量系统的分辨率。
本文基于文献[5]提出的测量方案,针对直角棱镜在光路折返中引入的相位损失问题,利用琼斯矩阵方法建立了数学模型,分析、量化了相位损失对实验结果的影响,同时针对相位损失问题提出了基于高反膜相长干涉原理[9]的解决方案,并通过实验验证了理论分析模型的正确性和解决方案的可行性。
1 滚转角测量
1.1 测量原理
机床滚转角的测量方案如图1所示。氦氖激光器发出的正交线偏振光经消偏振分光棱镜后一部分透射过去,另一部分反射出去,其中反射光作为参考光经过检偏器后直接被光电接收器接收;透射光作为测量光首先经过1/4波片实现椭偏化,增大系统的放大倍数,再经过传感元件1/2波片,经直角棱镜折返再次通过1/2波片,最后经检偏器被光电接收器接收。当存在滚转角误差时,1/2波片随之发生旋转,进而引起测量光相对于参考光的相位发生变化,通过相位计检测该相位的变化量即可相应求取滚转角的大小。
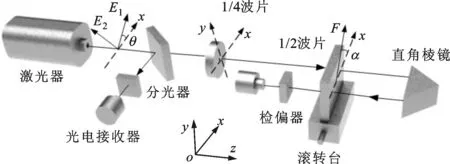
图1 滚转角测量光路图
1.2 数学模型
分别以1/4波片的快轴和慢轴为x轴和y轴、激光传播方向为z轴建立直角坐标系,其中偏振光E1与x轴的夹角为θ,1/2波片的快轴F与x轴的夹角为α,此处暂不考虑直角棱镜引入的相位损失,则激光束、1/4波片、1/2波片、旋转矩阵、检偏器的琼斯矩阵[10]依次为



其中光路在经过直角棱镜折返后,坐标系发生转换,如图2所示。此时1/2波片快轴和x轴的夹角变为-α,其琼斯矩阵变为

图2 直角棱镜引起的坐标变换

则光电接收器接收到的测量光信号为
Es=PH(-α)H(α)QR(θ)E0
(1)
假设所使用的光学元件为理想光学元件且光束垂直入射诸如1/4波片、1/2波片等光学元件,即不考虑光学元件的安装误差,将以上琼斯矩阵代入式(1),可得测量光束的光强为

φ1-φ2+ψ]
(2)
ψ=arctan(tanθtan4α)+arctan(cotθtan4α)
(3)
同理,可得参考光的光强为

(4)
由式(2)、(4)可得测量光相对于参考光的动态相位差为ψ。
对式(3)两边取微分可得系统的放大倍数为

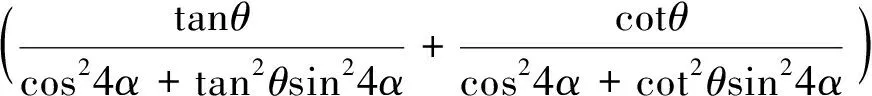
(5)

K=4(tanθ+cotθ)
(6)


(7)
2 直角棱镜引入的相位变化
2.1 直角棱镜问题理论分析
在目前所有采用该方案的文献中,均基于以上讨论没有考虑作为反射元件的直角棱镜对光路的影响,但是直角棱镜本身对入射光偏振状态的影响不能忽略。
反射元件的琼斯矩阵为

式中:δp为光波的p光分量在反射过程中发生的相位变化;δs为光波的s光分量在反射过程中发生的相位变化。
光波在直角棱镜中发生两次全反射,当不考虑直角棱镜的安装位置误差时,两次反射的入射角相等,因此直角棱镜的琼斯矩阵可表述为

则基于上述光路模型的测量光束的琼斯矩阵运算表达式修正为

(8)
代入琼斯矩阵运算,可得测量光束相对于参考光束的动态相位差为
ψ′=tan-1{[(cos22αsin2δp-sin22αsin2δs)cosθ+
sinθsin4α(cos2δp+cos2δs)/2]/[(cos22αcos2δp-
sin22αcos2δs)cosθ-sinθsin4α(sin2δp+
sin2δs)/2]}-tan-1{[(sin22αsin2δs-
cos22αsin2δp)sinθ+cosθsin4α(cos2δp+
cos2δs)/2]/[(sin22αcos2δs-cos22αcos2δp)sinθ-
cosθsin4α(sin2δp+sin2δs)/2]}
(9)
系统的放大倍数可表述为

(10)
同理,其在敏感区的放大倍数可简化为

(11)
利用菲涅尔公式[11],在全反射时有
2(δs-δp)=79.34°
代入式(11),得

(12)
比较式(6)和式(12)可知:直角棱镜引入的相位损失使得滚转角测量系统在敏感区的放大倍数降低了40.7%。同时,由式(11)可知,p光和s光相对相位差越大,即相位损失愈严重,则函数cos2(δs-δp)取值愈小,滚转角在敏感区的放大倍数愈小,系统的分辨率相应愈低。
2.2 实验分析
考虑到纵向塞曼激光器中所用1/4波片的制造误差使出射光已经微椭偏化,因此具体实验中不再使用1/4波片;同时,为消除所用1/2波片制造精度问题对实验的影响,实验中以使用的1/2波片而非理想的1/2波片作为参考,来验证直角棱镜引入相位损失的理论分析模型的正确性。参考光路模型如图3所示。
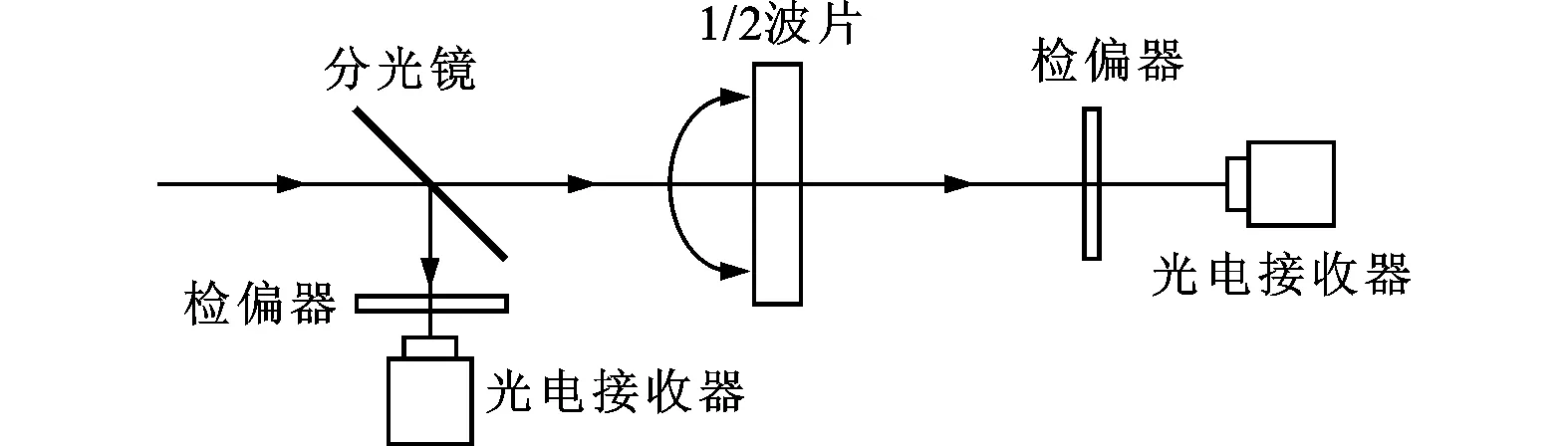
图3 参考光路模型图
图3中测量光束的琼斯矩阵运算表达式可表述为(此处将1/2波片看做一相位延迟量为δ的相位延迟器)
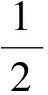

(13)
式中:ε为波片快轴与坐标系水平轴的夹角。
进一步计算可得测量光束的光强为
ω2)t+φ1-φ2+ψ1]
(14)
相应的动态相位差为
ψ1=tan-1[tan(δ/2)(cos2ε-sin2ε)]-
tan-1[tan(δ/2)(cos2ε+sin2ε)]
(15)
参考光路模型的实验值与理论值的对比如图4所示。
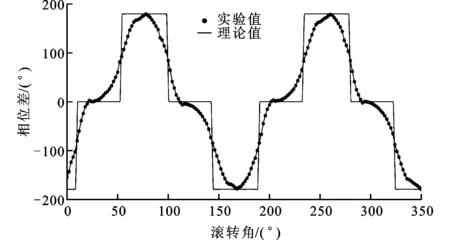
图4 参考光路实验值与理论值的对比图
由图4可知,由于1/2波片实际存在的制造误差,使得理论值与实验值存在一定的差别,故为了排除1/2波片的制造误差对结果的影响,将以图4中的实验数据为参考数据,来检验直角棱镜引入相位损失分析方法的正确性。
分析直角棱镜相位损失问题的实验光路模型如图5所示,基于该模型的测量光的琼斯矩阵运算表达式为

图5 相位损失分析光路图



(16)
则测量光束的光强为

(17)
其中

tan(δ/2)sin2θcos2δs)/(cos2δp+
tan(δ/2)cos2θsin2δp+tan(δ/2)sin2θsin2δs)]-
tan-1[(sin2δs+tan(δ/2)cos2θcos2δs-
tan(δ/2)sin2θcos2δp)/(cos2δs-
tan(δ/2)cos2θsin2δs+tan(δ/2)sin2θsin2δp)]
|rp|=|rs|=1
(18)
由上式可得,只有当满足以下条件时

(19)
才有

tan-1[tan(δ/2)(cos2θ+sin2θ)]

此时,相位损失的影响被消除。
现将理论值δs=-39.6708°,δp=-79.341 6°,δ=180°代入式(18),即可得到存在相位损失时的理论值,将其与实验值进行对比,如图6所示。
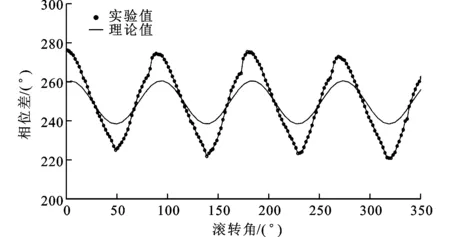
图6 相位损失分析模型的实验值与理论值对比图
从图6可知,理论值和实验值在变化周期和趋势上相符,而峰峰值却存在较大差距。存在这种差距的原因是因为式(18)同时是光波进入直角棱镜的入射角、棱镜折射率和光波反射率的函数,而在具体实验中很难保证入射角为45°,并且一般的实验中|rp|≠|rs|≠1也是影响因素之一。模拟显示,通过对上述固定参数的理论值做适当修正,如入射角调整为44°,反射比系数之比|rs|/|rp|取为0.98,即可得到理论值和实测数值良好的对比效果,如图7所示。
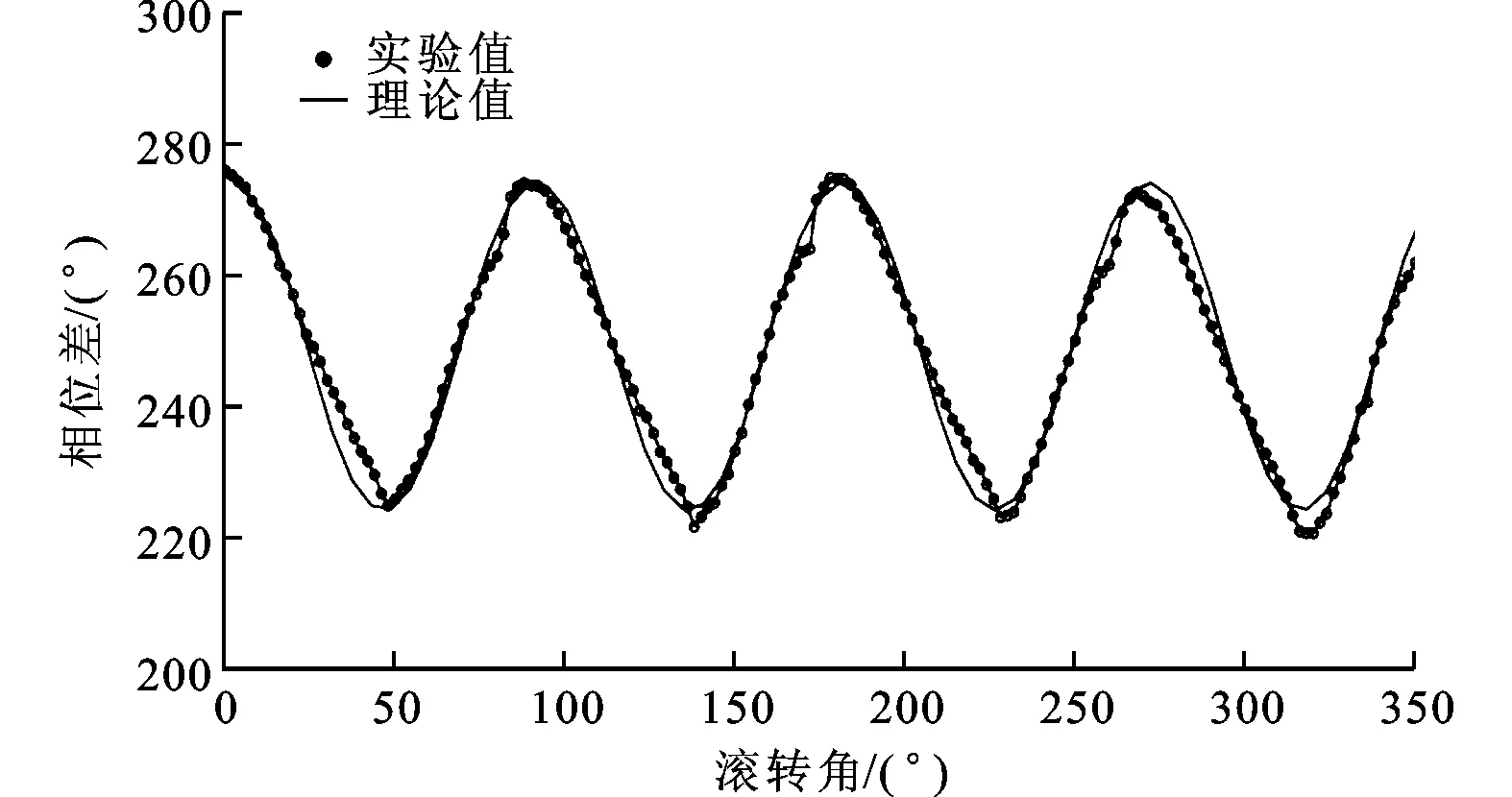
图7 参数修正后理论值与实验值的对比图
从图7可以看出,理论值和实验值有很好的相符性,进而证明了上文直角棱镜引入相位损失分析模型的正确性。
3 相位损失的补偿与消除
3.1 补偿原理
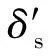
基于上述分析可知,满足式(19)时,即可消除相位损失对测量系统的影响。实际中,光波在两介质界面间的反射所引起的相位变化分别为(入射角小于布儒斯特角)δs=π和δp=0[11],二者均满足上述要求,同时结合多层介质高反膜的相长干涉原理可知,用两个相互垂直的平面反射镜代替(可以通过机械夹具实现)直角棱镜在理论上可以消除相位损失对实验的影响。
3.2 实验验证
基于上述思想,采用两个相互垂直的平面反射镜代替直角棱镜,并进行了实验验证,所获得的实验值与参考数据及直角棱镜实验值的对比如图8所示。

图8 两种反射器实验值与参考数据的对比图
由图8可知,使用平面反射镜作为反射器的实验值与参考数据有很好的相符性,与使用直角棱镜的实验值相比,实验结果有了本质上的改善,其相位变化幅度由普通直角棱镜的55.8°上升到349.2°,与参考数据358.5°的变化幅度十分接近,从而验证了使用平面反射镜作为反射器来解决相位损失问题的可行性。
4 结 论
本文主要从理论上分析了直角棱镜引起的相位损失对机床滚转角测量系统的影响并进行了实验验证,结果表明直角棱镜造成的相位损失严重降低了系统分辨率。针对该问题,本文提出了基于高反膜相长干涉原理的解决方案,即使用两个相互垂直的平面反射镜代替直角棱镜来解决相位损失问题,同时该方法也为其他折返光路中对相位有要求的情况提供了一种新的解决思路。
[1] 陈蕾, 张恩耀, 郭宏. 一种新的滚转角检测方法 [J]. 光电子激光, 2003, 14(6): 625-628.
CHEN Lei, ZHANG Enyao, GUO Hong. A novel method of rolling angle measurement [J]. Journal of Optoelectronics: Laser, 2003, 14(6): 625-628.
[2] LI Shiguang, YUAN Changxi, ZHANG Enyao, et al. Compact optical roll-angle sensor with large measurement range and high sensitivity [J]. Optical Letters, 2005, 30(3): 242-244.
[3] WU Chien-Ming, CHUANG Yi-Tsung. Roll angular displacement measurement system with microradian accuracy [J]. Sensors and Actuators: A, 2004, 116(11): 145-149.
[4] ZHANG S, LI K, REN M. Investigation of high-resolution angle sensing with laser mode split technology [J]. Applied Optics, 1995, 34(12): 1967-1970.
[5] 柳忠尧, 林德教, 殷纯永, 等. 高精度滚转角干涉仪 [J]. 光学技术, 2002, 28(4): 332-336.
LIU Zhongyao, LI Dejiao, YIN Chunyong, et al. High precision roll angle interferometer [J]. Optical Technique, 2002, 28(4): 332-336.
[6] 王昭, 汤善治, 高建民, 等. 一种基于阵列式多次反射的滚转角测量装置及方法: 中国, CN102654392A [P]. 2012-09-05.
[7] 王昭, 汤善治, 高建民, 等. 一种高分辨率的滚转角测量装置及测量方法: 中国, CN102818541A [P]. 2012-12-12.
[8] 任成, 谈宜东, 张书练. 正交偏振激光角度测量技术综述 [J]. 光子学报, 2010, 36(2): 193-199.
REN Cheng, TAN Yidong, ZHANG Shulian. Angle measurement based on orthogonally polarized laser [J]. Optical Technique, 2010, 36(2): 193-199.
[9] 唐晋发, 顾培夫, 刘旭, 等. 现代光学薄膜技术 [M]. 杭州: 浙江大学出版社, 2006: 107.
[10]钟丽红, 王昭, 汤善治, 等. 机床滚转角测量中敏感元件倾斜引起的误差分析 [J]. 西安交通大学学报, 2013, 47(5): 99-103.
ZHONG Lihong, WANG Zhao, TANG Shanzhi, et al. Measurement error analysis for machine tool roll error measurement due to inclined half wave plate [J]. Journal of Xi’an Jiaotong University, 2013, 47(5): 99-103.
[11]郁道银, 谈恒英. 工程光学基础教程 [M]. 北京: 机械工业出版社, 2007: 197.
(编辑 荆树蓉)
PhaseLossofRight-AnglePrisminRollAngleMeasurementandItsSolution
LI Zhaohui1,WANG Zhao1,HUANG Junhui1,TANG Shanzhi2,GUO Junjie2
(1. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. Shaanxi Hengtong Intelligent Machines Co. Ltd., Xi’an 710049, China)
The phase loss caused by the right-angle prism seriously affects the resolution of the roll angle measurement system based on the extrapolation interference method. The influence was quantified with Jones matrix and then experimentally verified. A scheme based on the constructive interference of the high-reflection films was also proposed to solve this problem. The results indicated that the amplification factor in the sensitive area was reduced by 40.7% due to the phase loss; Using two plane mirrors perpendicular to each other to replace the right-angle prism could basically eliminate the effects on the resolution of the roll angle measurement system caused by phase loss. The phase range was increased to 349.2° from 55.8° when the right-angle prism was replaced by the plan mirrors, which is close to the reference data 358.5°and hence the feasibility using constructive interference principle of high-reflection films to solve phase loss was proved. This method and theory can also provide a theoretical basis and solution thoughts for the optical phase loss induced by total reflection.
roll angle; right-angle prism; phase loss; constructive interference; plan mirror
2013-12-31。
李朝辉(1989—),男,硕士生;王昭(通信作者),女,教授,博士生导师。
国家科技重大专项资助项目(2012ZX04003071)。
时间:2014-06-13
10.7652/xjtuxb201409019
TH741.2
:A
:0253-987X(2014)09-0112-05
网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140613.1457.002.html
