卷吸速度方向与椭圆短轴成一夹角的弹流润滑渐近网格加密算法

蒲伟,王家序,,周广武,李俊阳,褚坤明

(1.四川大学空天科学与工程学院, 610065, 成都; 2.重庆大学机械传动国家重点实验室, 404100, 重庆)

卷吸速度方向与椭圆短轴成一夹角的弹流润滑渐近网格加密算法

蒲伟1,王家序1,2,周广武1,李俊阳2,褚坤明1

(1.四川大学空天科学与工程学院, 610065, 成都; 2.重庆大学机械传动国家重点实验室, 404100, 重庆)

针对数值求解卷吸速度方向与椭圆短轴成一夹角的重载薄膜弹流润滑问题,提出将渐进网格加密(progressive mesh densification,PMD)算法的思想应用于此类问题的求解,建立了此类问题雷诺方程的离散差分格式,运用快速傅里叶变换算法计算点接触弹性变形,采用PMD网格跳转方法加速迭代收敛,最后得到此类问题的完全数值解和油膜形状分布图,并与前人的实验数据进行了对比分析。结果表明:在重载薄膜润滑条件下,数值求解结果与前人的实验结果相一致;与直接在最终网格上进行迭代相比,文中提出的方法可以在粗糙网格上迅速消除误差,为高密度网格提供更好的初值,从而使计算收敛速度提高1倍以上,证明了PMD算法在求解此类问题时具有良好的收敛性和有效性。

弹流润滑;渐进网格加密算法;卷吸速度;椭圆接触

弧齿锥齿轮和准双曲面齿轮等传动由于具有承载能力大、传动平稳等优点,已广泛应用于航空、航天、车辆、工程机械、矿山机械、机床等工程领域。此类传动件与普通圆柱齿轮及滚动轴承等传动件相比,润滑模型具有特殊性,其卷吸速度方向与接触椭圆短轴并不重合,而是成一夹角。因此,研究卷吸速度方向与椭圆短轴成一夹角的弹流润滑的高效、稳定数值解法,对揭示此类传动界面的润滑机理具有十分重要的意义。

在以往的点接触弹流润滑研究中,绝大部分学者针对卷吸速度方向与接触椭圆短轴重合的情况进行了深入的研究,并取得了一系列的研究成果[1-4]。然而,针对卷吸速度方向与椭圆短轴成一夹角的弹流润滑问题,研究进展则较为缓慢,特别是此类重载弹流润滑问题的稳定数值解法一直是弹流领域的挑战。Chittenden等曾采用直接迭代法分析了卷吸速度方向与椭圆短轴成一夹角的情况,但该方法只能针对轻载荷的情况进行分析[5]。Wang等采用多重网格法对此类问题进行了分析,得到了此类问题的完全数值解[6]。虽然多重网格法能很快消除迭代误差,加速计算收敛,但针对重载薄膜润滑问题时,收敛性却并不理想,而且多重网格法在迭代计算时通过在粗糙网格和精细网格之间反复转换来达到收敛精度,但由于在重载薄膜润滑时油膜厚度对网格密度变得极为敏感,因此在每一层网格所求得的收敛值之间差距变大,导致在反复跳转迭代时误差并不能减小,迭代时容易导致溢出或死循环[7]。Stahl等近期发表了卷吸速度方向与椭圆主轴成一夹角的情况的实验解,得到了几组油膜分布图及中心油膜厚度,结果表明卷吸速度方向对油膜形状及厚度均有显著影响[8]。渐近网格加密(progressive mesh densification,PMD)算法是朱东等在求解卷吸速度方向与椭圆短轴重合的润滑问题时提出的,该方法能够在保证数值精度的情况下显著加快求解过程,特别是对于重载超薄膜润滑[7]。但是,目前该算法仅局限于对卷吸速度方向与椭圆短轴重合的润滑问题的求解。

本文旨在将PMD算法的思想应用于求解卷吸速度方向与椭圆短轴成一夹角的弹流润滑问题,并将该算法的数值计算结果与Stahl等发表的实验数据[8]进行对比分析,以验证该算法在求解重载条件下此类润滑问题时的收敛性和正确性。

1 数学模型

1.1 接触几何模型

弧齿锥齿轮和准双曲面齿轮等传动的接触润滑问题可简化为如图1所示的椭圆接触模型,卷吸速度方向与椭圆的短轴成一夹角,a、b分别为赫兹接触椭圆的长、短轴,ue为综合卷吸速度,u、v为ue在x、y方向的分量。

图1 接触润滑的椭圆接触几何模型

1.2润滑基本方程[8]

等温条件下的点接触非稳态弹流润滑归一化雷诺方程为

(1)

式中:u=uecosθ;v=uesinθ。

油膜的几何方程为

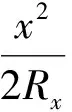
(2)

弹性变形方程为

压力黏度方程为

η=η0eαp

(3)

压力密度方程为

(4)

载荷平衡方程为

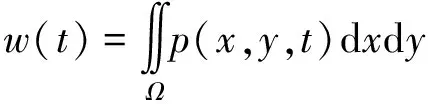
(5)

1.3 方程的归一化

将方程(1)～(5)中的量按下式进行归一化

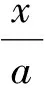
归一化后的雷诺方程为

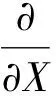
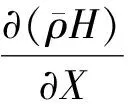
(6)

式中

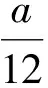
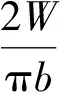
其他归一化方程皆由此方法推出,不再赘述。

2 数值计算

PMD算法的思想是将离散的润滑方程组在较小密度的网格(A网格)上进行迭代(见图2),当达到设定的收敛精度后,立即跳转到较大密度的网格(B网格)上进行迭代,在B网格根据A网格上迭代得到的油膜厚度和油膜压力值,通过插值的方法确定其他未知节点的油膜压力和油膜厚度,并以此作为B网格上迭代的初值,当在B网格上迭代达到收敛精度后,再如上述方法进行跳转,直到在预先设定的最终网格(最密网格)上得到收敛解。

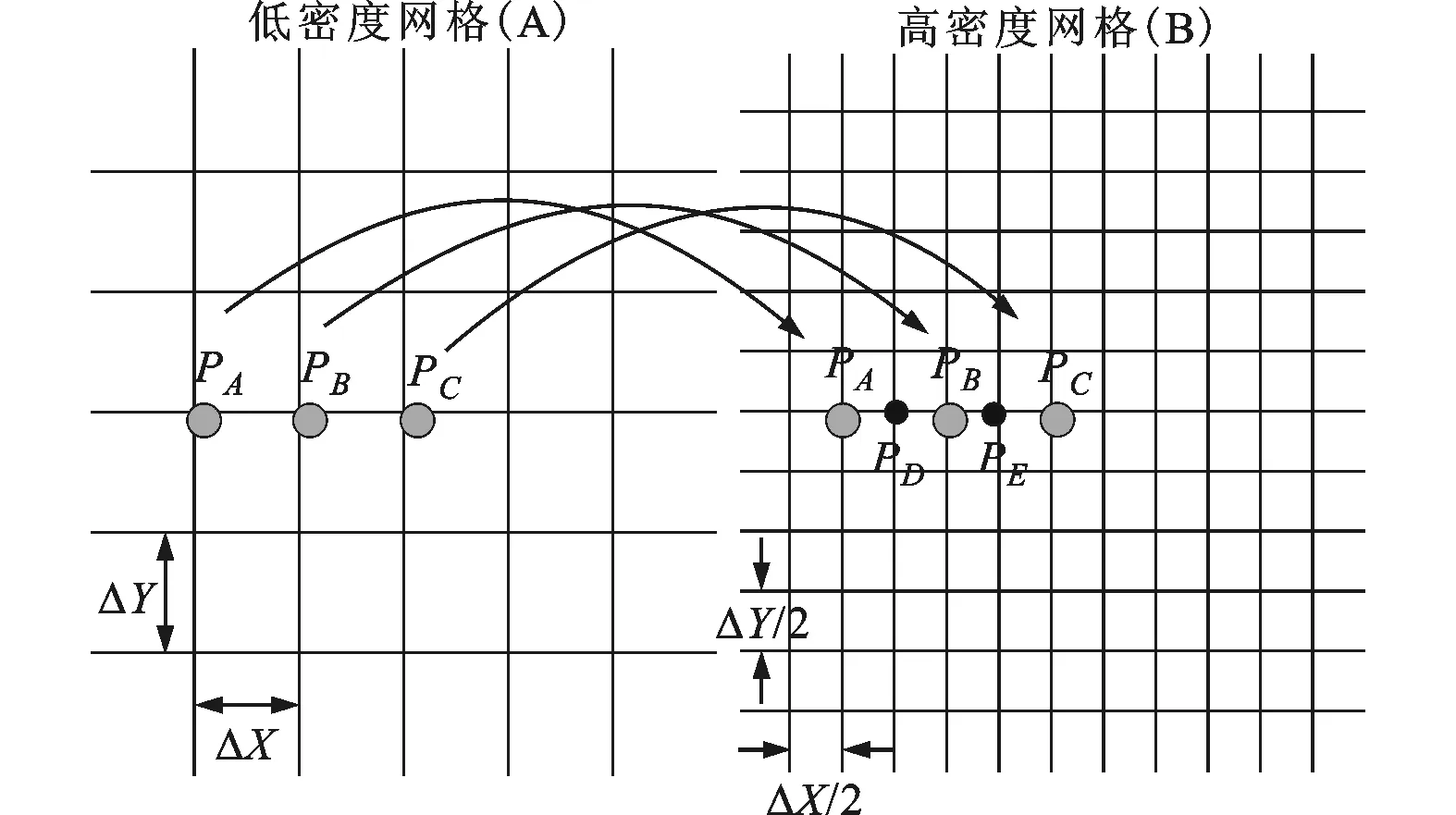
图2 PMD算法示意图

方程(1)～(5)中,弹性变形、润滑油黏度和密度都是压力的函数,将其与雷诺方程合并成一个微分积分方程组,采用复合迭代法[9]进行求解,其中弹性变形的计算采用的是快速傅里叶变换(FFT)方法[10]。求解时,在每一个未知节点压力处,将该微分积分方程组离散成一个差分方程[11],表达式为

Ai,jPi-1,j+Bi,jPi,j+Ci,jPi+1,j=Fi,j

(7)

式中:Ai,j、Bi,j、Ci,j、Fi,j为已知项,由已经求解出的压力分布算出;Pi-1,j、Pi,j、Pi+1,j是本次迭代需求解的未知量。

采用二阶中心差分方法,将雷诺方程中左边的压力流项离散[11]

式中

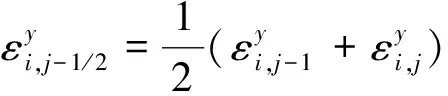
将离散的压力流拆分,按照式(3)的格式进行改写,并分散到各项系数中,结果如下

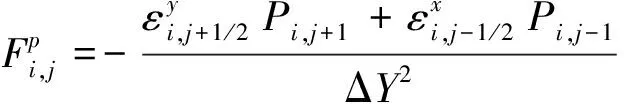
对雷诺方程右边的2项都分别采用一阶向后差分,然后按照式(7)的格式进行改写,并将其分散到各项系数中进行叠加,方法与上述相同,此处不再赘述。

未知节点的PD采用抛物插值方法求出

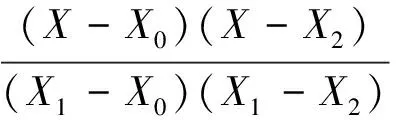
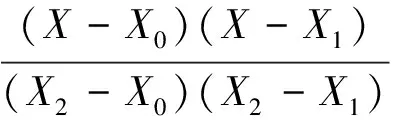
式中:X、X0、X1、X2分别为PD、PA、PB、PC在高密度网格中的横坐标。

未知节点PE的计算方法与PD的相同。采用上述插值方法,可将高密度网格上各节点的油膜压力和油膜厚度全部计算出来,然后进行迭代,直到达到设定的收敛精度。设定的收敛精度可取为

重复以上过程,直到达到设定的网格密度。由于网格密度每增加1倍,计算时间将会增加几倍,综合考虑计算时间和收敛精度,建议采用图3所示的3种网格密度进行迭代。

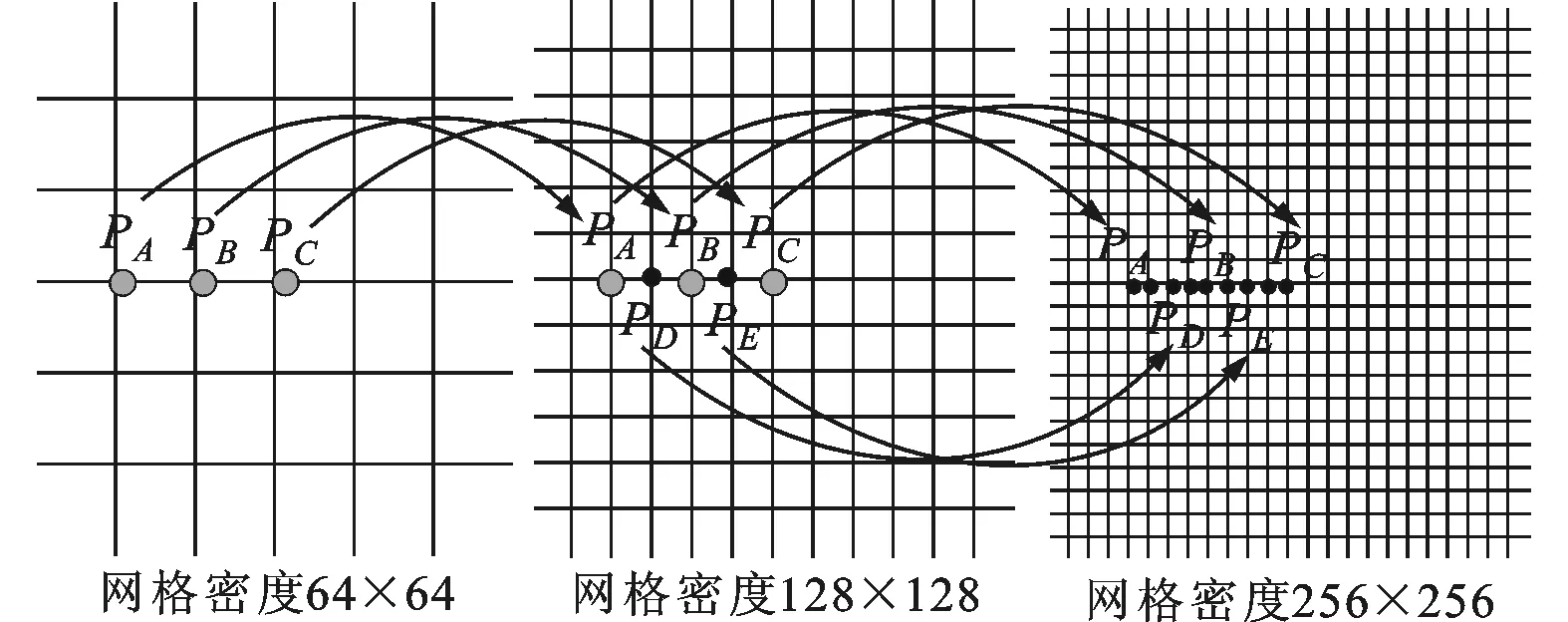
图3 用于迭代计算的3种网格密度

在迭代过程中,压力松弛因子ωp一般取0.005～0.3,在载荷大、膜厚小的情况下,ωp应取相对小的值;H0的修正因子ωh一般取0.001～0.01。计算流程图如图4所示。

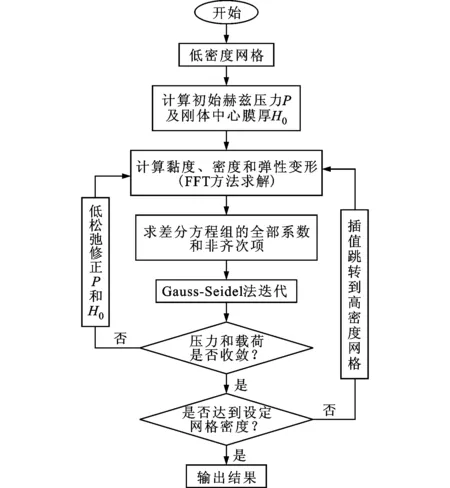
图4 计算流程图

3 结果与讨论

为了验证本算法在求解重载薄膜润滑时的收敛性和正确性,将本算法的数值仿真结果与Stahl等的实验结果[8]进行比较。数值仿真的相关输入参数与文献[8]中的实验参数保持一致,基本参数如下:θ={63.43°,73.90°,82.37°,90.00°},pH=1.03GPa,ue=0.6 m/s,Rx=4mm,Ry=12.7 mm,k=0.46;数值求解域为-2≤X≤2,-2≤Y≤2;采用3层网格,低密度网格参数为64×64,收敛精度为10-6;中密度网格参数为128×128,收敛精度为10-5;高密度网格参数为256×256,收敛精度为10-5;高密度网格有66 049个节点。数值仿真结果见表1～表4,对比结果如图5所示。

表1θ=63.43°时每一层网格上迭代收敛后的油膜厚度值

网格参数中心油膜厚度/nm最小油膜厚度/nm64×6420438128×12822860256×25623465

表2θ=73.90°时每一层网格上迭代收敛后的油膜厚度值

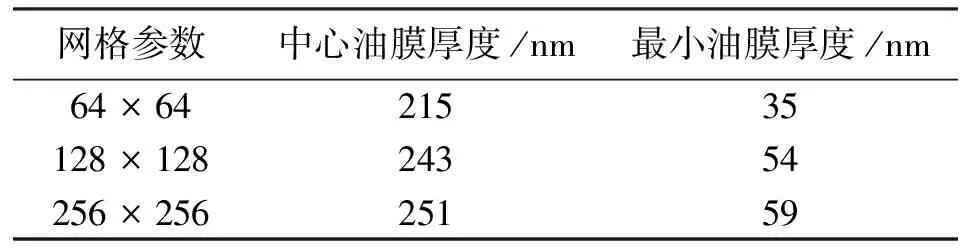
网格参数中心油膜厚度/nm最小油膜厚度/nm64×6421535128×12824354256×25625159

表3θ=82.37°时每一层网格上迭代收敛后的油膜厚度值

网格参数中心油膜厚度/nm最小油膜厚度/nm64×6422631128×12826753256×25627758

表4θ=90.00°时每一层网格上迭代收敛后的油膜厚度值

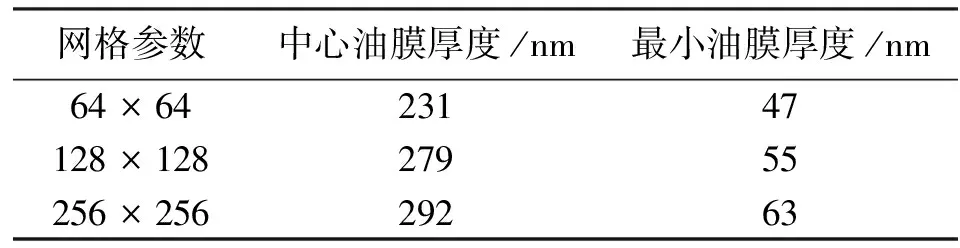
网格参数中心油膜厚度/nm最小油膜厚度/nm64×6423147128×12827955256×25629263

(a)油膜形状对比

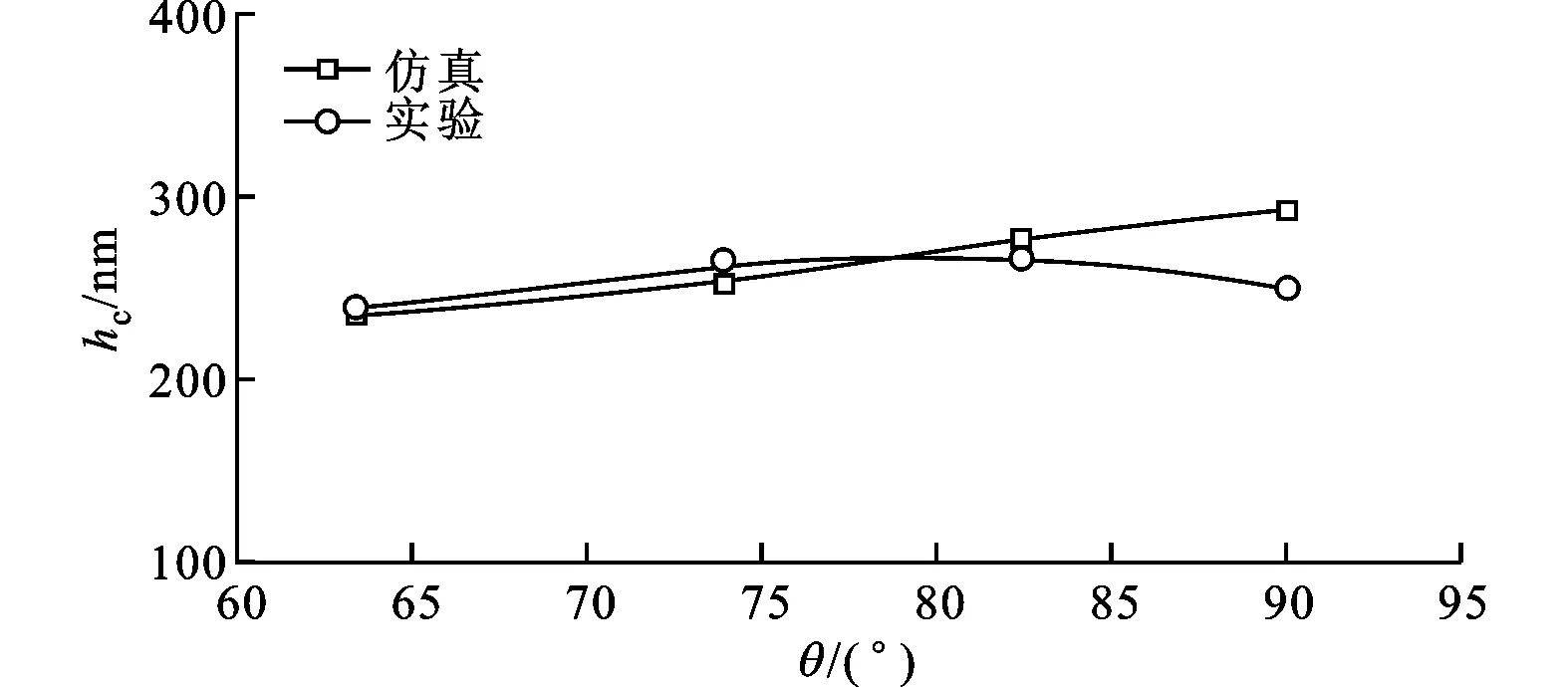
(b)中心油膜厚度对比

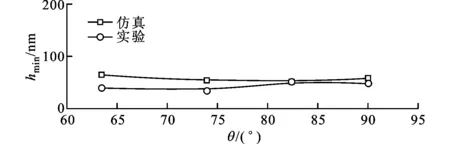
(c)最小油膜厚度对比

从表1～表4中可以看出,高密度网格层上迭代得到的油膜厚度值大于低密度网格层上迭代所得的油膜厚度值,且随着网格的逐渐加密,油膜厚度的增量逐渐减小,这与朱东等在研究卷吸速度方向与椭圆短轴重合时得出的结论[7]是一致的。综合考虑计算精度和计算时间,网格密度没有再进一步增大。

图5a为油膜形状对比,数值仿真图形采用了颜色渐变的方式来绘制。文献[8]中采用的椭球试件的表面粗糙度Ra=0.03μm。根据文献[12]可知,表面粗糙度对油膜厚度有一定影响,影响程度与表面的纹理和粗糙度大小有关。文献[8]的实验所用椭球试件的粗糙度较小,故对油膜厚度的影响程度也较小,可以用于验证弹流润滑模型的光滑解。从图5中可以看出,油膜形状随着卷吸速度方向的变化而变化,沿着润滑油流动的方向,弹流润滑出口区的间隙呈发散状,导致接触区的两侧面压力急剧下降而低于赫兹压力,使得固体表面产生突起,随着润滑油流动方向的改变,固体表面突起的位置不断变化,所以形成的油膜形状也随着流动方向发生变化。数值仿真得到的油膜形状及油膜厚度值都与文献[8]的实验结果相一致。算例的最大赫兹接触压力pH达到了1.03GPa,油膜厚度最小为40nm,收敛精度达到了10-5。

当卷吸速度方向与椭圆短轴成一夹角时,从前面的差分方程中可以看出,与卷吸速度方向重合于椭圆主轴时相比,离散方程(7)中多了雷诺方程中沿y方向的剪切流,从而加大了迭代系数矩阵的扰动,使得此联立方程组具有极强的非线性,而以往的数值方法在分析重载工况时收敛性并不理想。上述验证计算表明,PMD算法有效解决了这一难题,在粗糙的网格上能迅速消除迭代误差,为高密度网格提供更好的初值,从而可加速收敛。因此,针对卷吸速度方向与椭圆短轴成一夹角的弹流润滑,PMD算法在求解重载薄膜润滑时具有良好的加速收敛特性。

此外,为了进一步验证本算法的加速收敛性能,对2组算例进行了对比分析:一组算例使用PMD算法,采用3层网格,网格参数与前述例子相同;另一组算例直接在256×256的网格上进行迭代。基本输入参数如下:θ=50°,pH=2.02GPa,ue=0.5～15m/s,Rx=12.7 mm,Ry=36.1 mm,k=2。在相同收敛精度(10-5)下,计算结果如表5、表6、图6所示,其中t1是在256×256的网格上直接迭代的计算时间,t2是采用PMD方法的计算时间。

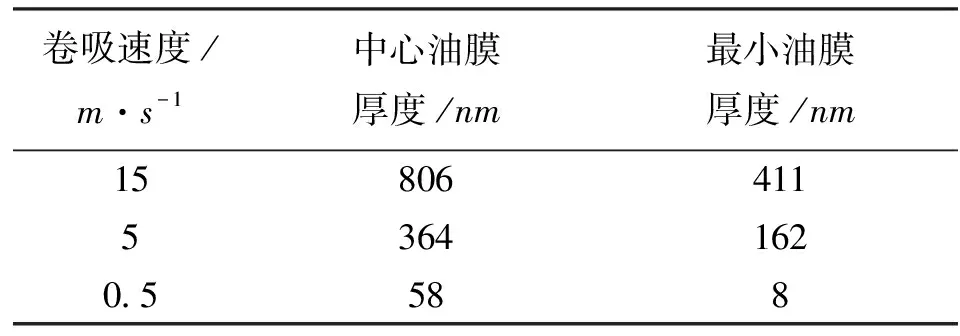
表5 PMD算法的计算结果

表6 相对计算时间

(a)ue=15m/s (b)ue=5m/s (c)ue=0.5m/s

从表6中可以看出,与直接迭代相比,采用PMD方法可使计算速度提高1倍以上,并能够显著加快收敛速度。此外,这2组算例的最大赫兹接触压力达到了2.02GPa,最小油膜厚度低至8 nm,进一步验证了PMD算法在求解重载薄膜润滑时具有良好的收敛性和有效性。

4 结 论

(1)本文给出了针对卷吸速度方向与椭圆短轴成一夹角时弹流润滑方程组的差分格式,得出了相应的PMD数值求解算法,包括插值、迭代跳转等具体步骤。

(2)将PMD算法求解的数值结果与Stahl等的实验研究结果[8]进行了比较,结果表明二者相当一致,证明对于重载薄膜润滑,PMD算法在求解卷吸速度方向与椭圆短轴成一夹角的弹流润滑问题时具有良好的收敛性和有效性。

(3)与直接在最终网格上进行迭代相比,针对卷吸速度方向与椭圆短轴成一夹角的弹流润滑问题,采用PMD算法可以在粗糙网格上迅速消除误差,为高密度网格提供更好的初值,从而显著提高计算收敛速度。

[1] ZHU Dong, WANG Jane Q. Elastohydrodynamic lubrication: a gateway to interfacial mechanics: review and prospect [J]. Journal of Tribology, 2011, 133(4): 1-14.

[2] HAMROCK B J, DOWSON D. Isothermal elastohydro-dynamic lubrication of point contacts: part I Theoretical formulation [J]. Journal of Lubrication Technology, 1976, 98(2): 223-228.

[3] HAMROCK B J, DOWSON D. Isothermal elastohydro-dynamic lubrication of point contacts: part II Ellipticity parameter results [J]. Journal of Lubrication Technology, 1976, 98(3): 375-381.

[4] 朱东, 温诗铸, 郑林庆. 热弹性流体动力润滑椭圆接触问题的完全数值解 [J]. 机械工程学报, 1984, 20(1): 1-15.

ZHU Dong, WEN Shizhu, ZHENG Linqing. A full numerical solution for the thermoelastohydynamic problem in elliptical contacts [J]. Chinese Journal of Mechanical Engineering, 1984, 20(1): 1-15.

[5] CHITTENDEN R J, DOWAON D, DUNN J F. A theoretical analysis of the isothermal elastohydrodynamic lubrication of concentrated contacts: II General case, with lubricant entrainment along either principal axis of the Hertzian contact ellipse or at some intermediate angle [J]. Proceedings of the Royal Society of London: A Mathematical and Physical Sciences, 1985, 397(1813): 271-294.

[6] WANG Jing, QU Shiyue, YANG Peiran. Simplified multigrid technique for the numerical solution to the steady-state and transient EHL line contacts and the arbitrary entrainment EHL point contacts [J]. Tribology International, 2001, 34(3): 191-202.

[7] ZHU Dong. On some aspects in numerical solution of thin-film and mixed EHL [J]. Proc Inst Mech Eng: Part J J Eng Tribol, 2007, 221(5): 561-579.

[8] STAHL K, MICHAELIS K, MAYER J. Theoretical and experimental investigations on EHL point contacts with different entrainment velocity directions [J]. Tribology Transactions, 2013, 56(5): 728-738.

[9] AI Xiaolan. Numerical analysis of elastohydrodynamically lubricated line and point contacts with rough surfaces by using semi-system and multigrid methods [D]. Evanston, IL, USA: Northwestern University, 1993.

[10]LIU Shuangbiao, WANG Qian, LIU Geng. A versatile method of discrete convolution and FFT (DC-FFT) for contact analysis [J]. Wear, 2000, 243(1): 101-110.

[11]REN Ning. Advanced modeling of mixed lubrication and its mechanical and biomedical applications [D]. Evanston, IL, USA: Northwestern University, 2009.

[12]ZHU Dong, HU Yuan-Zhong. Effects of rough surface topography and orientation on the characteristics of EHD and mixed lubrication in both circular and elliptical contacts [J]. Tribology Transactions, 2001, 44(3): 391-398.

(编辑 葛赵青)

ProgressiveMeshDensification(PMD)MethodinElastohydrodynamicLubricationofEllipticalContactswithArbitraryEntrainment

PU Wei1,WANG Jiaxu1,2,ZHOU Guangwu1,LI Junyang2,CHU Kunming1

To numerically solve the elastohydrodynamic lubrication problem that entraining velocity vector has an oblique angle with the minor axis of Hertzian contact ellipse under heavy loading and thin film lubrication conditions, the progressive mesh densification (PMD) method is used, and a discrete differential scheme for Reynolds equation is set up. The fast Fourier transform is adopted to calculate the elastic deformation for point contact, and the PMD method is used to accelerate the iterative convergence. Moreover, a complete numerical solution and the film thickness distribution are obtained and compared with the experimental results from literatures to validate the model. The results show that, under heavy loading and thin film lubrication conditions, this numerical solution is in accordance with the experimental results, proving that the PMD method is effective and has fine convergent behavior for solving this kind of problem.

elastohydrodynamic lubrication; progressive mesh densification method; entraining velocity; elliptical contact

2014-02-08。

蒲伟(1989—),男,博士生;王家序(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(51375506);教育部高等学校博士学科点专项科研基金资助项目(2012018113001);中央高校基本科研业务费专项资金资助项目(2014SCU11009)。

时间:2014-06-13

10.7652/xjtuxb201409016

TH132

:A

:0253-987X(2014)09-0095-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140613.1457.003.html