带Neumann边界条件的Extended Fisher-Kolmogorov系统的定态分歧

张 强, 曾 艳, 李桂花, 张黔川

(中国民用航空飞行学院计算机学院,四川广汉618307)

1 引言及预备知识

Extended Fisher-Kolmogorov(EFK)系统于19世纪80年代作为理论模型出现在相变以及其他双稳态现象中[1-3].在过去的几十年里,人们对EFK系统进行了广泛的研究,解的结构(如行波解)和解的渐进行为[4-9]成为研究的关注点,而对其分歧问题的研究则很少.分歧揭示了当控制参数穿越临界值时系统稳态解的变化规律.目前分歧理论[10-12]已广泛地应用于物理和生物等领域的研究中[13-15].文献[13]应用文献[10]的方法研究了一类非线性磁流变阻尼系统的局部分岔,不过注意到文献[13]考察的是一个有限维系统.而对于无穷维系统的分歧问题的研究,最近在文献[12]中给出了规范化的Lyapunov-Schmidt约化方法.应用该方法,文献[14]讨论了Kuramoto-Sivashinsky方程的分歧问题.文献[15]研究了基因繁殖在一平衡点附近的分歧.而本文应用此方法研究了EFK系统的定态分歧问题,得到了系统产生超临界和次临界分歧的完整判据、分歧解的表达式等结果,希望有助于加深对该方程动力学性质的理解.另外,在一定程度上也有助于理解类似的带有四阶导数项的反应扩散方程的动力学性质.

考虑下面EFK系统的定态分歧:

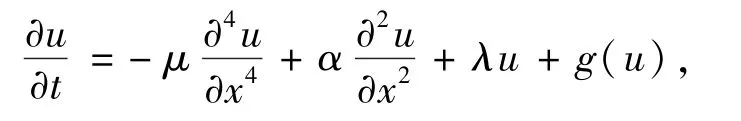
2 主要结果

致谢中国民用航空飞行学院面上项目(J2011-30)对本文给予了资助,谨致谢意.

[1]Coullet P,Elphick C,Repaux D.The nature of spatial chaos[J].Phys Rev Lett,1987,58(5):431-434.

[2]Dee G,Saarloose W.Bistable systems with propagating fronts leading to pattern formation[J].Phys Rev Lett,1988,60(25):2641-2644.

[3]Zimmermann W.Propagating fronts near a Lifschitz point[J].Phys Rev Lett,1991,66(11):1546-1546.

[4]Peletier L,Troy W.Spatial patterns described by the extended Fisher-Kolmogorov equation:periodic solutions[J].SIAM J Math Anal,1997,28(6):1317-1353.

[5]Tersian S,Chaparova J.Periodic and homoclinic solutions solutions of extended Fisher-Kolmogorov equations[J].J Math Anal Appl,2001,260(2):490-506.

[6]Rottschddotaer V,Wayne C.Existence and stability of traveling fronts in the extended Fisher-Kolmogorov equation[J].J Diff Eqns,2001,176(2):532-560.

[7]Kwapisz J.Uniqueness of the stationary wave for the extended Fisher-Kolmogorov eqaution[J].J Diff Eqns,2000,165:235-253.

[8]Bartuccelli M.On the asymptotic positivity of solutions for the extended Fisher-Kolmogorov eqaution with nonlinear diffusion[J].Math Meth Appl Sci,2002,25:701-708.

[9]罗宏,蒲志林.Extended Fisher-Kolmogorov系统的整体吸引子及其分形维数估计[J].四川师范大学学报:自然科学版,2004,27(2):135-138.

[10]Guckenheimer J,Holmes P.Nonlinear Oscillations,Dynamical Systems,and Bifurcations of Vector Fields[M].New York:Springer-Verlag,1997:117-226.

[11]钟承奎,范先令,陈文塬.非线性泛函分析引论[M].兰州:兰州大学出版社,1998:155-185.

[12]马天,汪守宏.非线性演化方程的稳定性与分歧[M].北京:科学出版社,2007:125-203.

[13]钟吉玉.关于Kuramoto-Sivashinsky方程平衡解的分岔问题[J].四川大学学报:自然科学版,2006,43(2):277-280.

[14]周钰谦,刘倩.一类非线性磁流变阻尼系统的局部分岔[J].四川大学学报:自然科学版,2008,45(2):241-244.

[15]李俐玫,魏纯辉.基因繁殖的在平衡点(0,0)附近的定态分歧[J].四川大学学报:自然科学版,2011,48(5):995-1000.