基于差分进化的离散粒子群算法求解TSP问题

付 聪，沙 伟，张海霞，杨 亚

（河海大学物联网工程学院，常州213022）

基于差分进化的离散粒子群算法求解TSP问题

付 聪，沙 伟，张海霞，杨 亚

（河海大学物联网工程学院，常州213022）

针对TSP问题，结合离散粒子群算法和差分进化算法各自的特点，提出了基于差分进化的离散粒子群算法。该算法先利用差分进化算法的变异、选择算子产生新的群体，再通过离散粒子群算法和交叉及选择算子进行局部搜索。通过对标准的30个城市进行实验，实验结果表明，该优化算法在求解TSP问题上有很好的性能。

优化算法；离散粒子群；差分进化；旅行商问题

1 引 言

TSP问题是诸多领域内出现的多种复杂问题的集中概括和简化，是图论、运筹学和组合优化中的NP难问题，常被用于对智能启发式算法有效性的验证。虽然它的数学描述很简单，但却很难精确求出最优解，另一方面很多研究领域出现的复杂优化问题可以被抽象概括为TSP问题加以求解，因此找到能够有效解决TSP问题的方法，在理论上和实际应用中都很有价值［1］。

目前求解TSP问题的算法大致可以分两类：一类是局部启发式算法，比如2-opt、3-opt、LK算法等，这类算法的优点是寻找最优解效率非常高，但是由于过分依赖于问题，容易陷入局部最优；另外一类是智能优化算法，例如遗传算法、差分进化算法、蚁群算法、粒子群算法等，这类方法独立于问题，目前已经取得了些阶段性的成果，而差分进化算法和粒子群算法都是近年的研究热点［2］。基于以上分析，提出基于差分进化的离散粒子群算法，并应用到TSP问题中，取得了满意的效果。

2 离散粒子群算法和差分进化算法

2.1 离散粒子群优化算法

Eberhart和Kennedy于1995年提出粒子群优化算法（Particle Swarm Optimization，PSO）［3］，该算法简单易实现且可调参数少。PSO算法最初被应用于连续空间的优化，研究也主要集中在连续函数方面，即其速度、加速度等状态都是连续的，它们的运算法则也是连续量的运算。然而，许多实际工程应用问题是离散的，变量是有限的，需要将基本PSO算法在二进制空间进行扩展。早在1997年，Kennedy和Eberhart就提出了PSO算法的离散二进制版［4］。在求解TSP问题方面，高尚，韩斌等［5］结合遗传算法、蚁群算法和模拟退火算法的思想，提出了一种混合粒子算法用于求解TSP问题，其中还讨论了多种交叉策略和变异策略。Clerc给出一种求解TSP问题的DPSO算法（TSP-DPSO）［6］，等等。

在TSP-DPSO算法中，粒子的位置用所有城市的一个排列来表示，则所有排列就构成了粒子的搜索空间。该算法引入了交换子和交换序列的概念，一个交换子S＝Swap（i，j）是指交换粒子第i个和第j元素的位置，一个交换子集则是指一组以特定顺序排列的交换子。粒子的速度则是指粒子为达到最优解而需要对当前位置执行的基本交换序。基于此概念，TSP-DPSO算法对粒子群中的加减法等操作算子进行了重新定义，其更新公式如下：

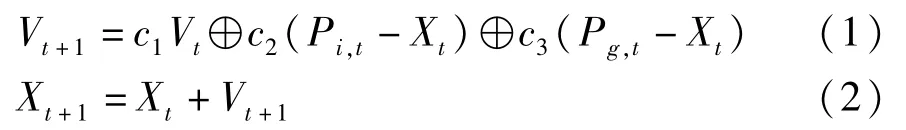
其中：粒子的位置和速度分别为Xt和Vt，均由0和1组成，c1、c2和c3是随机生成的学习因子；Pi，t和Pg，t则是粒子局部最优和全局最优值。这里，速度与随机数的数乘表示依随机数概率保留原速度中的交换子，算子⊕为粒子速度间的异或操作。

该算法通过对粒子位置和速度矢量的操作，实现了连续粒子群向离散空间的映射。但实验结果表明，在解决TSP问题时该算法并非最优算法。

2.2 差分进化算法

差分进化算法（Differential Evolution，DE）是一种新兴的进化计算技术，它是由Storn等人于1995年提出的［7］，最初的设想是用于解决切比雪夫多项式问题，后来发现DE也是解决复杂优化问题的有效技术。

DE算法是一种随机的并行直接搜索算法，有3种运算贯穿着整个算法的执行过程：变异、交叉和选择。算法首先利用在搜索空间内随机选取两个向量的差值与第3个随机选取向量的加权求和来实现群体变异，然后通过比较由交叉算子生成的个体和相应父代个体的适应值优劣来保存优秀个体，如此反复迭代，不断进化，向最优解逼近［8］。整个运行过程中群体的规模保持不变。3种操作描述如下：

（1）变异

对于个体xi（t），根据下面公式生成变异个体：

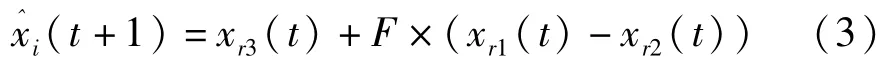
其中：xr1，xr2，xr3为从进化群体中随机选取的互不相同的3个个体，并且i和r1、r2、r3之间必须是不同的。因此，一个群体中个体的数量必须多于4个。F为缩放比例因子，用于控制差向量的影响大小。

（2）交叉

为了增加群体的多样性，交叉操作被引入差分进化算法。将个体xi（t）和变异个体进行二项分布杂交生成杂交个体。

操作公式如下：

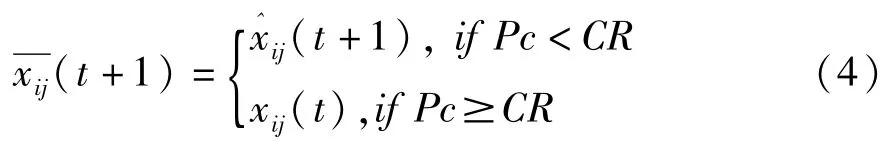
其中：D为解空间维数，CR∈［0，1］，为交叉概率，Pc是［0，l］之间的随机数。

（3）选择

在基本差分进化算法中，选择操作采取贪婪策略，即只有当产生的子代个体优于父代个体时（对应目标函数值f（xi（t＋1））≤f（ti（t）））才被保留，否则父代个体被保留至下一代。

3 基于差分进化的离散粒子群优化算法

为了改善DPSO的全局搜索性能，改进算法应考虑以下两个方面：迭代初始阶段在保证一定收敛速度的同时应尽量避免粒子“早熟”，引导粒子探索新的区域并尽可能让粒子足迹遍历整个解空间；搜索后期当算法达到一定收敛精度时，若粒子陷入局部最优则通过更换粒子或重新调整算法参数引导粒子逃离局部最优区，以进一步提高DPSO的收敛精度［9］。

相比于其他进化算法，DE算法的变异算子有利于增加全局搜索能力，保证种群的多样性；交叉算子可以提高局部搜索能力，加快收敛速度；选择算子具有一定的记忆能力，能够保留优秀个体［10］。

基于前文对DPSO和DE算法特点分析，提出基于差分进化的离散粒子群优化算法（简称DEDPSO），在离散粒子群优化算法中引入差分进化算法，作为种群信息更新方式，将DE全局信息收集机制与DPSO寻优搜索机制相结合。

DEDPSO算法的具体步骤总结如下：

（1）在搜索空间内，初始化群体的位置和速度，以及粒子群种群规模和最大迭代次数等参数；

（2）变异和选择，根据公式（3）更新群体的位置，并更新群体最优点；

（3）根据公式（1）（2）更新群体的位置和速度；

（4）根据公式（4）对位置进行交叉和选择；

（5）满足结束条件或达到最大迭代次数，则输出结果，否则转至步骤（2）。

4 基于差分进化的离散粒子群算法求解TSP问题

文中提出了基于差分进化的离散粒子群算法求解TSP问题。以标准的30个城市进行试验，初始粒子种群大小为200。表1为基于差分进化的离散粒子群算法求解TSP问题的运算结果，600、1000和1500是程序运行的代数，Average为10组数据的平均值，N为10次搜索，搜索到最优值的次数，初始种群大小同样设置为200，缩放比例大小设为0.1，交叉概率大小设置为0.6，还是采用标准的30个城市，它的最优值为423.74。

表1 基于差分进化的离散粒子群算法效果表

两种算法分别连续运行10组，运行600次后，DEDPSO的10组数据平均值比DPSO的10组数据平均值明显要小。此时虽然DEDPSO搜索到全局最优值的次数还较少，但是搜索结果已经很接近全局最优值。运行1000次后，可以看出此时10组1000次DEDPSO搜索结果平均值更加接近全局最优值，并且10次搜索结果中有6次搜索到了全局最优值。当运算代数达到1500时，10次搜索有8次搜索到最优值，也就是基本每次都能搜索到最优值。

基于上述分析，可以知道基于差分进化的离散粒子群算法在相同的运行次数内提高了优化质量，在城市数目较少的情况下，更加容易搜索到TSP问题的最优值。

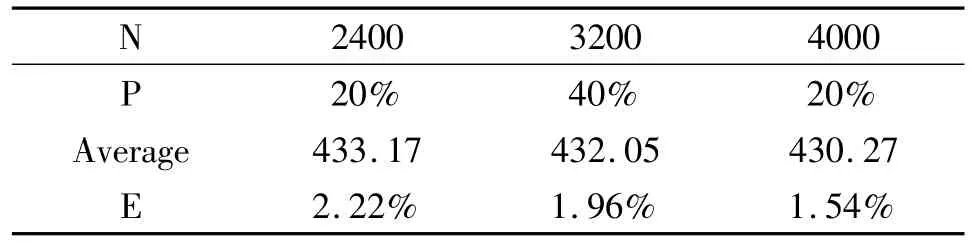
表2 DPSO多粒子群运算效果表

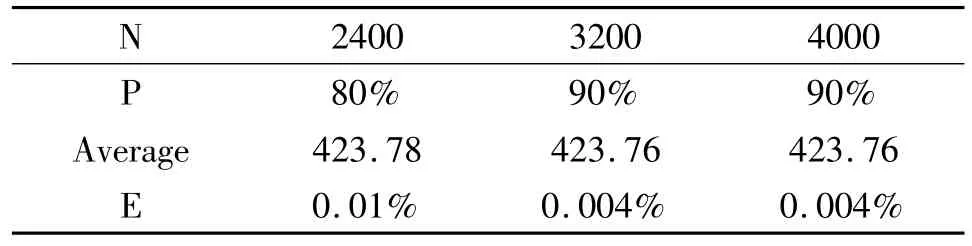
表3 DEDPSO多粒子群运算效果表

鉴于单纯的DPSO算法求解TSP问题容易陷入局部极值，而加入差分进化算法后，DPSO算法求解TSP问题的求解速度加快和求解质量提高，但是也不代表就得到了全局极值，本文还设置了多个粒子群进行并行搜索，提高了搜索到最优值的可能性。

设置了四个子种群进行并行搜索，四个子种群运行次数相同，分别为总运行次数的四分之一，且初始种群为200，缩放比例为0.1，交叉概率为0.6，同样还是采用标准的30个城市。依次运行2400次，3200次，4000次，对应的每个子种群也就是运行600次，800次，1000次，同时也分别运行基本的DPSO算法求解TSP问题2400次，3200次，4000次。得到的数据分别记录下来，表2为多粒子群DPSO算法运算效果表，表3为多粒子群DEDPSO算法运算效果表。表2和表3中P为每十次运行得到最优值的概率，Average为十次运行的平均值，E为平均值与最优值相比所存在的误差。

对比分析表2和表3：搜索次数均在2400次以上。运行2400次时，P等于20%，即每次有20%的可能性搜索到最优结果。运行3200次P等于40%。运行4000次P等于20%。可以看出随着程序运行次数的增加，基本的DPSO算法求解TSP问题寻优能力没什么突破，并且很不稳定，陷入局部极值的可能性很大。表3中的搜索次数也是2400次以上，即单个子种群运行次数在600次以上。运行2400次时，P等于80%，运行2600次时，P等于90%，运行4000次时，P等于90%，即运行次数在3200次以上，基本每次都能搜索到最优值。

这种基于差分进化的离散粒子群算法求解TSP问题充分利用了变异算子和交叉算子可以加快收敛速度的优势，提高了算法的整体寻优能力。

5 结束语

基于差分进化的离散粒子群算法的应用前景：文中提出的这种算法已经成功应用到了求解TSP问题上，并取得了较好结果；这种算法也可以应用到更大规模的TSP问题上以及类似的各种求解TSP问题的方法中，具体应用方式和对相应算法的改进有待进一步研究。

［1］王东，吴湘滨，毛先成，等.一种改进的求解TSP混合粒子群优化算法［J］.计算机工程，2008，34（6）：185-187.

［2］邓伟林，胡桂武.一种求旅行商问题的离散粒子群算法［J］.计算机与现代化，2012（3）：1-4.

［3］Eberhart R C，Kennedy J.A new optimizer using particles swarm theory［C］.Proceedings of the Sixth International Symposium on Micro Machine and Human Science.Nagoya：IEEE Inc，1995：39-43.

［4］Kennedy J，Eberhart R.A discrete binary version of the particle swarm algorithm.Proceedings of the World Multi-conference on Systemics［J］.Cybernetics and Informatics.Piscataway，NJ：IEEE Service Center，1997，4104-4109.

［5］高尚，韩斌，吴小俊，等.求解旅行商问题的混合粒子群优化算法［J］.控制与决策，2004，19（11）：1286-1289.

［6］Clerc M.Discrete particle swarm optimization-illustrated by the traveling salesman problem［EB／OL］.2000-02-29.http：／／clerc.maurice.free.fr／pso／pso_tsp／Discrete_ PSO_TSP.htm.

［7］Storn R，Price K.Differential evolution-A simple and efficient adaptive scheme for global optimization over continuous space［R］.International Computer Science Institute，Berkley，1995.

［8］杨妍，陈如清，俞金寿.差分进化粒子群混合优化算法的研究与应用［J］.计算机工程与应用，2010，46（25）：238-241.

［9］池元成，方杰，蔡国飙.基于差分进化和粒子群优化算法的混合优化算法［J］.计算机工程与设计，2009，30（12）：2963-2965.

［10］杨启文，蔡亮，薛云灿.差分进化算法综述［J］.模式识别与人工智能，2008，21（4）：506-513.

Discrete Particle Swarm Optim ization Algorithm Based on Differential Evolution for TSP

FU Cong，SHAWei，ZHANG Hai-xia，YANG Ya
（College of Internet of Things Engineering，Hohai University，Changzhou 213022，China）

Combining with the advantage of discrete particle swarm optimization（DPSO）and differential evolution（DE），a discrete particle swarm optimization algorithm based on differential evolution（DEDPSO）is proposed for solving traveling salesman problem（TSP）.There are two steps，one is employing the differentialmutation and selection operators to produce a new population for effective variation，and the other is carrying out DPSO for local exploration by crossover and selection operations.In this paper，some cases from TSPLIB are tested，and the experiment results show that DEDPSO has good performance for solving TSP.

Optimization algorithm；Discrete particle swarm；Differential evolution；Traveling salesman problem

10.3969／j.issn.1002-2279.2014.03.009

TP301.6

：A

：1002-2279（2014）03-0030-03

付聪（1990-），男，江苏省盐城市人，硕士研究生，主研方向：智能优化与控制。

2014-03-03