基于数据挖掘的尘肺病建模与预测研究❋

张翰英，杨照峰

（1.平顶山市工业学校，平顶山467000；2.平顶山学院软件学院，平顶山467002）

基于数据挖掘的尘肺病建模与预测研究❋

张翰英1，杨照峰2

（1.平顶山市工业学校，平顶山467000；2.平顶山学院软件学院，平顶山467002）

为了提高尘肺病的预测准确性，针对尘肺病历史数据少、不确定的特点，采用多种数据挖掘技术进行建模，提出一种基于GM-BPNN的尘肺病组合预测模型。首先利用灰色模型GM（1，1）对尘肺病进行预测，然后采用BP神经网络对GM（1，1）预测结果进行修正，并采用遗传算法优化BP神经网络的初始权值和阈值，最后对1981～2006年的尘肺病例进行仿真测试。仿真结果表明GM-BPNN很好地解决了尘肺病预测过程中的小样本、非线性问题，相对于单一预测模型，提高了尘肺病的预测精度。

尘肺病；灰色模型；BP神经网络；遗传算法；仿真

1 引 言

尘肺病是一种危害严重的职业病。据统计，尘肺病发病率一直呈上升趋势，不仅危害工人身体健康，而且给国家带来了经济损失，因此对尘肺病未来发病状况进行有效预测，然后根据预测结果对尘肺病进行控制和管理，具有十分重要意义［1］。

当前尘肺病预测方法主要包括传统统计学方法和数据挖掘技术预测方法。传统统计学方法包括线性回归预测、时间序列、趋势外推法和指数平滑法等［2］，这些方法参数设置少，简单易实现，但它们均假设尘肺病变化趋势是一种线性变化，实际上尘肺病预测是一种不确定、非线性变化系统，因此它们难以建立准确的尘肺病预测模型，预测结果与实际要求有一定的差距［3］。数据挖掘技术预测方法是一种非线性预测方法，其包括支持向量机、专家系统、灰色模型、贝叶斯网络等［4-5］，这些非线性预测方法提高了尘肺病预测精度，但它们都存在各自不足，尘肺病预测精度有待进一步提高。如专家系统通用性差，没有学习能力；灰色模型对随机波动性较大的数据拟合效果较差；神经网络结构复杂、要求样本大，而尘肺病是一种小样本、非线性预测问题，因此在样本不足的情况下，神经网络易出现过拟合缺陷［5］。支持向量机训练时间长，速度慢，参数确定没有统一标准［6］。近年来，基于组合优化理论，一些学者提出组合模型来克服单一模型的不足，预测精度相应提高，在经济、水资源、粮食产量等领域得到了广泛应用［7-8］。但到目前为今，还没有学者将组合模型应用于尘肺病预测。

为了提高尘肺病预测，将遗传算法、神经网络、灰色模型等多种数据挖掘技术组合在一起，建立一种灰色遗传神经网络的尘肺病组合预测模型。首先利用灰色模型对尘肺病历史数据建模和预测，然后采用遗传算法优化BP神经网络对灰色模型的尘肺病预测结果进行修正，最后采用具体数据对建立的尘肺病预测模型性能进行验证。

2 关键概念概述

2.1 灰色模型

灰色模型可以将无序尘肺病数据变成有规律数据，然后建立相应的微分方程模型，从而预测尘肺病未来发展趋势。在诸多的灰色模型中，以灰色系统中单序列一阶线性微分方程模型GM（1，1）最为常用。

（1）设有原始数据序列x（0），n为数据个数。

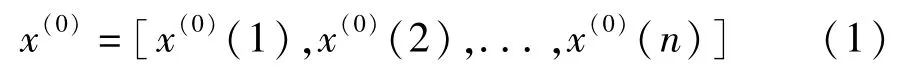
（2）对原始数据序列累加以便弱化随机序列的波动性和随机性，得到新数据序列：

（3）建立相应的微分方程模型为

式中，a为发展系数；u为灰色作用量。

只要求出参数a，u，就可以计算出x（1）（t），进一步可以得到x（0）的未来预测值。

（4）用累加生成数据构造累加矩阵B与常数项向量yn，即

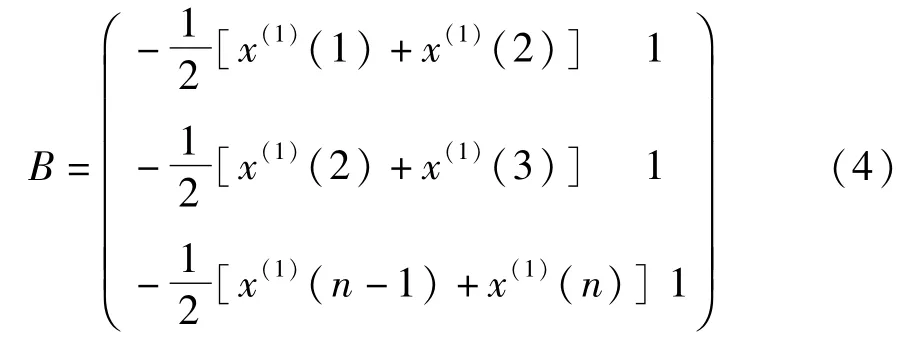
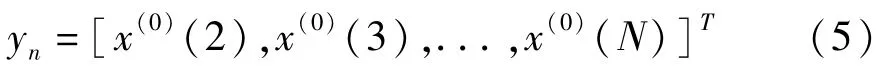
（5）用最小二乘法对灰参数求解

（6）该微分方程的解为

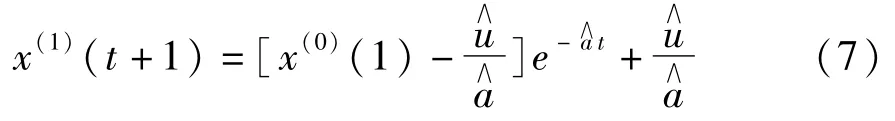
（7）累减还原得到

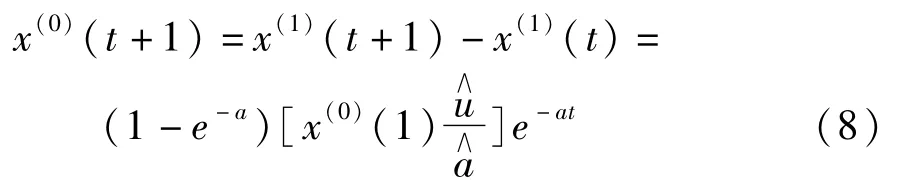
经过GM（1，1）对尘肺病预测后，捕捉到尘肺病总体变化规律，预测误差存在于预测值与原始值之间的残差中，因此采用BP神经网络对GM（1，1）预测残差进行修正，以提高尘肺病预测精度。

2.2 遗传算法优化的BP神经网络

遗传算法是美国密执安（Michigan）大学的John.H.Holland教授设计的一种借鉴生物界自然选择、遗传变异和进化机制的高度并行、随机、自适应的搜索算法，该算法具有简单易懂、鲁棒性强、适合并行处理的特点，可用于解决各种复杂优化问题。遗传算法对BP神经网络的优化主要用于得到最优网络初始权值和网络阈值［9］。遗传算法优化的BP神经网络算法流程如图1所示。经过遗传算法优化的BP神经网络能够获得更好的训练效果，提高预测精度。

图1 遗传算法优化的BP神经网络

3 GM-BPNN的预测模型构建

灰色模型适用于对近似指数增长、数据相对较少的数据序列进行预测，且灰色模型的累加生成不但能削弱原始数据存在的随机性，而且使累加后的序列单调增长，突出了总体发展趋势，适合用BPNN网络进行逼近，因此将BPNN和GM预测方法结合起来，使它们互相取长补短，构造性能更好的尘肺病预测组合模型是可行的。根据以上分析，本研究只保留灰色预测方法中的＂累加生成”和“累减还原”运算，不再求参数a和u。利用GM-BPNN对尘肺病进行预测过程如下：

（1）收集尘肺病历史数据。

（2）对尘肺病历数据进行灰色累加，生成累加序列

（3）采用归一化方法对生成的数据进行缩放，将它们变换到［0，1］之间，具体归一化公式为

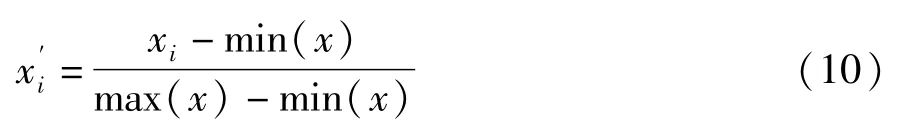
（4）建立尘肺病的GM（1，1）预测模型，并对测试样本进行预测。

（5）将GM（1，1）预测值进行“累减还原”运算，得到尘肺病预测值。

（6）计算GM（1，1）预测值与实际尘肺病值间残差，并对残差进行重构，得到BP神经网络的训练和测试样本。

（7）将残差训练样本输入到BPNN网络训练，并通过遗传算法优化其参数，建立尘肺病残差预测模型。

（8）根据建立的尘肺病残差预测模型对测试样本残差进行预测。

（9）将BPNN的预测结果与GM（1，1）的预测结果相加，得到尘肺病最终值。

4 仿真实验

4.1 数据来源

为了检验GM-BPNN对尘肺病预测的有效性，采用1981～2006年潞安矿区尘肺病例数据进行仿真实验，具体如表1所示。将数据分成为两部分：1981～2000年为训练样本，用于训练建立尘肺病预测模型，2001～2006年为测试样本，用于检验模型的有效性。

4.2 灰色模型拟合结果

将1981～2000年为训练样本输入到GM（1，1）中，采用Matlab 2007编写程序，建立GM（1，1）的尘肺病预测模型，然后对训练样本进行拟合，得到的拟合结果如图2所示。从图2可知，GM（1，1）对1981～2000年尘肺病例拟合精度为95.45%，拟合误差较大。可以把尘肺病总体变化趋势进行拟合，然后采用BP神经网络对GM（1，1）拟合残差进行校正，进一步挖掘尘肺病细节变化规律。

表1 1981～2006潞安矿区尘肺病例

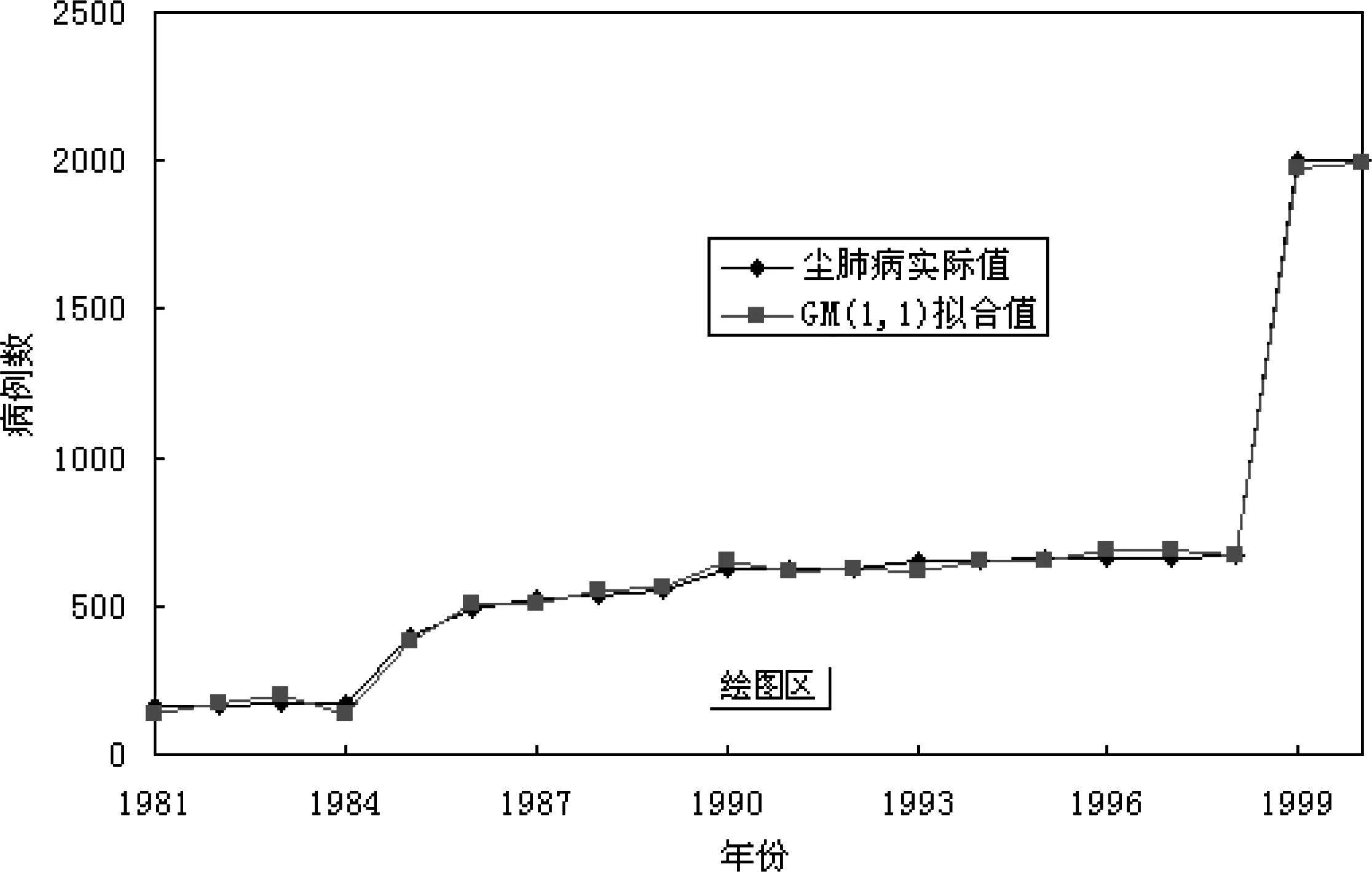
图2 GM（1，1）对1981～2000年尘肺病例的拟合效果

4.3 BP神经网络对GM（1，1）拟合残差进行修正

由于BP神经网络要求数据多维，不能对一维GM（1，1）残差时间序列进行直接建模，因此首先采用逐步增加维数方法选择GM（1，1）尘肺病拟合残差的维数，最后选择最佳维数为3，表示尘肺病例与前4年的尘肺病发生率相关，重构BP神经网络的尘肺病残差样本。将训练样本的残差输入到BP神经网络进行学习，采用遗传算法对BP神经网络初始权值和阈值进行优化，遗传算法的平均适应度函数值变化过程如图3所示。

BP神经网络的结构为：输入节点数为3，隐含层节点数为7，输出层节点数为1。采用优化后BP神经网络对训练样本的残差进行学习，然后进行拟合，最后采用BP神经网络对GM（1，1）的拟合结果进行修正，得到结果如图4所示。

从图4中知，相对于单一GM（1，1），GMBPNN的尘肺病拟合精度为99.54%，远远高于GM（1，1）。同时采用单一的BPNN对尘肺病训练样本进行训练和拟合，得到的拟合结果如图5所示。

图3 BP神经网络参数优化的适应度值变化过程

图4 GM-BPNN对1981～2000年尘肺病例的拟合效果

图5 BPNN对1981～2000年尘肺病例的拟合效果

从图5可知，单一BPNN对尘肺病拟合精度也不高，拟合精度为96.48%，难以准确、全面描述尘肺病的发生变化规律。各种模型的拟合结果对比表明，单一GM（1，1）或BPNN仅能反映尘肺病发生的部分信息，而GM-BPNN利用了GM（1，1）和BPNN优势，克服各自不足，对尘肺病发生规律进行深入、充分挖掘，有效降低了尘肺病拟合误差，初步证明GM-BPNN是一种有效的尘肺病预测模型。

4.4 模型的泛化能力比较

对于一个预测模型来说，其性能的优劣主要通过泛化能力来衡量。为此，采用GM（1，1）、BPNN作为模型，对测试样本进行预测，模型的评价标准为均方根误差（RMSE）和平均绝对相对误差（MAPE），它们分别定义如下：

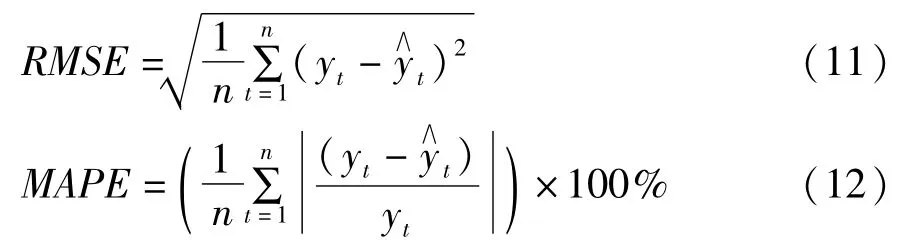
式中，yt为尘肺病例实际值，为模型预测值。

GM（1，1）、BPNN、GM-BPNN预测结果的RMSE和MAPE如表2所示。根据表2中的3种模型检验结果可知，对于小样本尘肺病例数据，GM-BPNN可以获得较高的预测精度，而单一GM（1，1）、BPNN预测结果不理想。综合上述可知，无论拟合能力或泛化能力，GM-BPNN均要优于单一预测模型，其预测结果更加可靠、客观，为国家管理和控制尘肺病提供科学依据。

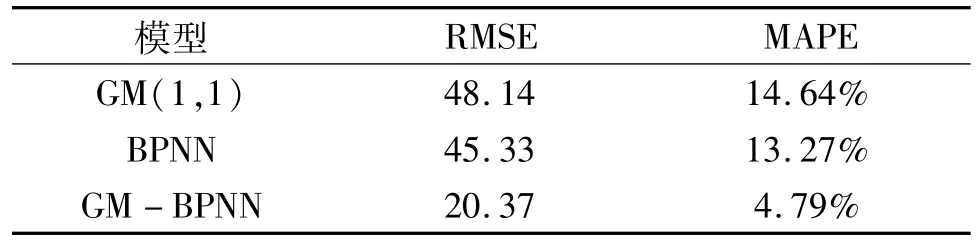
表2 几种尘肺病预测模型的综合性能对比

5 结束语

建立了一种基于GM-BPNN的尘肺病预测模型。仿真结果表明，GM-BPNN的拟合精度高，预测误差小，适合对我国尘肺病的预测研究。

［1］叶丽芳，朱玮.锡山市尘肺病发病趋势的观察与分析［J］.中国工业医学杂志，2004，10（2）：90-98.

［2］卢国栋，周心权.矿山企业尘肺病预测研究［J］.矿业安全与环保，2006，33（4）：12-14.

［3］谭希文.矿山企业尘肺病灰色残差预测模型研究［J］.矿业快报，2008（10）：51-53.

［4］郑双忠.基于神经网络的尘肺病预测模型研究［J］.中国安全生产科学技术，2005，6（1）：78-81.

［5］李舒才，肖全华，曹永兴，等.GM（1，1）灰色模型在尘肺患病人数预测的应用与评价［J］.预防医学，2004，18（10）：70-73.

［6］柳静献，刘铁民.尘肺危害的神经网络评价及预测研究［J］.中国安全科学学报，2001，11（2）：18-21.

［7］陈雄山，姚海飞，李东.基于灰色系统模型的潞安矿区尘肺病发病趋势预测［J］.中国煤炭，2011，37（2）：96-99.

［8］常杰，杭小平，魏彩娥等.尘肺病相关致病因素及防治对策的调查研究［J］.中国卫生工程学，2008，7（1）：100-103.

［9］刘全，王晓燕，傅启明，等.双精英协同进化遗传算法［J］.软件学报，2012，23（4）：765-775.

Study on Modeling and Prediction of Dust-pulmonary Disease based on GM-BPNN

ZHANG Han-ying1，YANG Zhao-feng2
（1.Pingdingshan Technical School，Pingdingshan 467000，China；2.School of Software Engineering，Pingdingshan University，Pingdingshan 467002，China）

Aiming at the problem of fewer historical data with uncertainty characteristics，in order to improve the accuracy of prediction for dust-pulmonary disease，the paper proposes one predictionmodel based on the GM-BPNN by usingmany datamining technology.Firstly，GM（1，1）is used to predict the dust-pulmonary disease，and then BP neural network is used to modify the prediction results of GM（1，1）which initial weights and thresholds of the BP neural network are optimized by genetic algorithm，and finally the test for dust-pulmonary disease case from 1981 to 2006 is conducted.The simulation results show that GM-BPNN is a good solution to the problems of small sample and nonlinear and the proposed model improves the precision of prediction for dust-pulmonary disease.

Dust-pulmonary disease；Greymodel；BP neural network；Genetic algorithm；Simulation

10.3969／j.issn.1002-2279.2014.03.015

TP183

：A

：1002-2279（2014）03-0052-04

河南省科技计划重点项目（102102210416）

张翰英（1979-），男，河南平顶山人，讲师，主研方向：从事计算机及网络技术应用方面的研究。

2013-10-25