CSNS直线加速器空间电荷效应的模拟研究
2014-08-07苑尧硕姚泽恩
袁 月,王 生,彭 军,苑尧硕,姚泽恩
(1.兰州大学 核科学与技术学院,甘肃 兰州 730000;
2.中国科学院 高能物理研究所,北京 100049)
中国散裂中子源(CSNS)是基于强流质子加速器的大型多学科实验装置,由一台81 MeV的H-注入器通过剥离注入为1.6 GeV的快循环质子同步加速器提供注入束流,该注入器由前端加速器和漂移管型直线加速器(DTL)组成。前端加速器包括50 keV潘宁H-离子源、低能束流输运线(LEBT)、3 MeV射频四极加速器(RFQ)、中能束流输运线(MEBT),漂移管型直线加速器将束流从3 MeV加速到81 MeV[1]。CSNS一期的设计束流功率为100 kW,并保留未来升级到500 kW束流功率的能力,与之相对应的直线加速器(LINAC)的设计峰值流强分别为15 mA和30 mA。在强流直线加速器中,束流的空间电荷效应是一非常重要的研究课题,其不仅会对线性磁聚焦系统造成扰动,同时具有很强的非线性效应,使束流电荷密度非均匀化,导致发射度增长,并形成低密度的束晕,造成束流损失,使加速器设备产生感生放射性[2]。大量带电粒子间的相互作用十分复杂,多粒子追踪程序为探索空间电荷效应的影响提供了一非常有效的手段。本文采用三维空间电荷效应模拟程序IMPACT-Z[3]模拟研究MEBT和DTL中空间电荷效应的影响,并同时考虑束流失配及误差效应对空间电荷效应的影响。
1 空间电荷效应模拟
分别采用三维空间电荷模拟程序IMPACT-Z和二维空间电荷模拟程序PARMILA[4],对流强为15 mA的束流从RFQ出口到DTL出口进行了模拟。程序IMPACT-Z计算三维空间电荷效应的网格划分数为32×32×32,程序PARMIALA计算二维空间电荷效应的网格划分数为40×80[5]。图1示出了两个程序计算的束流在水平、垂直、纵向3个方向的均方根发射度的对比结果。由图1可看出,两个程序计算得出的水平与纵向的发射度增长趋势一致,由于在MEBT部分有两个聚束腔,束流在聚束过程中纵向相宽变得较大,因此纵向发射度曲线有两个突起。两个程序对垂直方向束流发射度的模拟结果差别相对较大,最大偏离为10%左右,由于导致发射度增长的主要原因是空间电荷效应,而两个程序对空间电荷效应处理的不同导致了模拟结果中产生了较大的差别。下面的模拟研究中所采用的程序均为IMPACT-Z,该程序对空间电荷效应采用的是三维模型,模拟结果更接近实际情况。
2 DTL中空间电荷效应的模拟
CSNS中DTL由4个加速腔组成,共有156个加速单元,腔与腔之间的长度设计保持了纵向连续性。横向采用FFDD的磁聚焦结构,各腔首尾的半漂移管处未放置四极磁铁,由于自身空间电荷力的作用,束流在此处相移会变小,但变化程度很小。因此,在整个DTL中的四极磁铁排布可近似看成周期聚焦结构。通过跟踪粒子在每个周期结构后的相空间位置,可从微观上分析发射度的增长情况。
在直线加速器中,处于均衡状态的束流在穿过聚焦结构时不会经历发射度增长。但在现实中的加速器中,束流很难达到严格的均衡。在强流直线加速器中,空间电荷力的非线性作用是导致束流均方根发射度增长的主要原因。由空间电荷效应造成发射度增长的机制已有4种被证实[6]:束团电荷密度向均衡状态演化(当束流被加速时变化缓慢)、注入失配导致的包络振荡、横向与纵向的耦合共振、周期聚焦结构激励的共振。
1) 不同流强下发射度的增长
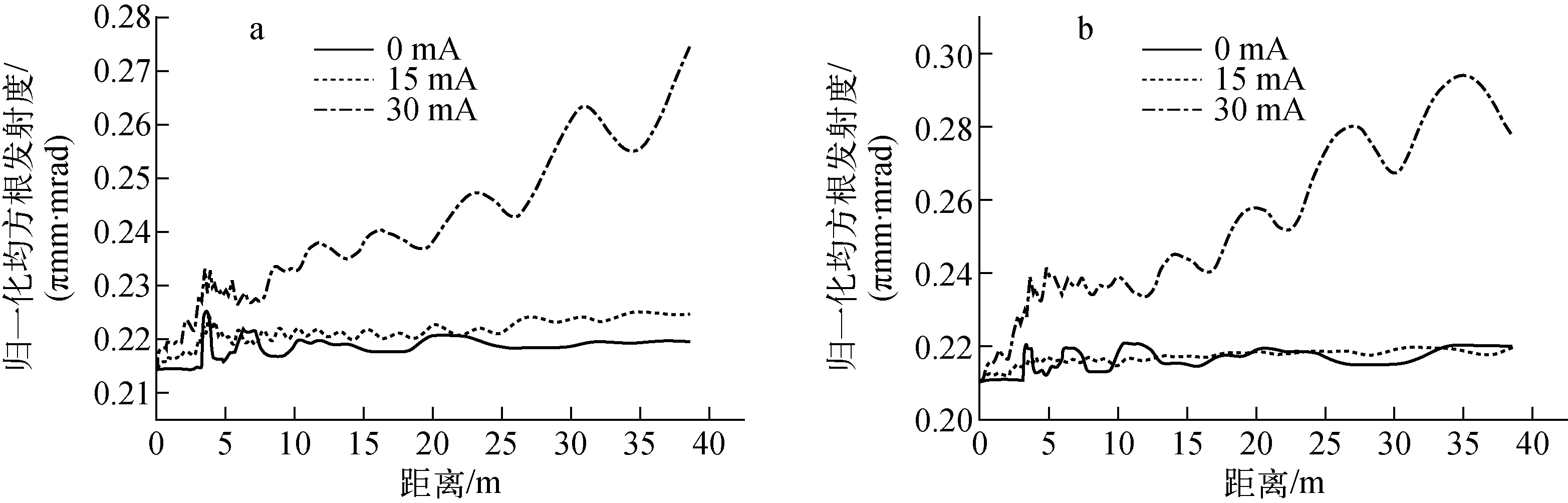
在模拟中,初始粒子分布采用6D水袋分布,宏粒子数为100 000。分别对0、15、30 mA 3种流强的束流进行了模拟,图2为不同流强下束流沿LINAC水平和垂直方向的发射度的比较。
由图2可知,在15 mA流强下,束流的均方根发射度增长很小,发射度的振荡逐渐趋于平缓。当流强达到30 mA时,发射度增长明显,增长比例约为30%。在严格周期聚焦结构中,若不考虑空间电荷效应的影响,单个粒子以每个周期为单位,在其横向相空间中的轨迹为一椭圆。由于DTL中粒子受到加速,实际的聚焦结构是一准周期聚焦结构,因此在不考虑空间电荷效应的情况下,粒子在横向相空间的轨迹应为一近似的椭圆。

a——水平方向;b——垂直方向;c——纵向
a——水平方向;b——垂直方向
以水平方向为例,将粒子的水平位置x与水平散角x′分别用c/ω和m0c进行归一化,其中c、ω、m0分别为真空光速、束团频率、粒子的静止质量。在0、15、30 mA流强下,从束核到束团边缘按发射度的大小依次选择3个粒子,记录这些粒子在DTL中每个FFDD聚焦周期结构后的相空间位置。图3为选定的3个粒子在3种流强下相空间位置的变化。可看出,由于DTL中的磁铁排列并非严格的周期结构,因此在零流强时,单个粒子在相空间的轨迹仅大致维持椭圆。当流强增大时,粒子间空间电荷力的排斥作用增强,单个粒子在相空间的椭圆轨迹增大,尤其对于束核粒子,其变化更为明显。由于非线性空间电荷力的作用,随束流在DTL中的传输和加速,压缩的束团倾向于逐渐演化为一密度相对减小的束核和周围低密度分布的其他粒子。因此,位于束核部分的粒子随流强的增加,相应的相空间轨迹变化最为明显,空间电荷效应导致了束核粒子发射度的显著变化。
2) 失配对束流的影响
在现实中的加速器中,聚焦结构的变化和注入条件的不匹配均会使束流与传输结构之间产生失配,从而导致束流包络的振荡,通常会激励起本征模的叠加。当某些粒子的振荡频率与包络模的振荡频率满足1∶2的条件时,便会形成参数共振,当这些粒子共振幅度增大时可能会从束核部分被踢到束团最外面形成束晕粒子,导致发射度的增长[7]。在模拟研究中,束流3个方向的初始失配因子[8]设为1.3,流强分别为0、15、30 mA,初始束流分布和粒子数与上述相同。图4示出了不同流强下束流横向归一化均方根发射度的增长情况,与图2相比,流强为30 mA时束流发射度的增长更明显,空间电荷效应对束流的影响增大,而流强为15 mA时,束流发射度增长相对不明显。
为进一步比较不同失配情况下空间电荷效应对束流的影响,以15 mA流强为例,分别对初始失配因子为1.1、1.3、1.4、1.5时的束流进行模拟,当失配因子增大到1.5时,在模拟过程中发现有3个粒子丢失在DTL第3个加速腔中,粒子丢失率为0.003%。图5为束流在DTL中横向最大包络的变化及其与漂移管孔径的比较,可看出,束流在第1、3个加速腔内垂直方向的最大包络已达到漂移管孔径限值。因此,应尽可能减小束流的初始失配因子,以免造成更多的粒子丢失。图6为不同失配情况下,束流均方根发射度与99%发射度的变化,当失配因子达1.5时,束流的发射度显著增长,均方根发射度增长约40%,99%发射度增长达3倍。图7为DTL入口与出口处束流相空间在垂直方向的投影(y和y′按上述方法进行了归一化,下同),可看出,DTL出口处的束流在垂直相空间的分布已出现严重的丝化现象,从而造成束流99%发射度的大幅增长。

a——束核;b——束团中部;c——束团边缘

a——水平方向;b——垂直方向
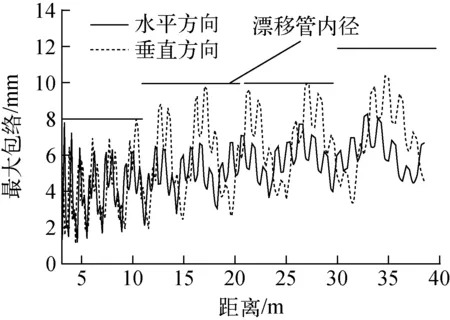
图5 失配因子为1.5时束流的最大包络
追踪指定粒子在DTL中相空间轨迹的变化,可从微观上看出发射度的变化。本文分别选择束核部分的5个粒子和束团边缘的5个粒子,观察这些粒子在不同初始失配因子情况下垂直相空间轨迹的变化。在束流匹配时,束核部分的5个粒子在DTL入口处垂直相空间的初始坐标分别为:(0.397 268 7×10-3,0.375 315 0×10-4)、(0.154 406 4×10-3,0.106 314 1×10-3)、(0.381 325 0×10-3,0.759 030 2×10-4)、(0.201 024 1×10-3,0.534 769 6×10-4)、(0.723 791 4×10-4,0.444 377 3×10-4),束团边缘5个粒子在相应位置的相空间坐标分别为:(0.109 321 4×10-1,0.963 975 2×10-3)、(-0.108 110 1×10-1,-0.918 372 4×10-3)、(0.905 736 1×10-2,0.120 461 2×10-2)、(-0.971 574 9×10-2,-0.122 540 2×10-2)、(0.114 674 6×10-1,0.533 241 7×10-3)。图8为初始束流匹配情况下,选定的束核内粒子在DTL每个聚焦周期结构后的垂直相空间轨迹,图9为束核内粒子在束流失配情况下对应的相空间轨迹。

图6 不同失配因子下束流垂直方向的发射度
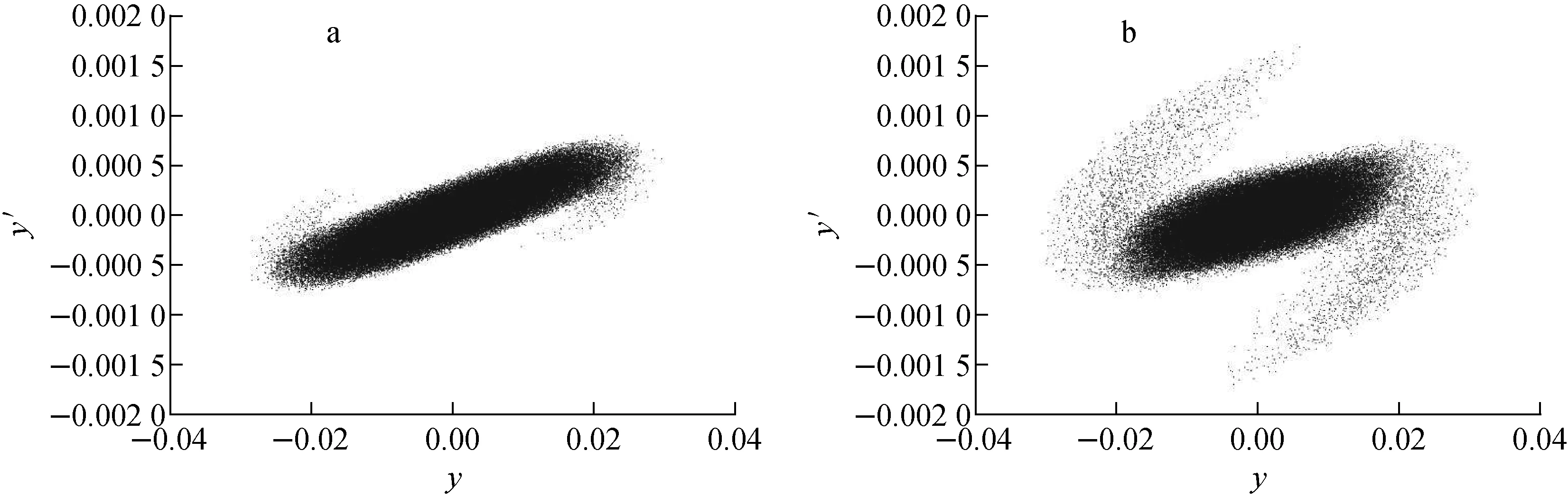
a——DTL入口;b——DTL出口
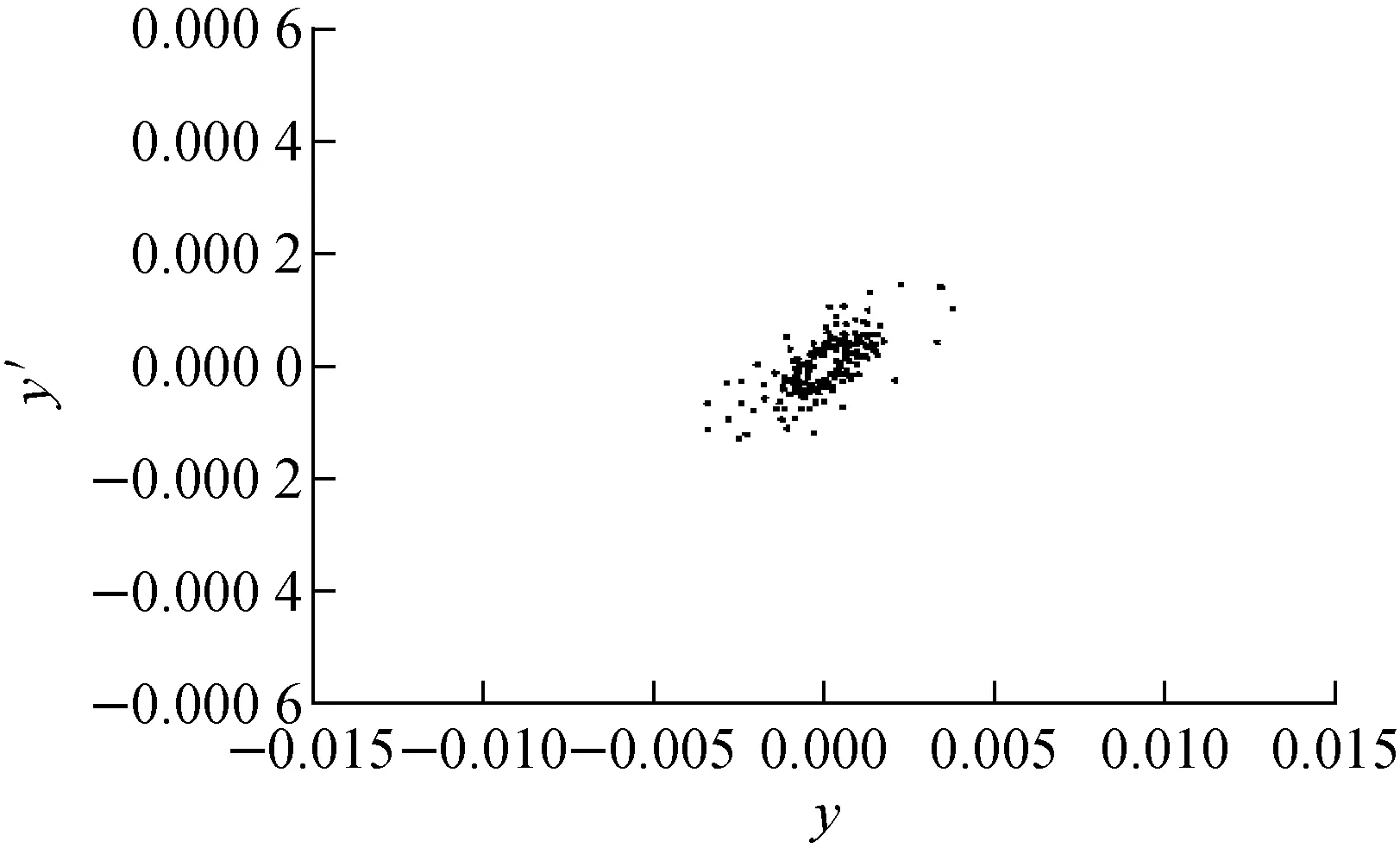
图8 束流匹配时束核内粒子相空间的变化

图9 不同失配因子下束核内粒子相空间的变化
从图9可看出,当初始束流的失配因子从1.1增大至1.4时,束核内粒子在垂直相空间的轨迹变化并不明显,直到失配因子达1.5时,粒子的相空间轨迹明显变大,此时由于束流的均方根失配产生的包络振荡,使粒子得到多余的自由能,从而使轨迹演化为代表发射度更大的相椭圆。
同样条件下,观察束团边缘粒子在相空间中轨迹的变化。图10为初始束流匹配情况下,选定的束团边缘粒子在DTL每1个聚焦周期结构后的垂直相空间轨迹,图11为束团边缘粒子在束流失配情况下的相空间轨迹。
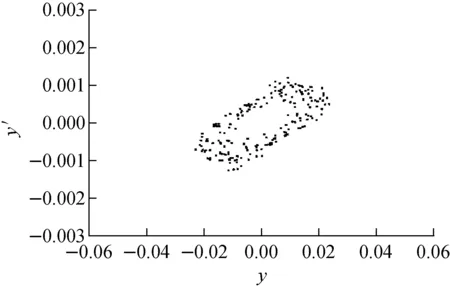
图10 束流匹配时束团边缘粒子相空间的变化
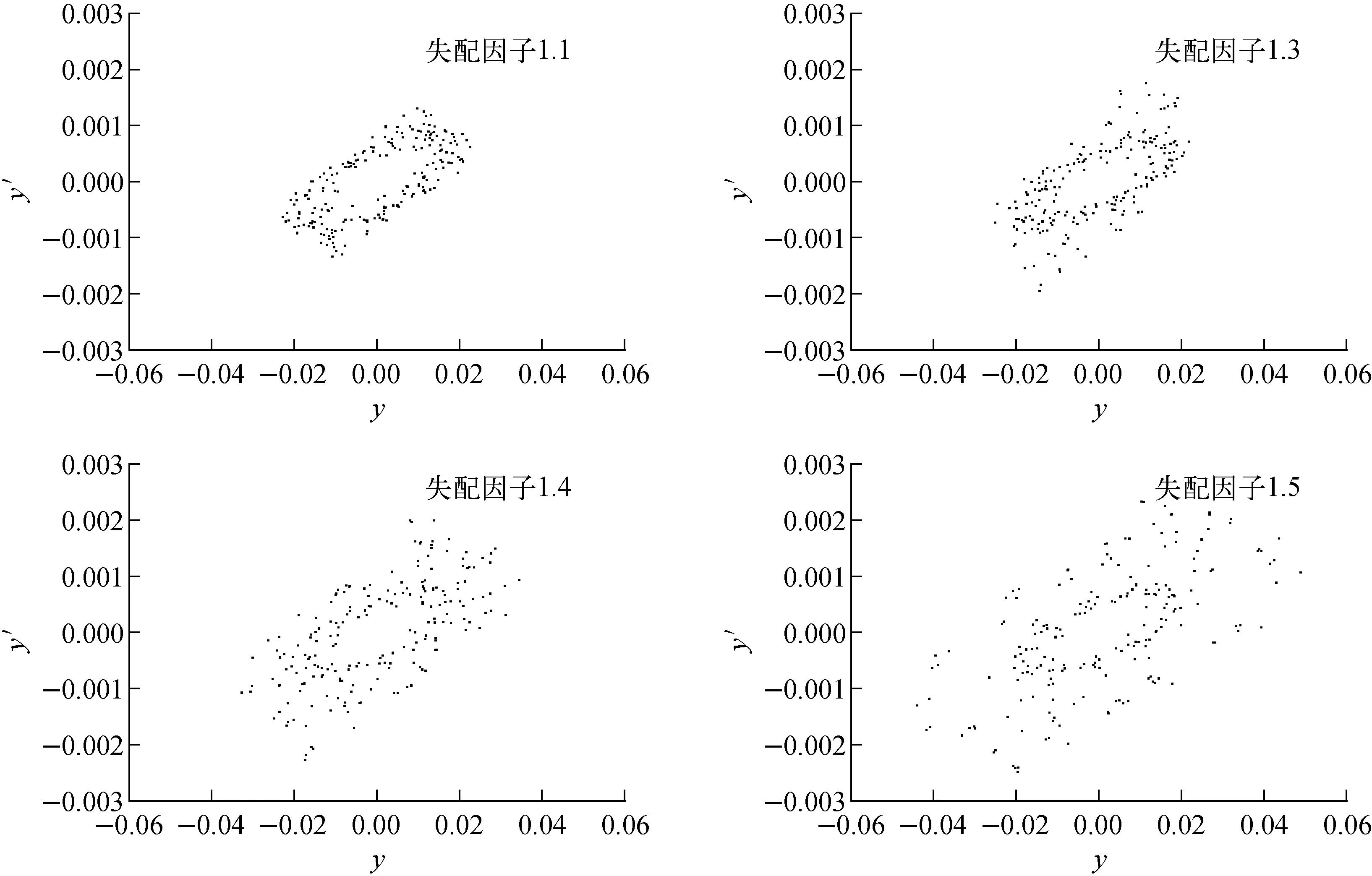
图11 不同失配因子下束团边缘粒子相空间的变化
上述模拟在束流的横向和纵向均引入了束流的初始失配,下面以垂直方向为例,比较横向和纵向失配对束流发射度的影响,结果如图12所示,其中失配因子均为1.5。从图12可看出,横向失配或纵向失配主要造成其对应方向的发射度增长。同时,束流对横向失配较纵向失配更加敏感,纵向失配时,束流的横向均方根发射度与纵向均方根发射度增长均很小,横向失配时,束流的横向均方根发射度增长较大,因此,在实际束流匹配时应优先考虑横向的匹配。
3 影响空间电荷效应的因素
理想的加速器不存在任何误差,而在实际的加速器中,设备加工和安装过程中总会存在误差,磁铁与高频场等存在的误差,影响到束流品质甚至造成束流损失,为了评估误差对束流品质的影响,利用程序IMPACT-Z进行了模拟研究。模拟中初始束流为6D水袋分布,流强15 mA,宏粒子数为100 000,在MEBT中不加误差,DTL中采用均匀分布的随机误差,每次模拟均采用10组误差进行计算,表1为模拟中使用的四极磁铁与高频场的静态误差。

a——垂直方向;b——纵向

表1 静态误差
3.1 磁铁与高频误差的影响
四极磁铁的设计梯度误差为1%,但考虑到磁测的精度,梯度误差在模拟中最大为3%,其他误差限不变。图13、14分别为四极磁铁梯度误差为1%、3%时,束流在DTL出口处横向发射度与无误差时的结果比较。在模拟中未发现束流损失,均方根发射度变化最大约为16%,99%发射度的变化较小,垂直方向较水平方向的发射度变化明显。

图13 DTL出口处束流横向发射度(磁铁梯度误差1%)
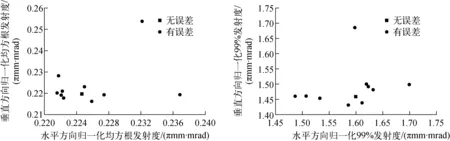
图14 DTL出口处束流横向发射度(磁铁梯度误差3%)
3.2 失配情况下误差的影响
由于RFQ出口处的束流通常与设计参数有较大差别,本文对束流3方向同时加上初始失配进行误差模拟,静态误差列于表1,磁铁梯度误差范围为1%,其他模拟参数与3.1节相同,初始失配因子分别为1.3、1.4、1.5。表2列出了不同失配因子时束流损失的百分比和束流损失的模拟次数。图15为误差模拟中束流在不同失配情况下的束流损失分布。束流损失主要位于DTL第3个加速腔内,在失配因子为1.5时,第2个加速腔内丢失1个粒子,因此应调节MEBT,尽量减小束流的初始失配。

表2 束流损失比例

图15 DTL中束流损失分布情况
4 总结
本文研究结果表明,在不考虑误差的情况下进行束流匹配时,横向失配对束流影响较大,应优先考虑横向匹配,束流的初始失配因子不应超过1.5。仅考虑静态误差时,模拟未发现有束流损失。综合考虑束流的初始失配与静态误差时,当失配因子达1.4时,发现有束流损失,且位于第3个加速腔内。当失配因子达1.5时束流损失增大,在第2、3个加速腔均有粒子丢失。因此,在实际调束过程中,应尽量减小DTL入口处的束流初始失配。
参考文献:
[1] WANG Sheng, FANG Shouxian, FU Shinian, et al. Introduction to the overall physics design of CSNS accelerators[J]. Chinese Physics C, 2009, 33(S2): 1-3.
[2] WANGLER T P. RF linear accelerators[M]. 2nd ed. America: Wiley-VCH Verlag GmbH & Co. KGaA, 2010: 283.
[3] QIANG J, RYNE R, HABIB S, et al. An object-oriented parallel particle-in-cell code for beam dynamics simulation in linear accelerators[J]. Journal of Computational Physics, 1999, 163(2): 55.
[4] SHISHLO A. Simulations for the SNS LINAC[C]∥Proceedings of HB2010. Morschach, Switzerland: [s.n.], 2010: 212-215.
[5] PENG Jun. Beam dynamics for CSNS LINAC[C]∥Proceedings of HB2012. Beijing: [s.n.], 2012: 24-30.
[6] WANGLER T P. High-brightness injectors for hadron colliders[R]. Hilton Head: Joint US-CERN School on Particle Accelerators, 1990.
[7] WANGLER T P, CRANDALL K R, RYNE R, et al. Particle-core model for transverse dynamics of beam halo[J]. Phys Rev ST Accel Beams, 1998, 1: 1-2.
[8] CRANDALL K R, RUSTHOI D P. Trace 3D documentation, LA-UR-97-886[R]. 3rd ed. New Mexico: LANL, 1997: 72-73.
