Cowell数值积分器的变步长与自起步方法

夏 炎, 田 波

(1.铜仁学院大数据学院，铜仁 554300；2.中国科学院紫金山天文台，南京 210008)

数值积分是一个经典问题，自20世纪70年代起，伴随着计算机技术的发展，对积分器的研究一直没有停止过。近几年仍不断有新的积分方法提出，计算高效、程序实现简单、适用性广是总的发展趋势[1-5]。积分器分为单步法和多步法，前者每步积分都需要计算多次被积函数，且步长较小；多步法积分器对被积函数的计算次数少，积分步长大，在计算效率上具有优势。

多步法积分器又分为等间距和可变间距。可变间距积分器可以灵活控制积分步长，但每积分一步都需要重新计算积分器系数，程序实现较为复杂[6]。而等间距的多步法积分器程序实现相对简单，使得它在人造卫星、自然天体的轨道计算中应用广泛[7-11]。然而在步长变换上一直都是难点，限制了其在大偏心率轨道、天体密近交汇等情况下的使用。如果可以为这类积分器解决变步长的困难，将对实际应用有很大帮助。

多步法积分器还有一个缺点就是积分器的起步比较复杂，需要在初始点附近求解多个点的状态后，才能启动正常积分。在实际应用中广泛使用的方法是求解各个步点的解析近似解然后迭代，或直接借助单步法积分器求解各步点再起步[6, 12-14]。如果可以摆脱对近似解或单步法积分器的依赖，将使积分器的使用更加方便和流畅。

自20世纪70年代起，紫金山天文台行星室就一直使用等间距的Cowell多步法积分器进行相关领域的研究[15-17]，在此过程中也对积分器本身提出了一些改进措施，文献[14]做过一次总结性的叙述。笔者在上述文献的基础上对Cowell积分器做了进一步改进。

首先推导了高阶的非整数步点坐标速度的求解系数，使得高精度计算非整数步点状态成为可能，以此为基础实现了积分步长的变换操作。随之而来的问题是变换步长的时机与步长大小的选取，提供了积分器截断误差的计算方法，可以以此为依据决定是否改变积分步长，以及预估步长改变之后的截断误差大小。利用二体问题模型对所给变步长方法做了检验，结果表明即便是几十万次的反复变步长操作也不会引入误差。

其次实现了积分器的逐阶迭代起步。逐阶迭代起步是理论上成熟的方法，但在实际应用中很少使用。其主要原因是其中要用到积分器每一阶的系数，而低阶积分器使用较少，其积分器系数也不易查到。给出了各阶积分器系数、算法流程与程序实例，方便参考使用。

最后介绍一种减小积分器舍入误差的措施，可以大幅减小积分器误差。有助于解决高精度的深空探测数据处理、超长期的行星系统演化问题。积分器精度优于以能量保持性占优的IAS15积分器[5]。

涉及的积分器系数以及相关算法的示例程序源代码已经上传到github网站[18-19]。

1 基本算法

需要求解的基本方程为

(1)

为了推导积分公式有以下算子：

移位算子Ef(t)=f(t+h)；

如文献[4]中的推导，算子之间存在如下关系：

E=ehD。

于是有：

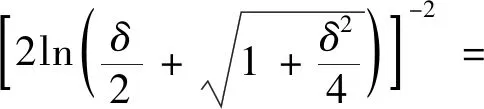
(2)

(3)

再根据中差算子的运算[14]就可以把坐标和速度的计算与已知步点的函数值联系起来。

(4)

如果函数表和和分表已知，那就可以根据式(2)和式(3)计算各步点的坐标速度，最终坐标的计算简化如下：

(5)

式(5)中：yk是第k个步点的坐标，k∈[-7,7]；U是一个8×13的常系数矩阵。速度的计算也有类似的公式，将在后文统一给出。

要进行一次积分运算，遵循如下流程：首先构建13个已知步点的函数值，使用较多的方法是用解析近似解，迭代至收敛；然后利用式(5)和初始坐标速度，以及式(4)，完成和分表；最后可以逐步外推，外推一步的流程如下。

(1)利用式(4)计算+7步点和分值。

(2)利用式(5)计算+7步点的坐标速度，进而计算函数值，称为预报。

(3)函数表、和分表移动一个步点。

(4)利用式(5)计算+6步点的坐标速度，进而计算函数值，称为修正。

2 变步长的实现

积分器改变步长就是重新构建13个已知点，并使它们之间的距离缩小或放大。首先给出非整数步点状态的高精度求解，用来计算任意时刻的被积函数，以此构建13个新步点，从而实现步长变换的操作；然后给出截断误差的计算，作为步长选取和变换时机的判据。

2.1 非整数步点坐标速度的计算

以往对于非整数步点状态的求解只是用来作为输出工具，其结果不参与积分迭代，要求的精度不高。文献[14]中推导了8阶的积分器，但非整数步点的计算精度只准确到了4阶。笔者针对12阶的积分器推导同样准确到12阶非整数步点的系数。

设实数n∈(-1,1)，则在整数步点k附近的k+n处有：

fk+n=Enfk=enhDfk=

(6)

使用(hD)-2作用在fk上即得整数步点的坐标，现在把它作用在fk+n上就可以得到非整数步点坐标的计算公式,即

(hD)-2fk+n=[(hD)-2+n(hD)-1+

(7)

然后类似于整数步点的处理，可以得到使用函数表计算坐标的方法，其中需要15个8×13的常系数矩阵，记为U15,8,13；最终对于步点k∈[-7,7]附近的位置k+n处，非整数步点的坐标计算公式如下：

当k≥0时，

(8)

当k≤0时，

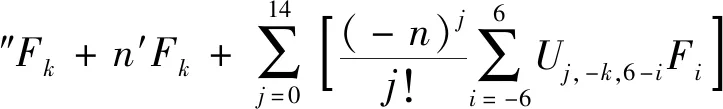
(9)

式中：

(10)

同样的方法可以得到速度计算公式。

当k≥0时，

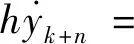
(11)

当k≤0时，

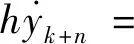
(12)

若n=0，则不需要再对j求和，只需要计算j取值最小的单项就可以了，也就回到了整数步点的计算公式。

2.2 变步长的操作

变步长的操作核心是按照新步长重新构建13个步点。在解决了非整数步点的坐标速度的求解问题之后，步长的缩小就是简单的。步长减半的操作如下。

(1)保存中心步点的坐标速度。

(2)计算-2.5、-1.5、-0.5、0.5、1.5、2.5步点处的坐标速度，再计算右函数，结合已知的-3到+3的整数步点的加速度，就构成了13个已知点。

(3)使用保存的中心步点坐标速度，根据式(5)确定和分表。

为了便于扩大步长，对传统的积分器使用方法做了一点改变，增加了保存的函数值的个数。传统方法只要保存13个步点的函数值，就可以使积分器外推。现在改为保存25个步点，这样就可以很方便地实现步长加倍的操作。而在今天的计算条件下，多保留的这些步点并不会造成计算负担。

对上述变步长方法进行了测试，使用日地二体模型，对地球轨道积分1 000圈，积分结果与二体模型解析结果比较，如图1所示。

图1 变步长对积分精度的影响Fig.1 The influence of change step size on precision

从图1中可以看出，变步长的操作不会引入额外误差，而造成精度损失。采用固定积分步长1、2、4 d做积分运算。对变步长做了两个测试：在1 d与2 d之间反复切换，和在2 d与4 d之间反复切换。步长为1 d和2 d之间切换时，增大步长365 249次，减半365 250次；步长为2 d和4 d之间切换时，增大步长182 624次，减半182 625次。从图1中可以看出，虽然有几十万次的变步长操作，但并未对计算精度造成影响。(计算中使用的变量类型是IEEE规范的双精度浮点数类型。)

2.3 变步长的判据

解决了积分器变步长的具体操作后，另一个问题是变步长的时机判断，在积分过程中怎样判断当前的积分步长是否合适，需要增大还是减小。

文献[6]中讨论了Gauss-Jackson积分器改变步长的判据，是使用预报值与改正值的差作为判据，理由是预报值比修正值少使用了一个步点，所以可以认为预报值精度低1阶。但Gauss-Jackson积分器是基于后差算子的，而在由中差算子导出的Cowell积分器中，没有明显的证据说预报值比修正值少使用了一个步点。所以使用预报值与修正值的差作为判据就有些牵强。

利用式(2)可以很严格地给出计算积分的12阶截断误差为5.104×10-7δ12，结合文献[4]对差分的计算，最终可以得到12阶截断误差的计算方法如下：

(13)

式(13)中：A是常系数数组，其值为{1，-12，66，-220，495，-792，924，-792，495，-220，66，-12，1}。

注意到式(13)中截断误差的计算只和函数表有关，而在上一节中，把函数表保留的步点增加了一倍，使得扩大步长的操作变得简便。在这里，这些多保留的步点也就可以用来预判扩大步长后的截断误差，即可以事先计算积分步长增大一倍后的截断误差会是多大，这有助于实际使用。

3 积分器的自起步

积分器要解决的是给定初始状态的常微分方程，已知状态只有一个时间点。但是要让多步法积分器开始工作，需要首先构建一系列的已知点，计算这些点的函数值，如12阶的积分器就需要13个这样的已知点，而为了求解这13个点的函数值，通常是借助积分器以外的工具。

第一种方法是求助于单步法积分器，该方法应用比较普遍[20]。另一种方法是为各个步点寻求近似解析解，然后迭代至给定精度。关于解析近似解的来源，有的采用二体模型下的解[12, 14]，有的使用级数展开方式考虑一定的摄动因素[6]。

无论是借助单步法积分器，还是借助解析近似解都让积分器欠缺单独工作的能力，在文献[21]中有针对2阶积分器的起步方法研究，但并不能推广到更高阶的情况。在此给出一种逐阶迭代的方式来实现积分器的自起步，具体流程如下。

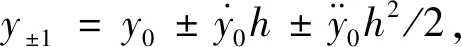
(3)把得到的3个点的函数值，作为2阶积分器的初始近似，迭代至收敛；然后向前向后各外推一个点，作为4阶积分器的初始近似，再迭代至收敛。

(4)类似前一步，从4阶到6阶，再到8阶……一直到12阶。

算法的实现需要用到由2阶至12阶，每隔两阶的所有积分器系数，系数推导方法如前文所述，具体系数矩阵可在示例源码中找到。

4 舍入误差的减小

如何减小积分器误差是个永恒的问题[22]。Al-Mohy等[23]讨论过浮点数求和的舍入误差问题，并给出了几种减小舍入误差的方法；Grazier等[24]把其中方法应用在了积分器上。紫金山天文台张家祥等长期从事数值计算研究[25]，针对Cowell积分器也提出过一种减小舍入误差的措施，简单有效，在科研工作中一直被使用，文献[14]中曾对此做过说明。笔者为了使阐述的积分器更加完善，也做一下介绍。

浮点数的大数和小数相加减会丢失小数的精度，特别的，积分器的外推是依照式(4)进行的，而其中的和分值″F和函数值F通常都有几个数量级的相差，它们的加减是积分器误差的主要来源，这个误差会引入迭代中去，而且每一步迭代又都有新的误差产生。

使用两个浮点数变量存储一个和分值的方法，以增加和分值存储的有效数字位数。具体的操作是让和分值乘以一个系数(记为Z)，使乘积的整数位具有一定的有效位数，然后把该乘积的整数部分和小数部分分别用两个变量存储。当有数值要与和分值做加法运算时，把该数值也乘以Z，然后整数与整数部分相加，小数与小数部分相加，并把小数部分产生的整数清除，加到整数部分里。

上述方法可以大幅提高积分器精度。对外太阳系天体做长期积分，考察其能量保持性，积分108个木星周期，能量差在10-13的量级，这个结果比以能量保持性占优的IAS15积分器[2]还要好。但是能量保持的精度并不代表积分器的精度[26]，所以仍然使用日地二体模型给出一个对比结果，如图2所示。

图2中纵轴是积分结果和解析解的位置误差，横轴是积分时间。可以看出增加字长措施大大减小了积分误差，使得积分109圈以后地球仍然保持了它大体的位置，精度在10-3。计算中使用的变量类型是IEEE规范的双精度浮点数，积分步长为1 d。

图2 增加和分存储字长的效果Fig.2 The effect of extending storage length of summations

5 结论

Cowell积分器简单易用、计算效率高，在天体力学中有着广泛的应用，但也存在着变步长困难、积分起步相对复杂的缺点。针对这些问题做了改进，并介绍了一些使积分器更加完善的措施。主要改进有以下几点。

(1)提供了高精度计算非整数步点状态的具体方法。如果没有非整数步点的计算，积分器在积分过程中就是一些离散的点，有了非整数步点的状态的计算，使得积分器更像是在时间轴上行进的一段连续函数。这对于处理某些问题，诸如光行时修正等，是非常便利的。

(2)提供了一种变换步长的方法，这种变步长方法不会引入额外的积分误差，并介绍了变步长的判据。积分器具备了变步长能力后，将大大拓展它的使用空间，例如深空探测中探测器飞掠大行星的问题，如果采用固定步长，将不得不整条轨道都采取很小的积分步长，徒增计算量。

(3)改进了积分器的起步流程，使得积分器可以单独工作，不需要借助于解析近似解或其他积分器起步。

(4)介绍了一种增加和分值存储字长的方法，该方法可以大幅减小舍入误差。使得二体模型下的被积天体在计算109圈后，仍然保持可信赖的位置精度。

对Cowell积分器的改进可为其他积分器提供参考。