对NOTRUMP-AP600程序缺少动量通量项的评估与修正

樊 普，郑尧瑶

(上海核工程研究设计院，上海 200233)

AP600核电厂为非能动核电厂，对于小破口事故，采用非能动堆芯冷却系统缓解事故，将电站带至安全状态。根据法规，新增的系统性能必须通过试验验证其可靠性，并为事故分析程序提供数据验证。西屋公司进行了单项试验和整体试验(APEX-600和SPES-2)验证其性能。在采用Oregon州立大学(OSU)整体实验台架的试验数据验证小破口事故分析程序NOTRUMP-AP600的过程中，发现第4级自动卸压系统(ADS4)触发后稳压器的排水性能未被正确模拟[1]，这将导致注入堆芯的水装量增加，分析结果不保守，需对此问题引起高度重视。

NRC在对NOTRUM-AP600程序评审时，确认导致这些现象的发生是源于NOTRUMP-AP600程序的动量守恒方程忽略了动量通量密度的散度项(简称动量通量项)。本工作将评估NOTRUMP-AP600程序忽略动量通量项的影响，并对此问题进行修正。

1 采用两相动量守恒方程对缺失动量通量项的评估

1.1 动量守恒方程

NOTRUMP-AP600程序中的动量守恒方程为：

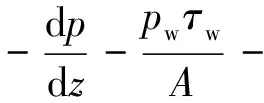
(1)

式中：G为混合物质量流速，kg/(m2·s)；um为混合物速度，m/s；A为流动面积，m2；ρ为密度，kg/m3；pw为壁面周长，m；p为压力，MPa；z为管路长度，m；g为重力加速度，m/s2；ur为液相和气相的相对速度，m/s；ρr为参考密度，其定义为ρr=ρfρgα(1-α)/ρm，kg/m3，α为空泡份额，下标f、g、m分别表示液相、气相和混合物；t为时间，s；τw为单位面积上的壁面剪切应力，N/m2。

该方程采用漂移流模型计算质量流量，当评估其缺失动量通量项影响时，需提供漂移流模型等复杂经验关联式，为此本文将分别采用均相流和分相流模型的动量守恒方程来评价动量通量项对动量守恒方程的影响。

一维混合物动量守恒方程为：

ρg

(2)

式中：G=(Wf+Wg)/A=ρf(1-α)uf+ρgαug；Wf为液相质量流量，Wf=ρf(1-α)ufA；Wg为气相质量流量，Wg=ρgαugA；uf和ug分别为液相和气相速度。

对于稳态工况：

(3)

W=常数

(4)

(5)

式中：ffanning为混合物的范宁摩擦系数；D为水力直径。

对于两相摩擦压降，式(5)可表示为：

(6)

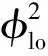
对于均相流模型，动量通量项为：

(7)

对于稳态均相流模型，动量守恒方程为：

ρg

(8)

对于稳态情况：

(9)

式中，υ为比容，υ=1/ρ。

可见，加速压降是由于两部分引起：混合物密度变化和面积变化。

对于均相流模型，混合物的比容υ可表示为：

υ=υf(1-x)+xυg

式中：x为质量含气率；υf为饱和液相比容；υg为饱和气相比容。

则：

(10)

式中，υfg=υg-υf。

在沸腾导致的换热或压力下降引起闪蒸时，含气率梯度将变得重要。假如沸腾占主导，则：

′

(11)

式中：h为焓；hfg为汽化潜热，hfg=hg-hf，hg为饱和气相焓，hf为饱和液相焓。

如果压力梯度导致含气率梯度占主导，则：

(12)

由式(12)可见，对于沿ADS管路压降变化导致的闪蒸，由于分母中包括了hfg，而汽化潜热较大，因此此项很小，可忽略。

综合式(8)～(11)得：

(13)

1.2 滑速比的影响

考虑气相和液相之间相对速度的影响，采用分相流模型推导压力梯度方程。对于分相流模型，动量通量项仍为式(2)中的项：

(14)

其中：

(15)

对于稳态，W为常数，则加速项变为：

(16)

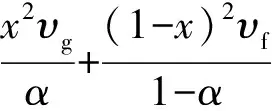
Sx(1-x)υf+(1-x)2υf

(17)

式中，若S=1，则式(17)等于xυg+υf(1-x)。

故式(16)可表示为：

υ+x(1-x)·

(18)

假设含气率沿轴向梯度很小(由于汽化潜热很大)，则式(13)中的分母为：

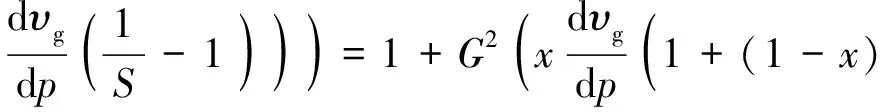
(19)

式中，υ=xυg+υf(1-x)。

若S=1，则式(19)即为式(13)右侧中的分母。

1.3 临界流模型

本文计算采用均匀平衡临界流模型，此模型假设如下：1) 气相和液相速度相等；2) 流体处于热力学平衡状态；3) 流动是稳态等熵。在均匀平衡临界流模型假定下，按等熵过程假定，根据能量守恒方程[2]得：

(20)

式中：hr为滞止焓(即流体速度为0时的焓)；ht为喉部处焓；ut为喉部处速度；J为单位转换因子。

根据假设3，流动为等熵流动，故：

Sr=St=Sf(pt)+xSfg(pt)

(21)

式中：pt为滞止压力；Sr为滞止熵(即流体速度为0时的熵)；St为喉部的熵；Sfg=Sg-Sf，Sf为饱和液相熵，Sg为饱和气相熵。

Gt为喉部处两相混合物的质量流速，Gt=ut/υt，υt为喉部处两相混合物比容，则有：

(22)

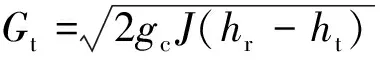
(23)

式中，gc为重力加速度。

喉部处的比容υt和焓为喉部压力pt的函数，即υt=f(pt)，ht=f(pt)。

将式(23)对压力求导得：

(24)

(25)

对式(25)可通过二分法迭代求解，即得到发生临界流处的压力，然后可求得发生临界流的质量流速。欲通过式(25)进行求解，还需给出滞止焓，本文中取值为根据压力和温度计算得到的焓，即忽略流体的动能。

1.4 动量通量项的评估

对于AP600的第1～3级ADS(ADS1～3)阀门，连接稳压器的管路面积为Apipe=0.063 4 m2，阀门的喉径面积为AAD13=0.030 1 m2。对于AP600的ADS4管路，连接热段的管路面积为Apipe=0.051 93 m2，2个ADS4管路阀门的喉径面积为AAD13=0.048 96 m2。可见，对ADS1～3，阀门面积是管路面积的1/2，所以当阀门处发生临界流时，管路中的质量流速相对较低。而对于ADS4，当2个阀门全部开启时，管路面积和阀门处面积相差不多，故在阀门处发生临界流时，管路内的质量流速也较高，将可能导致式(13)中的分母或式(22)远小于1的情况。

图1为对ADS1～3和ADS4管路系统计算得到的压力梯度方程中的分母项在不同压力下随含气率的变化。从图1可见，在高含气率下，此分母近似保持为常数，因此可对管路系统的阻力系数乘上1个因子。图2为对第ADS1～3和ADS4管路系统计算得到的管路中的两相混合物速度在不同压力下随含气率的变化。由图2可见，ADS4管路的速度远高于ADS1～3中的速度，因此式(13)分母中的G2项在ADS4管路中较ADS1～3管路大得多，因此，综合比容对压力梯度的影响，使动量守恒方程中忽略动量通量项在ADS4管路中的影响较在ADS1～3管路中的大得多。图3为0.344 MPa压力下滑速比对动量通量项的影响。从图3可见，滑速比等于1(即均相流模型)的工况，式(13)分母或式(19)的值更小一些，即采用均相流模型计算的压降更大一些，通过ADS4管路的流量降低，因此非能动核电厂的降压更为缓慢，从而使安全壳内置换料水箱(IRWST)开始注射的时间延迟，即结果更为保守。

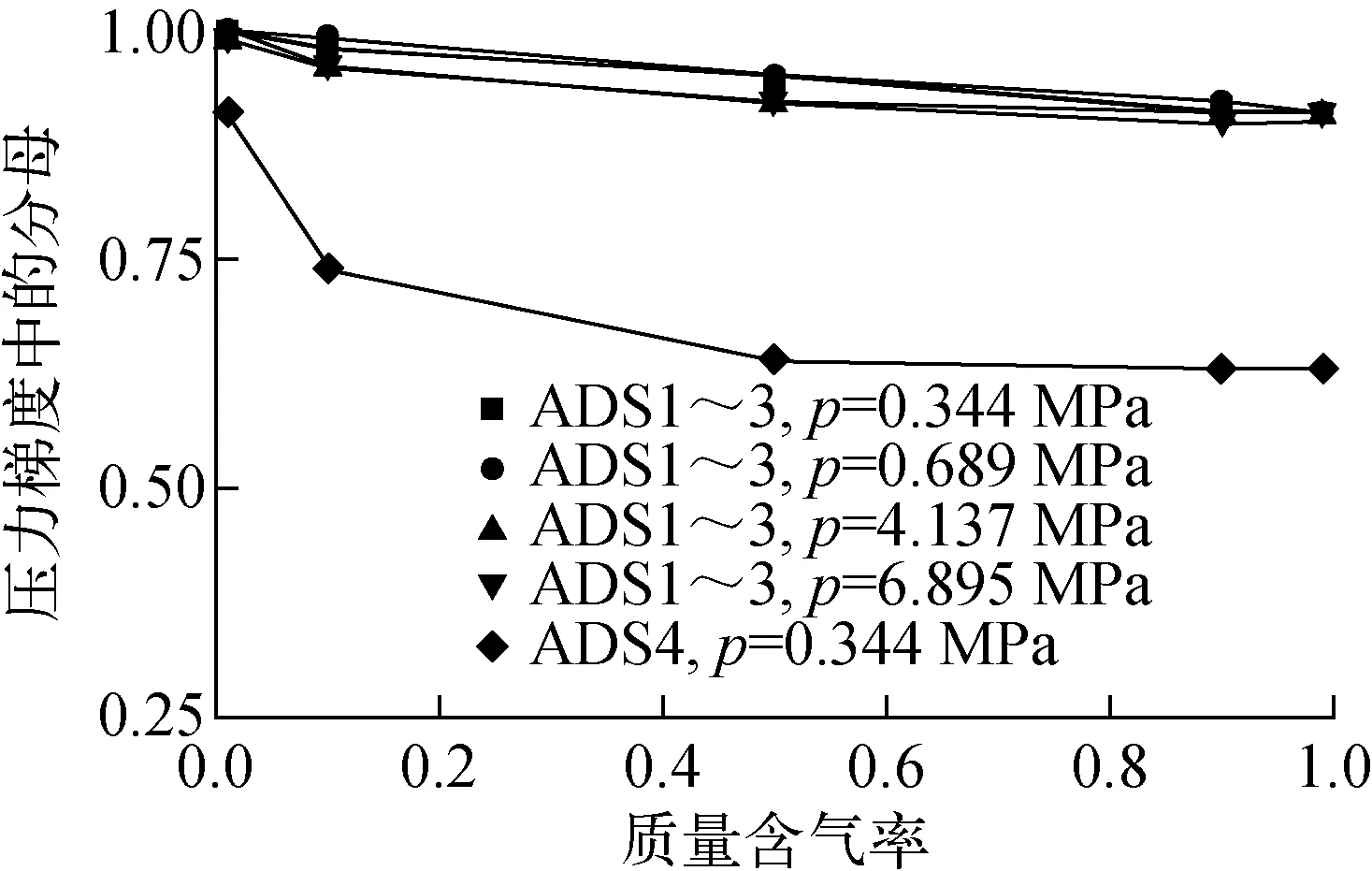
图1 不同压力下式(13)中分母随质量含气率的变化

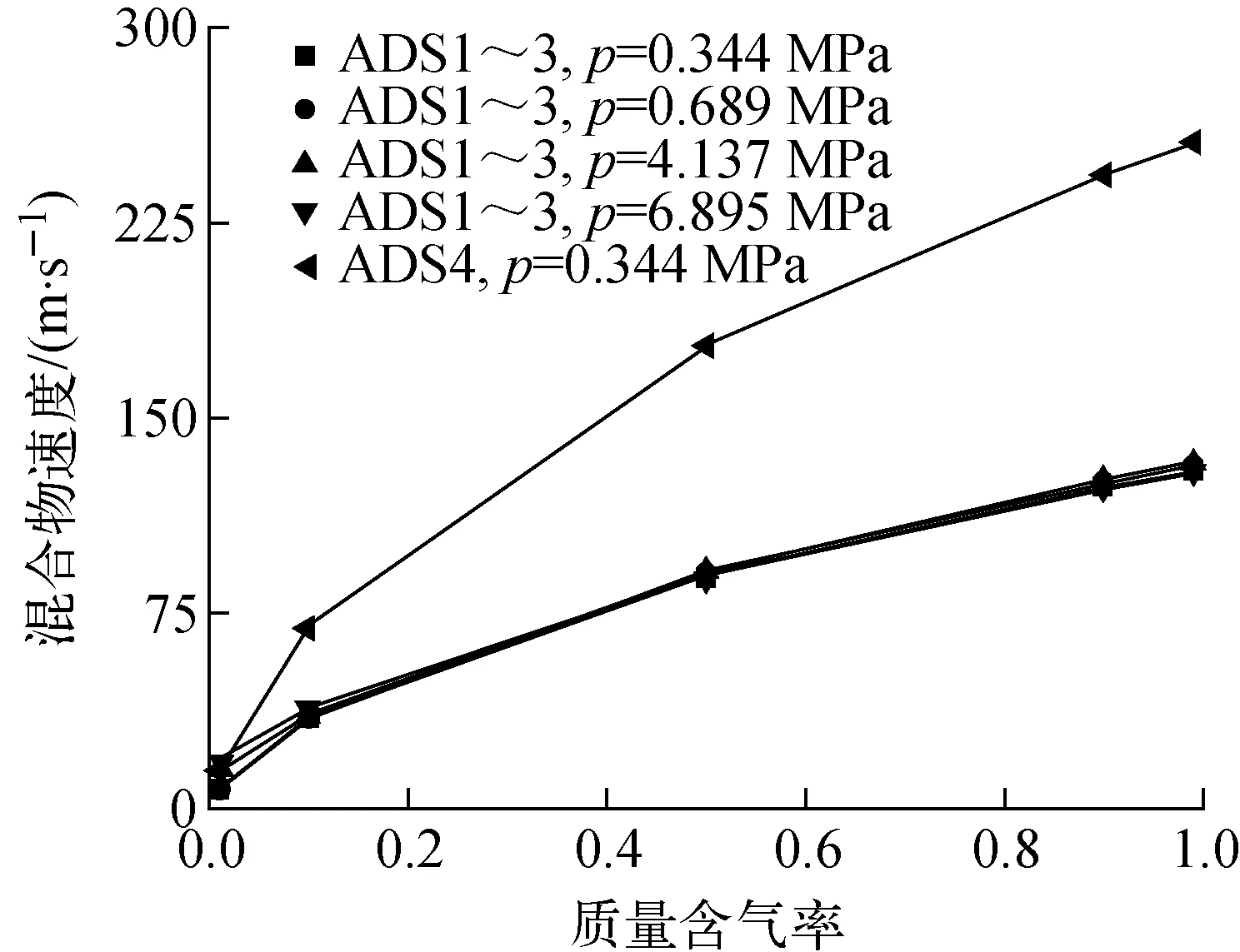
图2 不同压力下管路中两相混合物速度随质量含气率的变化

由以上分析可知，动量守恒方程中动量通量项的缺失将会引起ADS1～3和ADS4管路两相压降预测出现误差。对于ADS1～3管路，相对误差不超过10%，此误差范围是可接受的。而对于ADS4管路则相对误差较大，必须进行修正。

图3 0.344 MPa下滑速比对动量通量项的影响

2 ADS4管路模型

ADS4管路包括1个连接热段的管道，然后分成2个直径较小的管道，末端为2个爆破阀，爆破阀上游为闸阀。西屋公司开发了用于求解ADS4管路两相流压降的FLOAD4程序，可计算稳态下管路中的压力和含气率的分布(从热段到最后一个阀门)。前面的结果表明，均相流模型计算的压降较考虑气相与液相之间速度差的大，ADS4管路排放流量小，结果更为保守，故在FLOAD4程序中所用的两相压降模型为均相流模型。

2.1 FLOAD4程序中的ADS4管路模型

稳态绝热一维流动的能量守恒方程[2]为：

(26)

(27)

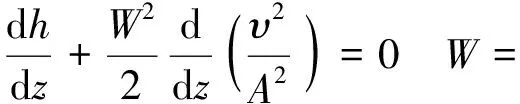
(28)

式中，υ=υf+xυfg，h=hf+xhfg，代入式(28)得：

(29)

(30)

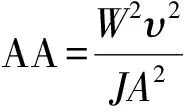
(31)

将式(31)代入式(13)并将单位转换得：

(32)

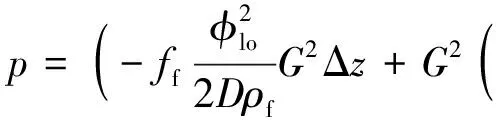
(33)

对式(33)积分得：

(34)

2.2 FLOAD4程序求解过程

FLOAD4程序通过对稳态的一维动量和能量守恒方程进行求解，得到ADS4管路内的压力和含气率，然后对式(25)采用迭代算法。计算每个爆破阀的管路流量，涉及的求解公式为式(33)和(34)。

3 ADS4管路计算分析

在得到ADS4管路的流量后，根据下式求ADS4管路的等效阻力系数：

Keff=2.0Δp/(υ(WADS4/AADS4)2)

(35)

对于每一热段处的压力和含气率，可求得一等效阻力系数Keff，并用相同含气率下压力为0.130 34 MPa(15 psia)的等效阻力系数归一化处理，得到归一化等效阻力系数：

主要是由于此压力与安全壳内的压力接近，ADS4管路的支配压降为摩擦压降，加速压降可忽略不计。因此，计算的ADS4管路压降与NOTRUMP-AP600中不考虑缺失动量通量项的结果相差不大。图4示出ADS4管路在不同热段压力和含气率下的流量。图5示出不同压力和含气率下ADS4管路的归一化等效阻力系数。从图5可见，归一化的等效阻力系数随热段压力发生变化，在应用到AP600电站时，所取的归一化阻力系数对应如下压力：

pHL=patm+ρlgHIRWST

(36)

式中：pHL为热段压力；patm为安全壳内压力；HIRWST为IRWST与热段之间的高度差。

含气率由下至上依次为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0

对于AP600，IRWST高于热段的名义水位，为9.75 m，对应的热段压力约为0.193 0～0.206 8 MPa，对照图5中的归一化阻力系数为1.6，故对于AP600电站阻力系数增加60%。将阻力系数增加用于NOTRUMP-AP600程序后，计算的稳压器坍塌水位(单位为英尺，ft)和IRWST注射流量(单位为磅/秒，lbm/s)与实验值的对比如图6所示，可见符合较好。

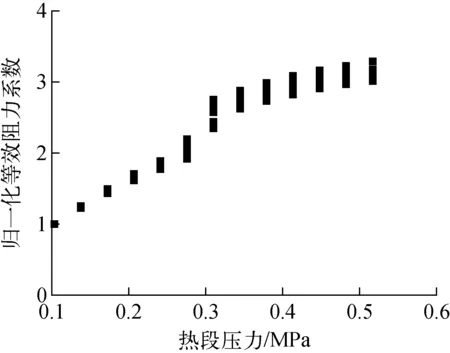
含气率由下至上依次为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0

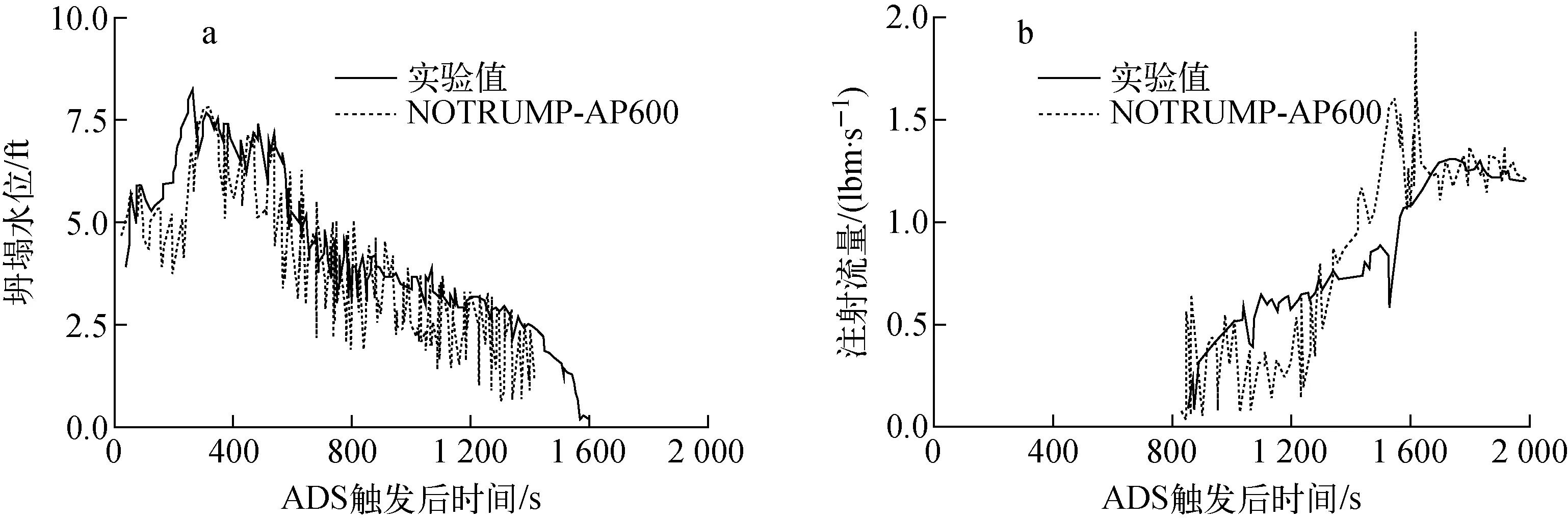
图6 阻力系数修正后稳压器坍塌水位(a)和IRWST注射流量(b)

4 结论

NOTRUMP-AP600程序中动量守恒方程的动量通量项的缺失将会引起ADS1～3管路和ADS4管路两相压降预测出现误差。对于ADS1～3管路，相对误差不超过10%，认为此误差范围是可接受的。对于ADS4管路，相对误差较大，必须对动量守恒方程加以修正。对于AP600电站，ADS4管路阻力系数应增加60%，修正后预测结果和实验数据符合良好。

参考文献：

[1] FITTANTE R L, GAGNON A F. NOTRUMP final validation report for AP600, WCAP-14808[R]. USA: Westinghouse Electric Corporation, 1998.

[2] 徐济鋆. 沸腾传热和气液两相流[M]. 北京：原子能出版社，2001.