一种基于外存的海量地表离散点的交互编辑算法

鲁 强，席鹏翰*，朱俊诚，王智广，刘 鑫

(1 中国石油大学(北京)地球物理与信息工程学院，北京 102249；2 中国石油化工股份有限公司石油勘探开发研究院，北京 100086

随着航拍、激光扫描等三维遥测技术的日益发展，获取的地形数据体规模也随之增大，基于内存的绘制显示技术已经不能满足要求，因此出现了大量的基于外存的绘制算法，有效解决了内存大小对海量地形数据的限制.基于外存的算法是对这些数据进行有效地组织，建立索引机制以支持后续的数据分析、实时交互操作等.

为了获取更多的地表信息，在地形表面上按照一定规律再以离散点的形式增加显示一层数据，点的规模大，且分布范围任意，可布及整个地表，也可只占地表中的一部分.此时，需要对地形数据和点数据同时进行绘制显示，并且还要能对这些点进行交互操作以满足工业要求.本文通过对增加的离散点数据进行分析，定义了合适的索引数据结构，实现了与地形数据统一调度的算法，并在此基础上实现交互操作，满足了实际应用的要求.

1 海量地表离散点的处理

海量点数据处理的关键就是找出点之间的关系，通过一定的数据组织方式建立相应的空间索引结构，同时存储相关特征信息，有助于数据的查询.常见空间索引一般为自顶向下逐级划分的结构，比较有代表性的包括KD树、R树系列、四叉树和八叉树等，而在这些结构中，四叉树在二维平面点数据中应用较为广泛，KD树和八叉树常用于三维点数据组织中.

四叉树是由Raphael Finkel与J.L.Bentley在1974年提出来的一种树状数据结构，其结构比较简单，当空间数据对象分布比较均匀时，具有较高的空间数据插入和查询效率.KD树是一种面向k维空间点的二叉树结构，是一种较为有效的k维空间点数据组织结构，在涉及高维空间查找领域具有自身独特优势.八叉树是由Hunter在1978年首次提出的一种数据结构，是四叉树在三维空间上的扩展.Surfels和QSplat[1，2]系统则是在八叉树的基础上提出了基于点的多分辨率表示，Surfels根据固定间隔的采样点构成八叉树，而QSplat是基于包围球构成八叉树，但是这两个系统都不能有效的支持动态修改.Wand等人[3]介绍了一种实现海量点交互的算法，在八叉树非叶子节点中保存一个量化后的网格，网格中用一个三维坐标点来表示当前节点所包含的所有三维坐标点.为了便于交互，给网格中的坐标点一个权值，当有交互操作时更新权值.该系统使用了将近三倍于实际坐标点数据大小的磁盘空间，数据多次重复，造成了很大的浪费.Claus等人通过使用一种基于嵌套八叉树[4，5]结构的算法，减少了内存消耗并实现了海量点的快速渲染绘制，实现了点的添加、删除等交互操作.但上述两种算法中的数据结构都不足以支持更为复杂的交互操作.根据实验离散点的特征，即所有点都平铺在地形表面上，每个点的z轴坐标值在绘制时通过获取地形数据中与此点x、y轴坐标值一致或者邻近的点，再进行插值计算得出，故在未使用z轴坐标值之前，可将这样的三维点集视为二维坐标点集，通过四叉树对之进行划分，降低了数据结构的复杂性.点按作用类型又可分为两类，且这两类点分别组成多根线.以线为单位，对线上的点进行操作可作为一维空间的操作，而一维空间的数据检索可通过区间树与二分查找算法来实现.

综上，借鉴嵌套数据结构的思想，对四叉树和区间树做相应的改进，实现一个复合嵌套结构对海量地表离散点进行组织，形成两级索引，有效地解决了上述问题，同时也更好地实现了实时绘制和交互操作.

2 嵌套四叉树

嵌套四叉树的数据结构便于存储、检索以及实时交互操作的实现.先将整个离散点集以线为单位建立索引，每根线划分成多个块进行读写，再当构建四叉树结构时，根据节点区域范围保存相关线的索引数据，不再保存当前节点范围内所有点的坐标值.下面将逐一介绍每一部分的设计与实现.

2.1 改进的区间树索引

通过对实验三维点数据分析，这些点组成大量的三维空间线.在整个三维点集中查询一个点可分解为查询某一根线，再从这根线查询这个点.故对此三维点集合建立合适的线索引，既能快速地检索到线，又能通过线的索引数据加快点的查询.利用二分查找算法在一维空间中查找点的优势，对区间树作一定的修改，实现所要的线索引结构，该结构图如图1所示.

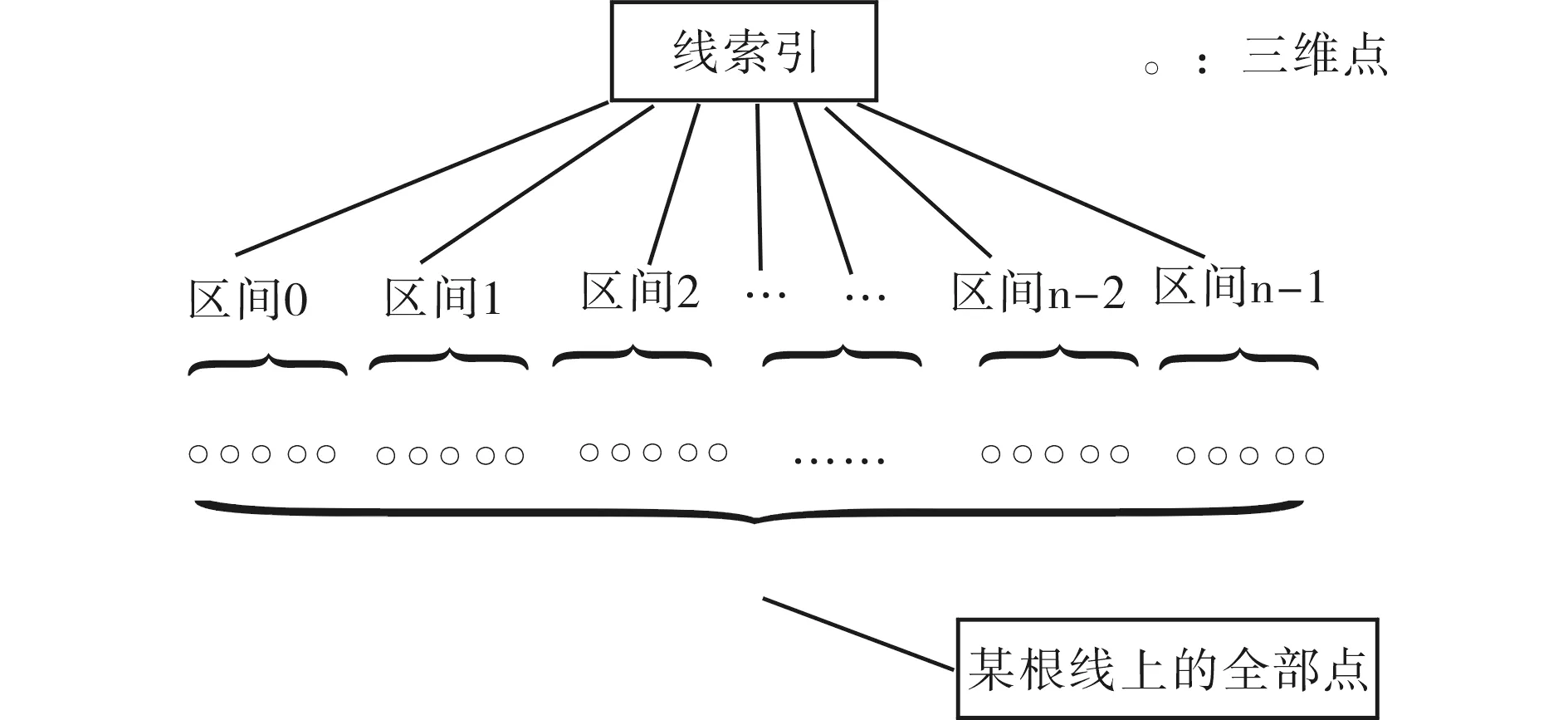
图1 线索引示意图Fig.1 Schematic diagram of line index

图1中表示的三维点在空间的分布形态不规则，可为直线状、曲线状或环状等，所以单纯的以x轴坐标值或y轴坐标值作为查询基准不能实现点的精确检索，若同时用x、y坐标值进行查询则会造成空间的浪费.由于每根线上点的编号唯一，且按递增的规则从第0个点开始一直计数至最后一个点，故可将点的编号作为检索基准，进行区间划分，实现索引结构.区间划分的过程与建立区间树类似，通常在建立区间树结点时，对所有区间按照左端点(或者右端点)进行排序，然后逐层确定单元边数目的中位数，将该位置的值作为各级结点的关键字[6].为了更好的适应点数据特征，记录每个区间中第一个点的编号及该区间中点的个数.在进行三维点查询时，需要先确定这个点所在的线.由于同一种类型各线的编号都不一样，所以可通过两个map结构分别将对这两类线的索引进行组织，map的key为线的编号，value为这根线的索引记录PointLineIndex.在建立线的索引数据时，通过两个不同的文件流同时将点的坐标值和索引数据写入两个不同的文件中，三维点的坐标数值按照x、y、z轴的顺序依次写入，且此时z值为0，索引数据按照map结构一一对应写入文件.同时在内存中也保存了这个map结构，使内外存结构相一致，以便在数据量超大时，有效地实现内外存数据的读写，用来建立瓦片四叉树.

图2 线索引数据结构Fig.2 Data structure of line index

线索引的数据结构定义如图2所示，其中isHLine用于区分线的类型，m_lineID为线的编号，m_lineOffset为这根线在数值文件中开始记录的偏移位置，m_lineBlockNum是这根线分成的区间个数，m_startPoint记录了这根线上起始点的x、y轴坐标值，m_endPoint记录了这根线上终止点的x、y轴坐标值，m_ptNumBlockVect记录了每个区间中点的个数，m_blockStartPosVect记录了每个区间中第一个点的编号.在这个数据结构中，最为关键的是m_ptNumBlockVect和m_blockStartPosVect.因为若只记录这根线的编号，以及起始点坐标和终止点坐标，虽然节省了一定的内存空间，但是在查询某一点时，仍要将整根线的数据全部读出做比较，会造成时间和内存空间的浪费；若将线上点编号全部记录在索引中，虽然能够很快的定位到某一个点，但是当整个点集的规模很大时，必定会占用很大一部分内存.而合理的划分块大小，记录每一个块的起始点编号，通过比较待查询点编号与各个块的起始点编号，能够快速定位待查询的点所在区间块号.这样既节省了一定的内存空间，又能提高查询的效率.

当线中的点全部写入文件后，这根线的索引数据也全部完成并写入相应索引文件中，同时在内存中保存着线索引数据结构.这样给出线的编号、类型及线上一个点的编号，实现在点集中检索点的算法如下：

Algorithm: Find_The_Point_In_Line()

Input:LineID = lid, bool isHLine = true, PointID = pid;

1) PointLineIndex plidx = GetPLIdxByLineID(true, lid);

2) int m = binarySearch(pid, plidx.m_blockStartPosVect);

3) std::vector*Ps = readBlocks(m, m, plidx);

4) Point p = FindSP(Ps, pid);

Output: p，p为待查询点.

由此算法可知，第一步根据线的类型和编号，通过键值映射直接获取索引，第二步由索引中每个区间块首点编号与待查点的编号，使用二分查找算法来确定区间块号，第三步是根据确定的区间块号读出个区间块中的数据，最后再通过二分查找算法在这个区间块中找出该点.由于每根线上点的个数都不一定相同，在生成线索引时会使线索引记录长度不一致.为了更好的解析线索引记录，对每根线索引再建立了一个索引，记录此线索引的线编号，索引记录在索引文件中的起始偏移及索引长度.

2.2 基于线索引的四叉树

在建立四叉树时，根据离散点集的x、y轴方向上的平面范围及欲建立的四叉树层数，自顶向下进行规则划分.以一个四叉树节点为例，节点的数据结构中包含多个属性值.可以通过当前节点的编号先计算出占据的二维平面范围.为了保证每个节点中数据的准确性，需要通过遍历每一根线上的点，确定出当前节点范围包含了哪些点数据.遍历时，记录所包含的线编号，以及每根线在这个节点平面范围内经过的第一个点和最后一个点，根据这两个点的编号通过线索引确定当前节点范围包含的区间块号，图3为四叉树索引与线索引的关系图.这样建立起的四叉树索引中，每个节点都保存了所包含线的区间块编号和点的编号.四叉树节点的数据结构定义如图4所示，其中m_tID为四叉树节点的编号，extents[4]记录当前节点的x、y轴平面的最大、最小值，ptsNum为此节点范围内包含的点的总个数，sample是显示当前节点时要用的采样间隔，hlNum为此节点包含的第一类线的个数，hlidx为此节点中包含第一类线的每个线索引记录，每根线的索引记录包含了这根线的编号，这根线在此节点范围内的起始点编号、终止点编号以及这两个点所在的区间块号，vlNum与vlidx表示为第二类线的个数及索引.

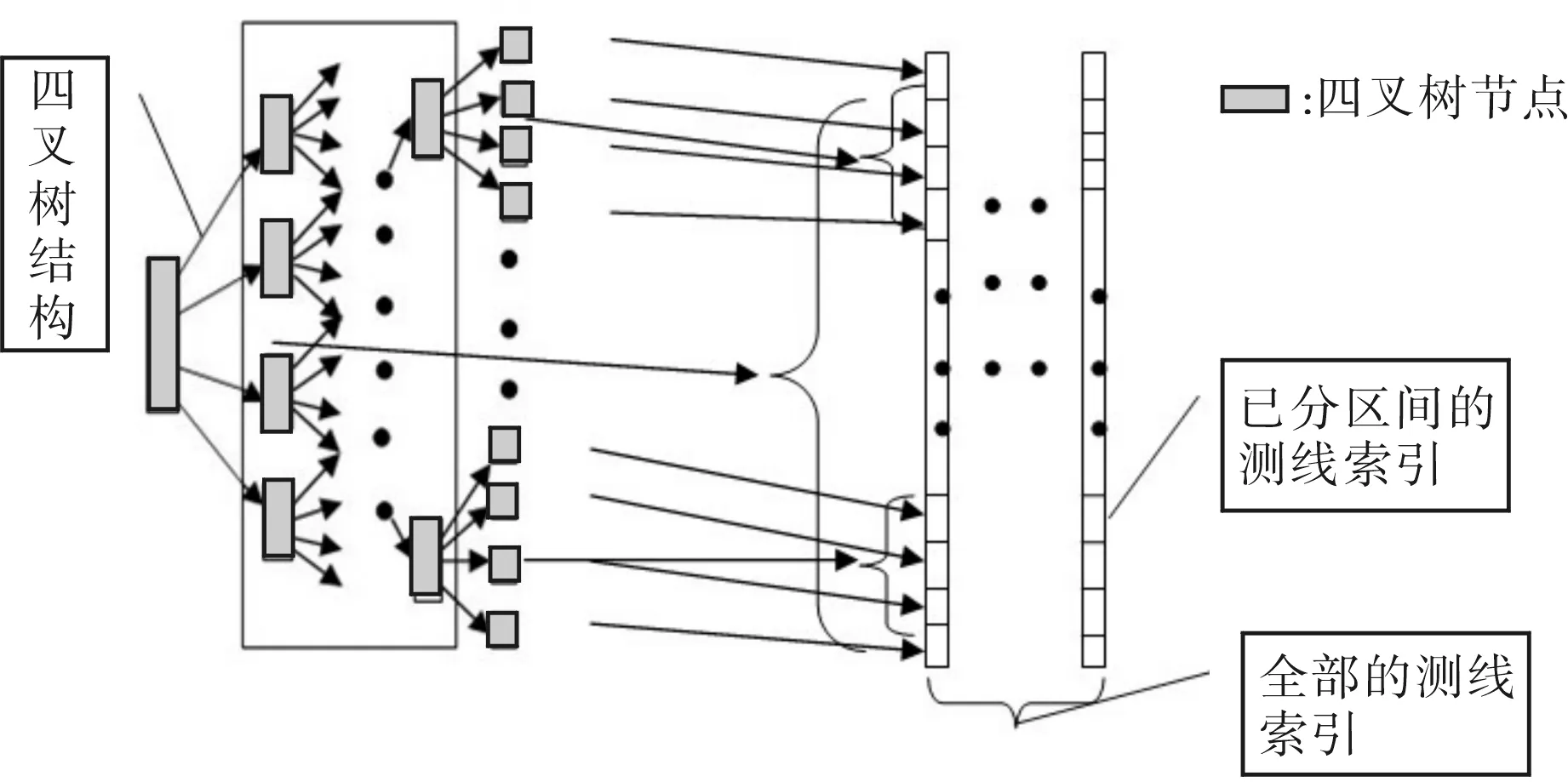
图3 四叉树与线索引关系图Fig.3 Schematic of quad-tree and line index

图4 四叉树节点数据结构Fig.4 Data structure of quad-tree node

当整个四叉树建好之后，查询整个点集中的一个点可缩小至查询某个节点范围内的一个点.这样给出一个节点的编号，以及选中的线编号及类型和待查询点编号，查询算法如下：

Algorithm: Find_The_Point_In_Tile()

Input:Tile_ID = tid, LineID = lid, bool isHLine = true,PointID = pid;

1) TileIndex tidx = GetTileIdxByID(tid);

2) if(isHLine == true)

int m = GetBlockNum(tidx.hlidx[lid], pid)

3) std::vector* Ps = readBlocks(m, m, plidx);

4) Point p = FindSP(Ps, pid);

Output: p，p为待查询点.

由这个查询算法可知，通过节点编号获取该节点的索引数据，再由线的编号在此节点索引中找出相应的线索引数据.因为节点中的线索引已经缩小了范围，越是底层节点，该范围就越小，从而减小了查询的难度.最后在确定的区间范围里，通过二分查找算法获取该查询点数值.

由于常用地形数据集的大小远远超出了内存大小，通过四叉树对之进行组织处理，使视域范围内的地形块根据视点移动产生的视距变化而不断更新.而地表上的离散点经过四叉树的划分后，每个节点可根据自身的extents范围值求出相应的最近、最远可视距离，此可视距离与地形数据集的可视距离相匹配，实现两者的统一调度.为了更好地实现交互操作，在建立四叉树索引时记录了每根线所经过的全部四叉树节点，将之作为一个单独的索引结构写入文件，同时在内存中构造与之相对应的数据结构.当出现删除一根线的交互操作时，可直接通过待删除线的编号直接查找出全部与之相关的四叉树节点，再依次更新这些节点中的线索引，若没有这样的数据结构，则需要一一遍历每个四叉树节点，查询节点中是否包含这根线，浪费大量的内存空间和时间.

3 交互操作

满足显示要求后，可对离散点数据进行交互操作.交互操作按操作的对象可分为点、线、区域这三类，按操作的类别可分为选中、删除、添加、移动这四种.下面则按操作的对象依次分析各操作的流程.

3.1 点的交互操作

3.1.1 删除点

由于地形数据的范围很大，会出现一些无效区域，如河流、峡谷等，分布在这些区域中的点则为无效点.将这些无效点删除时，将点的x、y、z轴的坐标值都更改为-99999，当再次读取到这些点时，可根据坐标值判断而过滤掉这些点，使之不再绘制显示出来.这个方法不需要更改线索引和四叉树节点索引，降低了操作的复杂度，节省了时间和内存空间.图5(a)为单点删除的效果图，黄色矩形框中原本为五个蓝色点，从左往右删除了第二个蓝色点.

3.1.2 插入点

当某一地形区域中的点分布稀疏，而又要准确地获取这一地区的详细信息，可在已有的点之间再插入多个点，根据地形数据中的z值实时计算出这些点的高程值，使之紧贴地表.可先选中当前区域中的一根线，在此线上某两点之间插入一个点.为了保证交互的实时性，在插入点时直接计算出新插入点的坐标值及编号进行实时绘制显示.给出插入的点，待插入线的类型及编号，插入单点的算法实现如下：

Algorithm: Insert_Single_Point()

Input: Point sp, LineID = lid, isHLine = true;

1) PointLineIndex plidx = GetPLIdxByLineID(true, lid);

2) int m = binarySearch(sp.pid, plidx.m_blockStartPosVect);

updateLineidx(lineid);

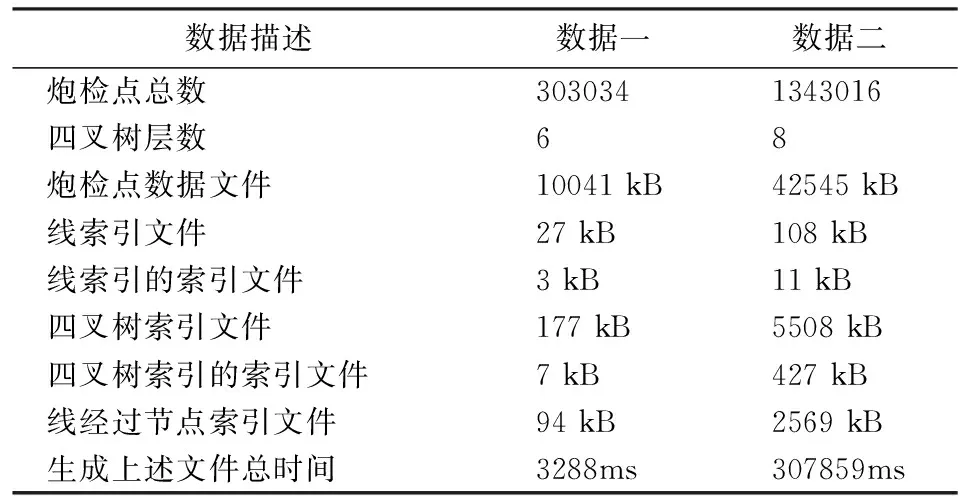
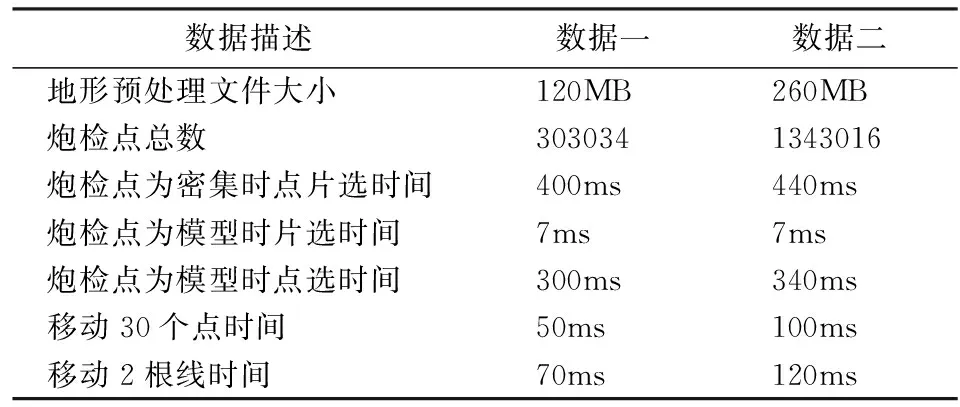
3) std::vector tiles = getTiles(lineid);

for(inti=0; i

if(tiles(i).extents.isContain(sp.xy()))

updateTileIndex(tiles(i));

4) std::vector* Ps = readBlocks(m, m, plidx);

Ps.insert(sp);

5) writeBlocks(lineid, m, m, Ps);

由插入点算法可知，第1步找出该线的索引数据；第2步确定待插入点所在区间块号并更新此区间块中点的个数；第3步通过线经过四叉树节点的索引找出所在线对应的全部节点，判断每个节点的extents范围是否包含新插入的点，若包含这个点则需要更新节点的ptsNum值，若不包含则无需更新；第4步则是读出此线该区间里的全部数据，并将新加点按照编号插入其中；第5步则将更新后的区间点数据重新写回数据文件中.图5(b)为插入单点的效果图，黄色矩形框中有一白色点为选中点，在其右下方为新插入的红色点.

在首次写入三维点集数据时，每一个数据块分成相等的两部分，一部分为区间块中的点坐标值，另一部分为空白区域，所以一个区间中可最多插入与区间点数同样多的点，且readBlocks()与writeBlocks()函数都是以数据块为最小单元实现读写.由于索引与数据的更新实现分离，有利于场景实时绘制.当有多次相同交互操作时，通过后台线程先实时更新索引，满足一定交互次数后，再将更新后的数据写回文件.

3.1.3 移动点

当地形上出现一些障碍物，如高楼、山峰等时，可将原先在此区域中的点移至其它区域.给出待移动点，此点所在线的编号和类型及移动的距离，移动单点的算法实现如下：

Algorithm: Move_Single_Point()

Input: Point sp, int offset, LineID = lineid, isHLine = true;

1) Point nsp;

nsp += offset;

2) tileID = CaculateTID(sp)

3) for(int l=tileID.level; l>=0; l--)

ptileID = getParent(l);

if(Tile[ptileID].extents.isContain(nsp)==false)

updateTileIndex(Tile[ptileID]);

4) PointLineIndex plidx = GetPLIdxByLineID(true, lid);

int m = binarySearch(sp.pid, Lidx.m_blockStartPosVect);

5) std::vector* Ps = readBlocks(m, m, plidx);

if(Ps[j] = sp.ID)

Ps[j] = nsp;

6) wrtieBlocks(lineid, m, m, Ps);

由移动点算法可知，第1步创建一个点的新实例对象，将移动后的新坐标值赋值给新的点对象；第2步根据原坐标值确定其属于四叉树最底层的哪个节点；第3步由最底层节点开始，向上依次找出四叉树每一层中最底层节点的父节点，并判断父节点是否包含移动后的点，如果包含则无需修改该节点的索引，如果不包含则需要更新该节点的索引，主要为更新该节点的extents范围值；第4～6步则是将移动后的点坐标值重新写入文件.整个过程只更新相应四叉树节点索引，降低了难度.当有多次移动点的操作时，也可先更新内存中的四叉树节点索引，最后再将更改后的坐标数值全部写入数据文件中.图5(c)为移动单点的效果图，黄色矩形框中本为5个在一条直线上的蓝色点，从左往右将第二个蓝色点移动至左上方.

图5 单点的交互操作效果图Fig.5 Interactive operate of single point

3.2 线的交互操作

3.2.1 删除线

当无效区域范围很大时，可能整根线上的点都在无效区域中，此时可将这根线删除.删除线可以看作是删除多个点，给出待删除线的编号及类型，删除单根线的算法实现如下：

Algorithm: Delete_Single_Line()

Input: LineID = lineid, isHLine = true;

1) PointLineIndex plidx = GetPLIdxByLineID(true, lid);

2) std::vector* Ps = readBlocks(0, plidx.blockNum-1, plidx);

for(int j=0; j

Ps[j]= -99999;

writeBlocks(lineid,0, Lidx.blockNum-1,Ps);

3) updateLineIndex(Lidx);

4) std::vector tids = getIDsByLine(lineid);

for(int i=0; i

updateTileIndex(tids[i]);

由删除线的算法可知，第1步根据线的编号检索出对应的线索引；第2步则根据线索引读出此线上的全部点，将每个点的x、y、z轴的坐标值更新为-99999并再次写回数据文件中；第3步将内存中的这根线索引记录清除，并同步更新至外存线索引文件，重写其中内容；第4步则是根据线经过四叉树节点索引，获取所有包含此线的节点并更新，将其中对应的线索引记录清除.整个过程将数据的更新与线索引、四叉树索引的更新分开，简洁明了，如果按照传统四叉树的方法，则需要更改最底层中包含此线的每个节点里相关点数据，过程相对复杂.图6(a)中白色线为选中线，图6(b)中则将选中的线删除.

3.2.2 移动线

若线的初始位置不合适时，可选中线并将整根线移动至合适的位置.给出移动线的编号及类型，移动的距离，移动单根线的算法实现如下：

Algorithm: Move_Single_Line()

Input: LineID = lineid, isHLine = true, int offset;

1) PointLineIndex plidx = GetPLIdxByLineID(true, lid);

updateLineIndex(Lidx);

2) std::vector tids = getIDsByLine(lineid);

for(int i=0; i

updateTileIndex(tids[i]);

3) std::vector* Ps = readBlocks(0, Lidx.blockNum-1, Lidx);

for(int j=0; j

Ps[j] += offset;

4) writeBlocks(lineid,0, Lidx.blockNum-1, Ps);

由算法流程可知，第1步先获取线索引并更新线索引记录中的起始点坐标、终止点坐标；第2步是根据线编号找出所有包含此线的四叉树节点，依次更新每个节点中的数据，因为线中的点移动后，可能会超出原节点extents范围，故根据节点中对应的线索引获取此节点范围内的点并更改坐标值，判断是否需要更新索引数值；第3步则根据线索引按块将线上点数据读出，修改x、y轴坐标值，z轴上的值则在绘制显示时实时计算；第4步为写回更新后的点数据.图6(c)中则将选中的线向右移动了一定距离.

图6 线的交互操作效果图Fig.6 Interactive operate of single line

3.3 区域操作

3.3.1 区域删除

选中一片区域内的点，删除区域点操作分解为多次删除单点.将这些点的坐标数值更改为-99999，作为无效点，无需改变任何索引数据.图7(a)为选中区域点图，白色为选中点；图7(b)为删除区域点图.

3.3.2 区域移动

选中一片区域内的点，拖拽移动至任意位置，实时更新这些点的坐标数据.采取的算法策略是将这片区域点分解成每一个点的移动操作，更新内存索引数据后将新的坐标数据写回文件.图7(c)为移动区域点图.

图7 区域点交互操作图Fig.7 Interactive operate of area points

4 结果分析

对本文提出的算法加以实现，应用于地震勘探中三维地形与三维观测系统，实现了快速浏览显示和实时交互.测试平台为DELL PrecisionT3500，CPU Intel(R) Xeon(R)W3503，内存6.00G，硬盘ST31000524AS 1TB 7200r/s，显卡NVIDIA Quadro600，Windows7 64位系统.测试中生成两组实验数据，如表1所示.

表1 验数据属性表Tab.1 The attribute of experimental data

由表1中两组数据可见，第一组中生成了约30万个点，建立6层的四叉树；第二组中生成了约134万个点，建立8层四叉树.每一组数据都生成6个二进制文件，其中炮检点数据文件仅保存点的三维坐标信息，第二组此文件大小约为第一组的4倍，这与点数之间的倍数一致；线索引文件记录了线的索引信息，第二组的此文件大小也是第一组此文件大小的4倍；线索引的索引文件记录了每一根线的编号、在线索引文件中的起始位置和偏移长度，故每根线在此文件中的记录长度相同，通过对线索引文件再做一个索引后，再次读取线索引文件时就能更快的解析其中的内容；四叉树索引文件是记录了每一个节点中的信息，第二组中的此文件比第一组的大很多，因为当四叉树层数增加时，节点个数是呈几何级数增长；四叉树索引的索引文件是只记录了每一个节点的编号、在四叉树索引文件中的起始位置和偏移长度，故每个节点在此文件中的记录长度一致，其作用与线索引的索引文件一样，为了更快的解析四叉树索引文件；线经过节点索引为四叉树索引的一个逆向索引，因为四叉树节点索引结构中保存了该节点包含的线记录，此索引则记录每根线所经过四叉树节点，更有利于交互操作的实现.第一组数据生成这6个文件用时3288ms，第二组数据用时307859ms，时间增长幅度较大.因为文中为了使每个节点都能获取准确的数据信息，每个节点索引都遍历一次全局点数据的方法，故四叉树层数越高，节点数越多，从而花费的时间也就越长.再分别对上面两组数据进行相关的交互操作，并记录交互操作所用的时间，数据如表2所示.

表2 交互操作用时表Tab.2 Time of the interactive operate

由表2中数据可知，当点的规模大幅度增加时，不同类型的交互操作所用时间并未出现明显增加，表明了文中提出的数据结构在交互操作中保持了良好的稳定性，不会因数据量的增长而降低交互操作的实时性，可见嵌套四叉树的三维观测数据组织策略有效提高了炮检点渲染的实时性，而且为整个系统节约了大量的资源用于处理其它事务.

5 结束语

本文对基于外存海量地表离散点的交互操作算法进行了深入的论述，在区间树、四叉树索引的基础上提出了一种新的数据结构，即二者相结合的嵌套四叉树.该数据结构有效地解决了外存数据的快速存取、实时绘制以及实时修改难以同时实现的问题，尤其在进行交互操作时，通过先对内存索引和数据进行实时更新，再根据一定的策略更新外存数据，在不影响用户体验的情况下，大大简化了数据的计算流程.最后将该算法应用于地震三维观测系统平台，对算法进行了有效地检验，证明了算法的可行性.

由于在构建嵌套四叉树的过程时，为了精确计算每个节点的范围及其包含的线和点，使得当四叉树的高度增加时，建树所消耗的时间会大幅度增长.未来，将进一步研究在保证数据准确性的情况下，提高构建四叉树的效率；同时还可以对索引数据结构做更多的优化，有利于增加其他类型的交互操作，实现操作的多样性，以满足更多的用户要求.

参 考 文 献

[1] Pfister H, Zwicker M,Baar J V, et al. Surfels:surface elements as rendering primitives[C]//ACM SIGGRAPH. Proc SIGGRAPH′00(2000).Louisiana:ACM SIGGRAPH,2000:335-342.

[2] Rusinkiewicz S, Levoy M. Qsplat: a multi-resolution point rendering system for large meshes[C]//ACM SIGGRAPH. Proc SIGGRAPH′00(2000).Louisiana:ACM SIGGRAPH,2000:343-352.

[3] Wand M, Berner A,Bokeloh M, et al. Interactive editing of large point clouds[C]//Eurographics.Symposium on Point-Based Graphics. Prague: Eurographics Association,2007:37-45.

[4] Scheiblauer C, Wimmer M. Out-of-core selection and editing of huge point clouds[J].Computers & Graphics,2011,35:342-351.

[5] Wimmer M, Scheiblauer C. Instant points:fast readering of unprocessed point clauds[C]//Eurographics.Proceeding SPBG′06 Proceedings of 3rdEurographics.Massachusetts:Eurographics Association,2006:129-136.

[6] Kreveld M V. Efficient methods for isoline extraction from a TIN[J]. Interational Joumal of GIS,1996, 10: 523-540.