基于DCT-CS和ATC的联合信源信道编码

汪汉新，汪亚芬

(中南民族大学 电子信息工程学院，武汉 430074)

联合信源信道编码(JSCC)是将信源编码压缩信息的特性与信道编码纠错的特性联合起来考虑，使得整个通信系统的传输性能达到最优化的编码方法.压缩感知(CS)是一种全新的信号处理理论，具有优秀的压缩性能，它突破了传统的香农定理和奈奎斯特采样频率的限制，使得采样和压缩能同时进行[1-2].然而压缩后的信息由于噪声的干扰，使得恢复的信号质量大大的降低，特别是在低信噪比情况下显得更为突出，因此压缩后的信息通常需要采用纠错编码来提高恢复信号的质量.虽然Turbo码是一种抗干扰性能极强的纠错码，但是它在低信噪比下的性能与高信噪比下的错误平台存在不平衡的问题，而非对称Turbo码(ATC)可以很好地解决这一问题，实现在整个信噪比范围内具有好的纠错性能.目前，基于图像的联合信源信道编码的研究取得了相应的研究成果[3-5]，但是将压缩感知理论应用于联合信源信道编码的图像压缩传输的研究还比较少.本文提出了一种基于离散余弦变换(DCT)的压缩感知编码与非对称Turbo码的联合信源信道编码方法，可以根据不同的信道环境来选择不同的图像分块大小和压缩感知的各项参数以及非对称Turbo码的编码策略，实现图像的传输速率和重构质量的优化平衡.

1 基于DCT的压缩感知编码(DCT-CS)

DCT变换是酉变换的一种，其信号熵和能量在变换前后不变[6]，且在时域中的变换核可以分为正、逆DCT，定义如下：

(1)

(2)

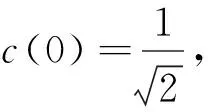
压缩感知通过一个与变换基不相关的观测矩阵将信号投影到一个低维的空间作为测量数，再通过测量数来求解一个最优化问题就能够精确的恢复出原始信号.对于长度为N的信号x，若x是非稀疏但可压缩，在Ψ基下能稀疏表示为：

x=Ψs,

(3)

其中s是稀疏的，则存在一个与稀疏基Ψ不相关的测量矩阵Φ：

y=Φs,

(4)

得到测量向量y，由于式(4)是欠定的，有无穷多个解，但s是稀疏的，因此可以通过求解式(5)的最小范数问题从测量数y中精确重构s：

(5)

其中Θ=ΨΦ，再通过式(3)恢复原始信号x.压缩感知的重构算法由式(5)来求解，即求解一个最小l0范数，然而它是一个NP-hard问题，故将其转化为范数问题来求解.当Θ=ΨΦ满足约束等距性RIP时，最小范数问题可以转化为最小范数问题，即式(3)变为:

(6)

如果压缩感知的信号是稀疏的，则可以找到一个观测矩阵对其进行测量，再以优化的重构算法精确的恢复原始信号，大大的减小采样数据量和采样时间，节约存储空间.传统的二维DCT图像压缩编码中，提取前若干较大的低频系数作为特征分量，后面高频系数则用零代替，此时的系数绝大多数为零，即可以认为此信号是稀疏的，因此可以将DCT变换作为压缩感知的变换基.

本文的压缩感知重构算法采用凸松弛法中的NESTA重构算法[7-8]，将非凸问题转化为凸问题来求解得到信号的逼近，是一种快速精确的一阶稀疏恢复算法，观测次数少且精度高，由Nesterov算法扩展而来[9-10]，算法结合光滑逼近思想和梯度法技术，解决压缩感知恢复算法中的最小l1范数的最优化问题.在压缩感知中最主要的问题是求解式(6)，在稀疏基Ψ与感知基Φ不相干时，式(6)在高概率下存在公共解.而事实上测量向量y通常带有噪声，且s可能是近似稀疏，不能很好的恢复原始信号，可以将式(4)转化为求解最小二乘问题，如式(7)：

(7)

其中参数λ与式(5)中约束条件的参数有关，用来在极小化过程中平衡式(7)的前后两项.而由于在求解最小l1范数时涉及的函数往往是一个强凸函数，因此利用Nesterov算法来进行光滑逼近求解函数的最小值.

2 非对称Turbo码(ATC)的设计

非对称Turbo码是由两个不同结构的递归系统卷积码RSC、交织器、删余器和复接器组成.它与对称Turbo码的不同之处在于两个分量码是具有不同约束长度或者不同类型生成多项式的RSC码.编码约束度是决定Turbo码译码复杂性的主要因素之一.研究表明采用编码约束度较小的分量码在复杂性较小时可以达到较好的性能，但小编码约束度分量码的自由距离比较小，会出现较高的错误平层，因此为了实现码字性能和复杂性的折中，可以选择减小其中一个分量码的编码约束度[11].本原分量码可以降低高信噪比下Turbo码的错误平层，而非本原分量码则可以改善低信噪比下Turbo码的性能.当信噪比很小时，非本原分量码经过译码可以得到更有利于迭代译码的外部信息送到本原分量码对应的分量译码器，本原分量码在一定程度上提高Turbo码的自有距离，来提高高信噪比时的性能.因此与标准对称Turbo码相比，非对称Turbo码在整个信噪比范围内能具有更好的性能.非对称Turbo码有两类：I类是通过两个约束长度相同而生成多项式类型不同的RSC分量码并行级联组成；Ⅱ类是由约束长度不同而生成多项式类型相同或者不同的两个RSC分量码并行级联组成.表1给出了本文设计的两类非对称Turbo码的各种类型，其中K1和K2分别为两个RSC分量编码器的约束度，G1和G2为对应的多项式，P表示本原多项式，NP表示非本原多项式.

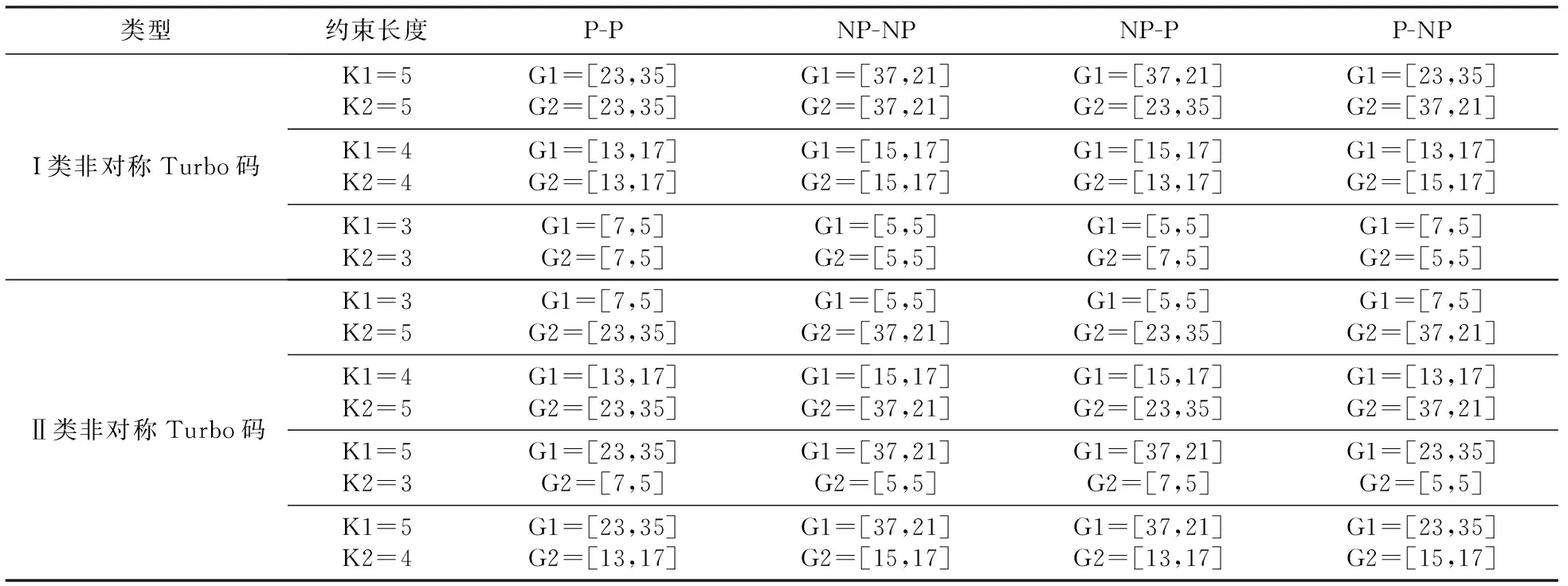
表1 两类非对称Turbo码

3 基于DCT-CS和ATC的联合信源信道编码

信源编码解决信息传输的有效性，信道编码解决信息传输的可靠性，而联合信源信道编码可以根据信道状况调整信源编码参数、信道编码方法或者根据信源特性调整信道编码方法，通过权衡信源编码和信道编码对整体失真的影响，合理分配资源，使系统整体性能达到最优.联合信源信道编码可以获得更好的性能，而系统的整体复杂性却得到一定程度的降低，更适合于资源受限、信道时变的复杂无线通信系统.DCT-CS具有非常好的压缩性能，ACT则具有很好的纠错性能，因此将两者结合实现联合信源信道编码，可以提高整个系统的传输性能.基于DCT-CS和ATC的联合信源信道编码的系统如图3.

图1 基于DCT-CS和ATC的联合信源信道编码Fig.1 JSCC based on DCT-CS and ATC

原始图像经过分块后进行DCT变换使其稀疏化，选取高斯矩阵作为观测矩阵进行测量，再将测量值进行非对称Turbo码编码，送入AWGN信道传输；根据信道状况的好坏来自适应的调整非对称Turbo码的编码策略以及不同的图像选择不同的分块大小和相应的压缩感知的测量数；接收端进行相应的译码，NESTA算法重构和IDCT变换，最后得到重构图像.通过信道估计，当信道环境较差的时候，系统自动的增大测量数，并采用纠错能力比较好的非对称Turbo码类型；当信道环境比较好的时候，减小测量数且使用纠错能力较差而编码复杂度较小的非对称Turbo码类型，甚至当信道环境非常好的时候，可以采用复杂度更小的RS码或分组码.

4 仿真结果与分析

仿真实验的信号源为灰度图像，压缩感知的测量矩阵为高斯矩阵，重构算法为NESTA，信道为AWGN，ATC的译码算法为Log-MAP.

表2是图像大小为256×256和64×64的Lena、Fingerprint以及Cameraman 图像分别使用不同的分块进行DCT-CS编码的仿真实验结果，其中P为分块的大小，PSNR为重建图像的峰值信噪比.从表2可以看出不同的图像在相同的分块大小时，重建图像质量有所不同.而相同的图像在不同的分块大小时，重建图像质量也有差异.因此，在联合信源信道编码时，可以根据原始输入图像的特性和信道状况的好坏，合适的选择图像分块的大小.

表2 采用不同分块时的重建图像质量PSNR/dBTab.2 PSNR/dB for different block images

表3是64×64的Lena图像在分块大小为8×8的情况下，使用不同的测量数进行DCT-CS编码的仿真实验结果，其中M为测量数.从表3可以看出测量数越大，重构质量越好，但复杂度也越高.因此在联合信源信道编码时，可以根据信道状况的好坏，合理的调整压缩感知的测量数大小.当信道状况较好时，可以采取小的测量数，实现在保证重建图像质量的同时，减小压缩感知的计算复杂度；而当信道状况变得较差时，则自动调整为较大的测量数.

表3 采用不同测量数M时的重建图像质量PSNR/dBTab.3 PSNR/dB for different measure data

表4为信道状况较差(信噪比Eb/N0=2.0dB)和信道状况较好(Eb/N0=4.0dB)时，基于DCT-CS和ACT的图像压缩传输的重建图像的峰值信噪比PSNR和运行时间T.其中，分块大小为8×8，测量数为32，K1和K2分别为两个RSC分量编码器的约束度.

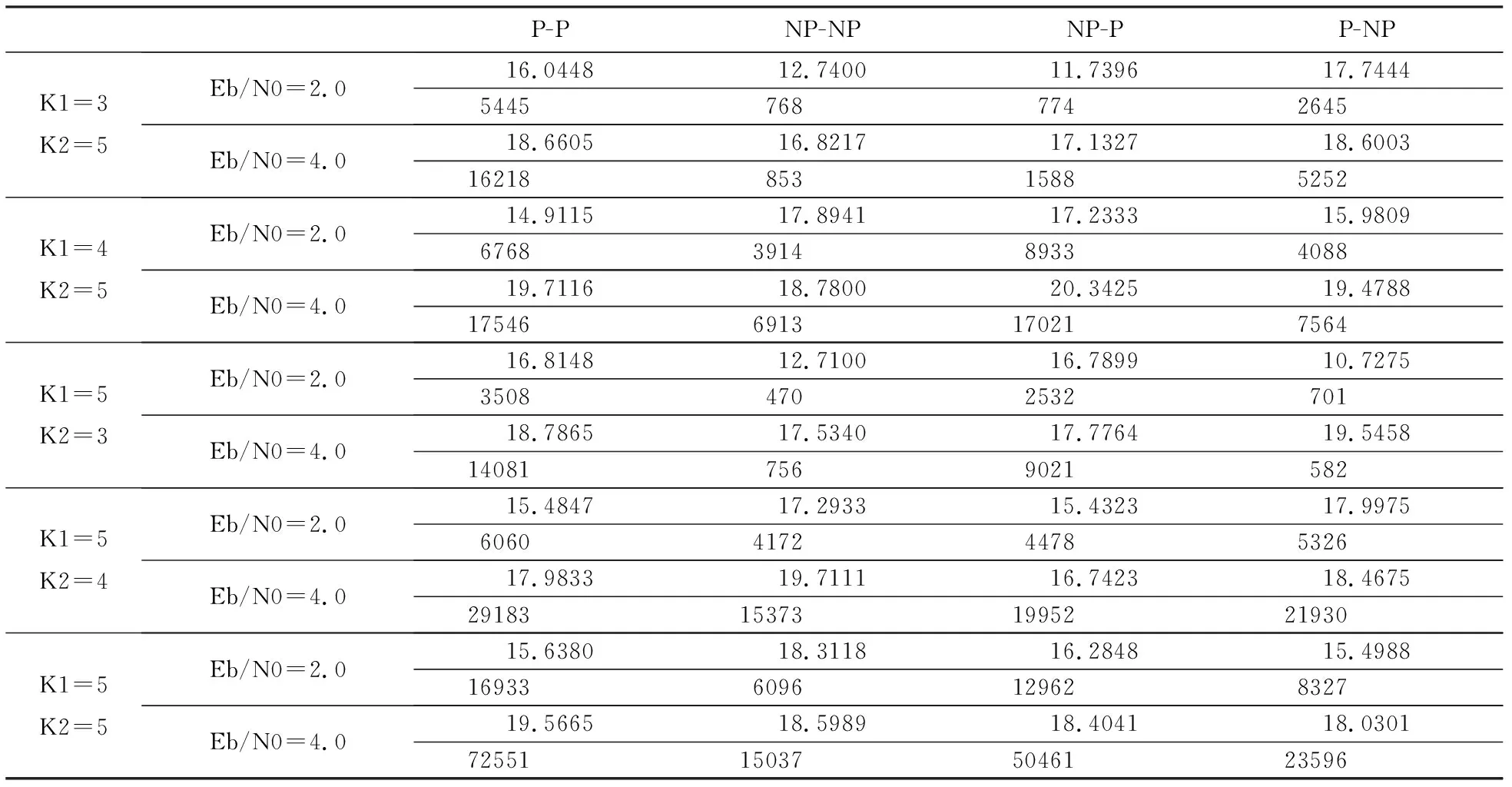
表4 不同信道环境下DCT-CS和ATC的JSCC的重建图像PSNR/dB和T/S

由表4可以看出，在不同的信噪比下，使用不同的非对称Turbo码，重建图像的质量以及传输速率都不同.因此，在联合信源信道编码时，可以根据信道状况的好坏，合适的选择非对称Turbo码的类型.当信噪比较低时，此时信道环境比较差，可以选择纠错性能较强的K1=K2=5，NP-NP类型Turbo码；而当信噪比较高时，即信道环境比较好的时候，可以选择复杂度较低的K1=3,K2=5,P-NP类型非对称Turbo码，从而实现重建质量和传输速率的优化平衡.

5 结束语

本文研究了以DCT变换作为稀疏基的压缩感知和非对称Turbo的联合信源信道编码，实验结果表明：DCT变换作为稀疏基的压缩感知具有良好的压缩性能，而非对称Turbo码具有极强的纠错能力，将两者进行联合信源信道编码，使得图像的重构效果和传输速率达到最佳的平衡，整个系统通过估计信道环境的好坏来自适应的调整压缩感知和非对称Turbo码的各项参数能够达到很好的传输效果.

参 考 文 献

[1] Donoho D L. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4):1289-1306.

[2] Candes E,Romberg J,Tao T.Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information [J]. IEEE Transactions on Information Theory, 2006, 52(2):489-509.

[3] 肖 崇, 吴成柯.无线信道的联合信源信道编码研究[D]. 西安:西安电子科技大学, 2004.

[4] 郭 锐, 刘济林. 基于JPEG2000和WIPC-LDPC的联合信源信道编码[J]. 中国图象图形学报，2008, 13(6):1048-1054.

[5] 陈俊宏, 张钦宇. 基于最优小波分组的联合信源信道编码图像传输系统[J]. 通信学报, 2012, 33(10):149-156.

[6] Huang Y M, Wu J L. A refined fast 2-D discrete cosine transform algorithm [J]. IEEE Transactions on Signal Processing, 1999, 47(3):904-907.

[7] Becker S, Bobin J, Candes E. NESTA: a fast and accurate first-order method for sparse recovery [J]. SIAM Journal Imaging Science, 2011, 4: 1-39.

[8] Maleki A,Donoho D L.Optimally tuned iterative reconstru-ction algorithms for compressed sensing [J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 330-341.

[9] 方 红, 杨海蓉. 贪婪算法与压缩感知理论[J].自动化学报, 2011, 37(12): 1413-1421.

[10] Nesterov Y.Smooth minimization of non-smooth functions [J]. Mathematical Programming, 2005, 10(3): 127-152.

[11] 刘东华.Turbo码设计与应用[M〗. 北京：电子工业出版社，2011.