一种改进的组签名平台配置远程证明机制

李宏宇，付东来

(1. 山西省财税专科学校网络中心，太原 03002 4；2. 中北大学电子与计算机科学技术学院，太原 03005 1)

一种改进的组签名平台配置远程证明机制

李宏宇1，付东来2

(1. 山西省财税专科学校网络中心，太原 03002 4；2. 中北大学电子与计算机科学技术学院，太原 03005 1)

针对远程证明效率低、隐私保护能力及可伸缩性差的问题，提出一种基于可动态调整的非平衡Merkle哈希树的平台配置远程证明机制。借鉴Merkle哈希树远程证明方案，考虑可信实体完整性度量值被请求的概率，综合利用组签名技术和动态Huffman

树构造算法的优势，不仅能大幅减少可信实体度量日志的存储空间，屏蔽具体的可信实体的哈希值，而且缩短认证路径长度。给出具体的软件分发算法、完整性度量和验证算法，并从验证效率、隐私保护和可伸缩性3个方面分析算法的优势。分析结果表明，该机制可提高远程证明算法的效率、隐私保护能力及可伸缩性。

可信计算；远程证明；组签名；Merkle Hash树；隐私保护；可伸缩性

1 概述

远程证明是通过远程机制验证平台是否可信的过程。根据证明内容的不同，可以将远程证明分为平台身份证明和平台配置证明2种证明机制。在平台配置证明方面，可信计算组织提出了基于二进制的远程证明方法。隐私泄露、可伸缩性差、通信和管理负载大等问题已经成为限制二进制远程证明方法进一步发展的主要瓶颈。因此，本文针对二进制平台配置证明方法存在的这些问题展开研究。

首先，在二进制平台配置证明方法中，终端平台为了获得远程平台的信任，需要提供所有的平台配置信息，包括操作系统和应用软件。显然，这可能使得终端平台的安全漏洞信息在无意中泄露出去，成为黑客的攻击目标。其次，大量的应用软件及系统软件使得度量参考列表及度量日志列表的可伸缩性成为该方法的主要瓶颈。据统计[1]，一次典型的Windows安装过程，需要从400万个已知的驱动集中装载2 000多个驱动程序，而且驱动程序的数量仍在以每天4 000个的速度快速增长。如果再加上大量的第三方应用软件，由度量参考列表和度量日志列表引发的可伸缩性问题将变得更加严重。最后由度量日志列表引发的通信和管理负载问题也是影响该方法进一步发展的障碍之一。

完整性度量架构IMA[2-3]是较早的一个完整的二进制平台配置证明方案的实现，它的主要缺陷是验证效率低且为静态度量。随后针对IMA的不足，研究人员分别提出基于软件分组的度量机制[4]和基于Merkle树的度量机制RAMT[5]。这2种度量机制都属于静态度量机制，无法保证可信实体在运行过程中的可信。为此，一些国内外学者分别提出了一些动态度量机制[6-8]。但上述2种机制不是相互排斥，而是相互补充、相互借鉴、相互促进的关系。

在以上研究成果的基础上，设计了一种可动态调整的非平衡的Merkle哈希树存储被度量的可信实体完整性哈希的方法。Merkle 哈希树最早用于解决公钥基础设施领域中的证书问题。由于通过Merkle哈希树的根节点的哈希能够保证全部叶子节点的完整性，因此只要根节点的哈希能够被可靠的保存，就能利用最小的可信空间存储大量的不可信空间的数据。

在可信计算领域，文献[5]提出了使用Merkle哈希树存储可信实体的完整性哈希的远程证明方案。然而，在有些应用场景中，即部分叶子节点被查询的频率高于其他叶子节点时，不平衡的Merkle哈希树的性能会优于平衡的Merkle哈希树，即叶子节点的平均查询路径要短。在密钥管理领域中，研究人员为了克服静态Huffman树的不足，提出了一种基于自适应的Huffman树组密钥更新方案[9]。在可信计算领域，文献[10]考虑了部分可信实体的完整性哈希值被请求的频率可能会高于其他可信实体的应用场景，但当可信实体被请求的频率动态变化时该算法显得无能为力。为了改善这种情况，又构造了动态Huffman树平台配置远程证明算法[11]，但随着用户计算机软件的不断增长，Huffman树的体积也会不断膨胀，最终可能导致完整性度量与验证效率的降低。基于此，本文利用组签名算法[12]，对可信实体的哈希值采用基于组的管理方式，在RAMT方案的基础上，构造一种基于可动态调整的非平衡Merkle哈希树的平台配置远程证明机制。

2 GSRAMT：基于组签名的RAMT机制

2.1 体系结构

GSRAMT的体系结构如图1所示。尽管GSRAMT的体系结构与RAMT和IMA方案的体系结构极其相似，但因为树为非平衡Merkle哈希树且树中结点所存储的是可信实体组的公钥的哈希值，所以在可信实体的完整性度量、验证及TPM的使用等方面存在很大的差异。

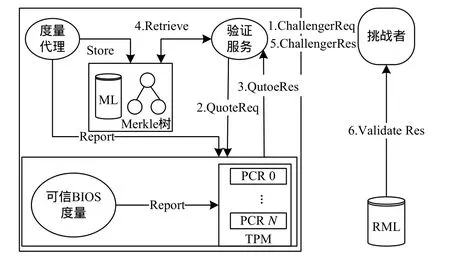
图1 G SRAMT的体系结构

2.2 符号的定义

为了叙述方便，定义以下符号：

(1)软件组：表示属于同一软件分组的软件集合，记为：

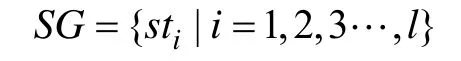
(2)软件组集：由软件组SG构成的集合，记为：

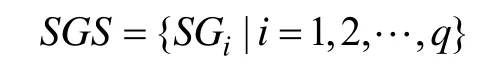
(3)树中节点的数据结构：

id：当node为叶子节点时用于标识可信实体，当node为中间节点时该值取空，即没有任何意义，当取值为NYN时表示新节点的插入位置。

weight：表示节点的权重，此处定义为相应可信实体的完整性值被请求的次数(实际上很容易被归一化为概率值)。

number：节点的编号。

block：表示块号，即相同权重节点的组编号。

hvalue：当节点为叶子节点时表示可信实体的散列值，当节点为中间节点时表示其所有孩子节点散列值连接后的再散列值。

lchild, rchild, parent：分别表示当前节点的左孩子、右孩子和父亲节点。

(4)组密钥生成算法：

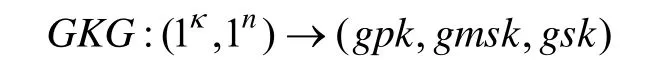
其中，κ是一个安全输入参数；n表示组中成员的个数；gpk是组公共密钥；gmsk是组管理秘密密钥；gsk表示一个长度为n的签名密钥向量，成员i被分配签名密钥gsk[ i]。

(5)组签名算法：

成员i输入消息m和自己的签名密钥gsk[ i]，即可获得消息m在签名密钥gsk[ i]作用下的签名。

(6)组签名验证算法：

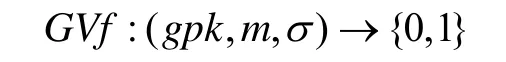
输入给定的消息、组公共密钥和消息的签名，仅当σ是m的签名时返回1，否则算法返回0。

(7)公开签名者身份算法：

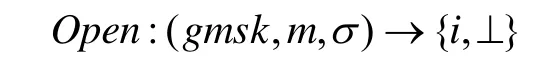
输入给定的消息、消息的签名和组管理秘密密钥，仅当σ是m的签名时返回i，否则返回⊥。

(8)组加入算法：

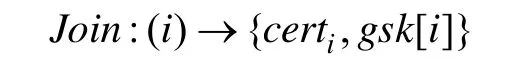
输入成员信息，算法在成功执行后，组成员会获得组成员证书和组成员签名密钥。

2.3 软件分发算法

算法1软件分发算法

Step1 令i=1，对SGi∈SGS执行组密钥生成算法GKG:(1κ,1l)→(gpk, gmsk, gsk )，获得一对组公共密钥、组管理密钥、组成员签名密钥矢量，同时将gpk写入可信实体完整性度量值参考列表RML。

Step2 令j=1，对stj∈SGi首先执行组加入算法Join: (j)→{certj, gsk[ j ]}，然后执行mj=SHA-1×(stj)，最后执行组签名算法GSig:(gsk[ j], mj)→σj(mj)，σj(mj) 和gpk随stj发布。

Step3 令j++，当j≤l时，循环执行组加入算法Join: (j)→{certj,gsk[ j ]}，然后执行mj=SHA-1×(stj)，最后执行组签名算法GSig:(gsk[ j],mj)→σj(mj)，σj(mj)随stj一起发布。

Step4 令i++，当i≤q时，对sgi∈SGS执行组密钥生成算法GKG:(1κ,1l)→(gpk, gmsk, gsk )，获得一对组公共密钥、组管理密钥、组成员签名密钥矢量，同时将gpk写入可信实体完整性度量值参考列表RML后，返回Step2，否则结束。

2.4 完整性度量算法

算法2完整性度量算法

Step1 当可信实体st被装载前首先依据公式m=SHA-1×(st)获得m的值。

Step2 执行组签名验证算法

GVf:(gpk, m,σ)→{0,1}，算法返回1时，执行gpk'= SHA-1×(gpk )，否则算法结束。

Step3 将(st, gpk')写入度量列表。

Step4 创建新节点ln, rn

Step5 若当前节点是根节点则结束，否则令：

Step6 遍历所有与curnode处于同一块中的节点，寻找同一块中节点编号最大的节点maxnode：

(1)若maxnode与curnode一致：根据孩子节点的散列值，更新当前节点的散列值并执行curnode.weight++后返回Step5。

(2)若maxnode与curnode不一致：首先交换2个节点的位置并交换2个节点的编号后令curnode.weight++，并更新当前节点的散列值，同时递归重新计算maxnode到根节点的子树中所有节点的散列值后返回Step5。

Step7 扩展根节点的散列值到PCR寄存器。

更新一个节点的算法与增加一个新节点的算法非常相似，所不同的是在Step4寻找到该节点。

2.5 完整性验证算法

GSRAMT的远程验证过程如图2所示，图中粗箭头不代表执行的步骤和信息的流向，仅用于解释ML和RML的内容，具体算法细节可参见文献[12]。

图2 G SRAMT的远程验证过程

3 算法分析

3.1 验证效率

由文献[5]可以知道，RAMT的验证效率为O( NlbN)，GSRAMT方案的验证效率为WT=O(( n/ N)lbn)，具体的证明可以参见文献[11]。因此，本文方案进一步提高了验证效率。而且分组思想的采用极大地减少了树中的节点数量。

3.2 隐私保护能力

IMA方案的远程证明需要将被验证方的所有软件配置信息提交到证明方，这种做法无疑将被验证平台的操作系统级及配置信息泄露给了远方。RAMT方案采用基于认证路径的做法，掩盖了被验证方的环境信息(仅泄露了一个节点的信息)。GSRAMT方案仍然延用了基于认证路径的远程验证方法。尽管在证明过程中，被证明方也需要整个度量日志列表提交到证明方，但该列表中的条目是软件组的公钥的哈希值，所以并没有泄露被验证平台的环境信息。而且，RAMT方案仅比对1个叶子节点的信息。因此，由其他叶子节点生成的中间节点的可信性无法校验。从这个角度看，GSRAMT方案具有比较优势。

3.3 可伸缩性

采用软件分组思想可以有效地减少Merkle树的节点数量，而且组可以大页可以小，既可软件供应商分组，也可按软件的类别分组，还可以按软件版本分组，当然一个软件也能够作为一组。因此，从这个角度来看，新机制不仅进一步提高远程证明算法的可伸缩性，而且增强了算法的灵活性。

4 结束语

本文利用组签名算法及动态Huffman树平台配置远程证明方案，在RAMT方案的基础上，提出了一种可动态调整的非平衡 Me rkle H ash树的远程证明机制。分析结果证明，该机制缩短了认证路径的长度，减少了树中节点的数量，增强了方案的隐私保护能力。下一步将主要研究该机制在基于Tomcat的Web应用中的具体实现。

[1] Paul E. Pr actical T echniques for Operating System Attestation[C]//Proceedings of the 1st I nternational Conference on Trusted Computi ng and Trust in Information T echnologies. Villach, Austria: Springer-Verlag, 2008: 258-264.

[2] Sailer R, Zhang X L, Jae ger T, et al. Design and Implementation of a TCG-based Integrity Measurement Architecture[C]// Proceedings of the 13th USENIX Security Symposium. San Diego, USA: [s. n.], 2004: 168-175.

[3] Jaeger T, Sailer R, Shankar U. P RIMA: Policy Re duced Integrity Measurement Architecture[C]//Proceedings of the 11th ACM Sy mposium on Access Co ntrol Models and Technologies. New York, USA: ACM Press, 2006: 336-345.

[4] Alsouri S, Dagdelen O, Katzenbeisser S. Group-based Attestation: Enha ncing Privacy and Man agement in Remote Attestation[C]//Proceedings of the 3rd Internatio nal Conference on Trust and Trustworthy Computing. Berlin, Germany: Springer-Verlag, 2010: 541-547.

[5] 徐梓耀, 贺也平, 邓灵莉. 一种保护隐私的高效远程验证机制[J]. 软件学报, 2011, 22(2): 339-352.

[6] Gu Liang, Ding Xuhua, Deng Huijie, et al. Remote Attestation on Program Execution[C]//Proceedings of 2008 ACM Workshop on Scalable Trusted Computing. New York, USA: ACM Press, 2008: 165-178.

[7] Peng Guojun. Dynamic Trustiness Authentication Framework Based on Software’s Behavior Integrity[C]//Proceedings of the 9th International Conference on Young Computer Scientists. Zhangjiajie, China: [s. n.], 2008: 266-271.

[8] Loscocco P A, W ilson P W, Pendergrass J A, et al. Linux Kernel Integrity Measurement Using Contextual Inspection[C]// Proceedings of t he 2nd ACM Workshop on Scalable Trusted Computing. New York, USA: ACM Press, 2007: 158-164.

[9] 谢海涛, 王玉明, 杨宗凯, 等. 自适应Huffman树组密钥更新方案[J]. 华中科技大学学报: 自然科学版, 2009, 37(9): 33-36.

[10] 付东来, 彭新光, 陈够喜, 等. 一种高效的平台配置远程证明机制[J]. 计算机工程, 2012, 38(7): 25-27.

[11] 付东来, 彭新光, 陈够喜, 等. 动态Huffman树平台配置远程证明方案[J]. 计算机应用, 2012, 32(8): 2275-2279, 2282.

[12] Sun Y ipin, Fen g Zhe nqian, Hu Qiaolin. An Ef ficient Distributed Key Manag ement S cheme for Group-signature Based Anonymous Authentication in VANET[J]. Security and Communication Networks, 2012, 5(1): 79-86.

编辑 索书志

An Improved Platform Configuration Remote Attestation Mechanism of Group Signatures

LI Hong-yu1, FU Dong-lai2

(1. Network Center, Shanxi Finance & Taxation College, Taiyuan 030024, China; 2. Institute of Electronics and Computer Science & Technology, North University of China, Taiyuan 030051, China)

In order to improve efficiency, privacy protecting and scalability of remote attestation, a new method to measure the integrity of trusted entities is proposed. The method based on Remote Attestation based on Merkle Hash Tree(RAMT) takes the frequency of trusted entities into account. It leverag es multiple techniques including group signatures a nd dyn amic Huffman algorithms. Thus, it red uces dramatically storage space to store measurement log of executables and hides information of specific software and cuts down a length of the path of verification. These algorithms including software distribution, integrity measurement and verification are given and their advantages are described from three aspects including verification efficiency, privacy protection and scalability. Analysis shows the abil ity of the protection privacy is enhanced. The efficiency and the scalability of the remote attestation are improved highly.

trusted computing; remote attestation; group signature; Merkle Hash tree; privacy protection; scalability

10.3969/j.issn.1000-3428.2014.05.021

山西省科技攻关计划基金资助项目(20090322004)；中北大学自然科学基金资助项目(2013)。

李宏宇(1979－)，男，硕士，主研方向：网络信息安全，可信计算；付东来(通讯作者)，讲师、博士研究生。

2012-12-13

2013-04-04E-mail：lihongyusx@163.com

1000-3428(2014)05-0099-04

A

TP309