基于物理干扰模型的WSN拓扑控制算法

李玉民，禹继国，万胜利

(曲阜师范大学计算机科学学院，山东 日照276826)

基于物理干扰模型的WSN拓扑控制算法

李玉民，禹继国，万胜利

(曲阜师范大学计算机科学学院，山东 日照276826)

拓扑控制是无线传感器网络研究中的重要问题。现有的大多数关于拓扑控制的工作集中于如何降低能耗，但是没有考虑干扰带来的影响。针对网络容量的最大化问题，提出一种在信号干扰信噪比模型下的拓扑控制算法PLTCA。该算法无需任何节点的位置信息，通过计算3跳以内的前向和后向列表来构建拓扑。在PLTCA算法中，采用功率控制技术，节点通过改变发射功率或者发射方向选择自己的邻居节点，从而控制网络拓扑结构。通过理论分析对算法的连通性进行论证。仿真结果表明，PLTCA算法在保证网络连通性的基础上，减少了网络总体的能量损耗，与MaxSR算法相比，节点的平均链路能量损耗减少10%～20%。

无线自组网；信号干扰信噪比；无线传感器网络；拓扑控制；能量损耗；连通性

1 概述

无线传感器网络(Wireless Sensor Net work, WS N)有着广阔的应用前景，它在国家安全、环境监测、交通管理、空间探索等领域有着重大的应用价值，引起了各界的广泛关注。拓扑控制技术是无线传感器网络中最重要的技术之一。在由无线传感器网络生成的网络拓扑中，可以直接通信的2个节点之间存在一条拓扑边。如果没有拓扑控制，所有节点都会以最大无线传输功率工作。网络中每个节点的无线信号将覆盖大量其他节点，造成无线信号冲突频繁，影响节点的无线通信质量，降低网络的吞吐率。另一方面，在生成的网络拓扑中将存在大量的边，从而导致网络拓扑信息量大，路由计算复杂，浪费了宝贵的计算资源。因此，需要研究无线传感器网络中的拓扑控制问题，在维持拓扑某些全局性质的前提下，通过调整节点的发送功率来延长网络生命周期，提高网络吞吐量，降低网络干扰，节约节点资源。

在无线传感器网络中，如何在消耗最低功率的前提下确定每个节点的传输功率以维持网络连通性，提高空间重用是一个重要的问题[1]。文献[2]提出一种拓扑控制算法RTC。该算法基于RSSI均值计算节点间双向路径损耗，从而判断两节点间是否存在每跳通信链路代价都小于直接通信链路代价的两跳路径，以构建局部优化拓扑。

本文提出一种集中式算法，该算法是一种基于物理模型的拓扑控制算法(Path Lo ss Topology C ontrol Al gorithm, PLTCA)。

2 相关工作

无线传感器网络通常具有大规模、自组织、随机部署、传感器节点资源有限、网络拓扑时常发生变化的特点[3]。这些特点反映了拓扑控制问题的重要性。拓扑控制的目标是维持无线自组网的性能(例如，连通性和功率效率)。在现存的拓扑控制算法中文献[4]做了一个全面的研究。它分为2个基本的类别：链路控制[5]和节点控制[6]。在链路控制中，节点对不同的接收器使用不同的发射功率。相反，在节点控制中，节点对不同的接收器使用相同的发射功率。节点控制简化了邻居的管理和相关的MAC控制，链路控制会节省很多能量。为了在有损耗的无线传感器网络中实现可靠的拓扑，提出了ATPC算法设计，仅仅是为了维持每跳的链路质量[7]。它不能在多跳网络上实现路径质量的需求，也不能给不同的质量标准灵活地配置一个网络。在文献[8]中，ART协议是在室内环境中基于链路测量值的拓扑控制。在另一方面，实验中的结果通过采用CTC维持现实的和真实的链路模型。文献[9]研究了传统网络模型的局限性，并且在物理模型下分析了拓扑控制中链路调度的影响。文献[10]提出局部算法。文献[11]提出一种面向实际无线环境应用且无需任何位置信息的拓扑控制算法。本文提出的算法是基于物理干扰模型的拓扑控制算法。

3 WSN的干扰模型和网络模型

3.1 物理干扰模型

大规模的路径损耗被用来描述信号是如何沿着传输路径变弱的。让gu, v作为节点vi到节点vj的通道增益(它通常假设为恒定的互不依靠的距离)，接收功率表示为：

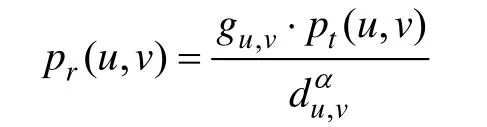
其中，α是路径损耗指数，α的价值范围在2～4之间，取决于使用的传播模型(例α=2是自由空间模型)。一个传输活动是否成功取决于2个因素，也就是接收灵敏度和信号干扰信噪比(Signal to Interference plus Noise Ratio, SINR)。具体地说，是让RXmin作为接收器的临界值来正确地解码接收信号，SINR的临界值为β。一个信号可以成功地接收和解码只要满足以下2个公式：

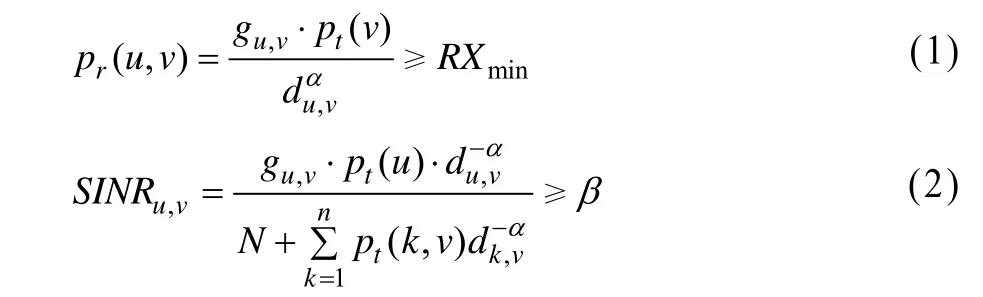
3.2 无线传感器网络模型

在无线传感器网络中假设每个节点u(u∈V)的最大发射功率pmax。无线传感器网络中的任意节点u是有向图G( V, E)的顶点，图G中的节点u和v通过一条从u到v的边连接。如果(u, v)∈E，则(v, u)∈E，G为所有节点以最大功率发射生成的初始拓扑图。在图G( V, E)中，pmin(u, v)表示节点u到达邻居节点v的最小功率，此时v的接收信号强度为rssv。用CG(u, v)表示节点u以功率pmin(u, v)发射时的路径损耗，并将CG(u, v)作为权值赋给边(u, v)，其中(u, v)∈E。如果图G是连通的，则节点u和v之间必然存在并且至少存在一条链路：

则该链路的路径损耗可表示为：

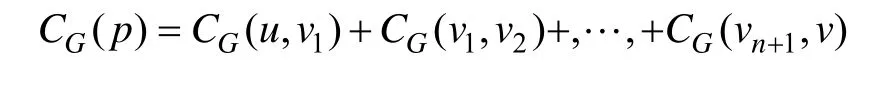
4 算法及其实现

4.1 无线传感器拓扑控制算法描述

相关定义如下：

(1)pmin(u, v)表示从节点u到达节点v所需的最小发射功率。

(2)C( u, v)表示路径损耗。对于每个有序节点对u和v，定义一个关联组C( u, v)=(α1, α2)，α1=IDv；α2= pmin(u, v)-rssv。其中，α1是节点v的编号；α2表示节点u以最小功率pmin(u, v)发射到v的路径损耗值。如果α2＜α2'或者α2=α2'且α1＜α2'，则(α1, α2)＜(α', α')。

12

(3)forwardlist和backwardlist表示路径损耗列表，也就是说前向路径损耗列表和后向路径损耗列表。forwardlist( u)记录了节点u与它的所有邻居节点直接通信的关联组C( u, v)=(α1, α2)，u, v∈V，backwardlist( u)记录了u的所有邻居节点与u直接通信的关联组C( u, v)= (α', α')，u, v∈V且v∈N( u)。其中，N( u)表示的是节

12 点u的邻居集。假设每个节点u有k个邻居节点，则它具有k个发射功率等级，其最大功率为pmax，最小功率为pmin，第k个邻居通信的发射功率为pk。各节点依次以计算好的功率pk广播包含当前发射功率pk和节点ID的HELLO报文，每个节点根据接收的报文编制前向和后向路径损耗列表。

算法描述如下：

Step1 节点u在初始时以最大功率工作，并广播探测拓扑的请求信息，请求信息中包含节点的ID、节点的位置和最大功率等信息。节点v收到请求信息后，判断是否大于最小接收功率。根据SINR物理模型判断v是否能够接收u的消息。如果节点v能收到u的消息，则将v加到N( u)中。

Step2 确定k个发射功率，每个节点以设定的最大功率广播自身的ID号和位置信息。根据接收者的消息通过式(1)确定k个发送功率。

Step3 列表汇集，各节点依次以功率pk广播包含当前发射功率pk和节点ID的HELLO报文，每个节点根据接收的报文编制前向路径损耗列表和后向路径损耗列表。

Step4 拓扑建立，每个节点以最大发射功率pmax向它的所有邻居节点广播前向和后向路径损耗列表，同时也收集其各个邻居节点的前向和后向路径损耗列表。计算节点u和v之间小于等于3跳的前向和后向路径，并判断每一跳的能量消耗是否比节点u和v直接通信所需能量消耗小。如果u和v之间存在这样的路径，则从图G中移走边G( u, v)。

4.2 伪代码

算法主要由4个阶段组成：邻居生成阶段，功率分配阶段，列表汇集阶段和拓扑建立阶段。

(1)邻居生成阶段

(2)功率分配阶段

假设每个节点u具有k个功率等级，其最大功率为pmax，最小功率为pmin，且当前级别功率用pk表示，每个传感器节点的最小接收功率假设为0.4。

伪代码如下：

(3)列表汇集阶段

各节点依次以功率pk广播包含当前发射功率pk和节点ID的HELLO报文，每个节点根据接收的报文编制前向和后向路径损耗列表。该过程的程序伪代码如下：

(4)拓扑建立阶段

每个节点以最大发射功率pmax向它的所有邻居节点广播它的前向路径损耗列表和后向路径损耗列表，同时也收集其各个邻居节点的前向路径损耗列表和后向路径损耗列表。从任一节点u的前向路径损耗列表中取出第一个有序对C( u, v)，并将C( u, v)从forwardlist( u)中删除。构建一个节点v的所有邻居节点中满足C( w, v)＜C( u, v),w∈N( v)的节点集合Nu(v)。从Nu(v)中任意取出ω，先判断ω是否为u的邻居节点。如果是，则判断C( u,ω)＜ C( u, v)是否成立，如果成立，则标志变量ftPath=True；如果ω不是u的邻居节点，判断是否存在u的邻居节点z满足条件：(C( u, z)∈forwardlist( u))&&(C( z,ω)forwardlist( z) ), z∈N( u)and z≠v 。如果成立，则ftPath= True。同样，可以判断是否存在从v到u的3跳或者3跳内的后向路径，并且每一跳的能量消耗都小于直接从v到u的路径消耗。如果前向和后向存在这样的路径，则从图中删除边(u,v)，该过程的程序伪码如下：

4.3 网络连通性分析

定理 如果初始图G( V, E)连通，则执行算法得到的拓扑图G'( V',E')也是连通的。

证明：对于任意2个节点u, v∈V，由于图G( V, E)是连通的，因此图G( V, E)中节点u，v之间存在路径p，设路径p为：p={v0=u, v1, v2,…,vn=v}。其中，vi-1和vi( i=0,1,…,n)互为邻居节点。假设节点之间的通信是满足双向性的，仅考虑前向路径损耗。证明图G'( V',E')是连通的，只需证明在执行完算法后，任意2个互为邻居的节点vi-1和vi( i=0,1,…,n)之间是存在通信链路的。执行算法后，G'( V',E')中每个节点v都建立起了自己的前向路径损耗列表forwardlist(vi)并且收集了邻居节点的后向路径损耗列表backwardlist(vi+1)，如果2个节点是邻居，则前向路径损耗列表forwardlist(vi)中一定存在C( vi, vi+1)。因此，只需证明vi和vi+1之间存在通信链路。假设执行算法后vi和vi+1之间不存在通信链路，则边e( vi, vi+1)一定不存在。根据算法的执行规则，在节点vi+1的后向路径损耗列表backwardlist(vi+1)中存在C(ω,vi +1)，在集合Nv(vi+1)中一定存在满足C(ω,vi +1)＜C( vi, vi+1)的节点ω。那么分为以下2种情况：

(1)节点vi的前向路径损耗列表forwardlist(vi)中有C( vi,ω)＜C( vi, vi +1)，ω为vi和vi+1的邻居，且在vi和vi+1之间存在C( v,ω)＜C(ω,vi+1)，也就是说节点vi和节点vi+1之间存在通信链路vi→ω→vi+1。

(2)在节点vi的前向路径损耗列表forwardlist(vi)中存在C( vi, z), z∈N( vi)，在z的前向路径损耗列表forwardlist(z)中存在C( z,ω)，且满足max(C( u, z), C( z,ω))＜C( vi, vi +1)，可见在vi和vi+1之间存在C( vi, z)＜C( z,ω)＜C( z, vi +1)，即vi和vi+1之间存在通信路径vi→z→ω→vi+1。因此，vi和vi+1之间存在通信链路，与前边的假设是相互矛盾的。所以如果初始图G( V, E)连通，则执行算法得到的拓扑图G'( V',E')也是连通的。

5 仿真结果分析

PLTCA采用路径损耗构建网络拓扑，且无需节点的位置信息。运用Java仿真器对PLTCA算法与MaxSR算法进行了对比仿真。

在实验中，路径损耗指数α在整个网络中是相同的，取α=2。节点的发射功率是通过路径损耗模型计算的，基于这种参数配置，提出了以下仿真：

方案1 将50个节点随机布置在500×400的区域内，每个节点赋予唯一的ID号。执行PLTCA算法得到的拓扑结构与执行MaxSR[13]算法得到的拓扑结构进行了对比，如图1和图2所示。其中，MaxSR算法执行后链路数为52，执行PLTCA算法后链路数为49。

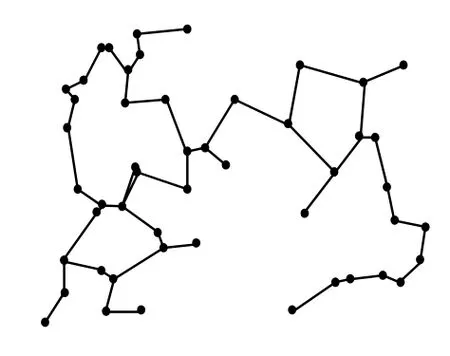
图1 P LTCA算法的执行结果1

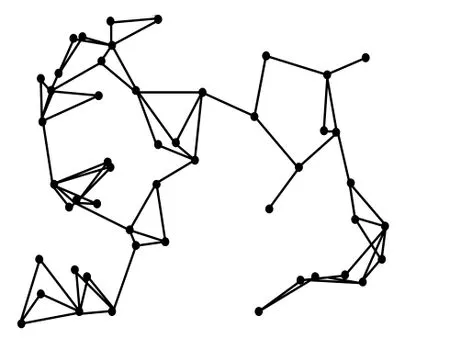
图2 MaxSR算法的执行结果1

方案2 将80个节点随机布置在500×400的区域内，每个节点赋予唯一的ID号。执行PLTCA算法得到的拓扑结构与执行算法MaxSR的拓扑结构进行对比，如图3和图4所示。其中，MaxSR算法执行后链路数为93，执行PLTCA算法后链路数为82。

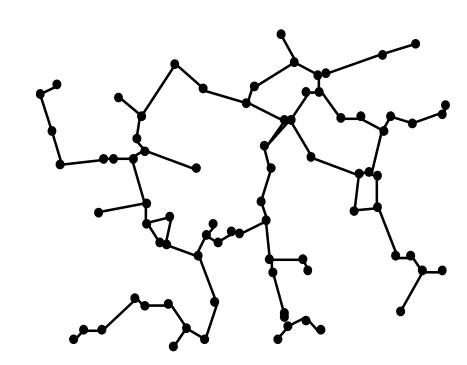
图3 P LTCA算法的执行结果2

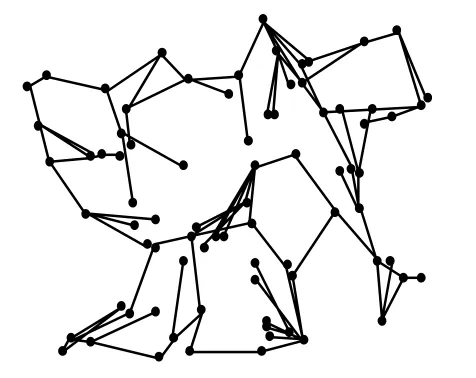
图4 MaxSR算法的执行结果2

方案3 将110个节点随机布置在500×400的区域内，每个节点赋予唯一的ID号。执行PLTCA算法得到的拓扑结构与执行算法MaxSR的拓扑结构进行了对比，如图5和图6所示。其中，MaxSR算法执行后链路数为132，执行PLTCA算法后链路数为121。

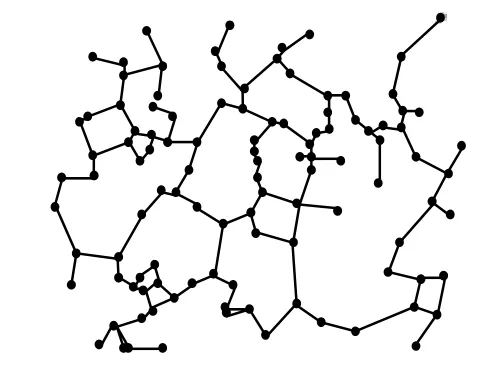
图5 L TCA算法的执行结果3

图6 MaxSR算法的执行结果3

图7、图8为在相同的传感器节点部署条件下，分别对激活链路数和平均链路路经损耗进行了对比，其中，激活的链路指的是拓扑图中的链路数，平均链路路经损耗指的是所有链路路经损耗的和除以链路数。

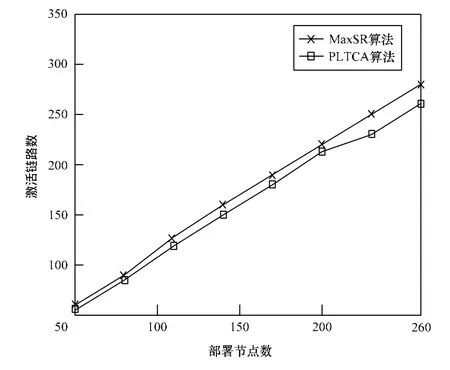
图7 激活链路数对比

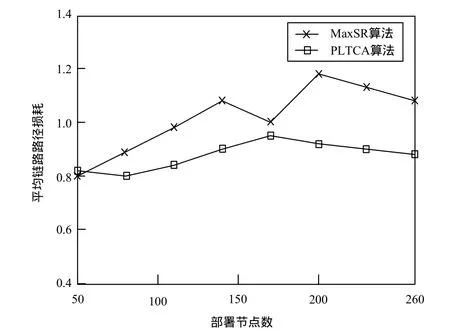
图8 平均链路路径损耗对比

通过以上仿真实验，对2个算法的性能结果进行了比较。结果表明，算法PLTCA的性能较为优越，算法PLTCA在节点的平均链路路径损耗上优于MaxSR算法10%～20%。物理模型下研究拓扑控制更接近真实情况。

6 结束语

实际的无线环境中具有多种不规则和多径传播现象，如果没有拓扑控制算法，无线传感器网络节点将被迫使用大发射功率发送信息以确保通信和网络连通。本文提出的算法并不需要任何基于位置的信息，适用于实际无线环境下的普通节点、异构网络，减少了网络总体能量消耗，延长了网络生命周期。仿真结果表明，PLTCA算法具有较好的性能。在下一步的工作中，将进一步降低计算复杂度以及通信开销。

[1] Hu L. A Novel Topology Control for Multihop Pac ket Radio Networks[C]//Proc. of IE EE INF OCOM’91. Mia mi, US A: [s. n.], 1991: 1084-1093.

[2] 王出航. 基于RSSI均值的无线传感器网络拓扑控制算法[J].计算机应用, 2012, 32(2): 352-354, 358.

[3] Akyildiz I F, Su W eilian, Sankarasubramaniam Y, et al. A Survey on Sensor Networks[J]. IEEE Communications Magazine, 2002, 40(8): 102-114.

[4] Simon G. Probabilistic Wireless Network Simulator[EB/OL]. (2008-06-23). http://www.isis.vanderbilt.edu/projects/nest/prowler.

[5] Ramanathan R, Hain R. Topology Co ntrol of Multihop Wireless N etworks U sing T ransmit Pow er A djustment[C]// Proc. of IEEE INFOCOM’00. [S. l.]: IEEE Press, 2000: 404-413.

[6] Li Xiangyang, Song Wenzhan, Wang Yu. Localized Topology Control for Heterogeneous W ireless Sensor Networks[J]. ACM Transactions on Sensor Networks, 2006, 2(1): 129-153.

[7] Lin Shan, Z hang Jingbin, Zh ou Gang, et al. A TPC: Adaptive Transmission Power Control for Wireless Sensor Networks[C]// Proc. of the 4th International Conference on Embedded Networked Sensor Systems. Ne w York, US A: ACM Press, 2006: 223-236.

[8] Hackmann G, Chipara O, Lu Chenyang. Robust Topology Control for Indoor Wireless Sensor Networks[C]//Proc. of the 6th International Conference on Embedded Networked Sensor Systems. Raleigh, USA: [s. n.], 2008: 57-70.

[9] Moscibroda T, Wattenhofer R, Zollinger A. Topology Control Meets SINR: The Scheduling C omplexity of A rbitrary Topologies[C]//Proc. of the 7th In ternational Symposium on Mobile Ad Hoc Networking and Computing. New York, USA: ACM Press, 2006: 310-321.

[10] Gao Jie, Gu ibas L J, Hershberger J, et al. Ge ometric Spanner for Routing in Mobile Networks[C]//Proc. of the 2nd ACM Symposium on Mobile Ad Hoc Networking and Computing. [S. l.]: ACM Press, 2001: 45-55.

[11] 王出航, 王志军. 基于路径损耗的WSN拓扑控制算法[J].计算机工程, 2011, 37(23): 102-104.

[12] Cardieri P. Modeling Interference in Wireless A d Hoc Networks[J]. IE EE Communicat ions Surveys & T utorials, 2010, 12(4): 551-572.

[13] Gao Yan, Ho u J C, Nguyen H. Topology Control for Maintaining Network Connectivity and M aximizing Network Capacity Under the Physical Model[C]//Proc. of the 27th Conference on Computer Communications. [S. l.]: IEEE Press, 2008: 1013-1021.

编辑 顾逸斐

Topology Control Algorithm for WSN Based on Physical Interference Model

LI Yu-min, YU Ji-guo, WAN Sheng-li

(Computer Science College, Qufu Normal University, Rizhao 276826, China)

Topology control is an important issue in Wireless Sensor Network(WSN) research. Most of the existing work on topology control focus on how to reduce energy consumption, but they do not consider the effects of interference. This paper proposes the topology control algorithm PLTCA under physical Signal to Interference plus Noise Ratio(SINR) model, with the objective of maximizing network capacity problem. It constructs topology through computing forward and backward list within three or fewer hops. In PLTCA, power control technology is used and each node can choose their own neighbors by changing the direction of the transmission or the transmission power, so as to control network topology structure. Theoretical analysis sh ows the co nnectivity of the links. This paper proposes a ce ntralized approach, called PLTCA. Simulation results show that the algor ithm can guarantee the network connectivity and decrease the energy dissipation of the network. PLTCA is shown to be superior to the MaxSR algorithm by 10%～20% on the average energy loss of links.

Ad hoc network; Signal to Interference plus Noise Ratio(SINR); Wireless Sensor Network(WSN); topology control; energy loss; connectivity

10.3969/j.issn.1000-3428.2014.05.019

国家自然科学基金资助项目(11101243)；山东省自然科学基金资助项目(ZR2012FM023, Z R2012FQ011)；山东省高校科技计划基金资助项目(J10LG09, J12LN06)。

李玉民(1988－)，男，硕士研究生，主研方向：无线网络；禹继国，教授、博士；万胜利，硕士研究生。

2013-04-16

2013-05-17E-mail：liyumin01@126.com

1000-3428(2014)05-0089-05

A

TP301.6