基于多变异个体的多目标差分进化改进算法

沈佳杰，江 红，王 肃

(华东师范大学信息科学技术学院，上海 20024 1)

基于多变异个体的多目标差分进化改进算法

沈佳杰，江 红，王 肃

(华东师范大学信息科学技术学院，上海 20024 1)

针对多目标差分进化算法在高维函数下收敛速度慢和易早熟的问题，提出一种基于多变异个体的多目标差分进化改进算法。通过在多目标差分进化算法的个体变异及交叉操作中，引入多个变异个体，使得在高维多目标函数情况下，多目标差分进化算法种群可以更好地保持多样性，减少种群陷入局部最优解的可能性，从而提高该算法在高维多目标优化问题环境下，最优值解的搜索速度及全局最优值解的查找能力。实验结果表明，在高维多目标环境下，与标准多目标差分进化算法相比，该算法可以更快速地找到多个目标函数组的非劣最优值解集。

多目标优化问题；差分进化算法；多变异个体；计算智能；最优值搜索；迭代速度

1 概述

差分进化[1](Differential Evolution, DE)算法作为一个具有良好性能的优化算法[2]，在优化领域得到广泛的应用，具有出色的性能表现，所以已有许多学者对其进行了研究，如使用领域内的信息进行算子的改进[3]、在差分进化算法中使用采样排序[4]、加入自适应概念[5]以及引入极大熵的概念[6]。差分进化算法的综述还可以参考文献[7-8]。在多目标环境下，如何提高其算法性能成为一个研究的热点，也有不少研究者对此问题提出了改进方案，如在多目标算法中加入混沌理论对多目标差分进化算法进行分阶段二次变异改进[9]、直接将混沌理论与差分进化算法结合[10]、在多目标差分进化算法中引入双群体[11]、基于Pareto解的性质改进差分进化算法[12]及直接将差分进化算法应用于多目标问题等；利用非劣最优值的性质对差分进化算法进行改进，从而使其能够对于多目标问题求解[13]及使用基于非劣最优值竞争、排序的方法改进差分进化算法，将差分进化算法应用于多目标问题[14]。对于多目标问题本身也有很多不同的探讨，如文献[15]对主要的多目标算法进行综述和总结，文献[16]对于多目标算法的概念、理论以及应用场景进行了综述，文献[17]对于多目标算法的收敛性进行了研究。

本文提出一种基于多变异个体的多目标差分进化改进算法，引入多个变异个体，在交叉操作生成实验个体的过程中，对不同的个体引入不同交叉概率，通过多个变异个体交叉生成实验个体。

2 标准DE、多目标问题描述及标准多目标DE

2.1 标准差分进化算法

差分进化算法是基于群体智能的进化算法，其主要的操作有变异操作、交叉操作和选择操作，通过这3种不同操作，标准的差分进化算法[1-2]可以高效地找出函数的最优值，其主要定义如下：

个体种群由N个独立的个体组成，记为：

其中，N为种群数。每一个个体是一个D维向量，记为：

其中，D为问题维数。

类似于遗传算法，需要通过差分进化算法中的变异、交叉和选择操作对种群进行变换，从而找出最优值点。

2.1.1 变异操作

变异操作的主要作用是对不同个体进行差分变换，从而产生新的变异个体。变异公式为：

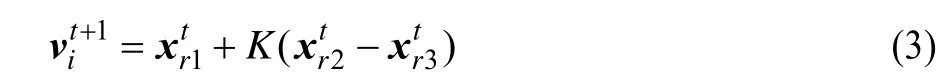
i通过式(3)计算而得。

2.1.2 交叉操作

交叉操作的主要作用是生成的实验个体与原个体进行交叉操作，从而生成新的变异个体。交叉操作为：

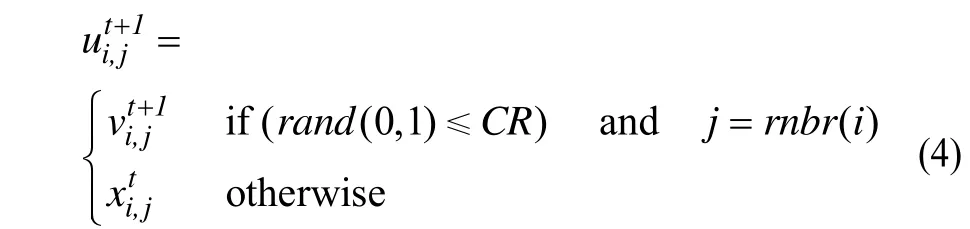
其中，rand(0,1)为(0,1)之间随机数；CR为交叉概率，其取值在[0,1]之间；rnbr( i)是指第i个个体的向量标号。

如式(4)所示，交叉操作的本质是将变异个体与原个体在各个维度向量上以一定概率进行交叉，生成新的实验个体ui。

2.1.3 选择操作

选择操作的主要作用是在个体进入下一步迭代时，在现在个体和实验个体中选择一个适应度较高的个体生成下一代的种群。选择操作为：

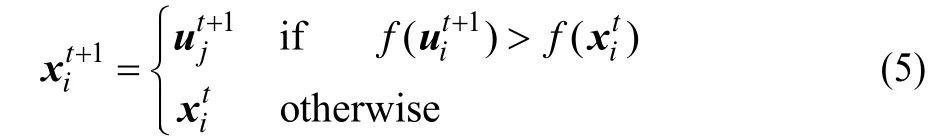
如式(5)所示，当改进实验个体的适应度大于原来个体适应度值，则采用改进后的实验个体，其他情况下采用原来个体。

2.1.4 标准差分算法

标准的差分进化算法步骤如下：

步骤1初始化种群X0进入差分进化算法，确定CR，将迭代步数t设为1，同时设定最大迭代步数tmax。

步骤3调用交叉操作。通过式(4)，生成所有个体的实验个体uit+1。

步骤4调用选择操作。通过式(5)，判断生成的实验个体是否比现存个体的适应度高，如果适应度高于现存个体，则让实验个体uit+1代替当前个体xit；否则保留xit，进而生成下一代个体xit+1。

步骤5判断是否达到最优值或迭代步骤数超过最大迭代步骤数，如果是，转向步骤6；否则转向步骤2。

步骤6输出最优值点。

对于传统的差分进化算法，不同学者提出了各自的改进方案，如文献[4]通过对差分进化算法中引入粒子群算法的相关概念，从而提高算法的效率。

2.2 多目标问题描述

通常多目标问题描述如下[1]：

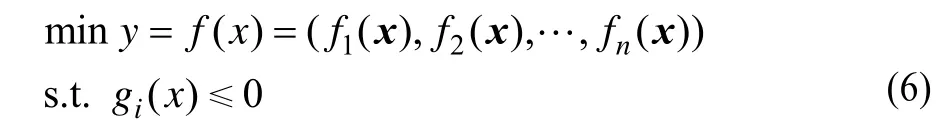
其中，决策向量x∈Rm；目标向量y∈Rn；fi( x)为目标函数；gi( x)为约束条件。

由式(6)可知，只有在有限条件下，才可使所有的目标函数达到最优值，但是存在这样的解：对于一个或多个目标函数不可能再进一步优化，而对于其他函数不可能再劣化，这样的解叫做非劣最优解。非劣最优解的定义如下[1]：

定义1若存在一个x*，使得不存在i，使得fi(x)＜fi( x*)，则称x*是非劣最优解。

定义2 由所有的非劣最优解组成的集合叫做多目标非劣最优解集。

2.3 多目标标准差分进化算法

由于标准差分进化算法只能针对于单目标问题，因此不同的研究学者对标准差分进化算法在多目标情况下进行了改进，如文献[13]提出Pareto差分进化方法(PDEA)，可以很好地维护种群的多样性，但是收敛速度较慢；文献[14]提出了多目标差分进化方法(DEMO)，虽然提高了收敛速度，但是损失了种群的多样性易陷入早熟。

本文介绍文献[10]中多目标差分进化方法(DEMO)主要步骤，相对于标准差分进化算法，文献[10]最大的改进在于重新定义每一个粒子的适应度函数和引入混沌理论。本文提到的标准差分进化算法中每个个体的适应度函数采用文献[10]种群个体的排序方法，根据个体的优劣水平和拥挤距离2个指标实现。首先找出种群中的所有非劣最优解，其优劣等级都取1，然后找出剩余个体中的所有非劣最优解，其等级都取2重复进行，直到种群所有个体都具有相应的优劣等级为止。

3 本文改进的差分进化算法

3.1 本文算法的假设及定义

本文算法的假设及定义如下：

假设1当前的最优值点有一定的概率是全局的最优值点，且非劣最优解集一般在最优值周围可以找到。

假设2个体的每一维对于每一个目标函数值的影响相对独立的。

假设3个体对于每一个目标函数值对于非劣最优值的适应度值(即个体的适应度值)的影响相对独立。

定义3当前所有的个体中对于目标函数i的最大值称为对于目标函数i的全局最优值，记为：

对于第j号个体，在第i个目标函数下的历史最优值所在的位置参数，称为第j号个体在第i个目标函数下的历史最优值位置，记为：

定义4第j个个体对于第i个函数存在一个变异个体，这个变异个体由下式计算而得[4]：

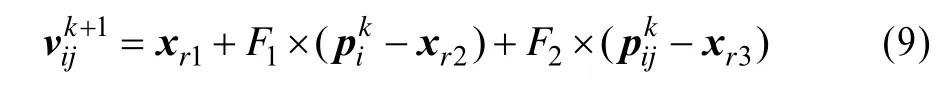
其中，当前状态下xr1，xr2，xr3是3个不同个体；F1，F2是2个缩放比例因子；pik为第k步时第i个目标函数的全局最优值；pikj为第k步时第i个目标函数第j个粒子的局部最优值。

定义5 对于每一个变异个体和原来的个体分配一个交叉概率，变异个体中每一维选中加入实验个体的概率等于其交叉概率，由多个变异个体和原个体通过交叉概率，生成实验个体，称为多变异实验体，记为：

其中，rd=rand(0,1)代表(0,1)之间的随机数；cri代表交叉概率对于每一个变异个体和原个体被选择的累计概率。对于比较重要的目标函数(即优先度较高的目标函数)，通常需要分配更高的交叉概率值。

定义6算法迭代终止时，所有目标函数当前的平均最优值减去所有目标函数的理论最优值的乘积，称为平均最优值乘积，记为：

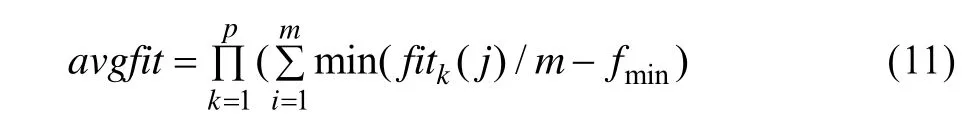
其中，fitk(j)为j号粒子在第k函数条件下的适应度；n为粒子群中粒子的个数；fmin是所有函数的最小值；m为独立实验的次数；p为目标函数的个数。

这个定义主要是为了客观评价一个多目标算法的优劣提供一个客观的标准，由以上的定义可知在对于求最小值问题，如果多目标粒子群算法的乘积平均最优值越小，则说明这个算法可以更快找到更好的优化解。

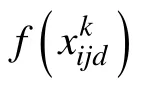
3.2 本文算法

本文算法的迭代步骤如下：

步骤1初始化多目标差分进化算法个体，对于每一个目标函数设置一个交叉概率。

步骤2根据所有个体的状态，按照式(7)、式(8)计算目标函数i下所有个体全局最优值和历史最优值位置

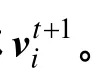
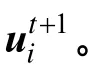
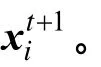
步骤6判断当前个体群是否满足多目标条件或超过最大迭代步骤数，如果是则进入步骤7，否则进入步骤2。

步骤7输出当前最优点。

3.3 本文算法性质及定理证明

本文算法的性质以及定理证明如下：

定理在有足够个体数量和迭代步骤数的条件下，变异个体找到每一个目标函数的最优值。

证明：由于个体不同的维度对于目标函数值的影响相对独立，因此如果当前个体进化为最优值，其适应度函数也会相应增加，因为每一维的变异个体有一定的概率进入实验个体，而每一个实验个体又有一定的概率变成下一代的个体且必然优于原先个体，第k+n步的生成个体i的第d维对于函数j的函数最优值的影响必然优于第k步的被选入实验个体i的第d维对于函数j的影响，即：

本文改进的多目标差分进化算法在有足够粒子数量和迭代步骤数的条件下，每一维对于目标函数最优值的影响将会单调上升，又因为每一维的目标函数值单调上升，同时每一维对于目标函数值的影响相对独立，所以本文改进的差分进化算法可以找到每一个目标函数的最优值。

推论 在有足够个体数量和迭代步骤数的条件下，本文的多目标差分进化算法可以有效地找到函数的非劣最优解集。

证明：由定理可知，本文改进的多目标差分进化算法可以找到各个目标函数的全局最优值，又因为每一个目标函数值相对独立地影响非劣最优值的适应度值，所以在有足够个体数量和迭代步骤数的条件下，个体的非劣最优值的适应度值会足够好，从而找到全局的非劣最优值。

由定理和推论可知，本文改进的多目标差分进化算法主要通过保证每一个目标函数的每一维的最优值的取得进而保证单个目标函数的最优值的取得，从而实现取得全局的多目标问题的非劣最优值。

4 实验结果与分析

实验中使用5个测试函数，如表1所示，对于这5个测试函数进行两两组合形成10个不同的测试情况。在低维(2,2,2,2,2)和高维(2,10,5,5,10)条件下，当2个函数的维数不一致时以维数小的函数维数为准，分别对4种不同的交叉概率CR(0.1, 0.2, 0.3, 0.4)，进行10次独立的实验，统计其最小迭代步骤数、最多迭代步骤数和平均迭代步骤数。对于目标值的设定，如种群同时满足2个测试函数达标值时，则认为这个测试函数已经找到函数的最优解，算法结束。

在多变异个体的情况下每一个函数的交叉概率是指每一个个体的交叉概率，在标准差分进化算法的条件下，变异个体的交叉概率等于标注交叉概率的2倍。

表1展示了5个测试函数的各项参数设定，表2展示了在低维条件下本文改进粒子群算法和文献[1]中粒子群算法迭代步骤数的比较，表3展示了在高维条件下本文改进粒子群算法和文献[1]中粒子群算法迭代步骤数的比较。其中，SDE代表标准的多目标差分进化算法，IDE代表本文改进的多目标粒子算法。

表1 实验测试函数

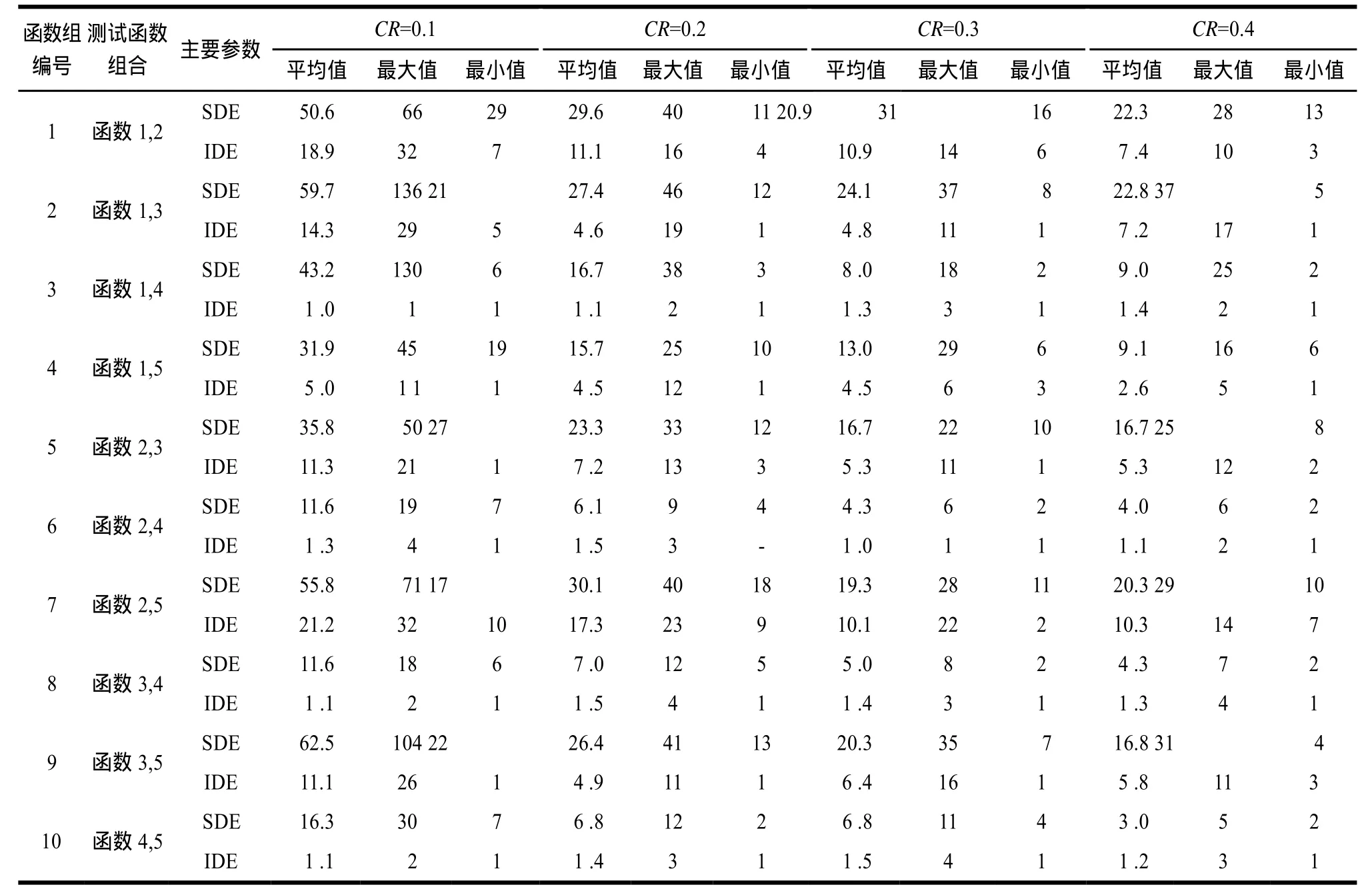
表2 低维条件下(2,2,2,2,2)5个基本函数组合改进前后的迭代步骤数比较

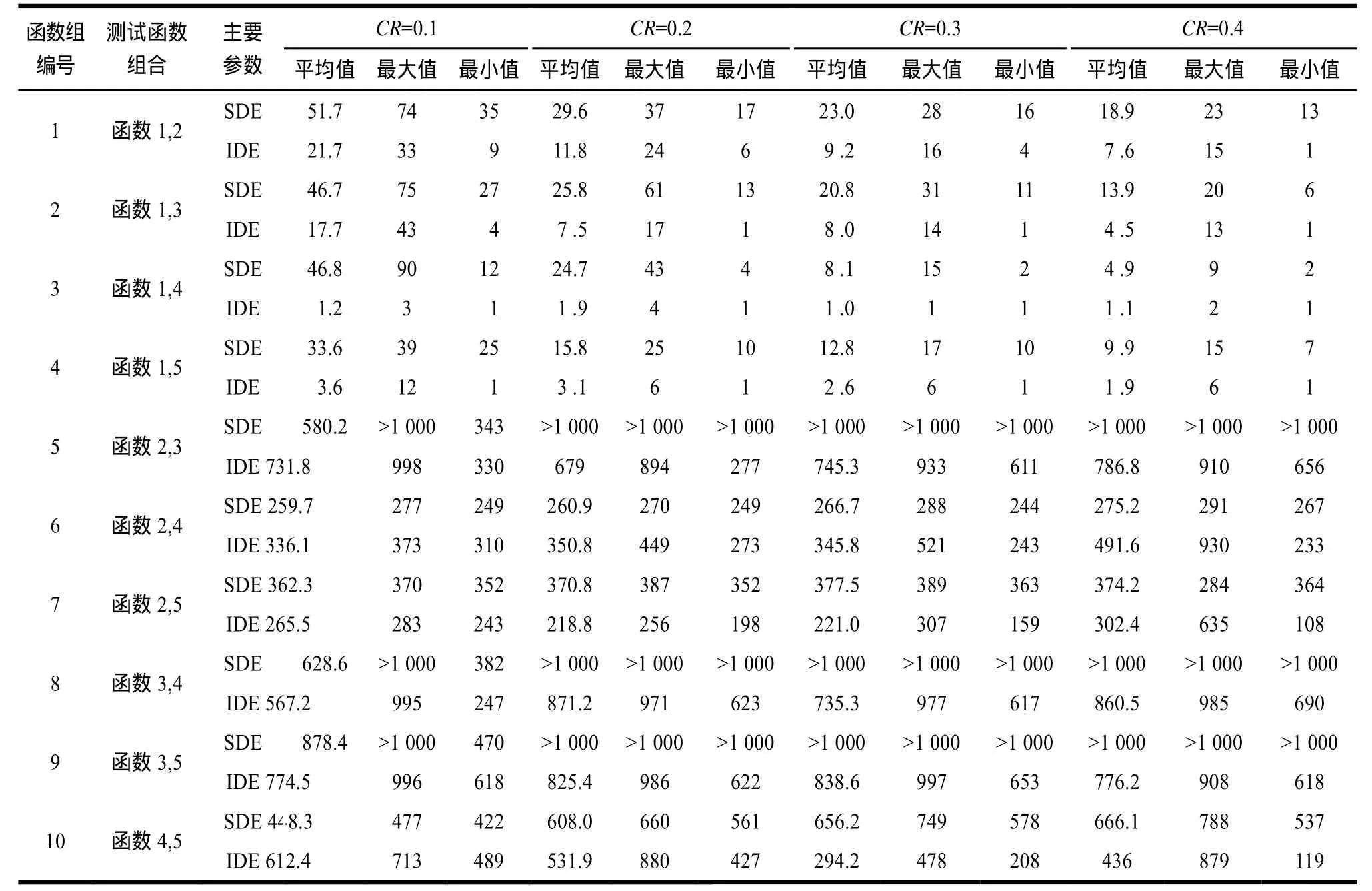
表3 高维条件下(2,10,5,10,5)5个基本函数组合改进前后的迭代步骤数比较

如表2所示，在低维条件下，本文改进的多目标差分进化算法和标准多目标差分进化算法都可以在较短的迭代步骤数中达到多目标问题的达标值。如表3所示，在高维条件下，标准多目标差分进化算法在部分情况下(如函数3、函数5)，在1 000步内已经很难达到达标值时，本文的差分进化算法依然可以在1 0 00步的迭代步骤数中使种群满足达标的最优值。

图1、图2展示了标准多目标差分进化算法和本文差分进化算法在不同的函数组合条件下迭代结束时，标准的多目标差分进化算法与本文中改进的多目标差分进化算法的平均最优值乘积的比较。

图1 低维条件下不同目标函数组合与函数平均乘积最优值关系

图2 高维条件下不同目标函数组合与函数平均乘积最优值关系

图1展示了在低维环境下，改进的多目标差分进化算法的平均最优值乘积优于标准多目标差分进化算法。图2展示了在高维环境下，改进的多目标差分进化算法的平均最优值乘积也优于标准多目标差分进化算法，2种多目标差分进化算法之间差值变大，且标准多目标差分进化算法不能找到最优值的目标函数组也变多。

图3、图4分别展示了标准多目标差分进化算法和本文差分进化算法，在不同的函数组合条件下迭代结束时，在不同交叉概率的情况下，标准多目标差分进化算法与本文改进的多目标差分进化算法的函数平均最优值乘积的比较。

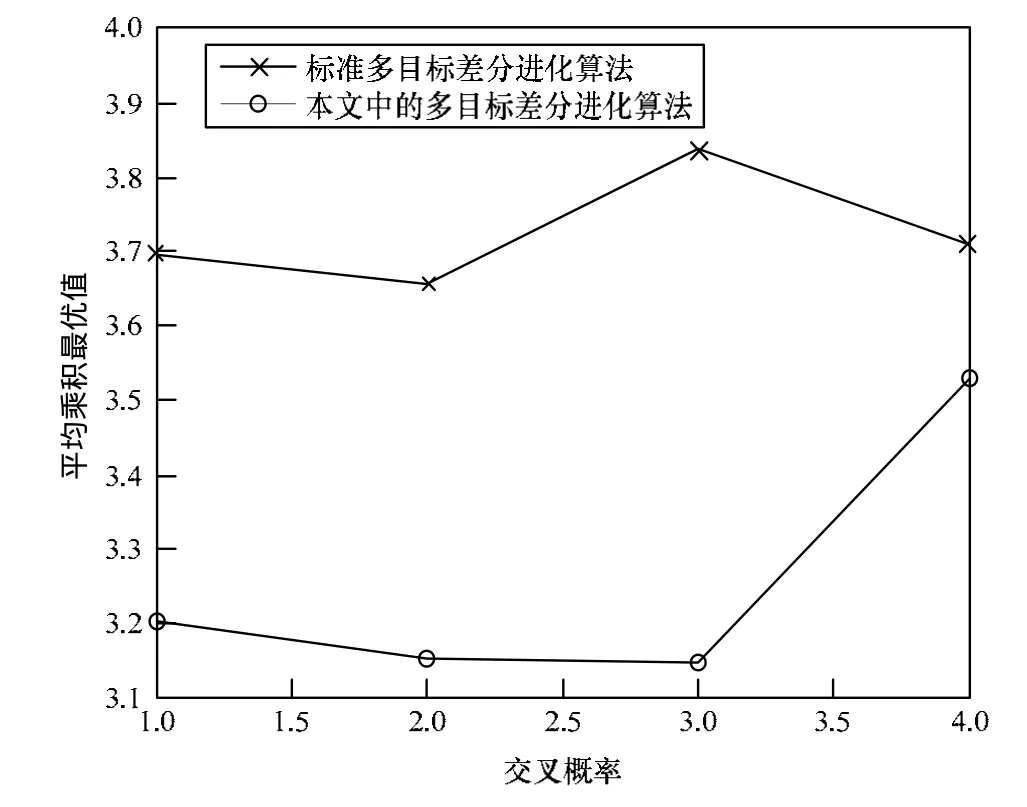
图3 低维环境下不同交叉概率与函数平均乘积最优值的关系

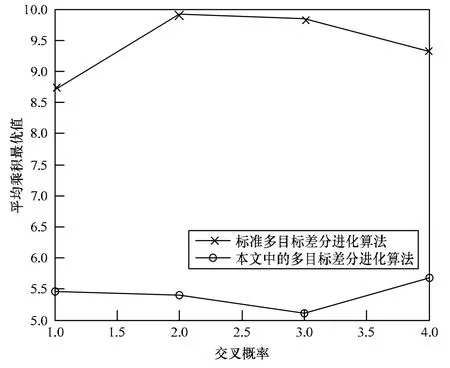
图4 高维环境下不同交叉概率与函数平均乘积最优值的关系

图3展示了在低维条件下，不同交叉概率下改进的多目标差分进化算法相较于标准差分进化算法可以找到更优的函数平均最优值乘积。图4展示了在高维条件下，改进的多目标差分进化算法依然可以找到比标准多目标差分进化算法更优的函数平均最优值乘积，且2种多目标差分进化算法之间的差值变大，在部分情况下，如交叉概率为0.3时，2种多目标差分进化算法之间的差值甚至达到1倍左右。

图5、图6展示了在低、高维条件下平均最优值乘积与迭代步骤数之间的关系。其中，在图中展示的迭代步骤数为100步。在如图5所示的低维条件下，2个函数都可以在较短的迭代步骤数 内找到平均最优值乘积，且在相同迭代步骤数下，改进的多目标差分进化算法可以找到更好的平均最优值乘积。在如图6所示的高维条件下，改进的多目标差分进化算法依然可以在相同迭代步骤数下，找到更好的函数平均最优值乘积，并且2种多目标差分进化算法之间的差值变大。

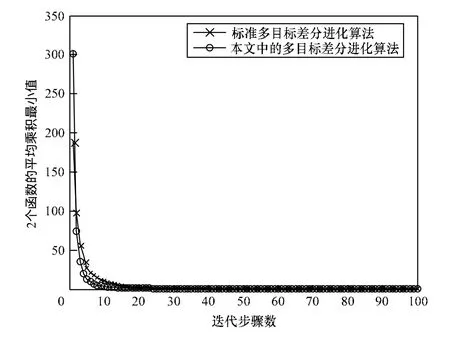
图5 低维环境下迭代步骤数与平均乘积最优值之间的关系

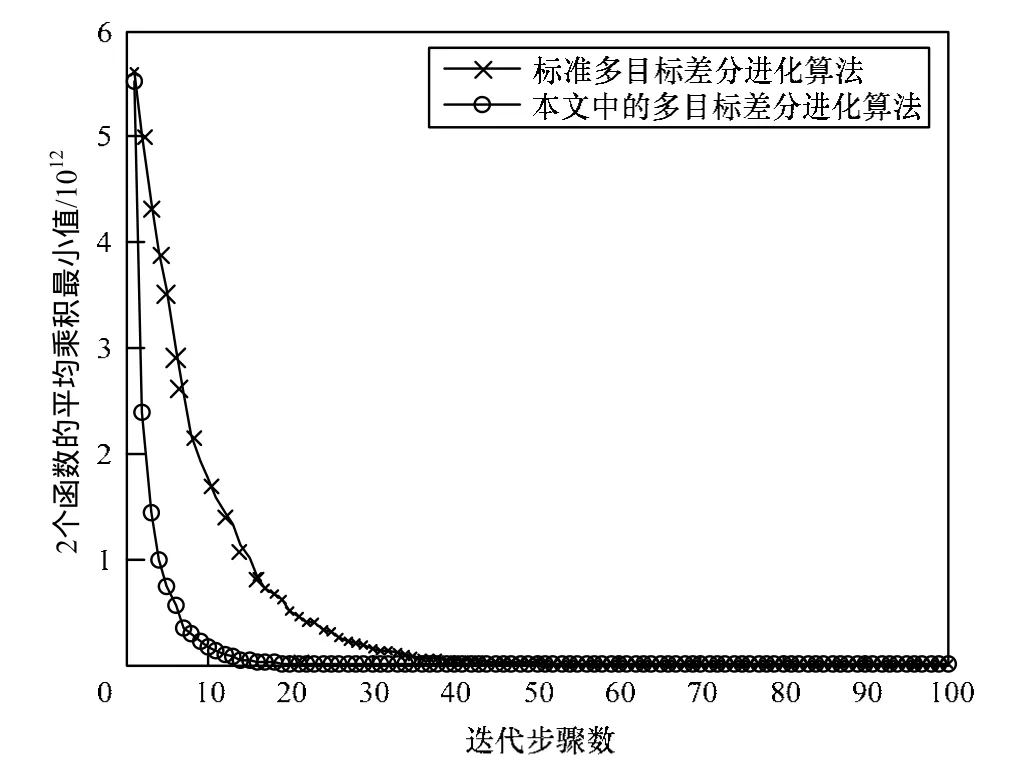
图6 高维环境下迭代步骤数与平均乘积最优值之间的关系

5 结束语

本文通过引入多个不同变异个体和在交叉操作中引入多个交叉概率，提出基于多个变异个体的改进的多目标差分进化算法。通过理论推导及实验，证明改进的多目标差分进化算法较标准多目标差分进化算法在相同迭代步骤下，可以找到更好的最优值解。由于本文中的实验有限，仅测试了2个目标函数组的情况，对于本文中改进的多目标差分进化算法是否可以在多个目标函数的情况下，依然保持其良好的性能，以及本文中改进的基于多变异个体的多目标差分进化算法与其他的多目标优化算法的优缺点的比较，则需要进一步理论论证以及实验证明。

[1] S torn R, Price K. Differential Evolution——A S imple and Efficient He uristic f or Gl obal Optimization o ver Continuous Spaces[J]. Journal of Global Optimization, 1997, 11(1): 341-359.

[2] S torn R, Price K. Minimizing the Real Functions of the ICEC’96 Contest by Differential Evolution[C]//Proceedings of IEEE Conference on Evolutionary Computation. [S. 1.]: IEEE Press, 1996: 231-236.

[3] Chakraborty U K, Das S, Ko nar A. Dif ferential Evolution with Local Ne ighborhood[C]//Proceedings of IEEE Con ference on Evolutionary Co mputation. [S. 1.]: IEEE P ress, 2 006: 20 42-2049.

[4] 邵 梁. 基于排序采样策略的差分演化算法[J]. 计算机工程与应用, 2012, 48(1): 49-52.

[5] 邓泽喜, 曹敦虔, 刘晓冀, 等. 一种新的差分进化算法[J].计算机工程与应用, 2008, 44(24): 40-42.

[6] 雍龙泉, 陈 涛, 张建科. 求解互补问题的极大熵差分进化算法[J]. 计算机应用研究, 2010, 27(4): 1308-1310.

[7] 杨启文, 蔡 亮, 薛云灿. 差分进化算法综述[J]. 模式识别与人工智能, 2008, 21(4): 506-513.

[8] 刘 波, 王 凌, 金以慧. 差分进化算法的研究进展[J].控制与决策, 2007, 22(7): 721-729.

[9] 王筱珍, 李 鹏, 俞国燕. 分阶段二次变异的多目标混沌差分进化算法[J]. 控制与决策, 2011, 26(3): 457-163.

[10] 牛大鹏, 王福利, 何大阔. 多目标混沌差分进化算法[J].控制与决策, 2009, 24(3): 261-264.

[11] 孟红云, 张小华, 刘三阳. 用于约束多目标优化问题的双群体差分进化算法[J]. 计算机学报, 2008, 31(2): 228-235.

[12] Zitzler E, Thiele L. Multiobjective Evolutionary Algorithms: A Comparative Case Study and the Strength Pareto Approach[J]. IEEE Transactions on E volutionary Computation, 1999, 3(4): 257-271.

[13] Madavan N K. Multiobj ective Optimization U sing a Pareto Differential Evolution Approach[C]//Proceedings of IEEE Conference on E volutionary Computation. Piscataway, USA: IEEE Press, 2002: 1145-1150.

[14] R obic T, Filipic B. DEMO: D ifferential Evolution for Multi-objective Optimization[C]//Proceedings of EM O’05. Berlin, Germany: Springer, 2005: 520-533.

[15] 公茂果, 焦李成, 杨咚咚, 等. 进化多目标优化算法研究[J].软件学报, 2009, 20(2): 272-289.

[16] 谢 涛, 陈火旺, 康立山. 多目标优化的演化算法[J]. 计算机学报, 2003, 26(8): 997-1003.

[17] 周育人, 闵华清, 许孝元, 等. 多目标演化算法的收敛性研究[J]. 计算机学报, 2004, 27(10): 1415-1421.

编辑 索书志

Improved Multi-objective Differential Evolution Algorithm Based on Multi-mutation Individuals

SHEN Jia-jie, JIANG Hong, WANG Su

(School of Information Science Technology, East China Normal University, Shanghai 200241, China)

Aiming to the problem of multi-objective Differential Evolution(DE) algorithms which have the characteristics of prematurity and slow convergence speed under high-dimensional situation, this paper prop oses an improved mul ti-objective DE algorithms based on multi-mutation samples. Through using method of introducing multi-mutation individuals into the mutation operator and crossover operator of multi-objective DE algorithm, multi-objective DE algorithm popu lations can keep diversity, reduce the possibility of falling into local optimal solution, it has guick speed for optimal solution, and the improves the ab ility finding optimal solution using shorter iteration steps than standard multi-objective differential evolution algorithm. Experimental results show that compared with standarded multi-objective DE algorithms, the improved algorithm can find optimal value effectively in high-dimensional multi-objective environment.

multi-objective optimizat ion problem; D ifferential Evolution(DE) algorithm; multi-mutation individuals; computational intelligence; optimal value searching; iteration speed

10.3969/j.issn.1000-3428.2014.05.042

国家“863”计划基金资助项目(2013AA01A211)。

沈佳杰(1989－)，男，硕士研究生，主研方向：多目标优化；江 红，副教授；王 肃，讲师。

2013-05-07

2013-06-03E-mail：51111211010@ecnu.cn

1000-3428(2014)05-0203-06

A

TP18