基于约束规划的岸桥与集卡集成调度

秦天保，彭嘉瑶，沙 梅

(上海海事大学交通运输学院，上海 200135)

基于约束规划的岸桥与集卡集成调度

秦天保，彭嘉瑶，沙 梅

(上海海事大学交通运输学院，上海 200135)

针对进口集装箱卸船的岸桥与集卡集成调度问题，分别提出混合整数规划(MIP)模型和约束规划(CP)模型，目标是使得卸船完工时间最短，该问题是NP难题。通过OPL语言设计约束规划模型，利用其为调度问题提供的特殊构造，如区间变量、序列变量等进行建模，并采用“扩展操作任务”的概念来定义区间变量以提升求解效率。为评价解的质量，设计一个新的下界求解方法。使用不同规模的实例对约束规划模型和MIP模型进行测试，结果表明，在小规模实例中，CP模型求解性能略差于MIP模型，但对于中大规模实例，MIP模型无法在设定时限内找到解，而CP模型则能以较快的收敛速度得到高质量的解，目标距离下界的差距控制在2.19%～8.28%。

岸桥调度；集卡调度；约束规划；集装箱码头；最优化；启发式算法；混合整数规划

1 概述

岸桥调度问题(Quay Crane Scheduling Problem, QCSP)和码头堆场内部集卡调度问题(Yard Truck Scheduling Problem, YTSP)是集装箱码头作业系统2个重要的子问题，指为岸桥和集卡制定工作计划，使得某个目标最优(通常为完工时间最短)。

现有文献大多分开研究这2个子问题。针对岸桥调度问题，文献[1]建立了混合线性整数规划(Mixed Integer Linear Programming, MILP)模型，并提出分支定界算法(B&B)求解；文献[2]设计了一种禁忌搜索算法求解该问题；文献[3]将随机贪婪适应性搜索算法融入遗传算法求解岸桥调度；文献[4]提出了带时间窗的岸桥调度混合整数规划(Mixed Integer Programming, MIP)模型，并设计了遗传算法求解。针对集卡调度问题，文献[5]提出了贪婪算法研究集卡调派问题；文献[6]设计了遗传算法求解集卡调度问题；文献[7]对集装箱码头集卡分配问题建立了整数规划模型；文献[8]设计了现代集装箱码头集卡调度系统，提出了集装箱码头物流系统有色Petri网建模的基本构架和一种新的遗传算法调度编码方式。文献[9]针对集卡调度，提出了基于能力约束判断的资源协作模型，并设计了改进的量子遗传算法进行求解。文献[10]提出一种面向整个码头作业面的动态蚁群算法来动态优化集卡调度路径。

由于岸桥和集卡具有很强的交互作用，将两者进行集成调度能够得到更好的全局解，这就是岸桥与集卡集成调度问题(Integrated Quay Crane and Yard Truck Schedule Problem, IQCYTSP)。但集成调度文献较少，文献[11]研究了该问题，但该文实际上是基于时间最短的集卡线路优化模型，对岸桥的处理仅使用了其作业时间，将所有岸桥作为一个整体考虑，没有涉及到岸桥和集卡之间作业时间衔接的约束以及岸桥执行各个任务的调度。文献[12]研究了集卡与岸桥联合调度问题，建立了混合整数规划MIP模型，并设计了遗传算法和修订的基于约翰逊规则的启发式算法求解，但其只求了小规模的问题。

IQCYTSP问题是NP难题[12]，现有研究基本上都是设计各种启发式算法进行求解。本文建立一个新的规范化MIP模型和一个约束规划(Constraint Programming, CP)模型，设计新的下界，对该问题进行实验求解。一方面，通过实验判断约束规划技术应用于本问题的适用性；另一方面，为学术界求解此类问题提供一个新的思路。

2 问题描述与MIP模型

集装箱码头船舶装卸有多种组织模式，本文研究一种较常见的组织方式，即作业线方式。一组岸桥服务于一艘船，卸船先于装船，本文只考虑卸船过程。船上的集装箱依贝号划分为若干区域，在一般情况下，每个区域配备一台岸桥，在每台岸桥要卸载的集装箱区域已知的情况下，只需考虑单台岸桥的调度，所有岸桥调度结果是单台岸桥调度结果的简单综合。一组固定的集卡服务一台岸桥，称为一条作业线。集卡在岸桥处接受岸桥卸下的箱子，运输到堆场指定箱区，由堆场场桥卸下箱子，集卡再空载返回到岸桥下接受下一个箱子。船上的箱子被岸桥卸载的时间不同，通常，靠近岸边的箱子比远离岸边的箱子卸载时间短，上面的箱子比下面的箱子卸载时间短；另外，码头实践中，船上的箱子已事先根据计划指定了其在堆场的卸载位置，因此集卡运输不同箱子到堆场的时间不同，这样，不同的集装箱卸载次序和对集卡的不同任务分配会导致不同的完工时间，该问题需要寻求一个最优的卸载次序以及集卡任务分配以使得总完工时间最短。

该问题还有一个特点，即岸桥从船上卸载一个箱子后，若下面无集卡(集卡可能还未返回)，则岸桥必须等待，即处于阻塞状态，这一点模型中必须考虑，为此，设计2个决策变量，为岸桥从船上提箱i并移动到陆侧的时间，本文称之为岸桥卸载箱子i的结束时间，di为岸桥放下箱子i到集卡的时间，也就是箱子离开岸桥的时间，即为岸桥阻塞的时间。岸桥放下箱子到集卡上后才能开始一段过渡时间去卸下一个箱子。下面首先提出一个针对此问题的MIP模型。

2.1 模型参数

MIP模型各参数如下：

n：箱子数目；

m：集卡数目；

pi：岸桥卸载箱子i需要的时间

ti：集卡运输箱子i到堆场的时间，也等于其返程时间

d：场桥从集卡卸载一个集装箱到堆场所需时间；

sij：岸桥放下箱子i到集卡上后，立即卸载箱子j的过渡时间

M：一个足够大的正数。

2.2 决策变量

决策变量如下：

Cmax：所有任务完成的时间，即所有集装箱经过岸桥卸船、集卡运输、场桥卸载到堆场的结束时间；

di：岸桥卸下箱子i并放到集卡上的时间点，即箱子离开岸桥的时间

xik：如果箱子i分配给集卡k运输，取1，其他取0

yij：如果箱子i在箱子j之前卸载或运输，取1，其他取

2.3 MIP模型

MIP模型描述如下：

目标函数式(1)是最小化所有箱子由船舶卸载到堆场存放的完工时间；约束式(2)定义总完工时间，要求其大于所有箱子运到堆场并堆放完成的时间；约束式(3)保证岸桥卸载箱子i的结束时间大于卸载时间(不包含岸桥等待集卡的时间)；约束式(4)保证任一箱子只能分配给一辆集卡运输；约束式(5)保证箱子i离开岸桥的时间大于岸桥卸载箱子i的结束时间；约束式(6)保证箱子i离开岸桥的时间等于集卡开始运输i的时间，该约束表达了岸桥和集卡间的衔接关系；约束式(7)和式(8)保证岸桥卸载2个不同箱子间要经过一段过渡时间；约束式(7)表示如果箱子j先于i被岸桥卸载(yij=0)，则j离开岸桥后至少经过sji的过渡时间才能开始卸载i；约束式(8)表示如果箱子i先于j被岸桥卸载(yij=1)，则i离开岸桥后至少经过sij的过渡时间才能开始卸载j；约束式(9)和式(10)保证分配给同一集卡的2个箱子运输任务间至少要经过一段过渡时间；约束式(9)表示若箱子j先于i被同一集卡k运输(yij=0，xik、xjk=1)，则j运输并堆放到堆场完成后，至少经过tj的过渡时间(即返程时间)才能开始运输i；约束式(10)表示若箱子i先于j被同一集卡k运输(yij=1，xik、xjk=1)，则i运输并堆放到堆场完成后，至少经过ti的过渡时间(即返程时间)才能开始运输j；式(11)和式(12)是决策变量域约束。

由于该问题是NP难题[10]，对大规模问题，MIP模型会难于求解(下文第4节的实验也验证了这一点)，为此，本文在第3节提出针对此问题的一个CP模型，并测试和评价其求解效率。

3 约束规划模型

3.1 模型特点

下面建立相应的CP模型。CP模型在不同CP系统中表示方法不同，其表达方式也未达成一致。本文所建CP模型是用IBM ILOG CPLEX Optimization 12.4中的OPL 12.4语言实现的。OPL针对调度问题提出了一种新的概念，即区间(决策)变量，区间变量概念是对约束规划在调度领域应用的一个重要扩展。文献[13]介绍了约束规划中应用区间变量的内在机制。区间变量不同于一般MIP模型中的决策变量，区间变量具有起点、终点和长度(通常情况下，区间变量的长度等于终点-起点)等内在属性，起点、终点都是整数，故以下的约束规划模型中，时间都被离散化为整数。

区间变量经常用于建模一段任务(活动)时间，起点为任务开始时间，终点为任务结束时间。本文提出的CP模型就是基于区间变量设计的。约束规划系统提供大量函数访问区间变量的属性和设置约束。为简单起见，主要采用文献[13] 和OPL中的符号表示法来表示基于区间变量的约束规划模型，该文献中提出的“活动”变量就是区间变量的雏形，其提出的许多作用于活动变量的函数亦可用于区间变量，这些函数都是简单自明的，如start(a)表示区间变量a的起点，end(a)表示区间变量a的终点，presence(a)表示区间变量a是否出现在最终调度中(即在最终调度中是否被执行)。文中采用的一些函数和构造若文献[14]中没有，则直接采用OPL中的构造，这些函数和构造将在下面模型中出现时再解释。采用这套表示法表达的约束规划模型很容易转化成OPL语言实现。

本文建立的CP模型有一个特色，就是对区间变量所代表的操作任务有不同的定义。传统上，一个操作任务就是设备完成一个集装箱操作所需的时间，它不包含设备阻塞的时间（比如岸桥卸箱时等待集卡的时间），本文把这样定义的操作任务称为“基本操作任务”，在前面的MIP模型中，对操作任务即采用此定义。

本文建立过一个将区间变量定义为基本操作任务的CP模型，通过实验发现求解效率不够高。为此，笔者引入了一个新的任务定义，即在CP模型中，将设备操作任务定义为包含阻塞时间的操作任务，将包含阻塞时间的操作任务称为“扩展操作任务”。例如，岸桥卸载箱子的扩展操作任务包含岸桥吊具从岸边移到船上提箱，送到岸边，再加上等待集卡的时间。笔者发现，将区间变量定义为扩展操作任务所建立的CP模型，求解效率会提高很多，因此，以下CP模型中区间变量即采用扩展操作任务的定义。

3.2 模型参数

3.3 决策变量与约束条件

3.3.1 区间决策变量

本CP模型定义了3组区间决策变量：qtasksi, ytasksi和ytTaskski。qtasksi表示岸桥卸载箱子i的扩展任务，其域为[0, H]。其起点表示任务开始时间，终点表示任务结束时间，长度即为卸载该箱子的持续时间（包含阻塞时间）。

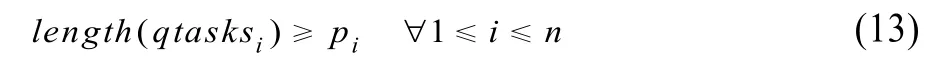
约束式(13)规定岸桥的集装箱操作任务(扩展操作任务)时间长度不小于相应的基本操作任务时间pi，因为如前所述，CP模型中的定义的任务时间包含阻塞时间，所以长于实际的操作时间。

区间变量ytasksi表示集卡运输箱子i的任务(注：这里将运输任务执行时长定义为集卡运输时间加上场桥卸载时间)，其域为[0, H]。以下给出对该区间变量ytasksi的限制约束：

二维区间变量ytTaskski表示集卡k运输箱子i的任务，定义为可选(optional)区间变量，其域为[0, H]。它表示一个运输任务可能由任意一个集卡完成，最终会利用选择约束约束)来限制仅能由一辆集卡完成。因此，可以将ytTaskski理解为一种模式选择区间变量，即一个任务可能有多种完成模式(一辆集卡为一个模式)。要间隔一段过渡时间。为实现这个约束，首先定义一个过渡函数：

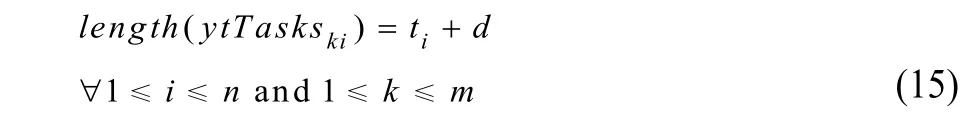
ytTaskski定义为OPL可选变量，说明并非所有ytTaskski都必须执行，只有那些被选中的才会被执行。

3.3.2 集卡任务分配

ytasksi和ytTaskski受限制于选择(alternative)约束式(16)，表示如果运输任务ytasksi执行，则所有的ytTaskski(k=1, 2,…, m)中只能有一个执行(其他不执行，也就是其present状态为0)，且其起止时间与ytasksi完全相同，这样就能保证每个箱子只能由一辆集卡来运输，即将任务分配给特定的集卡。

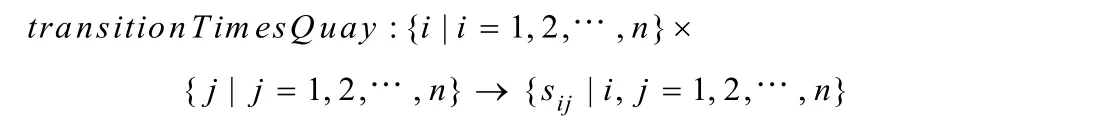
该函数用于定义岸桥卸载任务(箱子)i到j的过渡时间为sij。然后定义一个序列变量qsequence：

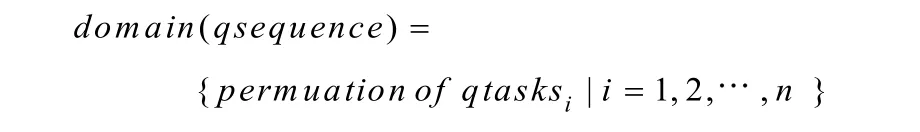
为序列变量中的任务分配类型：

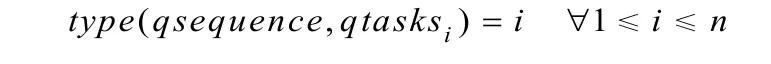
任务类型就是任务(箱子)编号。利用noOverlap(不重叠)约束式(18)来保证该序列中的任务不能重叠，且2个相继任务之间需要一段过渡时间。

3.3.4 无缓冲约束

在卸船的过程中，对任一箱子i，岸桥卸载的扩展操作任务结束时间要等于集卡运输的开始时间，2个阶段间没有缓冲区。约束式(19)表达了岸桥和集卡间这种无缓冲的衔接关系。

3.3.3 任务排序约束

每一个集卡k执行自己的运输任务ytTaskski(i=1,2,…,n)互相不能重叠，即集卡只能一次一个依次运输箱子，因此，需要确定任务在集卡上执行的排序。集卡卸箱到堆场后，需要一段返程时间回到岸桥，才能开始下一个运输任务，故集卡的2个相继运输任务之间有过渡时间，这个过渡时间就是返程时间，本文假设集卡运输集装箱i的返程时间也是ti。OPL提供了序列变量这一新型决策变量来高效建模排序约束。首先，定义过渡函数：

3.3.5 资源消耗限制约束

以上约束已经可以完全描述本文的问题，但为进一步提高CP引擎的求解效率，引入累积约束式(20)，它可以表示任一时刻所有任务消耗的资源总数不得超过设定值。本文将集卡作为资源，任何一个集卡任务ytasksi执行期间会消耗一辆集卡资源，任一时刻，集卡总消耗量不得大于集卡总数m。由于累积约束是全局约束，因此非常有助于求解器进行全局推理，从而提升求解效率。

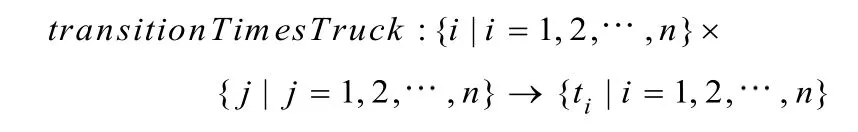
该函数定义了集卡任务i到j的过渡时间为ti(如果返程时间不是ti，则修改过渡函数中的参数ti为实际返程时间即可)。在集卡k执行的任务集合上定义序列变量ysequencek，其域为：

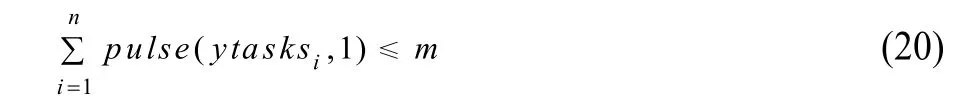
其中，pulse函数是OPL中的基本累积函数，其第1个参数表示消耗资源的区间变量，第2个参数表示区间变量在其执行过程中消耗的资源数(集卡数)。基本累积函数求和后成为汇总累积函数，它代表了所有基本累积函数执行过程中消耗的资源总量，对汇总累积函数施加约束即为资源约束，这里运输任务消耗的集卡数不超过集卡总数。

图1表示了汇总累积函数消耗资源的曲线，其中，H表示资源量限制，各个a是区间变量。可以看出，每个区间变量执行时，使得汇总累积函数曲线增加，区间变量执行完后，使得汇总累积函数减少。对汇总累积函数上限施加的限制就是累积约束，也就是资源限制约束。

可见序列变量可能的取值为一组区间变量的所有排序。可以对序列变量中各个任务分配一个类型，如：

图1 汇总累积函数

类似地，所有的岸桥任务qtasksi也互相不能重叠，即岸桥只能一次一个依次卸载箱子，因此，需要确定任务在岸桥上执行的排序，而且岸桥执行2个相继任务之间还需

3.4 目标函数

目标函数式(21)是最小化最晚完工的集卡任务的完工时间，即整体完工时间。

通过比较CP模型和MILP模型，可以发现CP模型约束表达自然简洁，由于可以自然地表达逻辑约束，无需使用大量0-1变量。

3.5 搜索策略

为进一步提升ILOG CP优化器搜索本问题解空间的搜索效率，可以对其默认搜索策略进行调整，搜索策略包含多方面的内容，这里要调整的是搜索变量的次序，和为变量赋值的次序(例如从小到大还是从大到小赋值)，研究发现，这些次序有时会极大地影响搜索效率。本文利用ILOG CP提供的搜索阶段机制来干预其搜索策略。通过搜索阶段可以指定CP优化器搜索时固定变量的次序，笔者通过实验尝试了不同的次序，发现先固定序列变量ysequence，再固定qsequence的搜索效率最高(变量赋值的次序采用系统默认次序)。搜索阶段用ILOG脚本定义如下：cp.setSearch Phases (f.searchPhase(ysequence), f.searchPhase(qsequence))。

4 下界分析

下文分别对LB1和LB2进行分析。

4.1 LB1分析

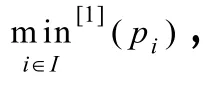
以此类推，首次行程中最后一辆集卡的出发时间下界LB1为：

4.2 LB2分析

令T1为运完所有集装箱需要的所有集卡总运输时间，这个时间包括集卡堆场卸载和返程时间，但不包括集卡在岸桥下等待的时间，并且假设包含各集卡最后一次运输的返程时间，则有：

令T2为最后一辆集卡首次行程出发前其他集卡已完成的总运输时间上界，T3为各集卡最后一次运输所对应的总返程时间上界(由于是最后一次运输，因此实际上无需返程)，则有：

为了评价CP模型的求解质量，需要得到较紧的下界，本节提出一个新的求解上述问题下界的方法。为了定义该下界，本文首先定义2个要用于下界计算的算符。

定义定义min[k]为取一列数值中第k小的数，max[k]为取一列数值中第k大的数。

例如，给定一列数值S={10, 3, 6, 6, 7, 9 }，则：

也就是说首次行程中最后一辆集卡出发后剩下的集装箱需要的总运输时间(包括集卡堆场卸载时间和返程时间)的下界LB2等于所有集装箱需要的总运输时间T1减去该集卡出发前其他集卡已完成的总运输时间上界(因为这些时间已被用掉)T2，再减去各集卡最后一次运输所对应的总返程时间上界(因为最后一次无需返程)T3。

为计算T2，考虑首次行程中共有m个箱子需要卸载。在最后一辆集卡出发前，第1辆集卡消耗的运输时间为岸桥卸载后m–1个箱子的时间及必要的过渡时间，这个时间的上界为：

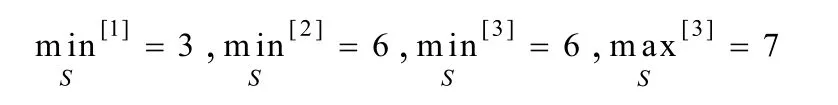
注意，将这列数值先排序后会更加容易看出算符的操作结果，另外，允许这一列数值中有重复的数。

定理假设有m辆集卡运输m个集装箱，1台岸桥，则该IQYSP问题的下界LB可由下式求得：

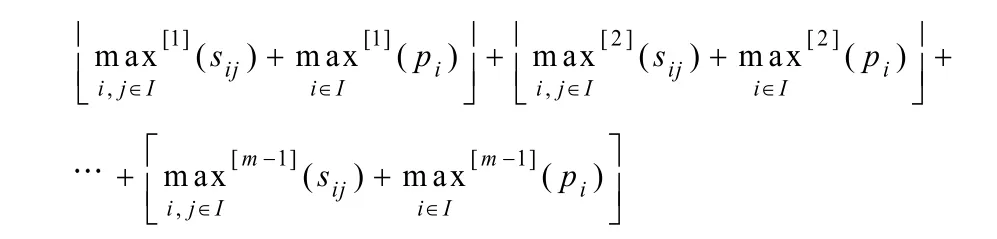
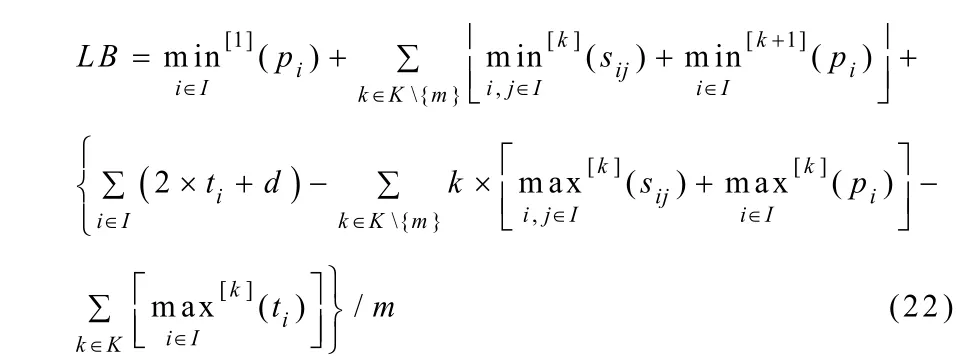
证明：令LB1为首次行程中最后一辆集卡的出发时间的下界。首次行程指各集卡第一次运输箱子的行程，最后一辆集卡的出发时间即一开始排在最后的那辆集卡接受岸桥卸下箱子开始运输的时间。令LB2为首次行程中最后一辆集卡出发后剩下的集装箱需要的总运输时间(包括集卡堆场卸载时间和返程时间，但不包括集卡在岸桥下等待的时间)下界。则容易看出，下式成立：

同理，第2辆集卡消耗的运输时间为岸桥卸载后m–2个箱子的时间及必要的过渡时间，这个时间的上界为：

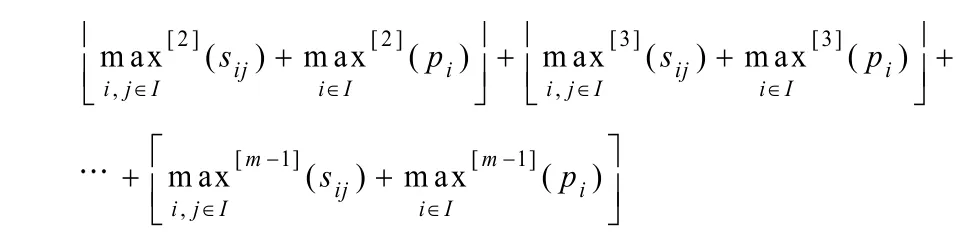
以此类推，可求得首次行程中前m–1辆集卡消耗的运输时间上界，把它们相加，即得到T2：

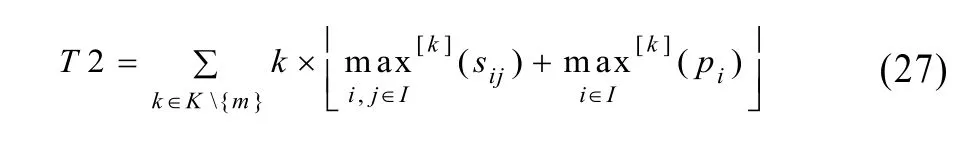
T3比较简单，可由下式得到：

将式(25)、式(27)、式(28)中的T1，T2，T3代入式(26)，再将式(26)和式(24)代入式(23)，即可得到式(22)，定理得证。

5 数值实验

本节报告数值实验结果，将以上约束规划模型用IBM ILOG CPLEX Optimization Studio 12.6中的OPL语言实现，并利用其中的CP优化器求解。计算时将系统参数Sequence InferenceLevel和NoOverlapInferenceLevel都设为5，Workers参数设为1。测试硬件平台为4核Intel Xeon E3 3.7 GHz CPU，8 GB内存。

为了测试CP方法能否求解实际规模的实例，随机生成了7个不同规模的实例集，每个实例集含5个实例。各实例集集装箱数(即任务数)分别为10，20，30，40，60，80，100，集卡统一为5辆。生成数据时设置pi服从[45, 85]上的均匀分布，ti服从[180, 600]上的均匀分布，sij服从[20, 40]上的均匀分布，d为50。

5.1 小规模实例测试

对于10个任务5辆集卡的小规模实例，利用数学规划求解软件Gurobi 5.01求MIP模型，可得最优解，本文比较了64位的Gurobi得到的最优目标值和CP的求解结果(CP求解时限设为5 min)，见表1。其中，“Gurobi”列是Gurobi求得的最优目标值和求解时间；“CP”列是CP模型1 min内求得的最佳目标值和求得该值的时间；“差距”列是CP目标值相对最优目标的百分比差距。可以看见，CP方法在2 s以内全部求到最优解，说明CP的求解效率和求解质量都很高。

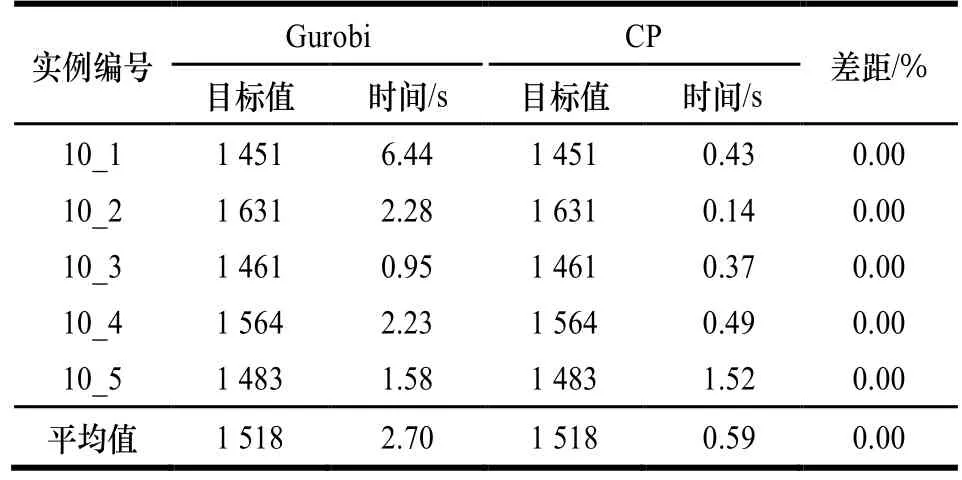
表1 小规模实例结果比较

5.2 中大规模实例测试

本节进一步测试CP方法对中大规模实例的求解结果，求解时限为半小时(Gurobi无法在半小时时限内求解这些实例)。为更准确地观察求解收敛情况与解的质量，本文分3个时间段统计了实验结果，分别设定为1 min、2 min、5 min，表2统计了6个实例集(每个实例集含5个实例)的平均计算结果，其中，“下界”列表示每个实例集中5个实例的平均下界；“目标”列是CP在相应时段内求得的每个实例集中5个实例的最佳目标值的平均值；“时间”列是求得实例集中各实例最佳目标的时间的平均值；“差距”列是实例集中各实例最佳目标相对下界的百分比差距的平均值。可以看出，CP求解的收敛速度很快，在1 min内就能得到较好的解，各实例集求解的平均目标距离下界的差距在5%以内，这种快速收敛的特性非常有利于码头实时调度。

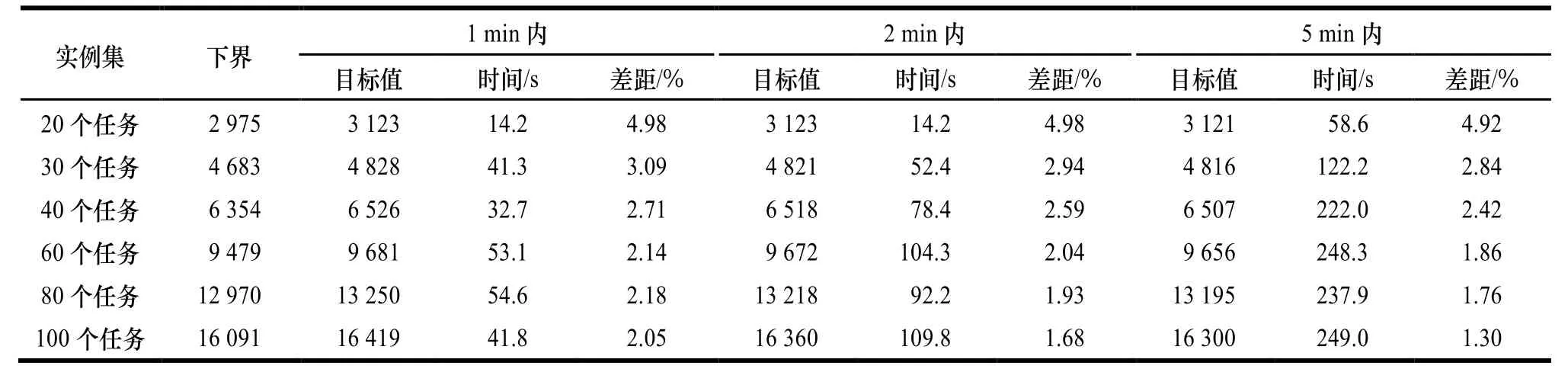
表2 中大规模实例测试结果

图2展示了一个100个任务的实例(实例100_1)求解收敛过程，可以看出早期收敛是非常快的，在最初1 min内就收敛到下界附近了。

以上测试考察了集装箱数量对装卸时间的影响，为考察集卡数量对装卸时间和求解性能的的影响，本文对100个任务的实例集分别测试5辆、8辆和10辆集卡的情况，求解时限设为5 min，在5 min内求得的最佳目标值(完工时间)见表3。可以看出，集卡数目对目标值影响很大，集卡从5辆增加到10辆，装卸完工时间平均可减少40%以上(假设场桥总是可用)。

图2 100个任务的实例求解收敛过程

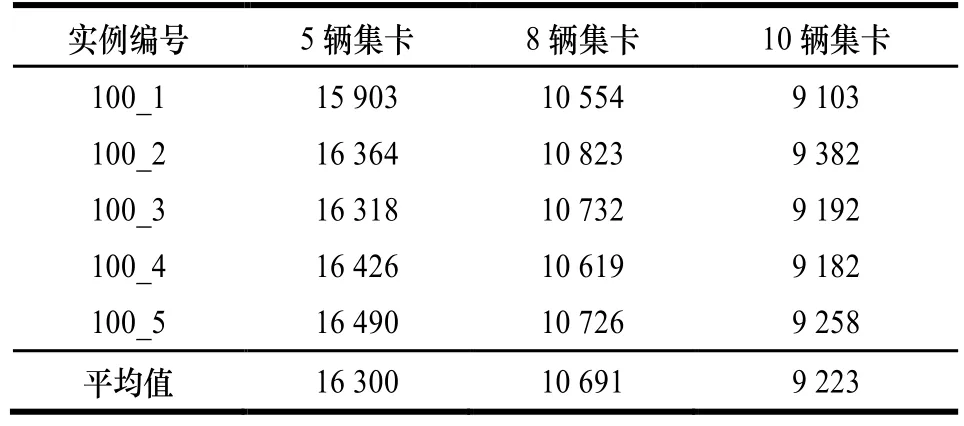
表3 不同集卡数量时的测试结果

6 结束语

本文采用CP技术建模求解岸桥与集卡联合调度问题，在采用了提高求解效率的累积约束以及更高效的约束表达式后，利用不同规模实例进行测试，实验结果显示CP具有很高的求解效率和求解质量，能够求解规模更大的问题。CP的另一个重要优势是可以采用高级建模语言以声明性语法(本文采用OPL语言)建模，这使得模型清晰易懂，便于根据实际情况随时修订约束。而其他文献多采用启发式算法求解问题，由于没有清晰的模型表达机制，使得修改约束较为麻烦。CP技术兼具灵活性和效率的特点使其成为求解码头运营问题的有效工具。未来可考虑扩展模型，将场桥调度也集成进来，形成岸桥、集卡和场桥集成调度模型。

[1] Kim K H, Park Y M. A Crane Scheduling Method for Port Container Terminals[J]. European Journal of Operational Research, 2004, 156(3): 752-768.

[2] Sammarra M, Cordeau J F, Laporte G, et al. A Tabu Search Heuristic for the Quay Crane Scheduling Problem[J]. Journal of Scheduling, 2007, 10(4/5): 327-336.

[3] 曾庆成, 高 宇. 集装箱码头装卸桥调度优化模型与算法[J]. 计算机工程与应用, 2006, 42(32): 217-219.

[4] 董良才, 丁以中, 宓为建. 基于时间窗的集装箱装卸桥调度[J]. 上海海事大学学报, 2011, 32(1): 1-7.

[5] Bish E K, Chen F Y, Leong Y T, et al. Dispatching Vehicles in a Mega Container Terminal[J]. OR Spectrum, 2005, 27(4): 491-506.

[6] Ng W C, Mak K L, Zhang Y X. Scheduling Trucks in Container Terminals Using a Genetic Algorithm[J]. Engineering Optimization, 2007, 39(1): 33-47.

[7] 吕显强. 集装箱码头分派车辆的整数规划模型[J]. 大连水产学院学报, 2004, 19(6): 18-20.

[8] 康志敏, 吴洪明. 港口集装箱码头集卡优化调度研究[J].物流工程与管理, 2011, 33(2): 59-61.

[9] 丁荣涛. 基于协作能力约束的港口集卡调度优化策略[J].清华大学学报: 自然科学版, 2012, 52(8): 1158-1164.

[10] 李广儒, 杨大奔, 任大伟. 集卡动态调度路径优化算法[J].交通运输工程学报, 2012, 12(3): 86-91.

[11] 计明军, 靳志宏. 集装箱码头集卡与岸桥协调调度优化[J].复旦学报: 自然科学版, 2007, 46(4): 476-480.

[12] Cao Jinxin, Shi Qinxin, Lee D H. Integrated Quay Crane and Yard Truck Schedule Problem in Container Terminals[J]. Tsinghua Science and Technology, 2010, 15(4): 467-474.

[13] Laborie P, Rogerie J. Reasoning with Conditional Timeintervals[C]//Proc. of the 21st International Conference of the Florida Artificial Intelligence Research Society. Coconut Grove, USA: Florida AI Research Society, 2008: 555-560.

[14] Baptiste P, Laborie P, le Pape C, et al. Constraint-based Scheduling and Planning[M]//Rossi F, van Beek P, Walsh T. Handbook of Constraint Programming. [S. l.]: Elsevier, 2006: 761-794.

编辑 金胡考

Integrated Quay Crane and Yard Truck Scheduling Based on Constraint Programming

QIN Tian-bao, PENG Jia-yao, SHA Mei

(College of Transport & Communications, Shanghai Maritime University, Shanghai 200135, China)

A Mixed Integer Programming(MIP) model and a Constraint Programming(CP) model to tackle the integrated quay crane and yard truck scheduling problem for inbound containers are proposed, which aims to minimize the makespan of unloading process. The CP model is developed with OPL modeling language and employs OPL’s special constructs designed for scheduling problems, e.g., interval variables sequence variable etc. To improve solving efficiency, a special concept called extended operation task is proposed which is used to define interval variables. Besides, a new lower bound is given to evaluate the quality of solutions. Computational experiments on varied scales of instances are carried out to test the CP model and the MIP model. The results indicate that the CP model does not outperform the MIP model for small instances. For medium and large instances, the MIP model can not be solved within time limit, whereas the CP model is effective for finding high-quality solutions and can efficiently solve large problems with fast convergence rate. On average, the gap between the objective values of the CP model and the lower bounds is 2.19%～8.28%.

quay crane scheduling; yard truck scheduling; Constraint Programming(CP); container terminal; optimization; heuristic algorithm; Mixed Integer Programming(MIP)

10.3969/j.issn.1000-3428.2014.05.041

国家自然科学基金资助项目(71172076)；交通部应用基础研究基金资助项目(2011-329-810-450)；上海市科委地方院校专项基金资助项目(11510501800)；上海市教委科研创新基金资助项目(11YZ135)；上海市重点学科建设基金资助项目(S30601)。

秦天保(1971－)，男，副教授、博士，主研方向：港口与航运系统智能优化；彭嘉瑶，硕士研究生；沙 梅，教授、博士。

2013-03-11

2013-06-03E-mail：qtbgo@163.com

1000-3428(2014)05-0196-07

A

TP18