基于模糊阈值补偿的混合蛙跳算法

刘立群，王联国，火久元，韩俊英，刘成忠

(1. 甘肃农业大学信息科学技术学院，兰州 730 070；2. 兰州交通大学电子与信息工程学院，兰州 73007 0)

基于模糊阈值补偿的混合蛙跳算法

刘立群1，王联国1，火久元2，韩俊英1，刘成忠1

(1. 甘肃农业大学信息科学技术学院，兰州 730 070；2. 兰州交通大学电子与信息工程学院，兰州 73007 0)

针对混合蛙跳算法(SFLA)求解复杂问题时收敛速度慢、优化精度低的缺点，提出一种基于模糊阈值补偿的混合蛙跳算法(FTCSFLA)。在SFLA的基础上，采用模糊分组方法对青蛙分组并改进局部搜索的扰动策略。在族群中定义模糊隶属度、隶属度阈值和补偿系数，利用邻域青蛙之间的分布程度衡量某一青蛙的模糊隶属度。在一次局部搜索中，对族群最差个体按模糊隶属度和隶属度阈值关系给出2种更新方法，设置相应的补偿系数。实验结果表明，隶属度阈值为0.9的FTCSFLA其收敛精度、速度均优于SFLA和隶属度阈值为0.5的FTCSFLA，当隶属度阈值取值在(0.5,0.9]之间时，FTCSFLA的性能达到最优。

混合蛙跳算法；模糊隶属度；隶属度阈值；补偿系数；模糊分组；扰动策略；优化性能

1 概述

混合蛙跳算法(Shuffled Frog Leaping Algorithm, SFLA)是模拟青蛙觅食过程中信息共享和交流特点提出的群体智能算法[1-2]，已经成功应用于许多领域。近年来学者们对SFLA优化性能做了诸多改进：文献[3]引入阈值选择策略，通过对不满足阈值条件的个体分量不予更新的策略减小了个体空间差异。文献[4]引入遗传算子增加对局部极值的扰动并借鉴粒子群优化算法中粒子飞行经验对青蛙移动策略进行优化。但是SFLA对于求解复杂问题依然存在收敛速度慢、优化精度低的缺点。这主要是由SFLA的分组方式以及局部更新策略引起的。首先，SFLA在局部搜索前，各青蛙是被逐一循环分配给各个族群的。这种循环分配存在固定性，全局最优个体所在分组更新后得到新的全局最优个体的次数最多，导致该分组寻优能力强于其他分组，一旦该分组陷入局部最优，则整个群体很难跳出局部极值[5]，容易陷入早熟。其次，在局部搜索中，最差个体通过与最优个体的差异进行更新，而这种更新存在随机性，缺乏一定的寻优指导性。这些因素很大程度上影响了SFLA的收敛速度和优化精度。

文献[6-7]将模糊理论引入支持向量机(Support Vector Machine, SVM)中，通过对每个输入样本增加一个模糊隶属度，对含有噪声或野值的样本赋予较小权值，有效提高了SVM分类准确率及计算效率。目前，已有学者将模糊理论与SFLA结合研究：文献[8]在SFLA基础上利用模糊控制器的模糊语言变量及控制规则得出模糊控制表，改进后算法在寻优精度、收敛速度上均有大幅提高；文献[9]将SFLA应用于模糊C均值算法，克服了算法易陷入局部极小的缺陷，提高了算法寻优能力。

为克服SFLA固定循环分配方式容易引起早熟现象的缺陷，并改善局部搜索中的随机性更新，本文将模糊分类思想[6-7]引入SFLA，并借鉴文献[3]固定阈值选择思想，在族群中定义模糊隶属度，设置隶属度阈值对最差个体更新进行适度控制，提出一种新的基于模糊阈值补偿的混合蛙跳算法(Shuffled Fro g L eaping Algorithm Based on Fu zzy Threshold Compensation, FTCSFLA)。

2 SFLA算法

随机生成P=N×M只青蛙组成的初始群体，第i只青蛙个体记为xi=(xi1,xi2,…,xis)，其中，s为个体维数；M为族群数；N为族群内青蛙个数。对每个青蛙个体计算适应度f(xi)，并按f(xi)降序排序，再逐一循环分配给M个族群。对每个族群中f( xi)最差的个体x( k)w按式(1)进行局部搜索：

在式(1)～式(3)中，x( k)w,new和x( k)w,old分别表示族群k中最差个体更新的新旧值；x( k)b表示族群k中局部最优个体；x( g)b表示青蛙群体的全局最优个体；xnew表示定义域内随机产生的一个新个体。对各族群重复局部搜索，直至族群k的局部进化次数T1为止，将所有族群的P个青蛙个体重新混合进行全局信息交换，并按适应度重新排序和划分族群，再对各族群局部迭代，如此反复迭代直至满足问题终止条件或达到全局进化次数T2为止。

3 FTCSFLA算法

3.1 模糊阈值补偿的思想

SFLA局部搜索前的循环分配方式会导致全局最优个体所在分组寻优能力强于其他分组，易使算法陷入早熟。此外，在一次局部搜索中，式(1)、式(2)中最优个体对最差个体的差异扰动rand(0,1)是[0,1]间随机数[10]，存在很大的随机性，没有体现出更好的寻优指导性。针对以上缺陷，本文引入模糊阈值补偿思想，对每个青蛙进行模糊分组，在各分组族群中定义模糊隶属度，设置隶属度阈值，并对局部搜索中最差个体的更新设置补偿系数。以动态模糊的方式调整最差个体的更新程度，以避免局部早熟，达到全局最优。

3.1.1 模糊隶属度

定义1(模糊隶属度) 每个青蛙i(i=1,2,…,N)属于某族群k(k=1,2,…,M)的模糊隶属度记为s(k)i,0＜s(k)i＜1。在一次局部搜索中，每个族群k中f(xi)最差个体x(k)w对应的模糊隶属度记为s(k)w。其中，s(k)i表示第i个青蛙隶属于第k个族群的程度。隶属度越大，它隶属于族群k的可能性越大。因此，族群k是由s(k)i大于某个值的多个青蛙组成的。

3.1.2 模糊隶属度的确定

在生成的P=N×M个青蛙初始群体中，对第k(k= 1,2,…,M)个族群随机选择N个青蛙作为邻域青蛙，利用邻域青蛙之间的分布程度衡量某一青蛙的模糊隶属度，并采用欧氏距离度量两青蛙间距离。则邻域青蛙内第i(i= 1,2,…,N)个青蛙x(k)i的模糊隶属度通过下式确定：

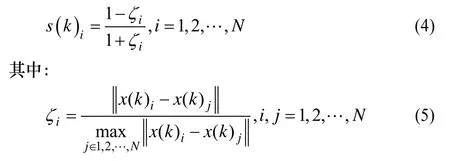
3.1.3 隶属度阈值

定义2(隶属度阈值) 某青蛙i隶属于某族群k的隶属程度由其s(k)i是否大于某一隶属度阈值表示，该隶属度阈值记为s0,0＜s0＜1。

如果s( k)i≥s0，表示青蛙i隶属于族群k的程度大，认为青蛙i隶属于族群k。否则，表示隶属于族群k的程度小，认为青蛙i不隶属于族群k。

在一次局部搜索中，对族群k定义如下：

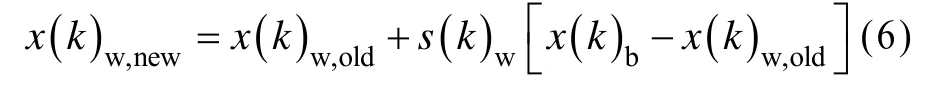
如果按式(6)更新仍无法提高寻优指导性，则使用式(7)进行局部搜索：

扰动策略1如果青蛙i隶属于某族群k，即s( k)i≥s0，则该族群最差个体x( k)w按式(6)局部最优个体x( k)b进行差异扰动。否则，按式(7)全局最优个体x( g)b进行差异扰动。

证明：如果s( k)i≥s0，也即s( k)w≥s0时，说明最差个体x( k)w隶属于族群k，因此，使用式(6)局部最优个体x( k)b进行差异扰动体现了局部寻优指导能力。下面分2种情况证明扰动策略1后半部分：第1种情况：如果s( k)i＜s0，也即s( k)w＜s0时，那么最差个体x( k)w不属于族群k，局部最优个体x( k)b已无法提高寻优性能，使用式(7)全局最优个体x( g)b进行差异扰动体现了全局寻优指导能力。式(7)中1-s( k)w表示不属于族群k的最差个体对应的模糊隶属度。第2种情况：如果s( k)i≥s0，也即s( k)w≥s0时，若按式(6)对x( k)w更新后，如果仍有f( x( k)w,new)≥f( x( k)w,old)，说明式(6)用局部最优个体进行差异扰动无法找到最优值，因此，应按第1种情况最差个体x( k)w不隶属于族群k对待。证毕。

扰动策略1利用模糊隶属度及隶属度阈值之间关系对青蛙群体模糊分组，克服了SFLA固定循环分配方式易引起早熟的缺陷；同时，在一次局部搜索中，分别利用局部最优个体x( k)b、全局最优个体x( g)b对x( k)w的寻优进行指导，避免了式(1)、式(2)随机性更新的缺陷。

3.1.4 补偿系数

定义3(补偿系数) 为统一表示式(6)、式(7)最优个体对最差个体的寻优指导能力，对每个族群k定义补偿系数，记为m( k),m( k)∈{0,1}。

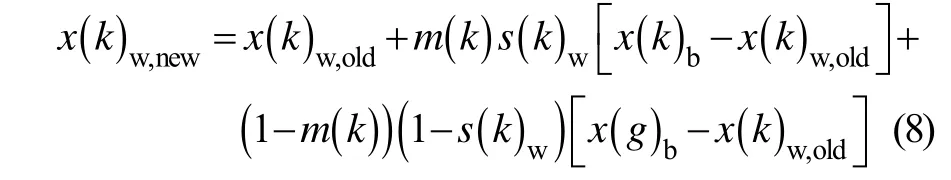
其中，1-m( k)表示使用局部最优个体差异扰动仍无法达到最优时，全局最优个体对差异扰动的寻优补偿能力。

综上，在一次局部搜索中，FTCSFLA将按扰动策略2进行最差个体更新。

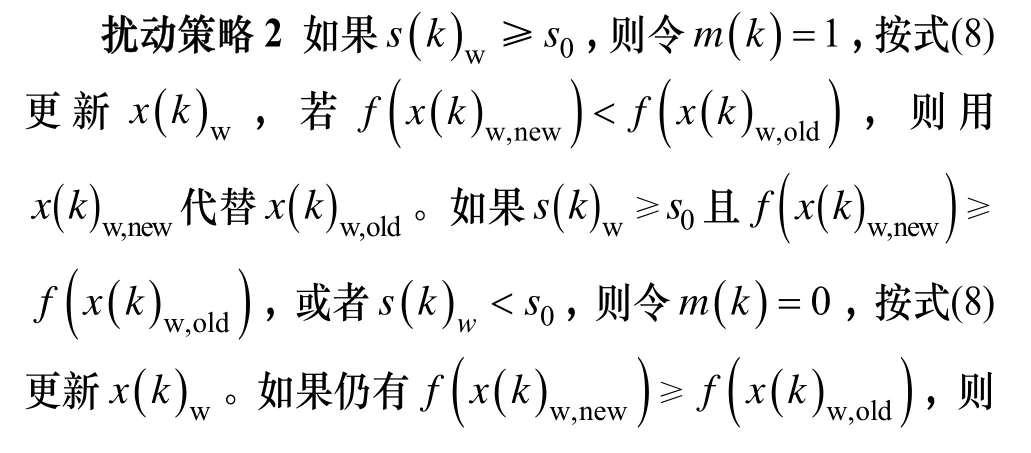
3.2 算法步骤

FTCSFLA是引入模糊隶属度、隶属度阈值及补偿系数等概念，并将模糊阈值补偿的思想应用于SFLA，算法的具体步骤如下：

Step1随机生成P=N×M只青蛙的初始群体，记为XP={xi|xi=(xi1,xi2,…,xis),i=1,2,…,P}，其中，s为个体维数；M为族群数；N为族群内青蛙个数。

Step2设置隶属度阈值s0，并令初始补偿系数m( k)为1，对每个青蛙个体计算适应度f( xi)，并按式(4)计算第k( k=1,2,…,M)个族群的第i( i=1,2,…,N )个青蛙x( k)i的模糊隶属度s( k)i，将P个青蛙模糊分组到M个族群中。

Step3对族群k中f(xi)最差的个体x( k)w进行局部搜索：

Step3.1按f( xi)降序排序，确定x( k)w、x( k)b、x( g)b及x( k)w对应的s( k)w。

Step3.2根据扰动策略2对x( k)w进行更新，计算x( k)w,new。

Step4判断各族群局部进化次数是否达到T1，若未达到，转至Step3。否则，判断青蛙族群全局进化次数是否达到T2或x( g)b是否达到收敛精度，若未达到，转至Step2进行全局信息交换，否则，算法停止，输出x( g)b。

3.3 算法效率分析

FTCSFLA算法的改进主要是在SFLA基础上引入了模糊隶属度、隶属度阈值及补偿系数，算法效率的改进体现在以下3点：

(1)Step2中计算s( k)i并模糊分组，计算只在外层循环中增加T2×M×N次操作时间。

(2)Step3.1对每个族群按f( xi)降序排序，排序由原来的外层循环T2次改变为内层循环T1×M次。

(3)Step3.2中根据改进的局部搜索策略更新x( k)w。增加了比较s( k)w≥s0和s( k)w＜s0的2T1次。

SFLA算法的时间复杂度是O( T1×T2×M×s+T2)，空间复杂度是O( M×N×s)。而FTCSFLA算法的时间复杂度是O( T1×T2×M×s+T2×M×N+T1×M+2T1)，空间复杂度是O( M×N×s+M×N +2)。由于T1＜＜T2，因此FTCSFLA与SFLA的效率是同数量级的，并未增加大的运算开销和空间。

4 实验及结果分析

实验采用Sphere、Rastrigrin、Griewank和Ackley[11-12]4个测试函数作为青蛙个体适应度，分别对SFLA和FTCSFLA算法进行极小值寻优性能测试，并对FTCSFLA算法的隶属度阈值s0设置不同取值进行对比实验。实验参数设置如下：青蛙群体规模P=200，族群数M=20，族群内青蛙个数N=10，各测试函数对应青蛙个体维数s=30，T1=10，T2=500。设置s0=0.9和s0=0.5，分别对应算法FTCSFLA0.9和FTCSFLA0.5。实验所用计算机处理器为Intel Core2，主频为2.0 GHz，内存为2.0 GB，测试平台是VC++6.0。最终测试结果采用独立运行30次后的平均值。

算法性能评价采用如下方法：(1)固定全局进化次数，评价算法收敛精度和速度；(2)固定收敛精度，评价算法达到该精度所需的全局进化次数；(3)不同的隶属度阈值对应的FTCSFLA之间优化性能比较。

4.1 固定全局进化次数的收敛精度和速度分析

各算法收敛精度比较如表1所示，4个测试函数在固定全局进化次数条件下函数平均最优值进化曲线比较如图1～图4所示，其中，fitness代表适应度。

表1 固定全局进化次数结果比较

图1 Sph ere函数平均最优值进化曲线比较

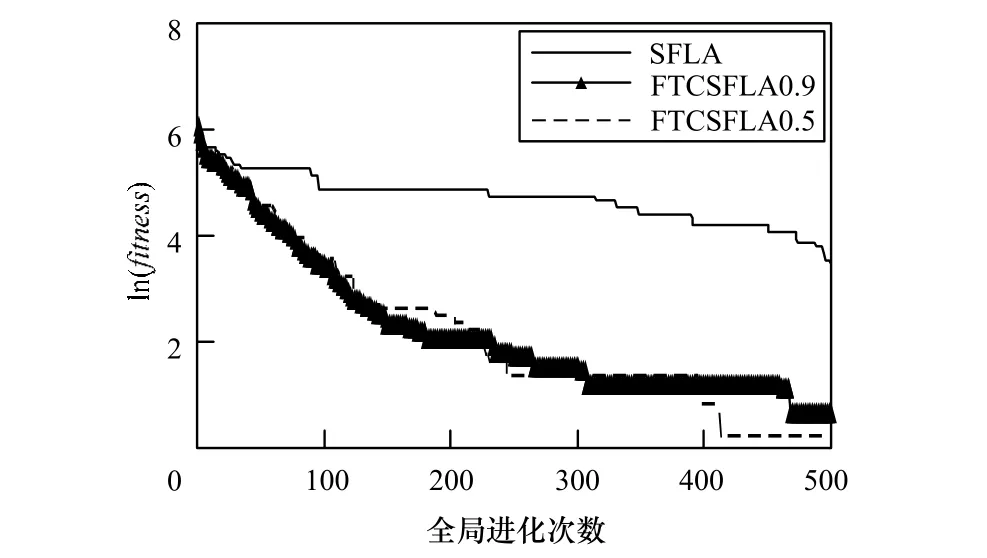
图2 R astrigrin函数平均最优值进化曲线比较

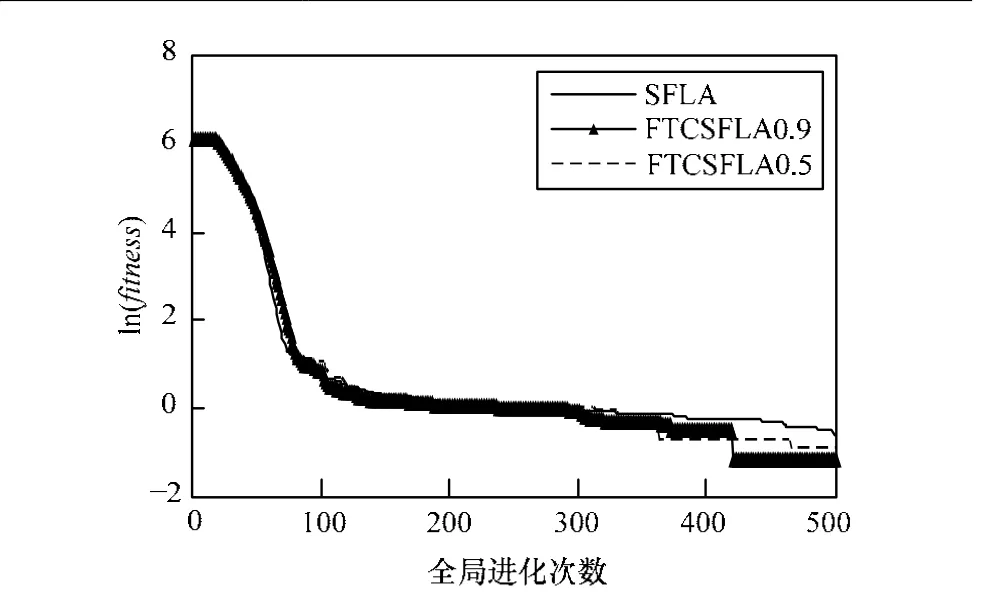
图3 G riewank函数平均最优值进化曲线比较

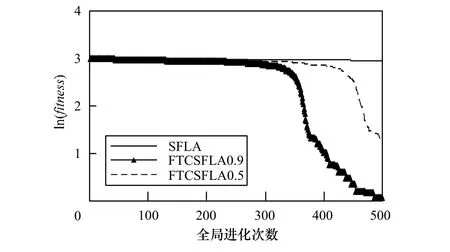
图 4 A ckley函数平均最优值进化曲线比较

可以看出，本文算法各项数值上均优于SFLA，进化曲线也表明其收敛速度均优于SFLA。对单峰值Sphere函数，FTCSFLA0.9和FTCSFLA0.5均达到了理论极小值0，图1显示，FTCSFLA0.9进化到184次时就达到了极小值，FTCSFLA0.5进化到205次时也达到了极小值。由于这2个算法的收敛速度很快，因此在图1中只显示了达到极小值之前的进化曲线，此后没有再显示进化曲线表示算法已经收敛为极小值。对多峰值Rastrigrin、Griewank和Ackley函数，因隶属度阈值s0的调节，使得青蛙隶属于不同族群的程度发生了变化，FTCSFLA0.9和FTCSFLA0.5的收敛精度有上下浮动，从进化曲线表明隶属度阈值s0取值范围在(0.5, 0.9]之间FTCSFLA收敛精度和收敛速度最为理想。

4.2 固定收敛精度的全局进化次数分析

4个测试函数目标精度和各函数达到目标精度时的平均进化次数见表2[11-12]。实验结果表明，FTCSFLA0.9达到目标精度的次数明显少于SFLA和FTCSFLA0.5。

表2 固定收敛精度结果比较

以上2个不同角度的对比结果表明，FTCSFLA0.9收敛精度、速度均优于SFLA和FTCSFLA0.5，并且FTCSFLA在隶属度阈值取值范围在(0.5,0.9]之间时其收敛精度和速度为最优。

5 结束语

本文提出一种基于模糊阈值补偿的混合蛙跳算法，引入模糊阈值补偿思想，对青蛙模糊分组，在族群中定义了模糊隶属度、隶属度阈值和补偿系数等概念。在局部搜索中，设置隶属度阈值，根据模糊隶属度和隶属度阈值关系，给出了2种最差个体的更新方法，并设置补偿系数统一表达了2种更新方法。该算法以动态模糊的方式调整最差个体的更新程度，避免了局部早熟。实验结果表明，该算法在单峰值和多峰值函数寻优问题上均具有较高的收敛速度和精度，改进了SFLA的优化性能。未来将进一步研究动态隶属度阈值对算法性能的影响。

[1] Eusuff M M, Lansey K E. O ptimization of Water Distribution Network Design Using the Shuffled Frog Leaping Algorithm[J]. Journal of Water Sourc es Planning an d M anagement, 2003, 129(3): 210-225.

[2] Eusuff M M, Lansey K E, Pasha F. Shuffled Frog Leaping Algorithm: A Memetic Meta-heuristic for Discrete O ptimization[J]. Engineering Optimization, 2006, 38(2): 129-154.

[3] 李英海, 周建中, 杨俊杰, 等. 一种基于阈值选择策略的改进混合蛙跳算法[J]. 计算机工程与应用, 2 007, 43(35): 19-21.

[4] 欧 阳, 孙元姝. 基于改进混合蛙跳算法的网格任务调度策略[J]. 计算机工程, 2011, 37(21): 146-148.

[5] 代永强, 王联国. 带记忆功能的混合蛙跳算法[J]. 计算机工程与设计, 2011, 32(9): 3170-3173.

[6] L in Chunfu, Wang Shengde. Fuzzy Support Vector Machines[J]. IEEE Transcations on Neural Networks, 2002, 13(2): 464-471.

[7] Huang Hanpang, Liu Y H. Fuzzy Support Vector Machines for Pattern Recognition and Data Mining[J]. International Journal of Fuzzy Systems, 2002, 4(3): 826-835.

[8] 葛 宇, 王学平, 梁 静. 改进的混合蛙跳算法[J]. 计算机应用, 2012, 32(1): 234-237.

[9] 赵小强, 刘悦婷. 基于选择和变异机制的蛙跳FCM算法[J].计算机应用研究, 2012, 29(6): 2068-2071.

[10] 王 辉. 一种带共享因子的人工蜂群算法[J]. 计算机工程, 2011, 37(22): 139-142.

[11] 王 凌. 智能优化算法及其应用[M]. 北京: 清华大学出版社, 2001.

[12] Engelbrecht A P. F undamentals of Computational Swarm Intelligence[M]. 谭 营, 译. 北京: 清华大学出版社, 2009.

编辑 金胡考

Shuffled Frog Leaping Algorithm Based on Fuzzy Threshold Compensation

LIU Li-qun1, WANG Lian-guo1, HUO Jiu-yuan2, HAN Jun-ying1, LIU Cheng-zhong1

(1. College of Information Science and Technology, Gansu Agricultural University, Lanzhou 730070, China; 2. School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

To solve the problem of slow convergence speed and low optimization precision of Shuffled Frog Leaping Algorithm (SFLA) in solving complex problems, a Shuffled Frog Leaping Algorithm Based on Fuzzy Threshold Compensation(FTCSFLA) is proposed. The fuzzy grouping idea is introduced to divide different frogs into fuzzy groups, and disturbance strategy in a local search is improved based on the basic SFLA. Each fuzzy group is defined with a total membership threshold and a total compensation coefficient, and each frog is defined with a fuzzy membership, which is scaled with the distribution degree of neighborhood frogs. In a local search, the worst individual is updated by two methods in each group, which is partitioned ac cording to the relation between fuzzy membership and membership threshold. In t wo methods, a com pensation coefficient is set to gi ve a u nify expression. Experimental results show th at the con vergence precision and speed of FTCSFLA which membership threshold is 0.9 is better than SFLA and FTCSFLA which membership threshold is 0.5. The evolution curve shows that the convergence precision and speed of FTCSFLA is the optimum when its membership threshold is between (0.5, 0.9].

Shuffled Frog Leaping Algorithm(SFLA); fuzzy membership; membership threshold; compensation coef ficient; fuzzy grouping; disturbance strategy; optimization performance

10.3969/j.issn.1000-3428.2014.05.035

国家自然科学基金资助项目(61063028)；中国博士后科学基金资助项目(2013M542398)；甘肃省高等学校研究生导师科研基金资助项目(1202-04, 1 102-05)；甘肃省教育厅信息化战略研究基金资助项目(2011-02)；甘肃省自然科学研究计划基金资助项目(1308RJZA214, 1208RJZA133)；甘肃农业大学盛彤笙科技创新基金资助项目(GSAU-STS-1322)；兰州交通大学青年科学基金资助项目(2013032)。

刘立群(1982－)，女，讲师、硕士，主研方向：群体智能算法，数据库技术；王联国，教授、博士；火久元，副教授、博士；韩俊英，副教授、硕士；刘成忠，副教授、博士研究生。

2013-03-04

2013-05-27E-mail：llqhjy@126.com

1000-3428(2014)05-0168-05

A

TP18