CS-MRI中稀疏信号支撑集混合检测方法

冯 振，郭 禾，王宇新，贾 棋，侯广峰

(1. 大连理工大学软件学院，辽宁 大连 1 16620；2. 大连理工大学计算机科学与技术学院，辽宁 大连 1 16024)

CS-MRI中稀疏信号支撑集混合检测方法

冯 振1，郭 禾1，王宇新2，贾 棋1，侯广峰1

(1. 大连理工大学软件学院，辽宁 大连 1 16620；2. 大连理工大学计算机科学与技术学院，辽宁 大连 1 16024)

针对磁共振成像技术采样过程过慢的问题，给出一种新的基于压缩感知的图像重建方法。通过分析一种特殊的基于奇异值分解(SVD)的信号稀疏表示方法，提出一种结合稀疏信号位置和大小信息的支撑集混合检测方法，并根据该方法改进稀疏信号重建算法FCSA。实验结果证明，在相同的欠采样率下，改进FCSA算法重建图像的峰值信噪比(PSNR)比传统的基于小波稀疏基的FCSA算法重建图像的PSNR高2.21 dB～12.72 dB，比基于SVD稀疏基的FCSA算法重建图像的PSNR高0.87 dB～2.05 dB，且重建时间从基于小波稀疏基的FCSA算法的103.21 s下降至改进FCSA算法的36.91 s。

压缩感知；磁共振成像；支撑集检测；奇异值分解；稀疏信号；FCSA算法

1 概述

基于压缩感知的磁共振成像技术(Compressed Se nsing-Magnetic Resonance Imaging CS-MRI)能够以远低于奈奎斯特频率的采样频率对目标信号进行采集，从而极大降低采样时间[1-2]。该技术自提出以来，得到学术界和工业界的广泛关注。目前对CS-MRI的研究已经扩展到磁共振成像技术的各方面，如压缩感知方法与并行成像技术的结合[3]、与动态磁共振成像的结合[4]、与三维磁共振成像的结合[5]等。

FCSA(Fast C omposite Splitting Al gorithm)是一种有效的CS-MRI图像重建方法[6]，实验结果表明，在同等欠采样频率和相似重建时间下，该方法能获得比CG算法[7]、TVCMRI算法[8]和RecPF算法[9]等更好的重建效果。本文提出了一种基于支撑集检测的FCSA方法(FCSA w ith Support)，该方法采用一种特殊的基于奇异值分解(Singular Value Decompo sition, SVD)的信号稀疏化方法[10]，并根据SVD稀疏信号的分布特性给出一种结合信号位置和大小信息的支撑集检测方法。

2 CS-MRI方法

2.1 基于支撑集检测的CS-MRI技术

在CS-MRI技术框架下，磁共振图像可以通过满足以下约束条件重建：

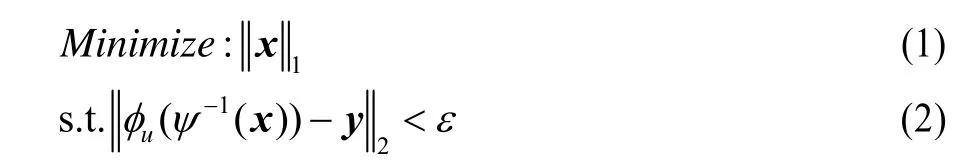
其中，矩阵x是磁共振图像m经过稀疏变换ψ得到的稀疏信号，即ψ-1(x)=m；uφ是欠采样傅里叶变换，即首先对图像m做傅里叶变换，然后欠采样k空间信号；y是磁共振线圈采集到的k空间信号；ε则和线圈采样过程中的噪音误差相关。式(1)约束了信号的稀疏性，式(2)约束了信号的数据一致性。

基于支撑集检测的CS-MRI技术是对传统CS-MRI技术的一个改进，该技术利用了稀疏信号在一些先验知识，即稀疏信号在某些已知的位置是非零的，或具有较大的信号值，则在做信号稀疏性约束时，便不需要考虑这些位置的信号。设这些已知位置的集合，即支撑集为Τ，信号中其他位置为Δ，则基于支撑集检测CS-MRI技术可以通过约束以下条件重建磁共振图像：

其中，xΔ表示了稀疏信号x中除支撑集Τ以外位置的信号。

2.2 结合信号位置和大小信息的支撑集检测方法

求解稀疏信号的支撑集T是一个迭代求解不断精确化的过程，前人的工作表明，支撑集T越精确，在同样欠采样频率下重建出的图像越好。支撑集有2种检测方法：

(1)基于信号位置的方法，如文献[11]在时域傅里叶信号的中心位置指定一个矩形作为为支撑集。

(2)基于信号大小的阈值方法，有2种阈值设定方法[12]：

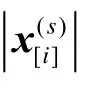
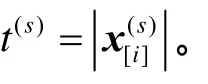
传统的CS-MRI技术使用小波变换作为稀疏基，而本文采用一种特殊的基于SVD的磁共振图像稀疏表示方法。设m是目标磁共振图像，mu是m在k空间欠采样后得到的图像。对mu做SVD分解：

研究人员发现，欠采样图像mu的SVD矩阵Uu和Vu可以作为全采样图像m的稀疏基[10]，即：

如图1所示，图1(a)是全采样图像m，图1(b)是欠采样图像mu，欠采样率为1/5，图1(c)表示了m的稀疏信号Sm。可以看出，基于SVD的磁共振图像稀疏表示具有极强的分布特性，稀疏信号的较大值集中在了图像的左上角和对角线附近。据此，本文提出一种结合稀疏信号位置和大小信息的支撑集检测方法。

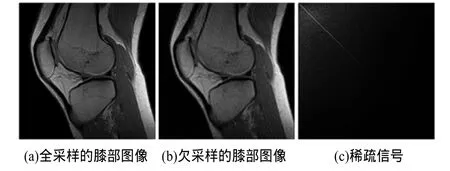
图1 S VD分解图像的稀疏表示方法

设所有位置信号的集合为Α：(1)根据信号的位置信息，即该信号与原点及对角线的距离，将该信号划分为Α1和Α2，其中，A1距离原点及对角线的距离小于某个给定的阈值，Α2=Α/ Α1；(2)使用显著第一跳的方法确定本次迭代的阈值t(s)，在Α1集合中大于阈值t(s)的信号集合作为本次迭代的支撑集T，Α1中小于阈值t(s)的信号的集合与Α2的并集组成信号集合Δ，即Δ=A1/T+A2。

本文采用以下方法将信号集合Α划分为Α1和Α2。设稀疏信号的一个像素点为xi，xi与原点(original)的欧式距离为，xi与对角线(diagonal)的欧式距离为，则xi的位置信息权值表示为其中，α, β是 2种距离的权值，且α, β＞0。

2.3 基于支撑集的FCSA算法

为重建磁共振图像，FCSA算法将式(1)转变为以下重建问题：

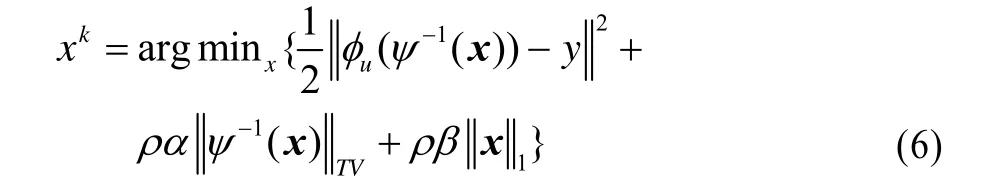
其中，k是迭代重建的次数；TV是对磁共振图像的全变分操作；ρ、α和β是数据一致性、信号全变分稀疏性和信号L1稀疏性的平衡因子。

FCSA算法首先将变量x分裂为x1和x2，然后对x1和x2独立地执行运算符分裂，最后将更新后的x1和x2线性组合在一起得到更新后的x。

基于支撑集的FCSA算法将式(6)转换为以下重建问题：

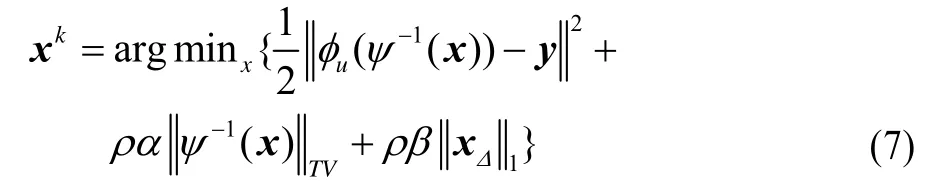
该算法可以采用类似于FCSA算法中变量分裂和运算符分裂的方法重建信号x。

3 实验与结果

全部实验在一台笔记本上进行，硬件配置为Intel i 7-3612QM处理器，6 GB内存，软件环境为Windows 7 64位，Matlab R2008a。

采用2幅磁共振图像作为测试集，一幅为膝部图片，如图2(a)所示；一幅为乳房图片，如图2(b)所示。2幅图片均由西门子公司1.5T磁共振系统采集获得。将磁共振图像在k空间内欠采样，欠采样模板如图3所示。在实验中，欠采样率设置为1/4、1/5和1/6。作为对比实验，共使用了3种算法重建欠采样图像，即以小波变换(Daubechies-4)为稀疏基的FCSA算法(FCSA with Wavelet)、以SVD为稀疏基的FCSA算法(FCSA with SVD)和基于支撑集的FCSA算法(FCSA with Support)。

图2 磁共振图像

图3 k空间欠采样模板

表1记录了上述3种算法在不同欠采样率下重建得到的图像的峰值信噪比(PSNR)。对相同的欠采样图像，FCSA with SVD算法和FCSA with Support算法都获得了比FCSA with Wavelet算法更高的PSNR值。相比于FSCA with SVD算法，FCSA with Support算法根据检测到的支撑集进一步约束了信号的稀疏性，因此后者获得了更高的PSNR值。

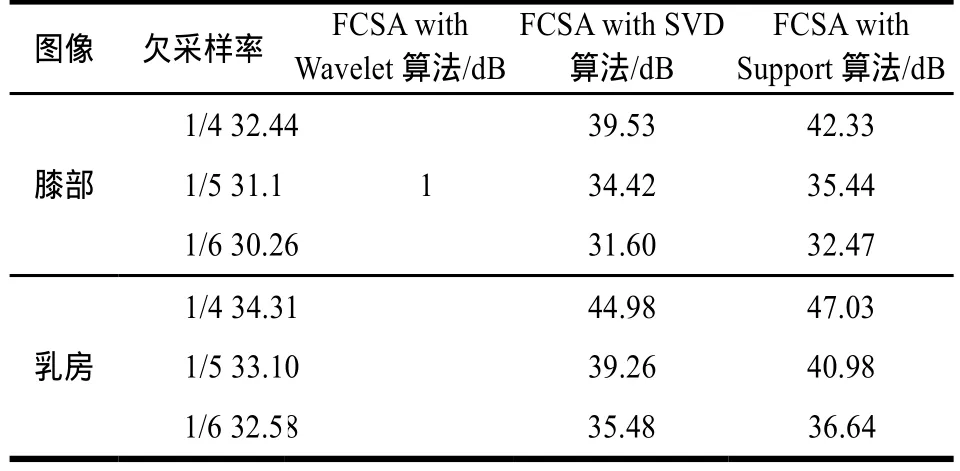
表1 重建图像峰值信噪比

图4显示对欠采率为1/4的膝部图像的重建效果。图5显示对欠采样率为1/4的乳房图像的重建效果。第1行为重建的图像；第2行为重建图像与原始图像的差值图，为更清晰地显示重建错误，图中差值均扩大了5倍。

图4 欠采样率为1/4的膝部图像的重建效果

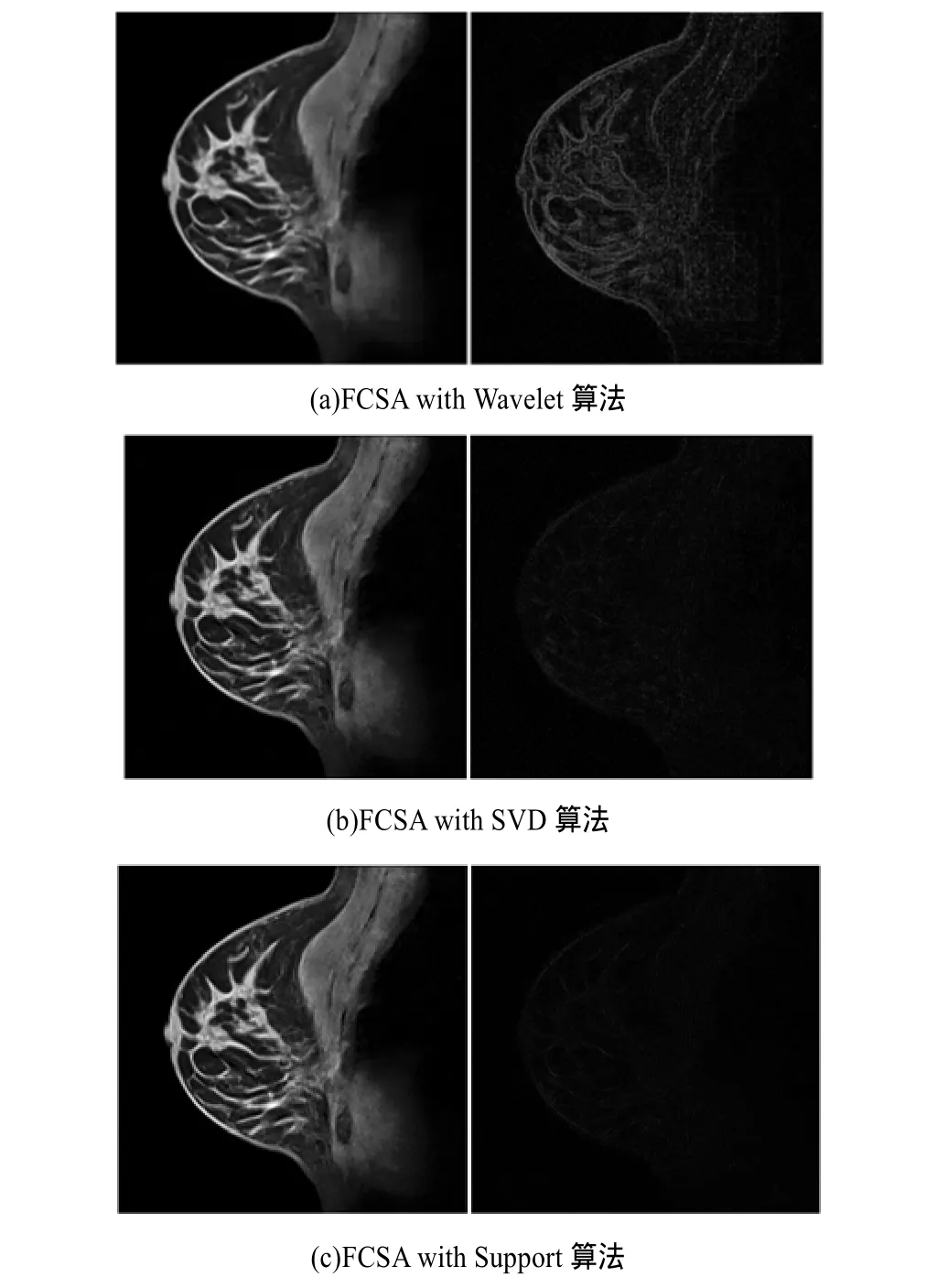
图5 欠采样率为1/4的乳房图像的重建效果

从图4、图5可以看出，FCSA with SVD方法和FCSA with Support方法能够比FCSA with Wavelet方法重建出质量更好的图像；同时也可以看出FCSA with Support方法重建的图像具有比FCSA with SVD方法重建的图像更小的重建错误。

表2比较了上述3种方法对膝部和乳房图像重建时，在不同欠采样率下的平均重建时间。在实验中，FCSA算法的迭代次数统一设置为50次，不同的信号稀疏变换方法导致了重建时间的差异。FCSA wi th W avelet方法使用了Daubechies-4小波作为稀疏基，实验发现对512×512的矩阵执行Daubechies-4小波变换的平均时间为0.51 s；FCSA with SVD方法和FCSA with Support方法使用的基于SVD的信号稀疏方法需要对3个矩阵做2次连续的矩阵乘法运算，实验发现对3个512×512的矩阵执行2次连续矩阵乘法的平均时间为0.009 s，远小于小波变换所需时间；因为FCSA with Support方法在约束信号稀疏性时需要在全部信号中选择非支撑集信号，通过稀疏信号点乘以2值矩阵执行该选择操作，2值矩阵中0值表示支撑集信号的位置，该矩阵点乘操作(平均0.001 s)导致FCSA with Support方法比FCSA with SVD方法的执行时间略长。

表2 图像重建平均时间 s

4 结束语

本文根据基于SVD稀疏基的磁共振图像稀疏表示，提出一种结合了稀疏信号位置和大小信息的支撑集检测方法，并根据该方法改进了FCSA重建算法。本文实验证实，对于某些稀疏信号，其特殊的信号分布特性可以作为一种有效的先验知识用于欠采样信号的重建。今后的研究重点有2个研究方向：(1)针对其他的稀疏基，研究其稀疏信号的分布特征，提出优化的支撑集检测方法；(2)本文方法经过扩展，可以应用到解决磁共振并行成像、动态成像和三维成像等问题中。

[1] 戴琼海, 付长军, 季向阳. 压缩感知研究[J]. 计算机学报, 2011, 34(3): 425-434.

[2] 侯金曼, 何 宁, 吕 科. 基于压缩感知的图像快速重建方法[J]. 计算机工程, 2011, 37(19): 215-217, 226.

[3] Block K T, Uecker M, Frahm J. Un dersampled Radial MRI with Multiple Coils. Iterative Image Reconstruction Using a Total V ariation Constraint[J]. Magnetic Resonance in Medicine, 2007, 57(6): 1086-1098.

[4] Lustig M, Santos J M. k-t Sparse: High Frame Rate Dynamic MRI Exploiting Spatio-temporal Sparsity[C]//Proc. of International Soc iety for Mag netic Resonance in Medicine. Seattle, USA: [s. n.], 2006: 2420- 2426.

[5] Bilgin A, Trouard T P, Altbach M I, et al. Three-dimensional Compressed Sensing for Dynamic MRI[C]//Proc. of International Soc iety for Mag netic Resonance in Medicine. Toronto, Canada: [s. n.], 2008: 337-345.

[6] Huang Ju nzhou, Z hang Sha oting, Metaxas D. Efficient MR Image Re construction for Compressed MR Imaging[J]. Medical Image Analysis, 2011, 15(5): 670-679.

[7] Lustig M, Donoho D L, Pauly J M. S parse MRI: The Application of Compressed Sensing for Rapid MR Imaging[J]. Magnetic Resonance in Medicine, 2007, 58(6): 1182-1195.

[8] Ma Shiqian, Y in W otao, Zhang Yin, et al. An Efficient Algorithm for Compressed MR Imaging Using Total Variation and Wavelets[C]//Proc. of IE EE Conferen ce o n Computer Vision and Pattern Recognition. Anchorage, USA: Institute of Electrical and Electronics Engineers Computer Society, 2008: 233-239.

[9] Y ang Junfe ng, Zh ang Y in, Yin Wotao. A F ast Alternating Direction Metho d for TVl1-l2 S ignal Reco nstruction From Partial Fourier Data[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 288-297.

[10] Hong Ming jian, Yu Yeyang, Wang Hua, et al. Compressed Sensing M RI with Sing ular Value Dec omposition-based Sparsity Basis[J]. Physics in Me dicine and Biolo gy, 20 11, 56(1): 6311-6325.

[11] Liang Dong, L Y ing. Co mpressed-sensing Dynamic MR Imaging Using Partially Kno wn Su pport[C]//Proc. of IEE E Engineering in Medicine an d Biology Confere nce. Buen os Aires, Argentina: IEEE Computer Society, 2010: 2829-2832.

[12] W ang Y ilun, Yin Wotao. Sparse Signal Re construction via Iterative Support Detection[J]. SIAM J Imaging Science, 2010, 3(3): 462-491.

编辑 索书志

Hybrid Detection Method of Sparse Signal Support Set in CS-MRI

FENG Zhen1, GUO He1, WANG Yu-xin2, JIA Qi1, HOU Guang-feng1

(1. School of Software Technology, Dalian University of Technology, Dalian 116620, China; 2. School of Computer Science and Technology, Dalian University of Technology, Dalian 116024, China)

Aiming at the problem of slow sampling time in Magnetic Resonance Imaging(MRI), a new Compressed Sensing(CS) method is proposed. Singular Value Decomposition(SVD)-based sparse representation is an effective but not widely studied method in the CS-MRI field. This sparse representation is improved using the partially known signal sup port method. A hybrid support d etection method is proposed to make use both the position and magnit ude knowledge of the sparse signals. This hybrid support detection method is f urther applied in Fast Composite Splitt ing Algorithm(FCSA), which is an effective reconstruction algorithm for CS-MRI problem. Experimental results show that the proposed FCSA algorithm outperforms the FCSA with Wavelet method and the FCS A with SVD method in th e reconstructed image qualities, its PSNR is 2.21 dB～12.72 dB higher than the FCSA with Wavelet method, 0.87 dB～2.05 dB higher than the FCSA with SVD method, and the reconstruction time is 36.91 s compared with 103.21 s of the FCSA with Wavelet method.

Compressed Sensing(CS); Magnetic Resonance Imaging(MRI); support set detection; Singular Value Decomposition(SVD); sparse signal; FCSA algorithm

10.3969/j.issn.1000-3428.2014.05.034

国家自然科学基金资助重点项目(61033012)；国家自然科学基金资助项目(61003177)。

冯 振(1987－)，男，博士研究生，主研方向：图像处理；郭 禾，教授；王宇新，副教授；贾 棋，讲师；侯广峰，助教。

2013-04-10

2013-06-03E-mail：fengz@mail.dlut.edu.cn

1000-3428(2014)05-0164-04

A

TP18