大整数取模的快速运算

许鑫，李顺东

陕西师范大学计算机科学学院，西安 710062

大整数取模的快速运算

许鑫，李顺东

陕西师范大学计算机科学学院，西安 710062

1 引言

大整数取模运算在公钥密码学中具有重要的实际应用价值，如RSA[1]算法。在进行大量的加密/解密运算时，大整数取模运算是制约RSA算法效率的主要因素，这使得RSA算法的计算复杂度较高，在与相同安全级别的对称加密算法[2]相比时，RSA算法的运算效率很低。因此，在公钥密码学中，对大整数取模算法的改进具有重要的实用价值。传统的大整数取模运算步骤主要是一个试商的过程，即每一次试商都需要做一次遍历，每次遍历中还需要做乘法和试减运算，使得时间复杂度为O(n2)，效率很低。因此提出了很多种对大整数取模运算的改进算法，如蒙哥马利（Montgomery）[3]算法和欧几里德除法[4]等，但都没有达到理想的效果。

本文另辟蹊径，依据分治法[5]思想，提出一种改进大整数取模运算的快速算法，将原来的遍历运算转换成8次大整数乘法运算和准确试商运算，使得计算复杂度降低到O(n(m-n))，极大地提高了大整数取模运算的效率，从而改进和优化RSA算法。

2 大整数取模快速算法

2.1 大整数取模算法

大整数取模运算需要进行乘法和减法两个步骤，对每一位的商都要重复这两个步骤。设有m位和n位两个大整数A和B(m＞n＞1)，取模运算表示成：

首先截取大整数A的前n位对大整数B进行试减运算，然后将大整数A的第n+1位添加至余数的末尾组成新的被除数，如此循环，直至最后的余数小于大整数B，此时的余数即是最后的结果C。算法步骤如下：

其中B1存放试减的数，C为每次试减后的结果，for循环结束后即为最后的余数。由于遍历需要m-n次，每次需要8次乘法，而这8次乘法都是重复地与大整数B进行相乘，因此，可以用查找表代替重复运算来改进算法。

2.2 改进算法的核心思想

大整数取模是一个运算量极大的数学运算，因为当n很大时，传统的大整数取模算法效率极为低下。蒙哥马利（Montgomery）算法是将幂模运算[6]转换成乘法和移位运算，虽然最后结果看似简单，但是对中间变量的求解是比较复杂的，尤其在RSA算法中，中间变量的不断变化也使此算法的效率降低。文献[7]采用变长滑动窗口方法改进的蒙哥马利算法，虽然提高了模指数运算，但在大整数的取模运算中，过多的乘法次数必然影响其效率。为了提高幂模运算效率，国内外专家学者已经提出了很多改进的算法[8-10]。

在对公钥密码尤其是RSA算法的研究中，可以发现[11-12]：

（1）模运算的结果在运算最后直接获得，不需要另外记录。

（2）面向公钥密码的模运算，每一次的加密/解密运算过程所用到的大整数n是固定不变的，并且是循环使用。因此，对其进行预处理，得到一个预处理表，以便在一次加密/解密过程中多次调用，从而避免重复运算所浪费的时间，降低运算复杂度。

（3）在每次模运算中通过寻找模运算的规律，可以得到每次快速模运算的方法。

在现实中，整数是以十进制进行存储，乘法计算也是以十进制方式表达的，因此本文提出的大整数取模改进算法，是以十进制数据结构进行存储和运算的。

任何一个正整数是由0～9中的一个或多个数字组成，其中首位数字不能为0。例如：设存在一个m位和一个n位大整数A和B(m＞n＞1)，根据分治法思想，对大整数A和B做乘法运算时，

文献[13]提出一种大整数相乘快速算法：将大整数A分解为m个独立整数的组合，这样大整数A和B的乘法运算就是将m个数字(0～9)与大整数B的相乘运算得到的结果存储在一个查找表数组Value[10]中，即Value[0]存储0，Value[1]存储大整数B，Value[2]～Value[9]依次存储数字2～9和大整数B的乘积。然后依次根据大整数A的m位整数进行查表，将乘法结果移位后做加法运算得到最终结果。因此，通过建立查找表的大整数相乘快速算法[13]可将原有的n次乘法运算降低至8次。

设存在一个m位和一个n位大整数A和B(m＞n＞1)，在做大整数取模运算时，

依照上述大整数乘法的分治思想，同样构造一个这样的预处理表：首先将数字(1～9)与大整数B相乘运算的结果存入Value数组中，将结果的最高两位存入aTable数组中，其中carry变量为进位标识，将第一个有乘法进位的数存在aTable数组中的第一位，后面则依次存储，这样可以从小到大排列乘法结果最高两位，由于数字(1～9)与任何一个大整数相乘前两位一定不同，取存储数组aTable中前两位进行比较，构造一个预处理表sTable，其中sTable[x]中记录着aTable数组中最高位为x(x∈Z且x∈[1,9])的数组标识，并根据aTable数组前两位从大到小记录。这样在试商过程中通过比较被除数最高两位和预处理表sTable数组中的数，可直接从Value数组中找到试减的数，然后进行减法运算得到新的被除数。接下来重复刚才的运算，直至最后被除数小于除数，这时的被除数就是最终的取模运算结果。

在每次试除运算中，通过改进的预处理表可以直接找到试减的数，相对于不停地试商以找到试减的数，显然效率更高。上面的方法在效率上将取模转换成查表和减法，而构造的预处理表在一次运算中可以重复利用，极大地提高了运算效率。

2.3 改进算法的实现过程

改进取模算法的原理基于十进制运算，故为了能够精确表示大整数，本文采用定长数组A[m]（数组初始化时为0）存储大整数A，定长数组B[n]存储大整数B，定长二维数组Value[9][n+1]来存储数字(1～9)与大整数B的相乘运算的结果，二维数组aTable[9][2]存储对应的数字(1～9)和上面结果的前两位，以加快构建预处理表sTable[9][9]数组，此表类似一个矩阵，其中行标识试商的数的最高位，列标识准确试商的标志以便通过数组sTable直接在数组Value中找到要试减的数。

例如，大整数A为987 654 321 998 877 662 345，大整数B为56 321 987 213，在做大整数取模运算时，

首先，将数字1～9与大整数B相乘得到Value数组如表1所示。

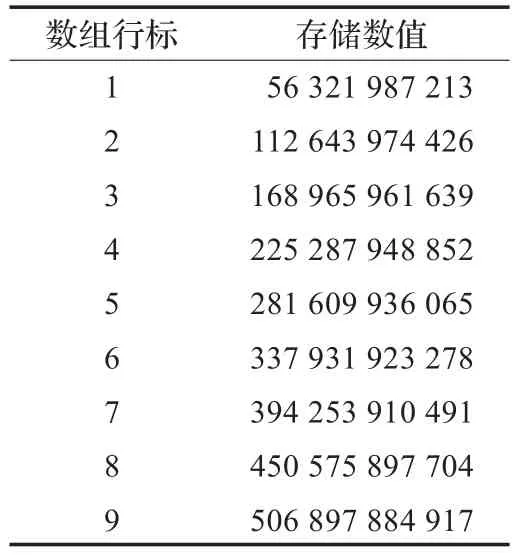
表1 数组Value[9][12]

表1中第1行表示1与大整数B相乘的结果，第2行表示2与大整数B相乘的结果，以此类推，第9行表示9与大整数B相乘的结果。从表1中找到第一个比大整数B的位数大的数组行标，即在第2行有第一个进位，则进位标识carry为2。aTable数组存储每行Value数组的高两位，在建立aTable数组时，从Value[carrymod 9]开始记录，这样保证了aTable数组由小到大排序，如表2所示。

表2 数组aTable[9][2]

表2中第1行表示Value[2]的高两位，第2行表示Value[3]的高两位，以此类推，第9行表示Value[1]的高两位。通过从后向前遍历aTable数组建立预处理表sTable[9][9]（如表3），可以快速在Value数组中找到试减数，避免了每次试除时完全遍历Value数组。检测大整数B的位数为n，取大整数A的前n位按数组下标从1到n赋给数组X[n+1]，可以发现：

（1）与数组X最高位相等的试减数可能有多个，这时必须从大到小逐个试减，若试减数比数组X大，则重新找比这一试减数小的数，进行试减。

（2）在与数组X最高位相等的试减数中，都比数组X大，则必须找到比数组X最高位小1的最大试减数，进行试减。

（3）在数组X最高位与所有试减数不等的情况下，这时必须找到比数组X最高位小且最接近的数组行标，得到最大试减数进行试减。

表3 数组sTable[9][9]

首先，在数组sTable的第i行(1≤i≤9)，从后向前遍历aTable数组中第1列为i的数组行标x(x∈Z且x∈[1,9])，经过运算(x+carry-1) mod 9后，依次将值存储在此行（从大到小存储试减数与数组X最高位相等时的数组行标）；其次，从前向后遍历aTable数组，得到第一个与i相等的数组行标x′(x′∈Z且x′∈[1,9])，经过运算(x′+carry-2) mod 9后（若为0，则改为9），将值存储在此行的下一列（在上一步存储过程结束后的下一列，存储试减数比数组X最高位小1的数组行标）；最后，从前向后遍历sTable数组中全为0的行，依次将其上一行的第一列的值赋予此行第1列，其余为0（在试减数与数组X最高位不相等的情况下，存储比数组X最高位小且最接近的数组行标）。建立好预处理表sTable数组后，在每次试除时，通过比较数组X的最高位和sTable数组行标的关系，得到相应的Value数组行标，从而快速在Value数组中找到试减的数进行减法运算。

表3中第1行表示，从后向前遍历aTable数组中第1列为1的数组行标，得x1=2和x2=1，运算后依次将3和2存储在数组sTable的第1行第1列和第2列；然后，从前向后遍历aTable数组，得到第一个与数组X的最高位相等的数组行标x′=1，运算后将1存储在数组sTable的第1行第3列，以此类推；最后，数组sTable的第6行全为0，则将第5行第1列的值存储在第6行第1列，其余为0，以此类推，直到数组sTable的建立。若数组X最高位为1，则从sTable[1]这一行读取数据，第一个是3，比较大整数A与Value[3]，若A大就减去Value[3]，否则就与Value[2]比较，若A大就减去Value[2]，否则减去Value[1]。算法步骤如下：

例子中，首先检测B的位数为11，则取大整数A的前11位按数组下标从1到11赋给数组X[12]，此时X的最高位为9，在sTable[9]读取sTable[9][1]=1，则比较X与Value[1]，得X＞Value[1]，进行减法运算X=X-Value[1]= 42 443 444 986，此时检测X的位数，若为11，则扩大10倍再加上大整数A的第12位变成424 434 449 868，在上述数组X中，将大整数A的第12位添加至X数组下标的第11位即可（若位数为10，则扩大10倍加上大整数A的第12位后再扩大10倍加上大整数A的第13位，在上述数组X中，将大整数A的第12位和第13位依次添加至X数组下标的第10位和第11位即可）。此时X最高位为4，在sTable[4]读取sTable[4][1]=8，则比较X与Value[8]，得X＜Value[8]，条件失效不进行减法运算，在sTable[4]读取下一个sTable[4][2]=7，则比较X与Value[7]，得X＞Value[7]，进行减法运算X=X-Value[7]= 30 180 539 377，X的位数为11，扩大10倍加上大整数A的第13位，X=301 805 393 778。以此类推，直到大整数A中所有数字都参与完运算，程序结束得到最终取模结果为52 870 988 247。

以上的例子中，在建立sTable表后，最多查找3次必然可以找到试减数进行试减；若没有此表，最多查找9次才可以找到试减数进行试减。查找和比较次数都大大减少，故sTable表的建立提升了算法效率。

改进的算法进行运算时，需要遍历m-n次，每次遍历做O(1)次比较和一次n位减法，得到预处理表时需要8次乘法，以减法运算作为基本运算，乘法时间复杂度为O(1)，可忽略不计，故此算法的时间复杂度为O(n(m-n))，空间复杂度为O(n)。

3 算法效率分析与比较

本文采用Java[14]语言实现了改进的大整数取模算法，实验计算机配置如下：操作系统为Windows 7，CPU为酷睿i3-2330M，2 GB的DDR3内存。

改进的算法核心部分是建立预处理表，而得到此矩阵只需要进行8次数字2～9与大整数乘法运算，利用预处理表就直接找到试商结果。相对文献[7]中提出的算法，本文算法在乘法效率上优于前者，与文献[7]得出的性能表相比，体现了改进算法的优越性。故普通取模算法采用基于R进制模余数表的快速动态取模算法[15]，在和改进的取模算法进行比较之后，每种位数使用10组不同的大整数进行实验，得到程序整体运行的平均时间实验数据表如表4所示。

表4 算法运行位数-时间表

表4显示普通算法和改进算法的运行时间随位数变化的数据，可以看出随着位数的不断增大，普通算法的运行时间增长很快，从100位时的0.009 0 s增长到3 000位时的11.468 3 s，而改进后算法的运行时间增长缓慢，从100位时的0.000 9 s增长到3 000位时的0.021 9 s，充分说明改进后的算法效率提升得很明显。

图1和图2分别表示普通算法和改进算法的运行时间随位数变化的趋势，可以看出随着位数的不断增大，普通算法的运行时间是以109ns级的速度增长，原因是随着位数的增大，在每次试除时要进行多次因式分解，使得算法的开销增大，当位数增长到3 000位时，算法的效率已经无法容忍；改进的大整数取模算法运行时间是以107ns级的速度增长，通过访问查询矩阵得到试商结果，减少大量的算法开销，即使位数增长到3 000位时，算法的效率也很高。显然，在对大整数的取模运算中，通过实验数据证明了根据分治法思想提出的大整数取模快速算法的合理性和高效性。

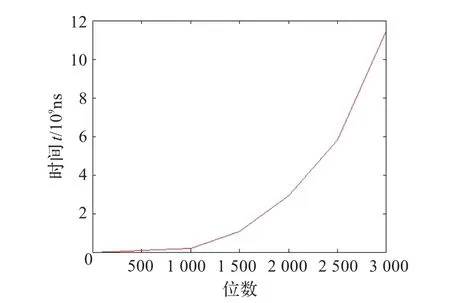
图1 普通算法的位数-时间图

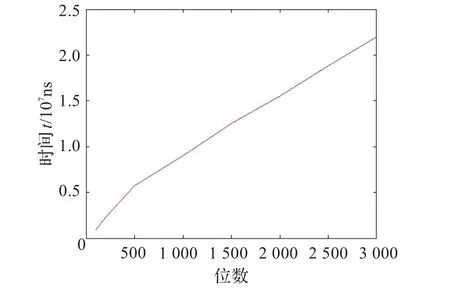
图2 改进算法的位数-时间图

4 结束语

通过对大整数取模运算的理论研究和实验分析，本文采用分治法的思想，建立预处理表，有效地将时间复杂度降为O(n(m-n))。研究结果和程序实验数据表明了改进算法在大数取模运算时的高效性和合理性，并随着n的不断增大，效率提升越明显。但在大整数取模运算中，由于大数比较和减法是传统的按位运算，使得改进算法整体效率有所降低，将在以后的研究中采用滑动窗口方式提高大数比较和减法效率。综上所述，本文以空间换取时间，采用分治法策略，提高了大整数取模运算在实际应用中的效率，对公钥密码学算法的研究具有重要意义。

[1]Rivist R，Shamir A，Adleman L M.A method for obtaining digital signatures and public-key cryptosystems[J].Communications of the ACM，1978，21（2）：120-126.

[2]Diffie W，Hellman M E.New direction in cryptography[J]. IEEE Transactions on Information Theory，1976，22（6）：644-654.

[3]Montgomery P L.Modular multiplication without trial division[J].Mathematics of Computation，1985，44（170）：519-521.

[4]陈恭亮.信息安全数学基础[M].北京：清华大学出版社，2004：1-29.

[5]王晓东.计算机算法设计与分析[M].2版.北京：清华大学出版社，2008：19-30.

[6]Chen Junhong，Wu Hao-Hsuan，Lin Wen-Ching，et al.A new modular exponentiation architecture for efficient design of RSA cryptosystem[J].IEEE Transactions on Information Theory，2008，16（9）：1151-1161.

[7]王岩，周亮，王远奎，等.大整数模运算的软件实现方案[J].信息安全与通信保密，2005，26（2）：150-151.

[8]Koç C K，Kaliski B S.Analyzing and comparing montgomery multiplication algorithms[J].IEEE Micro，1996，16（3）：26-33.

[9]赵学秘，陆洪毅，戴葵，等.一种高性能大数模幂协处理器SEA[J].计算机研究与发展，2005，42（6）：924-929.

[10]刘强，佟冬，程旭.一款RSA模乘幂运算器的设计与实现[J].电子学报，2005，33（5）：923-927.

[11]王远奎.大整数快速模运算算法与实现研究[D].成都：电子科技大学，2003.

[12]童元满.高性能公钥密码协处理器的设计与实现[D].长沙：国防科学技术大学，2004.

[13]周健，李顺东，薛丹.改进的大整数相乘快速算法[J].计算机工程，2012，38（16）：121-123.

[14]Eckel B.Java编程思想[M].陈昊鹏，译.4版.北京：机械工业出版社，2007：209-300.

[15]章昭辉，王晓蒲，霍剑青.公钥密码体制中快速模算法的研究[J].计算机工程与应用，2002，38（8）：56-58.

XU Xin,LI Shundong

School of Computer Science,Shaanxi Normal University,Xi’an 710062,China

Modular operation is a basic operation in modern cryptography.It plays an important role in public key cryptography based on factorization assumption.This paper proposes a fast modular operation algorithm for them-bit andn-bit integers.This algorithm,utilizing divide and conquer thought,transfers modular operation into subtractions,and then establishes a preprocessing table to further reduce the computational complexity toO(n(m-n)).Experiments show that this algorithm outperforms existing algorithms.

modular operation;cryptography;preprocessing table;divide and conquer;computational complexity

大整数取模运算是密码学应用的一种基本运算，尤其是在基于因子分解假设的公钥密码学中占有极其重要的地位。提出的m位和n位两个大整数快速取模算法，是利用分治法思想，将n位的大整数分解为n个独立十进制整数的组合，通过八次大整数乘法建立一个预处理表，能够有效地将大整数取模的计算复杂度降为O(n(m-n))，经大量实验数据验证该算法的合理性和高效性。

大整数取模；密码学；预处理表；分治法；计算复杂度

A

TP301

10.3778/j.issn.1002-8331.1212-0149

XU Xin,LI Shundong.Fast algorithm for modular operation.Computer Engineering and Applications,2014,50（22）：136-140.

国家自然科学基金（No.61070189，No.61272435）。

许鑫，男，硕士研究生，主要研究方向：信息安全，密码学。E-mail：xuxinshr@vip.qq.com

2012-12-13

2013-03-11

1002-8331（2014）22-0136-05

CNKI网络优先出版：2013-03-29，http://www.cnki.net/kcms/detail/11.2127.TP.20130329.1540.009.html

◎数据库、数据挖掘、机器学习◎