基于颜色Petri网的不确定库存模型性能仿真

郑文艳

德州学院信息管理学院，山东德州 253023

基于颜色Petri网的不确定库存模型性能仿真

郑文艳

德州学院信息管理学院，山东德州 253023

1 引言

分散型供应链是基于局部信息的，并且具有这样的特点，在供应链的参与者之间缺少协调，所做出的决策经常和不同类型的订货策略即向上游节点订货的数量相关联。而供应链管理的主要目标是整合供应链中上下游之间的产品和信息流以避免库存数量的过度波动。因此，对供应链中的参与者来说产品和信息是必须要考虑的方面。仿真工具为供应链的分析和验证提供了一种有效的方法。

Lionel等[1]提出使用多目标优化算法与遗传算法相结合去优化供应链库存策略。实验表明所提出的库存策略方法比目前现有的方法在减少库存成本和提高服务水平方面有着更好的效果，但是最小化库存的总成本以及运输成本仍是需要研究的问题。曾强等[2]基于VB开发了实现(t,s,S)库存优化的软件，模拟结果符合实际，由于顾客的实际需求不都是整数随机分布，而可能是连续随机分布，因此，软件有待进一步研究与改进。王鹏飞[3]运用系统动力学方法建立了一对一的从制造商到终端客户的两极供应链库存控制模型，通过对其进行仿真分析和优化，提出了参数及结构优化策略，而本文并未涉及一对多及多对多的多级库存控制系统。Yang H C等[4]开发了一个虚拟生产控制系统，该系统位于制造商端，制造商根据短期需求计划去调整供应商的产品速度以便于降低库存水平，还可以远程监控供应商的生产进程。该系统尤其适合用户控制他们的外包生产。Makajić等[5]使用时间，分层的颜色Petri网建立了一个包括零售商、批发商和制造商的三级供应链模型，模拟并进行了诸如牛鞭效应，库存水平的实时变化等方面的性能分析。Papanagnou等[6]提出了分析供应链系统的模拟框架，使用颜色Petri网分析了三种不同的订货策略，由于供应链是复杂的动态系统，因此需要进一步考虑现实供应链的所有特征。

基于此，本文使用颜色Petri网结合不同的需求预测方法及(s,Q)库存策略，设计决策过程并用仿真结果展示供应链中各环节库存实时状态，库存补充，配送及缺货等各种现实系统中产生问题的主要部分，以及不同参数的设定与目标费用函数的关系，为供应链的模拟和未来的仿真工作提供了新思路。

2 基础知识

2.1 着色Petri网的定义

2.2 CPN的ML语言

在CPN Tools中使用CPN ML语言进行变量的声明和Petri网的描述及定义。此处仅介绍函数类型。

函数的声明语法：

其中exp1和exp2类型要相同。

3 供应链的CPN模型及其描述

3.1 供应链的功能描述

供应链有五个参与者，顾客（customer），零售商（retailer），批发商或供应商（supplier），分销商（distributor）和制造商（manufacturer）。每一个参与者根据自己的局部情况做出决策，基于预测技术并遵循某一订货策略向上游产生订货订单，向下游运输配送产品同样遵循特定的规则和条件。参与者在减少本身库存（对下游提交的订单产品进行配送）的情况下同时也在增加库存量（根据下游订单向上游提交新订单）以便维持本身库存水平。

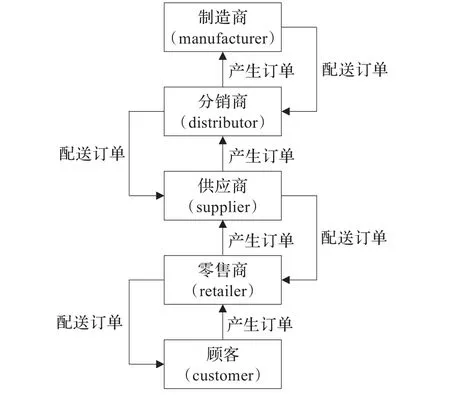
图1 供应链流程图

对每个参与者的几个主要活动描述如下，限于篇幅此处仅以图2所示的模型中retailer子页为例进行说明：

（1）订单的产生

分两种情况，一是终端顾客产生的初始订单；二是Retailer，supplier和distributor利用需求预测技术产生的订单：

①终端顾客的需求行为从两个方面进行限定，一是产生订单的数量，二是前后两次订单间隔的时间。形成的订单由三元组组成（订单号，订单产生的时间，订单数量）。这些参数的值是可以按照实际需求进行修改的，并且很容易检测当一个单一事件发生后对供应链中其他节点诸如库存水平等因素的影响。另外模型还允许其他类型的需求，比如季节性的浮动等均可以实现。

②根据下游提交的订单形成新订单即需求预测：由于配送下游订单的产品会减少库存量，为了保持库存水平，减少由于缺货造成的增加成本，参与者需要及时向上游订货以补充库存。Retailer，supplier和distributor新订单的数量均按以下两种方式之一进行预测：各个阶段加权平均值(MA)以及平滑指数分布(ES)[9-10]。而customer按照正态分布随机产生订单数量，manufacturer按固定量产生对原材料的需求。

（2）产品的配送

接收到订单时，需要检测当前库存量是否满足订单需求，如果库存显示有足够量的产品，那么订单产品被一次性配送；否则，如果库存量不足就有可能出现两种情况，一种情况等待库存量达到订单数量后再进行配送，另一种情况是进行不完全配送，库存量只要不为0就配送，直到订单产品全部完成配送。即一个订单的配送次数是多次的。本文CPN模型采取多次配送的方式。

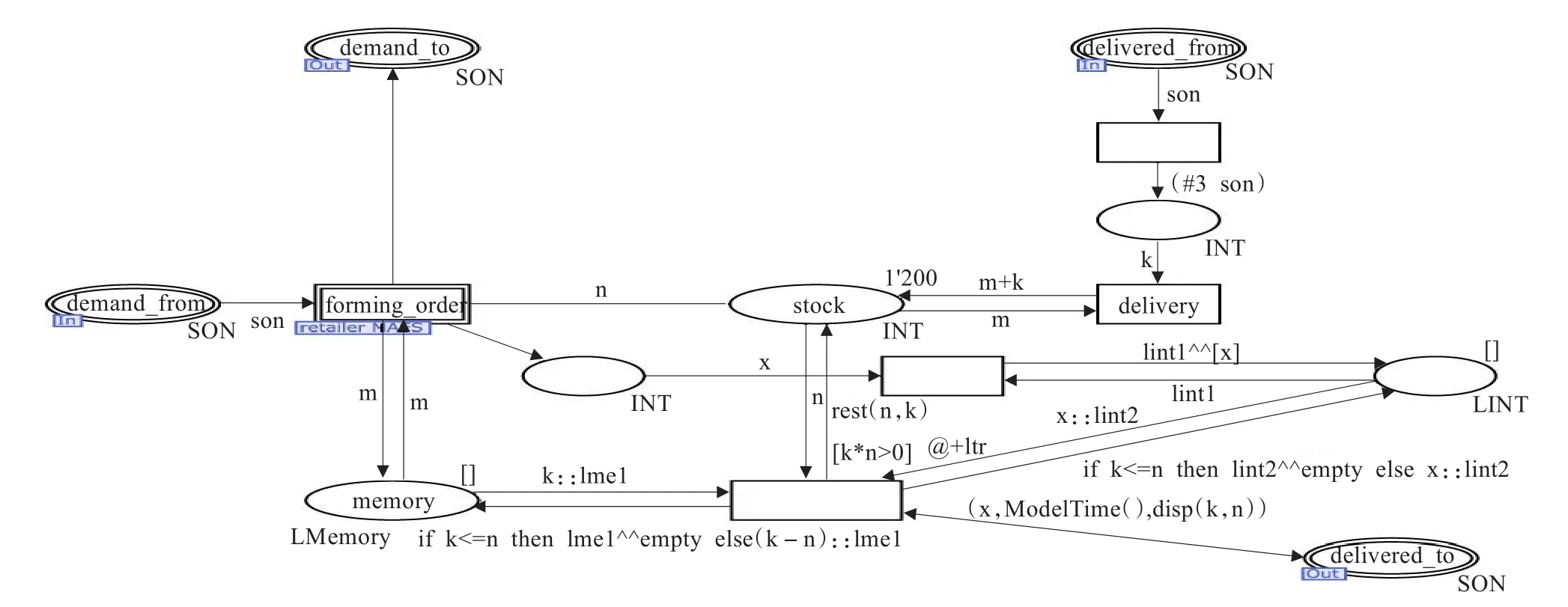
图2 retailer子页

（3）库存控制策略

为保障供应链的正常运行，除customer外每个参与者均需要按照库存控制策略保持自身的库存水平。Retailer，supplier和distributor采取的库存控制策略是根据上游提交订单产品的配送及时补充；而manufacturer采取了(s,Q)[11]的库存策略，当库存量低于订货点s时，及时补充固定量Q的原材料。

3.2 目标函数说明

在库存系统，涉及到订货费用（用CD表示），存储费用（用CP表示），缺货损失费用（用CS表示），目标实施总费用（用CT表示），计算公式表示如下[12-13]：

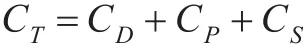
目标是使总费用CT最少。

具体说明如下：

（1）订货费用CD，包括两部分，一部分是每次订货必须支付的与订货量无关的手续费用，用K表示，发生的订货次数用s表示；一部分是每件货物需要支付的费用，用m表示，假定订货量为Z，则CD=K×s+m×Z。

（2）存储费用CP，是指维持库存所产生的费用，如果库存量为0，则不需要计算该部分存储费用。假定每件货物单位时间内存储费用为h，每件货物在仓库存储的时间为t，货物数量为n，则CP=h×t×n。

（3）缺货损失费用CS，是指供货方发生缺货行为时所产生的费用，假定每件货物的缺货损失费用为p，缺货货物数量为l，则CS=p×l。综上，得：CT=CD+CP+CS=K×s+m×Z+h×t×n+p×l。

3.3 功能函数说明只配送订单的一部分，配送数量为当前库存的数量，同时库存量更新为0。

（2）函数fun disp(i,j)=if i＞=j then j else i

函数功能描述：配送产品的数量。根据库存量j和等待配送订单队列中队首元素i判断配送数量，如果库存量j比等待配送的订单数量i多，则此次配送数量为订单数量i；否则，配送数量为当前的库存量j。

函数功能描述：该函数用于更新列表信息，模型中为保证顾客订单按产生的先后顺序进行配送，并且保证一个订单全部配送完后才开始配送下一个订单，在两个地方用到了该函数及列表，一个是等待配送的订单号，另一个是等待配送的订单数量。这样才能保证订单的正确配送。如果当前等待配送的订单数量k小于当前的库存量n，那么把该订单号从列表中移除，并把订单数量从等待配送的列表中移除；否则，如果库存量不足以完成一次配送，那么订单号继续留在列表的表头，同时更新配送列表中表头的数量为k-n。这样从订单顺序和订单数量两方面保证了配送的正确进行。

3.4 随机变量

功能函数均使用ML语言实现：

（1）函数fun rest(i,j)=if(i＞=j)then i-j else 0

函数功能描述：根据接收的下游订单数量j和自身的库存量i去更新库存，如果库存量i大于等于订单数量j，那么将对订单进行配送，库存量更新为i-j，否则

假设模型没有信息交换和信息处理的延迟，即信息交换和处理是及时的，是不消耗时间的。整个模型中只有产品的配送运输是要消耗时间的。

本模型涉及以下几个随机变量：

（1）顾客需求量随机变量：即顾客产生的订单数量，服从均值μ=100.0标准偏差σ2=8.0的正态分布，其概率密度函数为：

（3）货物配送延迟时间随机变量，指从订货到货物入库所需要的时间，根据统计数据，各阶段的订单配送延迟时间服从[1.4,4.2]之间的均匀分布，其分布函数为：

4 模型仿真及性能分析

模型模拟仿真1 500步，耗时51个时间单位。现从以下几个方面展示实验结果。

（1）采取MA或ES需求预测技术前后的对比图

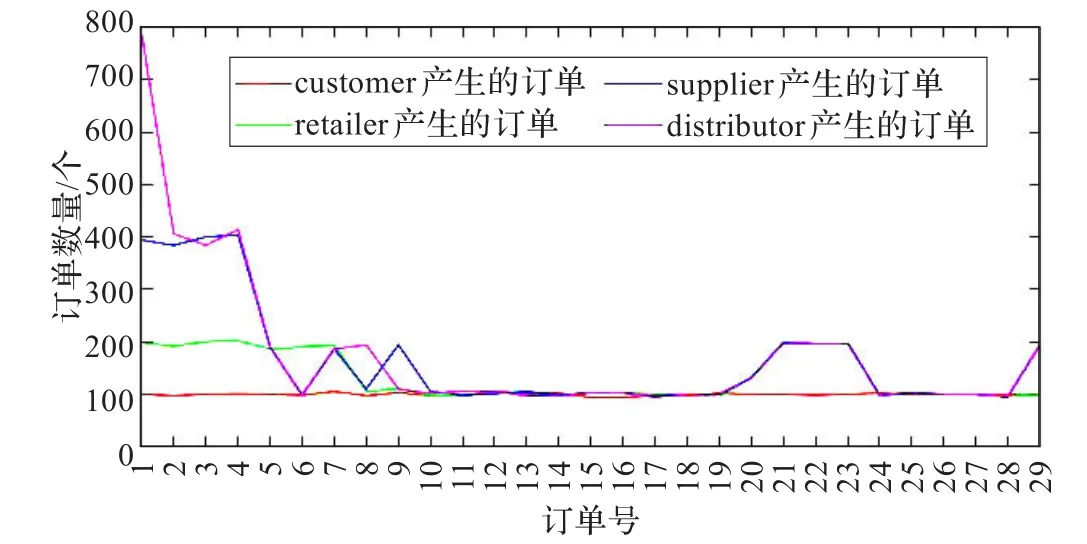
图3 未采取预测策略的牛鞭效应图

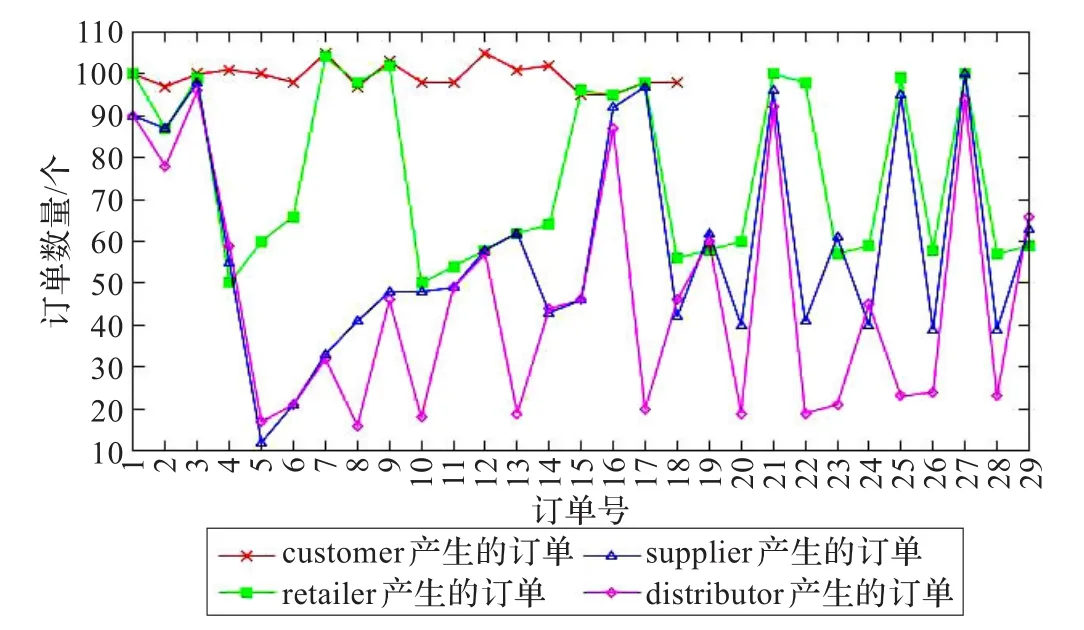
图4 采取MA或ES预测技术后参与者产生订单数量的分布图

同样的顾客需求条件下，没有采取任何策略而产生的牛鞭效应[14-15]图如图3所示，而采取了MA或ES策略后订单向上游传递的信息如图4所示。从前后的对比分析图可以看出，牛鞭效应最高可达到8倍，并且整个波动幅度比较大且频繁。而采取了需求预测技术之后，消除了牛鞭效应，需求预测量在逐渐降低。以参与者之一Retailer为例，进一步展示修改前后对比图如图5所示。随着订单向上游的传递，修改前后的差距在逐渐减小。

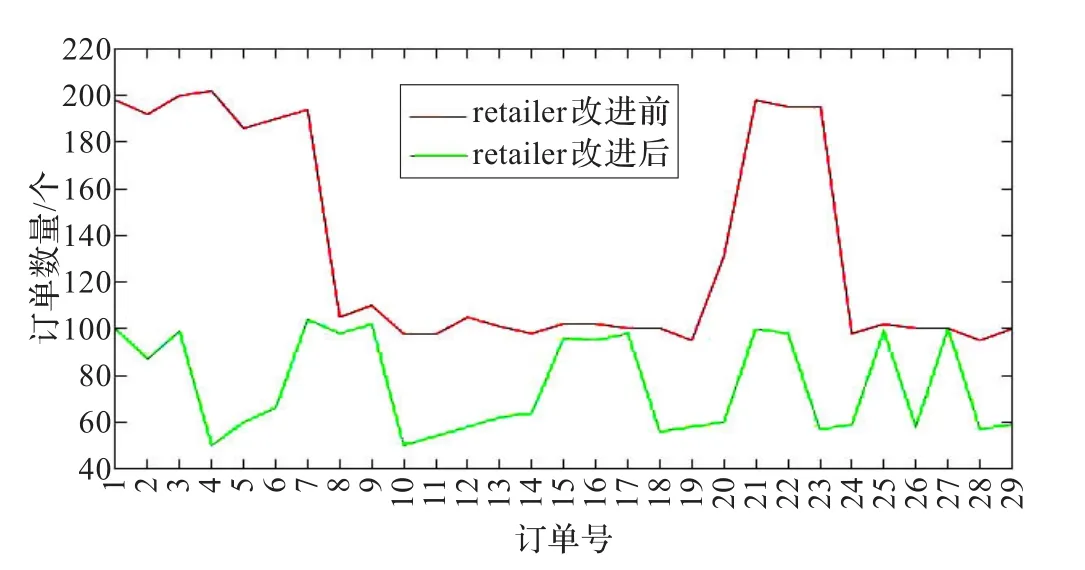
图5 retailer采用预测技术前后产生的订单数量对比图

（2）各参与者从订单接收、配送以及库存缺货状态三方面的分析对比图

以retailer为例展示从接收的下游订单，对下游订单的配送以及库存缺货三个方面做详细分析，如图6和图7所示。图中x轴表示订单号，从每个订单号可以看出该订单配送的情况以及库存缺货的情况。订单号1至6均未发生库存缺货的情况，并且订单的配送均是一次性完成，订单号7虽然也没有缺货，但是订单的配送是分2次完成的。订单号8至17均不同程度上发生了缺货，并且订单配送是分多次完成的。库存缺货和订单配送次数是密切相关的，如果库存未缺货但订单却多次配送，说明库存补充是及时的。如果库存补充及时，订单配送虽然多次完成，但缺货状态会减少，因为库存补充是降低缺货发生的关键因素。

图6 retailer订单接收、配送及库存缺货情况分布图

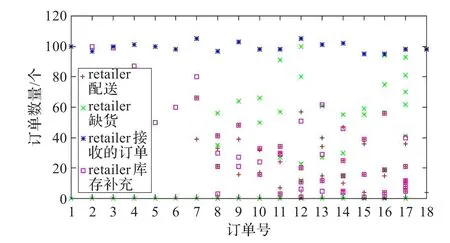
图7 retailer订单接收配送及库存缺货及库存补充情况分布图

（3）初始库存量与存储费用，订货费用及缺货延迟费用的对比分析图

根据模型初始假定得知下游顾客提交的订单数量在[94，106]之间，向上游提交的订单数量在[37，106]之间，库存补充时间延迟在[0，3]之间。根据目标实施总费用CT的计算公式：CT=CD+CP+CS=K×s+m×Z+h×t×n+p×l得知总费用以及需求预测与初始库存的关系。

根据顾客提交的订单数量范围，选取五种初始库存数量，50，100，200，300和500。图8中x轴几个坐标代表的含义分别为：（1）采取ES的需求预测方法；（2）采取MA的需求预测方法；（3）存储费用；（4）缺货延迟费用。

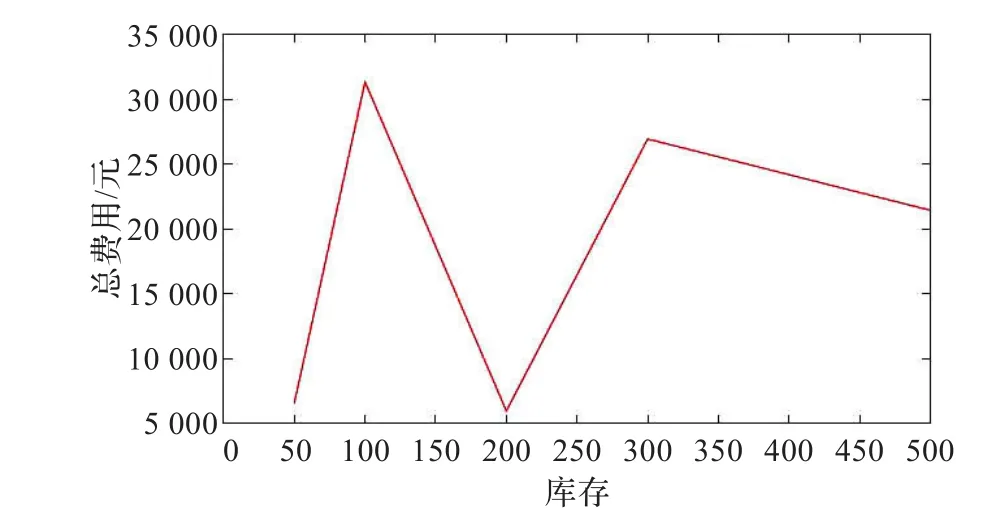
图8 初始库存分别为50，100，200，300，500时产生的总费用情况

从图9可以看出如果要使总费用最低：

①存货费用与初始库存的关系并不严格成递增或递减关系，而为下游提交订单数量的2倍左右为最佳。

②ES和MA两种需求预测方法相对来说MA这种方式产生的订货费用要少一些。

③存储费用与库存量的关系基本符合正比关系；在200处为最低。

④缺货延迟费用最低的为200，如果库存比200大，则两者关系成反比，反之两者关系成正比关系。

图9 不同初始库存量订货费用、存储费用及缺货延迟费用分析对比图

综上，该模型直观显示了初始库存量与订货费用，存货费用以及延迟费用之间的关系，并且通过修改变量很容易变更订单数量，前后订单间隔时间，货物配送延迟时间等，从而在各种因素间找出使得总费用最低的最优库存管理策略。

（4）不同(s,Q)库存策略与初始库存，存储费用，订货费用及缺货延迟费用的对比分析图

①初始库存与总费用及各项费用的关系

表1 (s,Q)固定情况下初始库存与费用关系表元

下游提交的订单数量在[10，106]之间，(s,Q)=(80,100)的情况下，订货费用最低的是初始库存为100，存储费用和缺货费用最低均出现在初始库存为0，而总费用最低也出现在初始库存为0时。

②初始库存为0时，订货点s与费用的关系

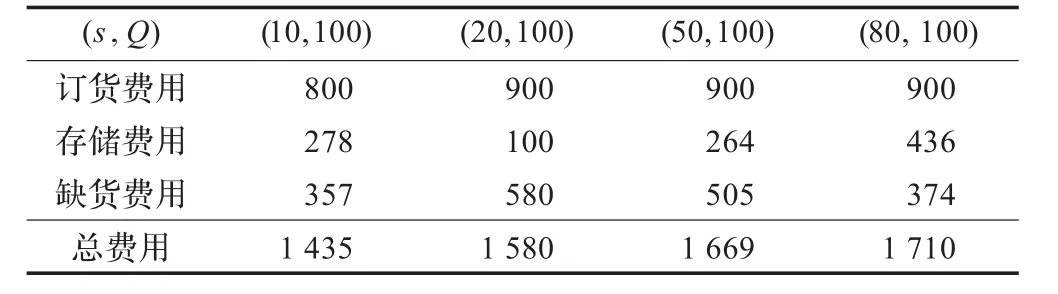
表2 初始库存为0时订货点s与费用的关系表元

订货费用不变，存储费用随着订货点的增加而增大，缺货费用与订货点成反比关系，总费用与订货点成正比关系，因此如果要使目标函数最小，则订货点也应该越小。

③初始库存为0时，订货点s=20时固定订货量Q与费用的关系

表3 初始库存为0，订货点s=20时固定订货量Q与费用的关系表元

订货点固定时，如果固定订货量比下游订单的上界数量大，那么存储费用及订货费用与Q成正比，而缺货费用与Q成反比，当Q足够大时缺货费用为0，如果Q比较小，缺货费用的增长幅度是比较大的。因此如果要使目标函数最小，则固定订货量Q不能小于订货点s，并且也应该越小越好。

5 结论

本文以颜色Petri网为工具，构造了不同需求预测技术及库存控制策略的CPN模型，在初始库存量，订货点及订货量等参数未知情况下，通过实验仿真数据，清晰准确地实现了使目标函数最小的最优库存管理策略。

[1]Amodeo L，Chen H，El Hadji A.Supply chain inventory optimisation with multiple objectives：an industrial case study[M]//Advances in computational intelligence in transport，logistics，and supply chain management.Berlin Heidelberg：Springer，2008：211-230.

[2]曾强，潘启东，沈玲.(t,s,S)库存系统的计算机优化仿真[J].工业工程，2007（3）：123-127.

[3]王鹏飞.基于系统动力学的产销两级供应链库存控制仿真研究[D].重庆：重庆大学，2010.

[4]Yang H C，Chen Y L，Hung M H，et al.Virtual production control system[C]//2010 IEEE Conference on Automation Science and Engineering（CASE）.IEEE，2010：984-989.

[5]Makajić-Nikolić D，Panić B，Vujošević M.Bullwhip effect and supply chain modelling and analysis using CPN tools[C]// Proceedings of the Fifth Workshop and Tutorial on Practical Use of Coloured Petri Nets and the CPN Tools，Aarhus， 2004：219-234.

[6]Papanagnou C I，Halikias G D.Analysing different ordering Policies in a series supply chain by using Coloured Petri Nets[C]//Proceedings of the 20th European Conference on Modelling and Simulation，2006：28-31.

[7]郑文艳.基于CPN的物流配送系统模型正确性的证明[J].计算机工程与应用，2013，49（11）：228-231.

[8]郑文艳.分层有色Petri网在物流配送系统仿真建模中的应用[J].计算机系统应用，2013（4）：164-168.

[9]Chen F，Ryan J K，Simchi-Levi D.The impact of exponential smoothing forecasts on the bullwhip effect[J].Naval Research Logistics，2000，47（4）：269-286.

[10]Chen F，Drezner Z，Ryan J K，et al.Quantifying the bullwhip effect in a simple supply chain：The impact of forecasting，lead times，and information[J].Management Science，2000，46（3）：436-443.

[11]Caplin A S.The variability of aggregate demand with（S，s）inventory policies[J].Econometrica：Journal of the Econometric Society，1985：1395-1409.

[12]卢剑峰，聂铁铸.随机库存系统最优订货策略计算机模拟研究[J].计算机技术与发展，2013（6）：50-53.

[13]Brunner K，Cukierman A，Meltzer A H.Money and economic activity，inventories and business cycles[J].Journal of Monetary Economics，1983，11（3）：281-319.

[14]Papanagnou C，Halikias G D.A state-space approach for analysing the bullwhip effect in supply chains[J].Proceedings of ICTA，2005，5：79-84.

[15]Lee H L，Padmanabhan V，Whang S.Information distortion in a supply chain：the bullwhip effect[J].Management Science，2004，50（12_supplement）：1875-1886.

ZHENG Wenyan

College of Information Management,Dezhou University,Dezhou,Shandong 253023,China

Because of distorted information and poor product management often lead to uncertainty and to instability phenomena.This paper considers the case of the supply chain model using Timed Colored Petri nets and analyses the impact of various continuous inventory policies and known forecasting methods followed by supply chain participants.CPN tools are used for the design of decision-making processes and simulation results are presented to highlight the main issues arising in real systems and to provide insights for future work on modeling and simulation of supply chains.

supply chain;forecasting;inventory control;colored Petri nets

供应链中由于信息传递过程中出现的信息膨胀引起牛鞭效应造成各种成本的急剧增长，为使目标函数费用最小，基于颜色Petri网建立了不同需求预测方法及库存策略的CPN模型。在订单数量等变量随机产生以及订货点等因素不确定的情况下，通过实验仿真数据确定了存储、订货及缺货费用与各种不确定变量的关系，从而确定了最优的库存策略。通过对比实验证明了该方法的有效性及正确性。

供应链；需求预测；库存策略；颜色Petri网

A

TP391

10.3778/j.issn.1002-8331.1402-0200

ZHENG Wenyan.Performance simulation of uncertainty inventory based on colored petri nets.Computer Engineering and Applications,2014,50（22）：250-255.

德州市社会科学研究基地项目；2013年山东省自然科学基金计划（No.ZR2013GL001）；德州市软科学研究计划项目（No.（2013）德科软第43号）；2013年校级科技发展计划项目（No.311678）。

郑文艳（1980—），女，讲师，主要研究领域为Petri网应用。

2014-02-20

2014-04-22

1002-8331（2014）22-0250-06

CNKI网络优先出版：2014-07-11,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1402-0200.html