超维纳指数的若干结果*
2014-08-03许冬冬高炜
许冬冬, 高炜
(云南师范大学 信息学院,云南 昆明 650500)
在理论化学中,常用图模型来表示分子结构,用顶点来表示原子,边表示它们之间的化学键.而化学分子的特性常常用一些参数来衡量,比如PI指数、维纳指数、Randic指数等等[1-5].本文只考虑无向、简单、有限图.设G是一个图,它的顶点集合和边集分别用V(G)和E(G)来表示.文中所用符号和标记若没有特别说明则与文献[6]一致.
一个图的维纳指数W(G)是图中所有顶点对的距离之和:

其中d(u,v)表示顶点u和v在G中的距离.超维纳指数WW(G)作为一般维纳指数的推广,其定义如下:
有关超维纳指数的研究是近年来理论化学研究的热点[7-10].本文将研究线图和一些特殊图类的超维纳指数,给出若干结果.
1 线图的超维纳指数
定理1 设G是有n个顶点,m条边的连通图,且顶点vi的度为di.若G的直径Diam(G)≤2且G的任意一个导出子图都不同构于下面的F1、F2和F3.

图1 G的导出子图的禁图
设L(G)为G的线图,则有:

(1)
对一个直径不超过2的连通图,易知在导出子图不同构于F1、F2和F3的条件下,其线图的直径也不会超过2.从而有
结论证毕.
推论1 设G是一个有n个顶点的连通r正则图.若G的直径Diam(G)≤2且G的任意一个导出子图都不同构于图1中的F1、F2和F3.则有
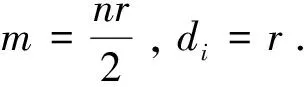
定理2 设G是一个连通图,其顶点集合V(G)={v1,v2,…,vn},边集合E(G)={e1,e2,…,em}.设vi的度为di.若e=uv是G的任意一条边,则e的度定义为d(e)=du+dv-2.则有
上式等号成立的充分必要条件为:G的直径Diam(G)≤2且G的任意一个导出子图都不同构于图1中的F1、F2和F3.
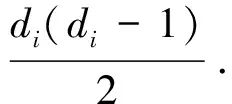
对于边e=uv,它一共关联了d(e)=du+dv-2条边.因此e在G中不关联的边共有m-1-d(e)条.在L(G)中,e与这m-1-d(e)个顶点的距离至少为2.从而有
若G的直径Diam(G)≤2且G的任意一个导出子图都不同构于图1中的F1、F2和F3,则Diam(L(G))≤2成立.e与这m-1-d(e)个顶点在L(G)中的距离恰好为2,从而
(2)
反过来要使(2)成立,那么G中任意两条不关联的边在L(G)中的距离必须为2.设ei和ej在L(G)中的距离为2,则存在G中的边ek同时与ei和ej关联.这时G的任意一个导出子图都不同构于图1中的3个禁图,且Diam(G)≤2.结论证毕.
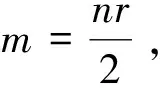
推论2 设G是一个有n个顶点的连通r正则图.则
上式等号成立的充分必要条件为:G的直径Diam(G)≤2且G的任意一个导出子图都不同构于图1中的F1、F2和F3.
下面两个定理讨论树的线图的超维纳指数计算公式.
定理3 设T是一个树,V(T)={v1,…,vn}且vi的度记为di(i=1,2,…,n).L(T)表示T的线图,则
证明线图L(T)的顶点即为原图T的边.对于每个顶点vi而言,有di条边和它相关联,这些边在L(T)中构成顶点数为di的完全图.因此这di个顶点之间的距离和以及距离平方和均为
(3)
设vi、vj是T中的顶点,它们的度分别为di、dj.设x1、x2、…、xdi-1是顶点vi在T中所关联的边,y1、y2、…、ydj-1是顶点vj在T中所关联的边,且满足xl和yk没有公共顶点(1≤l≤di-1,1≤k≤dj-1), 同时这些边都不在vi、vj之间的路径上.由此可知xl和yk在L(T)中的距离为1+d(vi,vj).从而关联vi的边x1、x2、…、xdi-1和关联vj的边y1、y2、…、ydj-1之间的距离和以及距离平方和分别为:
[1+d(vi,vj)](di-1)(dj-1)
(4)
[1+d(vi,vj)]2(di-1)(dj-1)
(5)
结合(3)-(5),可知
结论证毕.
定理4 设T是一个树,有k个度为s的顶点,其他顶点度均为1.T′是在T中删除所有终端顶点后得到的树.则
证明对于i=1,2,…,k, 设vi的度为s;而对于i=k+1,k+2,…,n,记vi的度为1.从而对于i,j=k+1,k+2,…,n,有di-1=dj-1=0.根据定理3的结果,可得
结论证毕.
2 若干图类的超维纳指数
定理5 设G是有n个顶点的连通图,并包含团Kk.设G(n,k)为在G中删除Kk的边得到的图,0≤k≤n-1.则有
等式成立当且仅当G≅Kn.
证明设V(G)={v1,v2,…,vn}.不失一般性,设团Kk的顶点集为S1={v1,v2,…,vk},G中剩下的顶点为{vk+1,vk+2,…,vn}.从而S1中任意两个顶点在G(n,k)中的距离至少为2,剩余顶点对在G(n,k)中的距离至少为1.得到
若G≅Kn,则可直接验证上式等号成立.

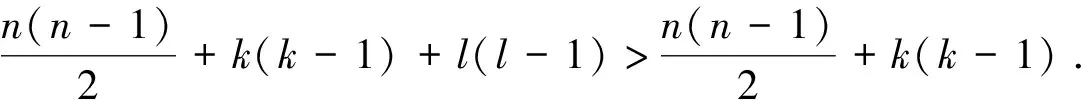
设G1、G2是G的两个子图.若|V(G1)∩V(G2)|=0成立,则称G1、G2是独立的.


结论证毕.
定理7 设ei(其中i=1,2,…,k,0≤k≤n-2)是完全图Kn中与某个顶点v相关联的k条边.设Kn(k)是从Kn中删除边ei(i=1,2,…,k)得到的图.则有

结论证毕.
参 考 文 献:
[1] YAN L,LI Y,GAO W,et al.PI index for some special graphs[J].Journal of Chemical and Pharmaceutical Research,2013,5(11):260-264.
[2] GAO W,SHI L.Wiener index of gear fan graph and gear wheel graph[J].Asian Journal of Chemistry,2014,26(11):3397-3400.
[3] GAO Y,LIANG L,GAO W.Eccentric connectivity index of some special molecular graphs and theirr-corona graphs[J].International Journal of Chemical and Process Engineering Research,2014,1(5):43-50.
[4] GAO Y,LIANG L,GAO W.Randic index and edge eccentric connectivity index of certain special molecular graphs[J].International Journal of Chemistry and Materials Research,2014,2(8):81-87.
[5] XI W,GAO W.Geometric-arithmetic index and Zagreb indices of certain special molecular graphs[J].Journal of Advances in Chemistry,2014,10(2):2254-2261.
[6] BONDY J A,MURTY U S R.Graph theory with applications[M].London:Macmillan Press,1976.
[7] YAN L,LI Y,GAO W,et al.On the extremal hyper-wiener index of graphs[J].Journal of Chemical and Pharmaceutical Research,2014,6(3):477-481.
[8] DOU J,WANG Y,GAO W.Some characteristics on hyper-wiener index of graphs[J].Journal of Chemical and Pharmaceutical Research,2014,6(5):1659-1663.
[9] PAN Y.Wiener number and hyper-wiener number of two types of polyomino systems[J].Journal of Mathematical Study,2013,46(3):260-269.
[10]CASH G.Three methods for calculation of the hyper-wiener index of molecular graphs[J].Journal of Chemical Information and Computer Science,2002,42,571-576.
