一些整函数的迭代性质与3n+1问题之间的关系*
2014-08-03李玉华
李玉华
(云南师范大学 数学学院,云南 昆明 650500)
1 引言及主要结果
T(n)即是人们通常所说的3n+1函数,它是一个极其简单的数论函数.
设X为一个非空集合,h:X→X为X上的自映照.对于任意的非负整数n,用符号h°n表示h的n次迭代,它们中的每一个也都是X上的自映照.对于任意的x0∈X,将点列h°n(x0) (n=0,1,2,…)称为x0关于h的(正向)轨道.如果对于某个y∈X,存在正整数ky,使得
h°ky(y)=y,h°j(y)≠y(∀j∈{1,2,3,…,ky-1}),
那么,称y为h的长度为ky的周期点.
3n+1函数看似简单,但是对其通过任意次迭代所产生的迭代函数列的混乱与复杂程度却远远超过大多数人的想象.Collatz L于1952年提出了如下猜想:
3n+1猜想[1]对于∀m∈,相应∃km∈,使得T°km(m)=1.
3n+1猜想亦称为3n+1问题,它的称述十分简单,知道整数的乘、除法的人都可以理解,但要解决它却极其困难,它目前仍是数论中的一个未彻底解决的问题.
设h(z)为超越整函数,由h(z)迭代所产生的整函数族{h°n(z)|n=0,1,2,…}的正规点所成之集合称为h(z)的Fatou集或稳定点集,用符号F(h)表示之,而F(h)相对于复平面的余集称为h(z)的Julia集或不稳定点集,简记为J(h).由解析函数的正规族定义(参见[2])可知:F(h)是的开子集.F(h)的每一个最大连通开子区域称为F(h)的一个分支.关于复解析动力系统更详细的内容可参见文献[3-4].
1996年,Chamberland M[5]将3n+1猜想与实解析动力系统的研究联系起来,为3n+1猜想的研究开辟了一条新的途径.1999年,Letherman S等[6]又进一步将3n+1猜想与复解析动力系统的研究联系起来,沿着这一思路继续深入探索,我们得到3n+1猜想在复解析动力系统中的如下等价形式.
定理1 设h(z)为超越整函数,h在自然数集Ν上的限制恰好为3n+1函数T,而且|h′(1)h′(2)|<1,并对于∀n∈Ν{1,2}有|h′(n)|≥2.则3n+1猜想成立的充分必要条件是:Ν⊂F(h).
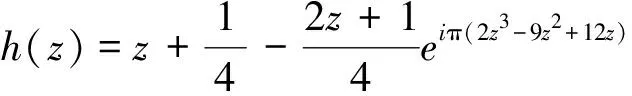
从复解析动力系统的观点来看,下述结果给出了一个关于3n+1函数的性态较好的插值整函数.
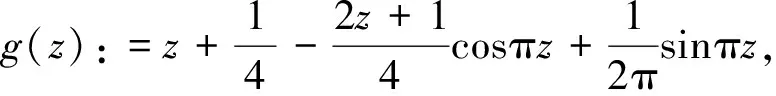
(1)g(z)在自然数集Ν上的限制是函数T;
(2)g(z)的临界点至多除有限个外都位于实轴上;
(3)F(g)的分支都是单连通的.
注意到定理2中的整函数g(z)限制在实轴上是一个实轴上的自映照,而在一维实动力系统的研究中,Schwartz导数为负的函数的动力学性质较好研究,那么g(z)作为实轴上的自映照,它的Schwartz导数会有什么样的性质呢?关于这个问题,我们有如下结果:

2 几个引理
在定理证明之前,先介绍几个辅助结果.
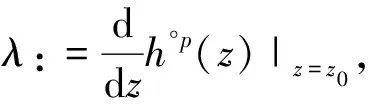
引理2[4]设h(z)为超越整函数,则对于∀n∈,有F(h°n)=F(h),J(h°n)=J(h).
引理3[7](Marty正规定则) 设F*为复数域的子区域D上的某些解析函数所成之族,则F*在D内正规的充分必要条件是:对于D的任意有界闭子区域D1,相应存在正数M,使得对于任意g∈F*以及任意z∈D1都有|g′(z)|≤M·(1+|g(z)|2).
引理4[3]设h(z)为超越整函数.如果存在正数A和K以及延伸到∞的简单曲线Γ,使得|h(z)|≤A|z|K(∀z∈Γ),则F(h)的分支都是单连通的.
3 定理的证明
3.1 定理1的证明
由于h(1)=2,h(2)=1,而|(h°2)′(1)|=|(h°2)′(2)|=|h′(1)h′(2)|<1,所以由引理1可知:
{1,2}⊂F(h)
(1)
如果3n+1猜想成立,则对于∀k∈,均相应存在nk∈,使得
h°nk(k)=T°nk(k)=1
(2)
由式(1)、(2)和引理2可得:Ν⊂F(h),定理必要性得证.
如果Ν⊂F(h),则我们断言3n+1猜想成立.事实上,如若不然的话,那么必然存在k0∈Ν,使得有
h°j(k0)=T°j(k0)>2,(∀j∈)
(3)
又利用数学归纳法容易得到

(4)
由(3)和已知条件得
|(h°j)′(k0)|≥2j,(∀j∈)
(5)
(6)
由(6)和引理3可知:整函数族{h°j(z)|j=1,2,3,…}在点k0处必定不正规,从而有k0∉F(h),这与Ν⊂F(h)相矛盾,定理充分性得证.所以上述断言成立.定理1证毕.
3.2 定理2的证明
结论(1)显然成立.兹开始证明结论(2).容易求得
(7)
(8)
由(7)式知道方程g′(z)=0等价于
(9)

wcosw=2
(10)
易见,要证明方程(9)除至多有限个根外其余的根均位于实轴上,只需证明方程(10)除至多有限个根外其余的根均位于实轴上.
继令w=u+iv(其中u与v均为实变量),则方程(10)转变为下面关于u与u的方程:
(u+iv){(ev+e-v)cosu+(e-v-ev)sinu}=4
(11)
通过分离实部与虚部,方程(11)转化为下述方程组:
(12)
由于映照φ(w):=wcosw-2保持实轴不变,因而它的零点集的分布关于实轴对称,鉴于这一原因,设w0=u0+iv0(u0≠0,v0>0)是方程(10)的根,则有
(13)
由于u0≠0,v0>0,从而由(13)得cosu0·sinu0≠0,而且有
(14)
另一方面,对w0cosw0=2两边取摸的平方后整理得
(15)
由(15)知道|u0|+|v0|→+∞必然导致u0→∞,v0→0+,而且|sinu0|→1.由此可知当|w0|充分大时,(14)中第二个式左边的绝对值严格大于右边的绝对值.这就说明存在正数M0,使得方程(10)的位于{w∈||w|>M0}内的根全部落在实轴上的集合(-∞,-M0)∪(M0,+∞)之中.由此可知g(z)的临界点至多除有限个外都位于实轴上.
最后证明结论(3).由于对于任意不小于4的实数z有|g(z)|≤2|z|,从而由引理4知F(g)的分支都是单连通的.定理2证毕.
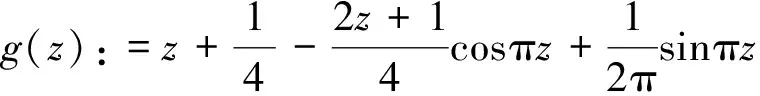
3.3 定理3的证明
由(8)式得

(16)
由(7)、(8)和(16)诸式得

-12sin2πz-2π2(2z+1)2cos2πz-π2(2z+1)2}
(17)
注意到,对于任意的实数z有-1≤sinz≤1,-1≤cosz≤1,由此和(17)知:存在M>0,使得2g‴(z)g′(z)-3(g″(z))2<0(∀z∈(-∞,-M)∪(M,+∞)).由此即可推出所期望的结论.定理3证毕.
从定理3的证明过程中可以看出,进一步讨论即可得出M的值.
参 考 文 献:
[1] LAGARIAS J C.The 3x+1 problem and its generalizations[J].Amer.Math.Monthly,1985,92(1),3-23.
[2] YANG L.Value distribution theory[M].Berlin Heidelberg:Springer-Verlag,Beijing:Science Press,1993.
[3] 任福尧.复解析动力系统[M].上海:复旦大学出版社,1997.
[4] 吕以辇.复解析动力系统[M].北京:科学出版社,1995.
[5] CHAMBERLAND M.A continuous extension of the 3x+1 problem to the realine[J].Dynam.Contin.Discrete Imluls.System,1996,2(4):495-509.
[6] LETHERMAN S,SCHLEICHER D,WOOD R.The 3n+1-problem and holomorphic dynamics[J].Experimental Mathematics,1999,8(3):241-251.
[7] 顾永兴.亚纯函数的正规族[M].成都:四川教育出版社,1988.
