Klein-Gordon-Schrödinger方程组的精确解*

何猛, 王跃

(昆明冶金高等专科学校,云南 昆明 650031)

1 引 言

(1)

为Klein-Gordon-Schrödinger方程组[1]，该方程组是描述一个守恒的复杂核子场和中性的真实介子场进行Yukawa相互作用的经典数学模型[2-3].其中u:R×R3→C是一个复数域上的核子运动，v:R×R3→R是实数域上的介子作用，正常数m是介子的质量[4].应用动力系统理论方法，李继彬研究了Klein-Gordon-Schrödinger方程组的孤立波和周期行波解，给出了解存在的明显参数条件以及孤立波和周期行波解的表达式[5].本文使用包络变换和直接拟设法探求Klein-Gordon-Schrödinger方程组的孤立波解，求出的亮孤立波解和暗孤立波解是以往研究中均未得到的.

2 包络变换和直接拟设法求解

假设方程组(1)具有行波解：

u=P(ξ)ei(kx+ϖ t+φ(ξ)),v=Q(ξ)

(2)

其中P(ξ)、Q(ξ)、φ(ξ)均为实函数.

将(2)代入(1),并分别令实部和虚部为零，得如下方程组：

(3)

利用上述方程组，下面分别探求方程组(1)的亮孤立波和暗孤立波.

2.1 亮孤立波解

假设方程(3)有如下形式的亮孤立波解：

(4)

将(4)分别代入(3)，得如下方程组：

(5)

令方程组(5)tanhiξ(i=0,1,2)的系数为零，得系数方程组：

(6)

利用数学软件Maple求解，可得如下两组解:

情形1.

(7)

此时，(7)为方程组(1)的亮孤立波解.

情形2.

(8)

可知，(8)也是方程组(1)亮孤立波解.

2.2 暗孤立波解

假设方程(3)有如下形式的暗孤立波解：

(9)

将(9)分别代入(3)，可得如下方程组：

(10)

令方程组(10)中的tanhiξ(i=0,1,2)的系数为零，得系数方程组：

(11)

利用数学软件Maple求解，可得如两组下解:

情形3.

(12)

此即是方程组(1)的暗孤立波解.

情形4.

(13)

则(13)为方程组(1)的另一暗孤立波解.

2.3 数值模拟图

选取适当数据，给出系统(1)的亮孤立波解和暗孤立波解的数值模拟：

情形1 取m=2,k1=1,此时，亮孤立波解(7)为：

(14)

解(14)图像如图1、图2所示:

图1 亮孤立波解|u|2的图像 图2 孤立波解v的图像

情形2 取m=2,k1=1,此时，亮孤立波解(8)为：

(15)

则解(15)图像如图3、图4所示:

图3 亮孤立波解的图像 图4 孤立波解v的图像

情形3 取m=2,k1=1,此时，暗孤立波解(12)为：

(16)

此时，解(16)的图像如图5、图6所示：

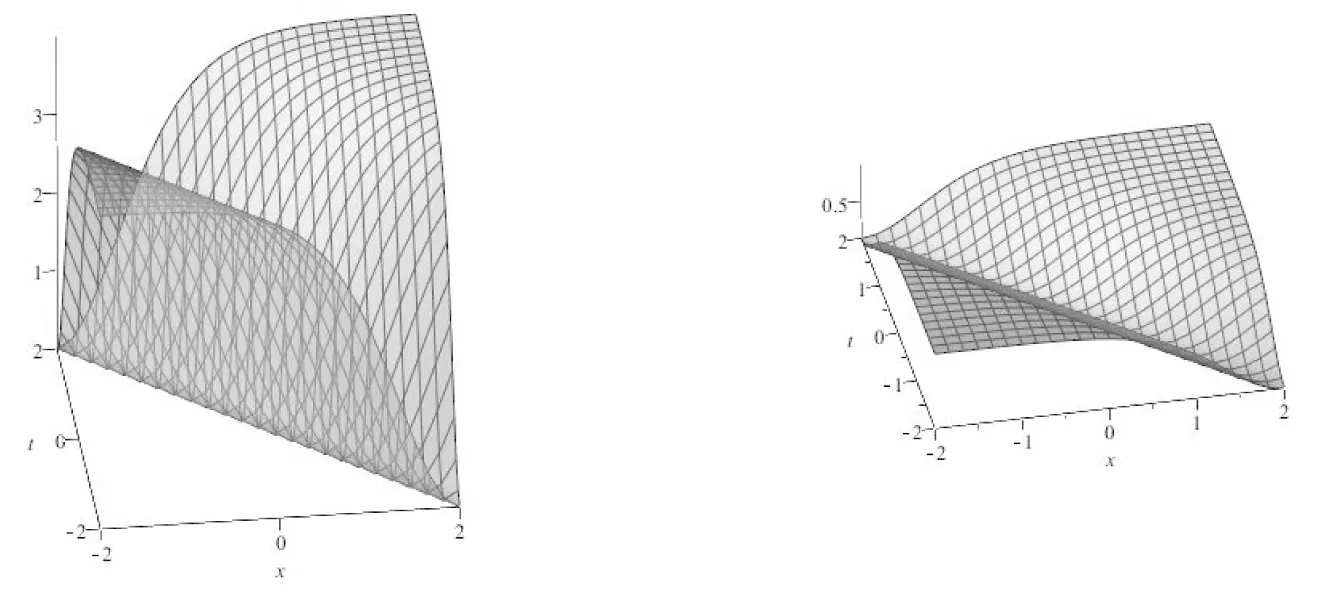
图5 暗孤立波解|u|2的图像 图6 孤立波解v的图像

情形4 取m=2,k1=1,此时，暗孤立波解(13)为：

(17)

此时，解(17)的图像如图7、图8所示：

图7 暗孤立波解|u|2的图像 图8 孤立波解v的图像

3 结 论

本文用包络变换和直接拟设法求得Klein-Gordon-Schrödinger方程组的亮孤立波解和暗孤立波解，并对该方程组的解作出数值模拟.亮孤立波解和暗孤立波解在以往的研究文献中未曾得到，这对于进一步刻画该类方程(组)的非线性传播的动力学行为，有着重要的物理意义.

参 考 文 献:

[1] FUKUDA I,TSUTSUMI M.On coupled Klein-Gordon-Schrödinger equations II[J].J.Math.Anal.Appl.,1978,66(2):358-378.

[2] FAN E.Uniformly constructing a series of explicit exact solutions to nonlinear equations in mathematical physics[J].Chaos Solitons Fractals,2003,16(5):819-839.

[3] HE J H,WU X H.Construction of solitary solution and compacton-like solution by variational iteration method[J].Chaos Solitons Fractals,2006,29(1):108-113.

[4] YUKAWA H.On the interaction of elementary particles I[J].Proc.Physico-Math.Soc.Japan.,1935,17(2):48-57.

[5] LI J B.Solitary and periodic traveling wave solutions in Klein-Gordon-Schrödinger Equations[J].云南大学学报：自然科学版，2003，85(3)：176-180.