滤子Vs.格值滤子

张 辉,李令强,孟广武,汤建钢

(1.聊城大学数学科学学院,山东 聊城 252059;2.伊犁师范学院数学与统计学院,新疆 伊宁 835000)

1 预备知识

滤子是研究拓扑的基本工具之一[1]. 类似的,格值滤子在格值拓扑的研究中也起到了至关重要的作用. 近年来,以强化的预幺半群L作为基本格结构的格值(或者多值)拓扑理论以其与多值逻辑的密切联系而受到越来越多的关注[2-10]. 本文详细讨论了滤子与L-滤子之间的关系.这对研究拓扑与多值拓扑及其收敛之间的关系具有重要的意义.

称三元组(L,≤,*)为一个GL-幺半群,其中(L,≤)是一个完备格,1和0分别为其最大元和最小元,*是L上的二元运算满足如下性质[2,5]:

(GL1)∀α∈L,α*1=α;

(GL2)∀α,β∈L,α*β=β*α;

(GL3)∀α,β,γ∈L,α*(β*γ)=(α*β)*γ;

(GL4)若α≤β则存在γ∈L使得α=β*γ(可除性);

(GL5)α*∨j∈Jβj=∨j∈J(α*βj).

由于*对任意并是分配的,那么映射α*(-):L→L必有一个右伴随映射α→(-):L→L,α→β=∨{γ∈L|α*γ≤β}.

运算→称为*的剩余运算. 下面的引理归纳了*与→的一些常见性质.

引理1 设(L,≤,*)为GL-幺半群,则

(I1)0*α=0,1→α=α;

(I2)α→β=1⟺α≤β;

(I3)α*(α→β)≤β,(α→β)*(β→γ)≤α→γ;

(I4)α→(β→γ)=(α*β)→γ=β→(α→γ);

(I5)α≤(α→β)→β;

(I6)(∨j∈Jαj)→β=∧j∈J(αj→β);

(I7)α→(∧j∈Jβj)=∧j∈J(α→βj);

(I8)α≤β⟹α→γ≥β→γ,γ→α≤γ→β.

引理2[5]设(L,≤,*)为GL-幺半群,∀α∈L,B⊆L有α∧(∨B)=∨β∈B(α∧β).

即,完备格L是一个frame.

称三元组(L,≤,⊗)是一个预幺半群,其中(L,≤)是完备格,⊗是L上的一个二元运算满足如下公理[2]: (CL1)α≤α⊗1,α≤1⊗α;(CL2)α≤β,γ≤δ⟹α⊗γ≤β⊗δ;(CL3)对任意非空集族{βj|j∈J},α⊗∨j∈Jβj=∨j∈J(α⊗β),(∨j∈Jβj)⊗α=∨j∈J(βj⊗α).

注意到二元运算⊗不一定是可交换的,可结合的.(CL3)中的分配性也只针对非空并.显然,GL-幺半群一定是预幺半群,反之则不一定成立.

称四元组(L,≤,⊗,*)为强化的预幺半群,其中(L,≤,⊗)为预幺半群,(L,≤,*)为GL-幺半群且满足如下公理:

(ECL)对∀α1,α2,β1,β2∈L, (α1⊗β1)*(α2⊗β2)≤(α1*α2)⊗(β1*β2).

若(L,≤,∧)是一个frame,(L,≤,*)是GL-幺半群,那么(L,≤,*,*)和(L,≤,∧,*)都是强化的预幺半群. 更多的例子请参考文献[2].

设X是一个集合,(L,≤,⊗,*)是强化的预幺半群.记X上的所有L-集子集为LX,则L上的运算*,→,∧,∨,⊗可以以逐点的方式传递到LX上:任取λ,μ∈LX,R⊆LX,

(λ*μ)(x)=λ(x)*μ(x);(λ→μ)(x)=λ(x)→μ(x);(λ⊗μ)(x)=λ(x)⊗μ(x);(∨R)(x)=∨μ∈Rμ(x);(∧R)(x)=∧μ∈Rμ(x).

2 滤子与L-滤子

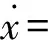
定义1[2,5]称映射F:LX→L为集合X上满层的L-滤子,若∀λ,μ∈LX,α∈L:

(LF1)F(0X)=0X,F(1X)=1X; (LF2)λ≤μ⟹F(λ)≤F(μ);(LF3)F(λ)⊗F(μ)≤F(λ⊗μ); (LF4)∀α∈L,α*F(λ)≤F(αX*λ).

例(1) 对集合X上的每一个点x,映射[x]:LX→L,[x](λ)=λ(x)为X上满层的L-滤子,称为由x生成的主L-滤子.

接下来考虑Γ(X)与FLs(X)之间的2个对应.

对F∈FLs(X),规定ΦF={A⊆X|F(1A)=1}.

对F∈Γ(X),规定FF(λ)=∨{α|λα∈F},其中λα={x|λ(x)≥α}.

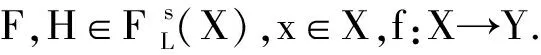
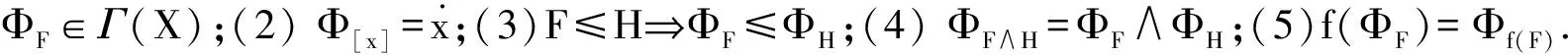
证明(1)由(LF1)可知X∈ΦF且∅∉ΦF.若A∈ΦF,A⊆B则由(LF2)我们有F(1B)≥F(1A)=1,也就是说,B∈ΦF.设A,B∈ΦF,由于1是(L,≤,⊗)的单位元,故F(1A∩B)=F(1A⊗1B).又由(LF3)得F(1A∩B)=F(1A⊗1B)≥F(1A)⊗F(1B)=1,即A∩B∈ΦF.从而得证ΦF∈Γ(X).

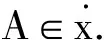
(3) 设A∈ΦF,F≤H,则H(1A)≥F(1A)=1从而A∈ΦH.

(4) 由下面的等价立得:A∈ΦF∧H⟺(F∧ H)(1A)=1⟺F(1A)∧H(1A)=1⟺A∈ΦF∧ΦH.

(5) 设A∈Φf(F),则F(1A∘f)=f(F)(1A)=1. 注意到1A∘f=f-1(A)∈ΦF,又因为f(f-1(A))⊆A,故A∈f(ΦF).相反地,设A∈f(ΦF),则必存在一个B∈ΦF使得f(B)⊆A.这意味着B⊆f-1(A)=1A∘f∈ΦF,换言之,F(1A∘f)=f(F)(1A)=1,因此A∈Φf(F).

在下文中,当涉及ΦF时,总假设1是(L,≤,⊗)的单位元.

命题2 设F,S∈Γ(X),x∈X,f:X→Y.则

证明(1)(LF1):∀α∈L,由于(1X)α=X∈F,(0X)α=∅∉F,故FF(1X)=1且FF(0X)=0.

(LF2): 当λ≤μ时,λα⊆μα.因此若λα∈F则μα∈F.故FF(λ)=∨{α|λα∈F}≤∨{β|μβ∈F}=FF(μ).

(LF3):设λα,μβ∈F,那么由(λ⊗μ)α⊗β⊇λα⊗β∩μα⊗β∈F得(λ⊗μ)α⊗β∈F. 故

FF(λ)⊗FF(μ)=∨{α|λα∈F}⊗∨{β|μβ∈F}=∨{α⊗β|λα∈F,μβ∈F}≤∨{α⊗β|(λ⊗μ)α⊗β∈F}≤∨{γ|(λ⊗μ)γ∈F}=FF(λ⊗μ).

(LFs): 由λβ⊆(αX*λ)α*β得λβ∈F⟹(αX*λ)α*β∈F成立. 从而

α*FF(λ)=α*∨{β|λβ∈F}=∨{α*β|λβ∈F}≤∨{α*β|(αX*λ)α*β∈F}≤∨{γ|(αX*λ)γ∈F}=FF(αX*λ).

(3) 任取λ∈LX,有FF(λ)=∨{α|λα∈F≤S}≤∨{α|λα∈S}≤FS(λ).

(4) 任取λ∈LX,由引理2得,

FF(λ)∧FS(λ)=∨{α|λα∈F}∧∨{β|λβ∈S}=∨{α∧β|λα∈F,λβ∈S}≤∨{α∧β|λα∧β∈F∧S}≤∨{γ|λγ∈F∧S}=FF∧S(λ).

由式(3)得FF∧FS(λ)≥F(F∧S)(λ).从而结论得证.

(5) 任取μ∈LY,有f(FF)(μ)=FF(μ∘f)=∨{β|(μ∘f)β∈F}=∨{β|μβ∈f(F)}=Ff(F)(μ).

接下来,给出上述构造与Höhle[2]的构造FF之间的关系:设F∈Γ(X),定义FF如下

定理1 若F∈Γ(X),则FF=FF.

证明(1) 任取λ∈LX,易见λ=∨β∈L(βX*1λβ). 从而FΦH(λ)=∨{β|λβ∈ΦH}=∨{β|H(1λβ)=1}.对任意α∈L,若H(1λα)=1则H(λ)=H(∨β∈L(βX*1λβ))≥H(αX*1λα)≥α*H(1λα)=α*1=α.

又由α的任意性得FΦH(λ)≤H(λ).

(2) 由下面的等价立得:

A∈ΦFF⟺∨{α|(1A)α=A∈F}=1⟺A∈F.

下面的定理说明了ΦF是含在F中的最大的滤子.

证明由上面的定理得FΦF≤F,从而ΦF≤∨{S|FS≤F }.另一方面,对每一个S满足FS≤F且A∈S我们有F(1A)≥FS(1A)=1,于是,A∈ΦF.因此由S的任意性,ΦF≥∨{S|FS≤F }.

3 对角滤子与对角L-滤子

对角(L-)滤子在(模糊)拓扑学中的作用十分重要.一方面,它可以用来刻画收敛结构的拓扑性[10],另一方面它也可以用来刻画正则性[4]. 本节我们将研究对角滤子与对角(满层的)L-滤子之间的关系.

设L是完备格,x,y∈L.如果对所有的定向子集D⊆L,总有y≤supD蕴含着d∈D使得x≤d,则称x-waybelowy,记作x≪y.记x={y∈L|y≪x},若对所有x∈L都有x=supx,则称完备格L是连续的.连续格L上的≪关系满足如下性质:对于任意定向子集D,若x≪z≤supD,则存在d∈D使得x≪d[12].

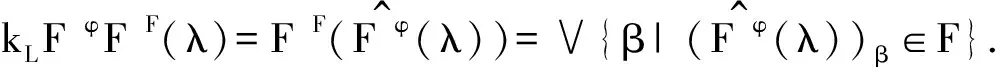
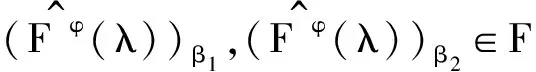
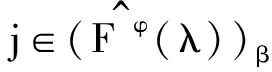
kLFφFF(λ)≤{α|λα∈kφF}=FkφF(λ).

4 结 语

本文建立了经典滤子与多值滤子之间的联系,这为进一步研究经典拓扑与多值拓扑[2,6]关系奠定了基础. 在将来的工作中,我们将通过(多值)滤子的收敛来研究经典拓扑性质(比如紧、分离、连通、正则)与多值拓扑性质之间的联系.

参考文献:

[1]PreussG.FundationsofTopology[M].London:KluwerAcademicPublishers, 2002.

[2]HöhleU,RodabaughSE(Eds.).MathematicsofFuzzySets:Logic,TopologyandMeasureTheory,TheHandbooksofFuzzySetsSeries[M].London:KluwerAcademicPublishers, 1999.

[3]JägerG.AcategoryofL-fuzzyconvergencespaces[J].QuaestionesMathematicae, 2001(24): 501-517.

[4]JägerG.Lattice-valuedconvergencespacesandregularity[J].FuzzySetsandSystems, 2008(159): 2488-2502.

[5]OrpenD,JägerG.Lattice-valuedconvergencespaces:extendingthelatticescontext[J].FuzzySetsandSystems, 2012(190):1-20.

[6]ZhangDexue.Anenrichedcategoryapproachtomanyvaluedtopology[J].FuzzySetsandSystems, 2007,158: 349-366.

[7]FangJinming.StratifiedL-orderedconvergencestructures[J].FuzzySetsandSystems, 2010(161):2130-2149.

[8]李令强,金秋.多值滤子及其应用[J]. 山东大学学报:理学版,2007,42(12): 29-32.

[9]LiLingqiang,JinQiu.OnadjunctionsbetweenLim,SL-Top,andSL-Lim[J].FuzzySetsandSystems, 2011(182):66-78.

[10]LiLingqiang,JinQiu.OnstratifiedL-convergencespaces:Pretopologicalaxiomsanddiagonalaxioms[J].FuzzySetsandSystems, 2012(204): 40-52.

[11]马英,李令强,孟广武,等. L-外部空间范畴与L-拓扑空间范畴[J]. 烟台大学学报:自然科学与工程版, 2012, 25(1):16-18.

[12]李颜霞,李令强,孟广武，等. 层次闭包空间的紧性[J]. 烟台大学学报:自然科学与工程版, 2012, 25(2):82-85.

[13]GierzG,HofmannKH,KeimelK,etal.ContinuousLatticesandDomains[M].Cambridge：CambridgeUniversityPress, 2003.