针对不稳定对象的改进动态矩阵控制

张 诚 佃松宜

(1.四川建筑职业技术学院，四川 德阳 618000；2.四川大学，成都 610065)

20世纪70年代中期，动态矩阵控制(Dynamic Matrix Control，DMC)就应用在美国壳牌石油公司的生产装置上[1,2]。1979年，Cutler C R和Ramaker B L在美国化工年会上首次介绍了这一算法[3]。几十年来，动态矩阵控制在参数优化、多变量系统和与智能控制相结合方面有很大的发展[4,5]。目前，动态矩阵控制在工业控制领域中获得了大量成功的应用[6,7]。由于动态矩阵控制算法是基于线性对象的有限阶跃响应的非参数模型，所以它只适用于渐近稳定的线性对象，不能直接用于不稳定的被控对象。对于不稳定对象的动态矩阵控制研究，席裕庚提出将传统PID控制与动态矩阵控制相结合的控制策略[1]；孙欣等提出将动态矩阵控制与状态反馈结合起来的控制策略[8]。针对这一问题，笔者基于传递函数互质分解的现代频域法，提出一种新的改进动态矩阵控制策略。

1 控制系统设计①

笔者提出的改进动态矩阵控制的结构如图1所示。采用现代频域法中的互质分解法设计内环控制器D[9]，得到稳定的广义对象，然后再针对广义对象进行动态矩阵控制设计。这样做的好处是不仅可以得到保证内环稳定的所有控制器D，而且还可以利用频域优化理论来优化内环控制器，使内环的抗扰性和鲁棒性达到最优。也就是说，如果能够最大限度地改善内环的抗扰性，并将内环对受控对象模型失配的敏感度降到最低，就间接地改善了整个DMC系统的抗扰性和鲁棒性。利用内环控制器可调节系统的抗扰性和鲁棒性，并通过H2理论优化系统的动态性能[10]。

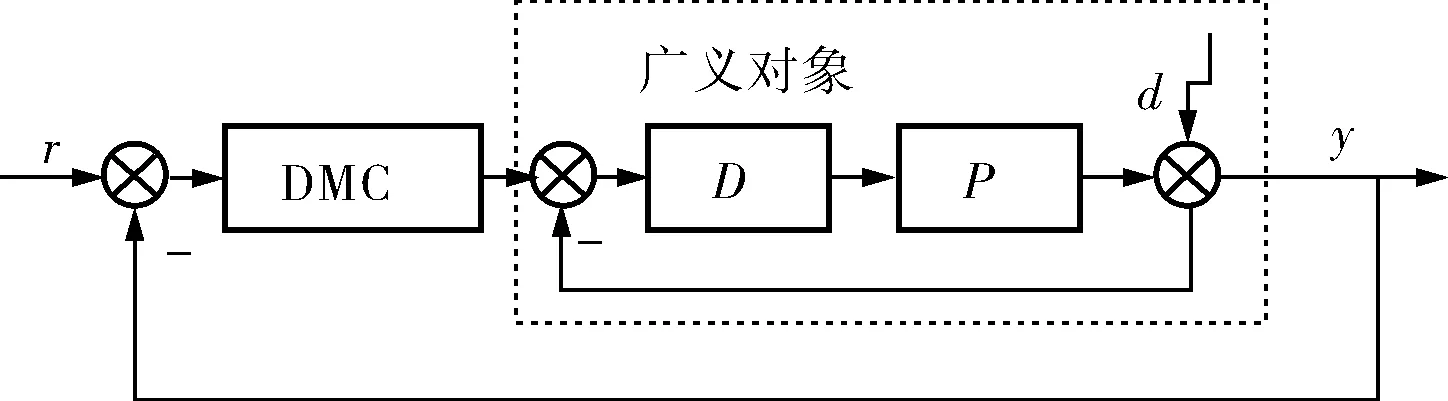
图1 控制系统结构

1.1 内环控制器D的设计

采用现代频域法的互质分解法来对控制器D进行设计[11]。将对象P分解为：

(1)

输入r分解为：

(2)

扰动d分解为：

(3)

其中nP、dP、d1、dd1、dr1、αr、αd∈H∞，dr1、dd1为单模函数，αr、αd的零点全在不稳定域，设αc为αr和αd的最小公倍式，则可以得到所有保证闭环系统稳定和稳态无差的控制器D：

(4)

其中q为自由参数；xP、yP满足Bezout等式nPxP+αcdPyP=1。

当系统没有模型失配时，将干扰d到输出y的传递函数定义为敏感性函数，代表干扰对输出的影响。当系统存在模型失配时，敏感性函数同时也是闭环传递函数的相对误差与对象模型的相对误差之比，反映模型失配对系统的影响。因此控制系统的敏感性函数为：

(5)

采用H2优化方法来优化敏感性函数，使扰动和模型给系统带来的影响最小。

当扰动未知时，取性能指标为J=‖W1S‖2，其中W1为加权函数，W1∈H2，反映扰动d或对象模型失配的频谱。当扰动已知时，可取性能指标为J=‖Sd‖2。因为D是基于互质分解方法设计的，将式(4)代入式(5)得：

S=αc(yp-qnp)dp

(6)

求出使J最小的q就可以得到抗扰性能和鲁棒性能最优的控制器D。

1.2 动态矩阵控制算法

动态矩阵控制是一种基于模型预测、滚动优化和反馈校正的控制算法[1]，通过以下3个步骤实现：

a. 得到稳定的广义对象后，对该对象进行单位阶跃响应实验，适当截断阶跃响应曲线得到阶跃响应采样序列a=[a1,a2,…,aN]T，得到未来P个时刻的输出预测值yM(k)=y0(k)+A×ΔuM(k)，其中A是系统单位阶跃响应系数阵；

b. 利用实际输出和预测输出的误差e(k+1)来修正预测值；

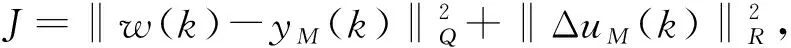
2 设计举例与仿真结果

其中ε越小越接近最优解。

对广义对象做阶跃响应实验，在t=9s时截断曲线，响应值误差范围为±0.005，取N(N=30)个采样值。预测时域p=10，控制时域M=2，误差加权系数q=1，控制增量加权系数r=2，反馈校正系数h=0.01，根据DMC算法，得到最优控制。

在t=10s时加入幅值为0.2的阶跃扰动，图2是本文方法在参数ε取不同值时的仿真结果。

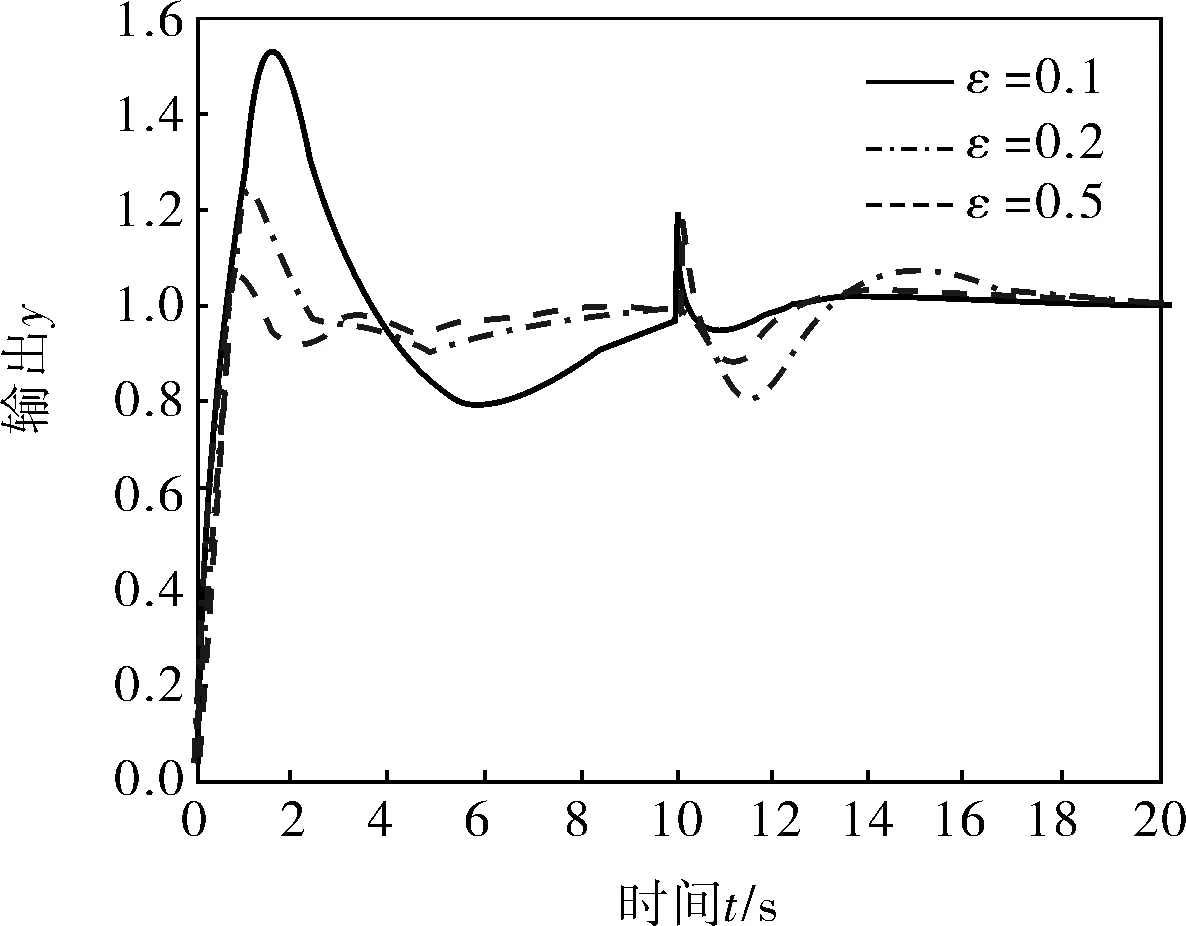
图2 ε取不同值的仿真结果

由图2可以看出，ε越小，响应越平滑，响应速度越快，超调越小，抑制干扰，能力越强。

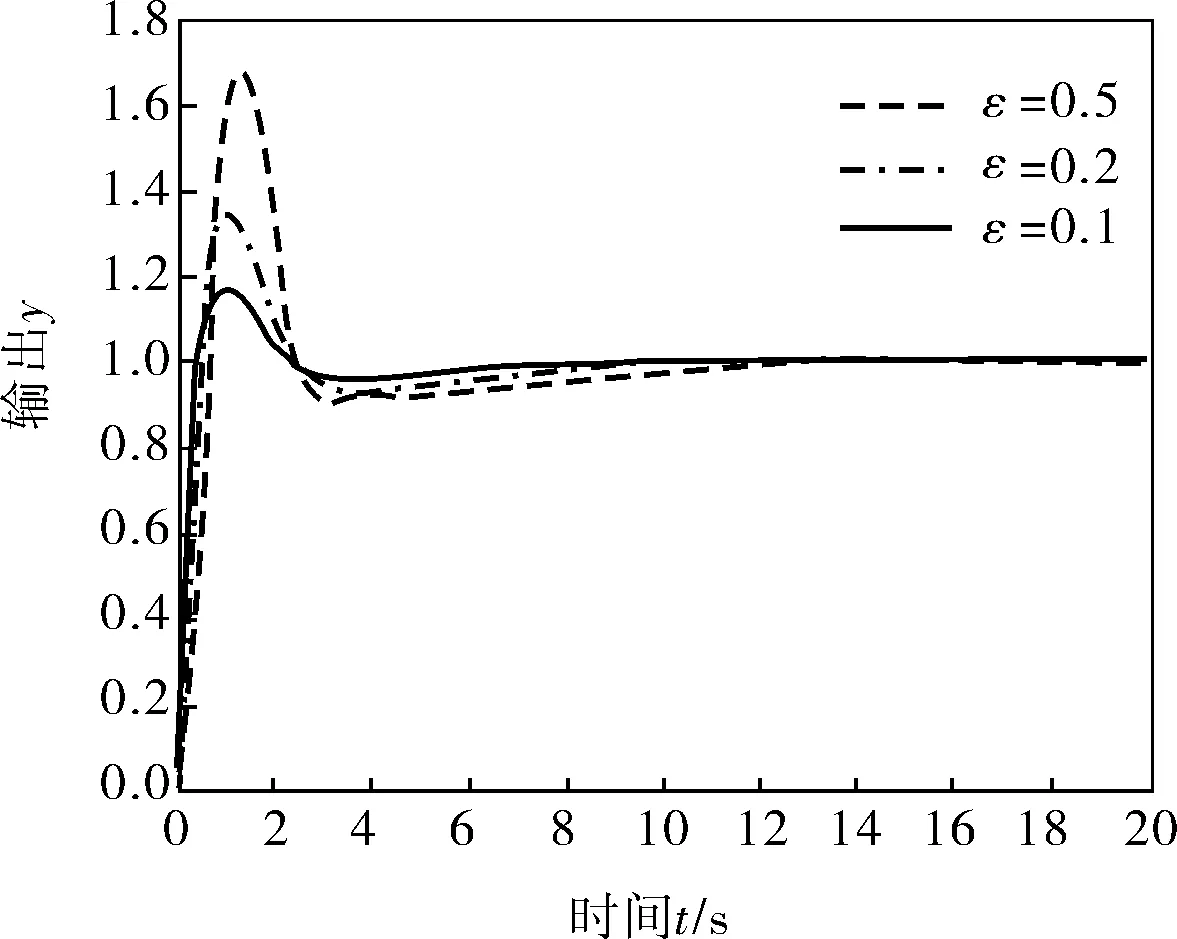
图3 有模型失配时ε取不同值的仿真结果

由图3可以看出，ε越小，系统的鲁棒性越好。

文献[8]通过设计状态反馈增益阵使闭环系统稳定，根据LQR设计状态反馈阵，再根据此稳定对象进行DMC设计。为比较本文方法与该方法，在t=15s加入幅值为0.2的阶跃扰动且系统存在相同的模型失配，设置相同的DMC参数，仿真结果如图4所示。可以看出，本文方法有更好的抗扰性和鲁棒性。

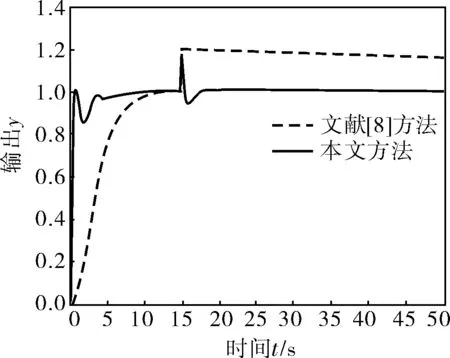
图4 本文方法与文献[8]方法的比较

3 结束语

笔者采用基于传递函数互质分解的现代频域法，提出了先利用内环控制器D稳定对象，再对稳定后的广义对象进行动态矩阵控制设计的方法，不仅能消除不稳定因素对系统的影响，而且能有效地改善系统的抗扰性和鲁棒性。对工业上常见的含有不稳定环节的系统，本文方法可以有很好的控制效果。