方位捷联平台重力仪分布式Kalman滤波初始对准算法

杨 晔，毋兴涛，杨建林，高 巍，裴 志

（1.天津航海仪器研究所，天津 300131；2.天津地区军事代表室，天津 300131）

方位捷联平台重力仪分布式Kalman滤波初始对准算法

杨 晔1，毋兴涛1，杨建林2，高 巍1，裴 志1

（1.天津航海仪器研究所，天津 300131；2.天津地区军事代表室，天津 300131）

为充分利用分布式架构重力仪各处理器并行计算的能力，解决单个处理器运行整体式 Kalman滤波所遇到的非实时性问题，设计了一种分布式 Kalman滤波对准算法。首先，给出了方位捷联平台重力仪的误差方程，建立了系统的状态方程和观测方程。然后，用协方差分析法对系统初始对准滤波方程进行处理，将原系统分解成维数相同的两个子系统，得到由两个子滤波器构成的初始对准滤波器。最后，利用Matlab建立了方位捷联平台惯导模型，分别应用整体式滤波和分布式滤波进行静基座初始对准。仿真结果表明，分布式滤波算法与整体式滤波算法具有相同的滤波精度，并且分布式滤波用时只有整体式滤波的60%，更有利于保证滤波算法的实时性。

方位捷联平台；分布式Kalman滤波；正交化；初始对准

某型重力仪采用多个低成本处理器构成分布式控制与计算系统。为充分利用系统多处理器并行计算的能力，解决单个处理器难以保证滤波实时性的问题，需要研究与系统硬件相匹配的滤波器解耦并行实现技术。国内外许多文献都针对 Kalman滤波解耦并行实现进行过研究。文献[1]研究了计算资源受限的多机器人系统中GPS-INS状态估计问题，通过比较滤波器协方差矩阵非对角元素值的大小定性分析变量间的耦合关系，并进一步使用相关系数定量分析变量间的耦合性强弱，从而将整体式滤波器进行解耦。文献[2]将MIMO控制系统中的动态结构耦合性分析方法应用于导航系统，通过分析动态直接增益矩阵对平台式惯导初始对准变量间的耦合度进行分析，忽略系统水平回路交叉耦合项后，得到两个解耦的子系统，从而降低了滤波器的维数。以上两种方法虽然能够减小滤波计算量，但由于忽略了一些变量间的耦合关系，本质上都是次优滤波，一定程度上会损失滤波精度。文献[3]将敏感器的常值零偏项当做偏差量处理，显著加快了计算速度。该方法虽然能够保证滤波的最优性但只适用于偏差量较多的情况。文献[4]使用逐次正交化法将整体式Kalman滤波器进行分解，得到的分布式滤波方法仅对低阶子系统进行计算，不仅结果最优，而且大大减少了滤波计算量，特别适合多处理器并行计算。

本文研究了方位捷联平台系统的误差特性，在文献[1]和文献[4]工作的基础上，对系统的初始对准滤波器进行设计，得到了适合在分布式架构方位捷联平台重力仪上实现的滤波方案。

1 方位捷联平台系统的误差方程

系统误差模型的推导采用扰动法，在静基座条件下，可以得到地理坐标系中误差方程为：

水平角误差方程：

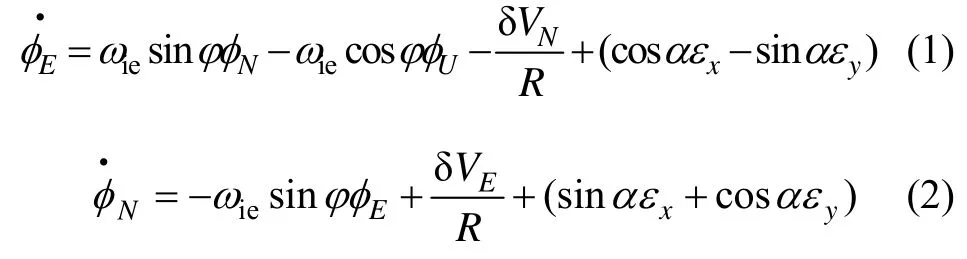
航向角误差方程：

速度误差方程：

式中，φ为地理纬度，ieω为地球自转角速度，α为方位角，xε、yε、zε为陀螺常值漂移项；ΔAx、ΔAy分别为水平加表常值零偏项。

2 Kalman滤波状态方程和观测方程

以速度误差为观测量，由以上误差方程可以建立系统的状态方程和观测方程：

3 分布式滤波设计

第一步：依据观测量的个数，通过比较相关系数大小[1]将系统划分为两个子系统。

待滤波器收敛后，得到协方差矩阵P。相关系数ijρ能够表示状态变量i、j间的耦合性强弱，ijρ表达式如式(8)所示：

计算各对状态变量间的相关系数，经比较分析后，得到子系统划分方法为：作为子系统1的状态变量，作为子系统2的状态变量。这种划分方法保证了两个子系统具有大致相同的计算量，便于算法在不同节点上并行执行。

第二步：逐次正交化分布式滤波。

将系统划分为两个子系统后，可以得到子系统1滤波状态方程和观测方程：

子系统2滤波状态方程和观测方程：

对文献[4]中滤波算法进行分析设计后，得到两个子系统逐次正交化分布式滤波计算流程如图1所示。

4 仿真及结果分析

4.1 仿真条件

仿真参数设置如表1所示。整体式滤波器参数设置为：

状态协方差阵初始值：

系统噪声协方差阵：

表1 仿真参数设置Tab.1 Parameters of simulation

观测噪声协方差阵：

分布式滤波器参数设置为：

状态协方差阵初始值：

系统噪声协方差阵：

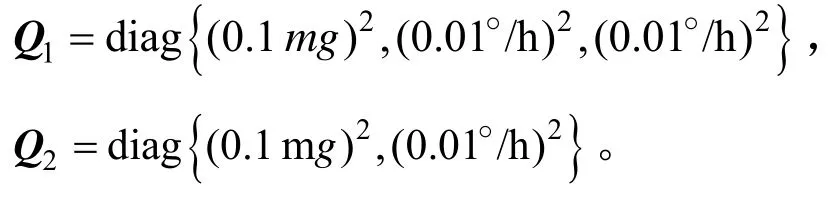
观测噪声协方差阵：

4.2 仿真结果及分析

图2～图5给出了整体式滤波对准与相同条件下分布式滤波对准仿真曲线的对比，1200 s滤波精度及用时的量化比较如表2所示。

图2 东向误差角估计误差Fig.2 Estimated error of eastern error angle

从图2～图5及表2可以分析出：

① 1200 s滤波结束时，两种滤波方式状态协方差阵Pii(k/k)对角线上元素基本相同，证明逐次正交化分布式滤波仍然是最优滤波，表2中滤波估计值的对比也符合这一论断；

② 分布式滤波用时只有整体式滤波的 60%，明显地减小了运算量，增强了滤波实时性。

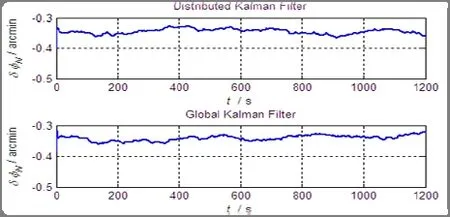
图3 北向误差角估计误差Fig.3 Estimated error of northern error angle

图4 航向误差角估计误差Fig.4 Estimated error of heading error angle

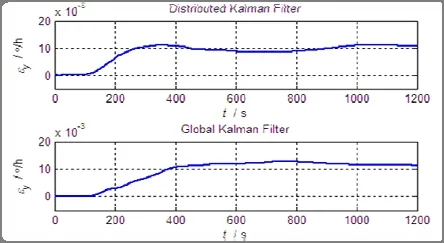
图5 平台系y轴方向陀螺常值漂移Fig.5 Estimation ofy-axis gyroscope drift

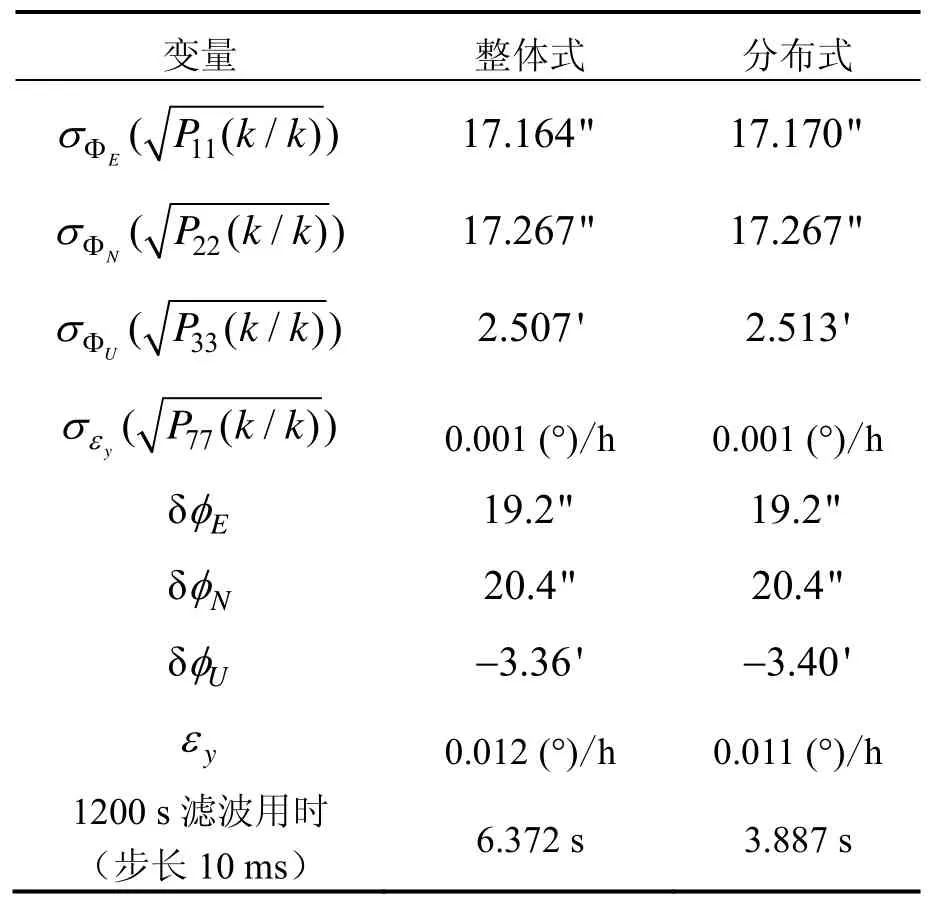
表2 滤波精度及用时的量化比较Tab.2 Comparison of filtering accuracy and cost of time

5 结 论

通过对方位捷联平台重力仪初始对准滤波器进行逐次正交化设计，将整体式滤波器分解成两个维数较低的子滤波器。仿真结果证明：逐次正交化分布式滤波在保持滤波最优性的同时大大减小了计算量，适合在分布式架构重力仪上实现，并且系统阶次越高，分割子系统就越多，这种优势越明显。下一步可以研究分布式滤波技术在重力匹配组合导航系统中的应用，解决组合导航系统的滤波非实时性问题。

（References）:

[1]Wachter L M,Ray L E.GPS-INS state estimation for multi-robot systems with computational resource constrains[C]//2009 American Control Conference.2009: 561-567.

[2]郝颖，谈振藩，李东明.动态结构耦合性分析方法在导航系统中的应用[J].中国惯性技术学报，2005，13(3)：26-29.HAO Ying,TAN Zhen-fan,Li Dong-ming.Application of dynamic measurement of structural interaction in navigation system[J].Journal of Chinese Inertial Technology,2005,13(3): 26-29.

[3]柳明，向礼，刘雨，等.一种新的惯导平台静基座快速初始对准方法[J].上海航天，2010(5)：51-54.LIU Ming,XIANG Li,LIU Yu,et al.A new fast inertial alignment method of inertial navigation platform on stationary base[J].Aerospace Shanghai,2010(5): 51-54.

[4]Hassan M,Salut G,Sigh M,et al.A decentralized algorithm for the global Kalman filter[J].IEEE Transactions on Automatic Control,1978,23(2): 262-267.

[5]Weihua Ma,Jianjun Luo,Jianping Yuan,et al.SINS/GPS/SS reduced-order Kalman filter design based state decoupling for space application[C]//4thIEEE Conference on Industrial Electronics And Applications.2009: 2596-2600.

[6]FU Qiang-wen,QIN Yong-yuan,LI Si-hai,et al.Optimal two-position alignment method based on parameter identification[J].Journal of Chinese Inertial Technology,2013,21(4): 430-434.

[7]Takaya K.Transputer-like multicore parallel processing on the array of arm Cortex-M0 microprocessors[C]//2012 25thIEEE Canadian Conference on Electrical and Computer Engineering.2012: 1433-1437.

[8]Yang Chao,Wu Junfeng,Zhang Wei,et al.Schedule communication for decentralized state estimation[J].IEEE Transactions on signal processing,2013,61(10): 2525-2536.

[9]Wang J H,Chen J B.Adaptive unscented Kalman filter for initial alignment of strapdown inertial navigation system[C]//2010 International Conference on Machine Learning and Cybernetics.2010,Vol.3: 1384-1389.

[10]Oruc S,Sijs J.Optimal decentralized Kalman filter[C]//2009 17thMediterranean Conference on Control &Automation.Thessalonlkl,Greece,2009: 803-809.

Distributed Kalman filter initial alignment algorithm for azimuth strapdown platform gravimeter

YANG Ye1,WU Xing-tao1,YANG Jian-lin2,GAO Wei1,PEI Zhi1
(1.Tianjin Navigation Instrument Research Institute,Tianjin 300131,China;2.Tianjin Military Representative Office,Tianjin 300131,China)

A distributed Kalman filter alignment algorithm is developed in order to use the parallel computing ability of the distributed architecture gravimeter to solve the non real-time implementation of filtering based on one single processor.Firstly,the error equations of the azimuth strapdown platform gravimeter are deduced,and the state equations and observation equations are built.Secondly,an error covariance analytical method is applied to the filtering equations,and the system is decentralised into two subsystems with the same dimension.In this way we get the initial alignment filter formed by the two subfilters.Finally,the azimuth strapdown platform model is built by using Matlab,and stationary base alignment is implemented by using global Kalman filter and distributed Kalman filter separately.The simulation results show that the distributed filter has the same filtering accuracy and costs only 60% of time compared with the global one,which is favorable to ensure the real-time performance of the algorithm.

azimuth strapdown platform; distributed Kalman filter; orthogonalization; initial alignment

U666.1

：A

1005-6734(2014)02-0191-04

10.13695/j.cnki.12-1222/o3.2014.02.009

2013-12-20；

：2014-01-27

国家“863”计划课题（2011AA060501）

杨晔（1968—）男，研究员，硕士生导师，从事导航、制导与控制系统研究。E-mail：liuyuyangye@eyou.com