四旋翼飞行器分散PID神经元网络控制

陈彦民，何勇灵，孔令博，周岷峰

（北京航空航天大学 交通科学与工程学院，北京 100191）

四旋翼飞行器分散PID神经元网络控制

陈彦民，何勇灵，孔令博，周岷峰

（北京航空航天大学 交通科学与工程学院，北京 100191）

针对四旋翼飞行器的非线性控制问题，提出了一种分散PID神经元网络（PIDNN）控制方法。首先通过牛顿—欧拉方程建立了四旋翼飞行器的动力学模型。其次，提出了一种嵌套控制器，内环基于分散PIDNN方法以实现姿态控制，外环采用经典的PID控制方法，PIDNN控制器的在线学习通过误差反向传播法实现。搭建了自主研制的四旋翼飞行器系统，并通过实验的方式研究了控制器的控制性能。实验结果表明控制器具有较强的控制稳定性、机动性和鲁棒性。

四旋翼飞行器；分散PID神经元控制；误差反向传播算法；路径跟踪

近来，作为垂直起降无人机系列中的一种，四旋翼飞行器在军事和民用领域得到了越来越广泛的应用。相比固定翼飞机，四旋翼飞行器具有低空飞行、定点悬停等特性。相比于传统的直升机，四旋翼飞行器具有结构简单、机动性强、体积小、成本低及隐蔽性好等特性。这些特性使得四旋翼飞行器能够高效可靠地在有限的空间内飞行。

四旋翼飞行器由机身和四个旋翼组成，升力由四个旋翼提供。旋翼分为转向相反的两组，以抵消因旋转而产生的反扭力矩。通过差动改变同组旋翼的转速，可以实现滚转和俯仰运动；通过控制两组旋翼的反扭力矩，可以实现偏航运动。由于四旋翼飞行器只有四个驱动力但是需要完成六个自由度的运动，所以其是一个欠驱动、强耦合的非线性系统，而且其受外界扰动的影响较大[1]。近年来，很多文献对四旋翼飞行器的控制问题进行了研究，取得了大量的研究成果。比较典型的方法有PID控制[2-4]，自适应控制[5-7]，反演控制[8-13]，滑模变结构控制[14-15]，鲁棒控制[16-17]和神经网络控制[18-19]等。

PIDNN控制是一种新的控制方法，它结合了PID控制和神经网络控制的优点，它并不是PID控制和神经网络控制的简单组合，不是用神经元网络选择和整定PID参数，而是分别定义了具有比例、积分、微分功能的神经元，从而将PID控制规律融合进神经元网络之中[20-21]。

PIDNN控制方法的优点如下：1） 比神经网络控制的响应速度快；2）比传统PID控制器的适应性好；3）硬件实现简单。所以，本文以PIDNN方法为基础，设计了一种控制器，以期望解决四旋翼飞行器的控制问题。

本文设计的基于分散PIDNN控制的四旋翼飞行器控制器由内环姿态控制器和外环位置控制器组成。姿态控制器采用分散PIDNN控制方法，位置控制器则采用经典PID控制。将该控制器运用在自主研制的四旋翼飞行器上，实验结果验证了其控制的有效性。

1 四旋翼飞行器动力学模型

四旋翼飞行器由机身和四个旋翼组成，如图 1所示。假定四旋翼飞行器是刚体且结构完全对称，建立地面坐标系E={Ex,Ey,Ez}和机体坐标系B={Bx,By,Bz}。姿态角Θ=[φ,θ,ψ]T分别称为滚转角(-π/2＜φ＜π/2)、俯仰角(-π/2＜θ＜π/2)和偏航角(-π＜ψ＜π)。

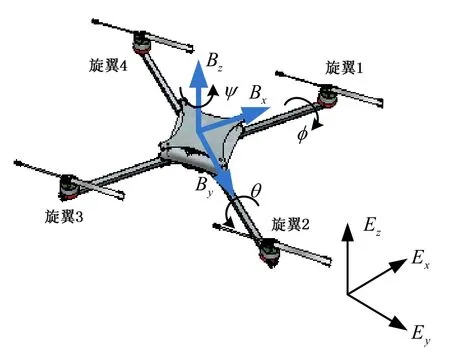
图1 四旋翼飞行器的结构简图Fig.1 Structure of quadrotor helicopter

动力学模型由平动与转动两部分构成，由牛顿—欧拉方程在地面坐标系E中建立平动方程：

式中，X= [x,y,z]T是四旋翼飞行器质心的位置，m为质量，R是坐标转换矩阵，FTi是旋翼i的升力，G= [0,0,-g]T为重力加速度。

在机体坐标系B中建立转动方程：

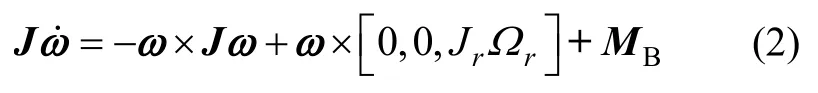
式中，J为惯性矩对角线矩阵，ω= [p,q,r]T是机体转动角速度，Jr是旋翼的转动惯量，rΩ是旋翼的相对速度：

ω×[0,0,JrΩr]项表示的是由于旋翼旋转而产生的陀螺转矩。MB是旋翼拉力引起的转矩：

式中，l是机体的臂长。

综合式(1)～(4)，可得出风场作用下四旋翼飞行器的动力学模型：

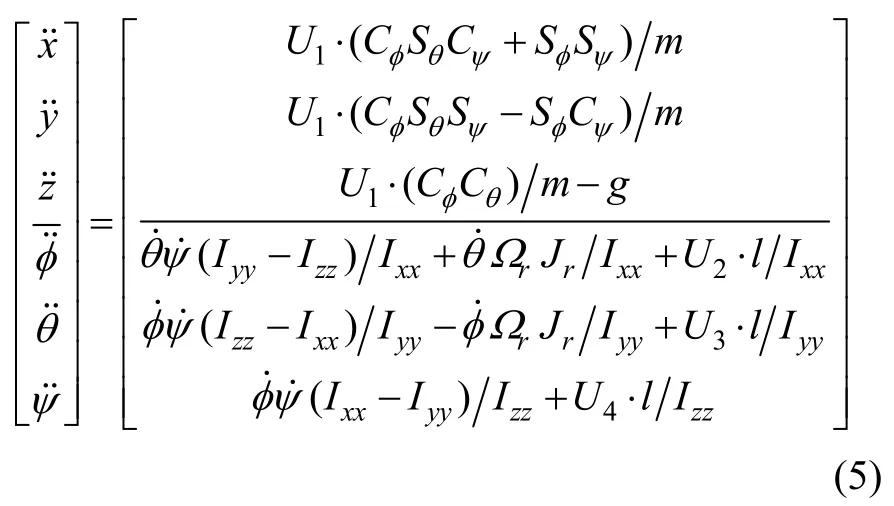
式中，U=[U1,U2,U3,U4]T为控制向量，定义为：

2 控制策略

本文所设计的控制器由内外环嵌套而成，如图2所示，内环采用PIDNN控制算法，实现姿态控制，外环采用PID控制算法，实现高度和位置的控制。由四旋翼飞行器的特点可知，外环位置的运动是由内环姿态角决定的。高度控制器根据目标高度zd和当前高度位置z计算出高度控制量U1，同时位置控制器根据目标位置xd、yd结合当前位置x、y逆向求解出目标姿态角dφ和dθ传入姿态控制器，然后姿态控制器得出滚转、俯仰和偏航控制量U2、U3、U4传至动力学模型，最后，动力学模型结合风场的影响计算出本时步系统的状态，回传至各控制器进行下一时步的计算。

图2 控制系统结构Fig.2 Structure of control system

2.1 高度控制

由(5)式中的高度方程，可得：

式中，CφCθ≠0；Pz为PID控制器，形式如下：

式中，kzP、kzI和kzD分别是控制器的比例，积分和微分系数，k为迭代次数，ts为时步。

2.2 位置控制

将U1带入式(5)中x和y方向的方程，并认为ψ很小近似为0，可得：

设计x、y方向的PID控制器为：

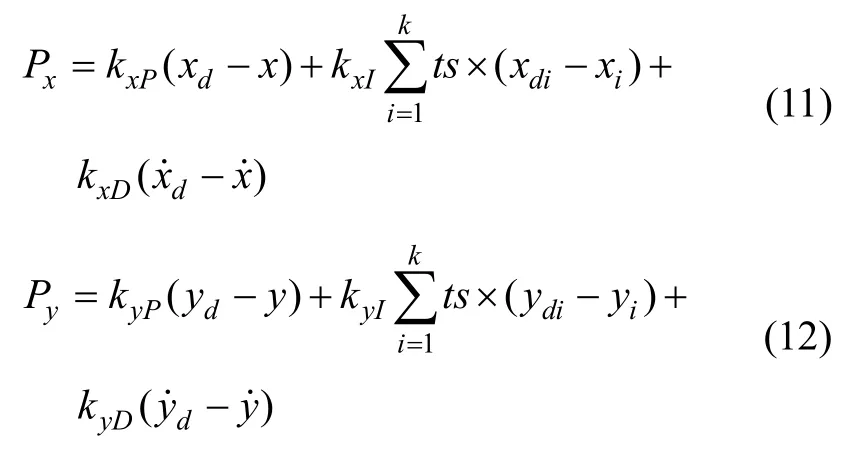
对式(9)和式(10)逆向求解，可求出目标姿态角dφ和dθ：

2.3 姿态控制

姿态控制是四旋翼飞行器控制的核心，其控制性能会极大地影响飞行的稳定性。由于PIDNN控制器具有良好的瞬态和稳态性能，对外界扰动和自身不确定性有较强的鲁棒性，故引入其作为姿态控制的方法。

姿态控制包括滚转、俯仰和偏航三个方向的控制，若采用集中控制器，其算法将会非常复杂。为了有效地控制四旋翼飞行器的姿态，为这三个姿态角独立设计PIDNN控制器，这三个PIDNN子控制器共同构成了分散PIDNN控制器，同时且独立地控制三个姿态角。分散PIDNN控制器能够减小运算负荷，提高系统反应速度而且也能简化控制器的设计。滚转角的PIDNN控制器如下所述。

2.3.1 网络结构

滚转角的PIDNN控制器为三层前向反馈网络，由输入层、隐含层和输出层构成，网络结构如图 3所示。

图3 滚转角的PIDNN控制器网络结构图Fig.3 Network structure of PIDNN controller for roll angle

●输入层

输入层有两个神经元x1=φ(k)及x2=φd(k)，φ(k)为滚转角实际值，φd(k)为滚转角设定值，其中，k为迭代次数。

●隐含层

隐含层是体现 PIDNN控制器功能的最重要的层次，包括三个神经元，分别为比例元、积分元和微分元，它们的输入uj(k)为：

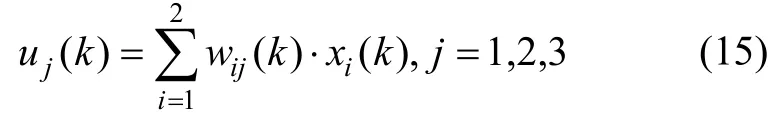
式中，wij(k)为输入层至隐含层的连接权重。三个神经元的输出分别为：

●输出层

输出层只包含一个神经元，完成网络的输出功能，输出量即为滚转角的控制量U2(k)：

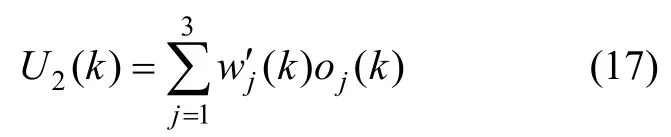
2.3.2 在线学习算法

PIDNN控制器的在线学习算法采用误差反向传播法。该算法以梯度下降法为基础，通过对网络权重值的修改，达到令目标函数E(k)值最小的目的。目标函数E(k)定义为：

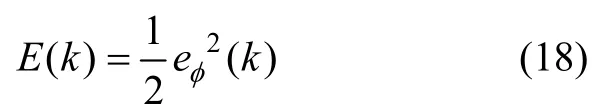
式中，eφ(k)=φd(k)-φ(k)为滚转角的误差值。在线学习算法描述如下。

●隐含层至输出层

隐含层至输出层权重迭代公式为：

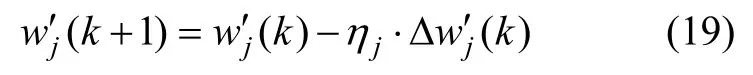
ηj为wj′的学习步长。根据反传算法，式中权重增量可表示为：

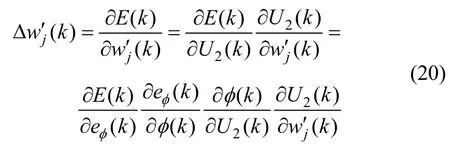
●输入层至隐含层

输入层至隐含层权重迭代公式为：

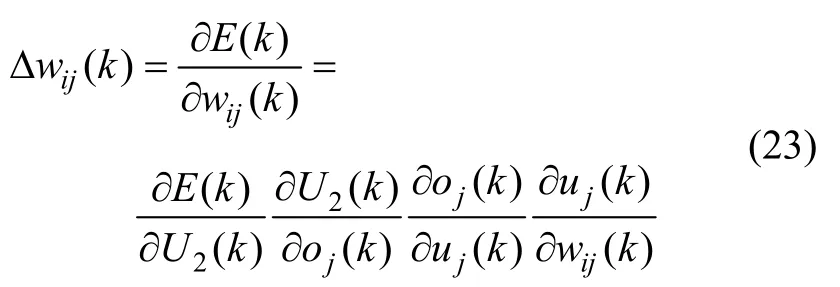
由式(15)(16)(20)和(21)，可求出：

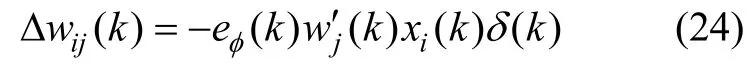
式(21)和(24)中，δ(k)值难以精确确定，这里作以下相应的简化：

3 硬件系统结构

根据四旋翼飞行器的特点和实际的飞行需求，飞行控制系统的主要模块包括主控制器模块、传感器模块、导航模块、电机控制模块、通信模块及数据采集模块等。硬件系统总体结构框图如图4所示。

3.1 主控制器模块

主控制模块是飞行控制系统的核心。处理器作为整个系统的核心控制部分，主要负责采集传感器检测到的姿态角速率、三轴的线加速度和航向信息并实时解算；根据检测到的飞行信息，结合既定的控制方案，计算输出控制量；通过通信模块与地面站进行数据的传输，实现接收控制命令，改变飞行状态和下传飞行状态数据。本课题综合考虑性能、接口、成本及开发难度等方面，选择ATMEGA 2560-16AU为系统主控芯片。

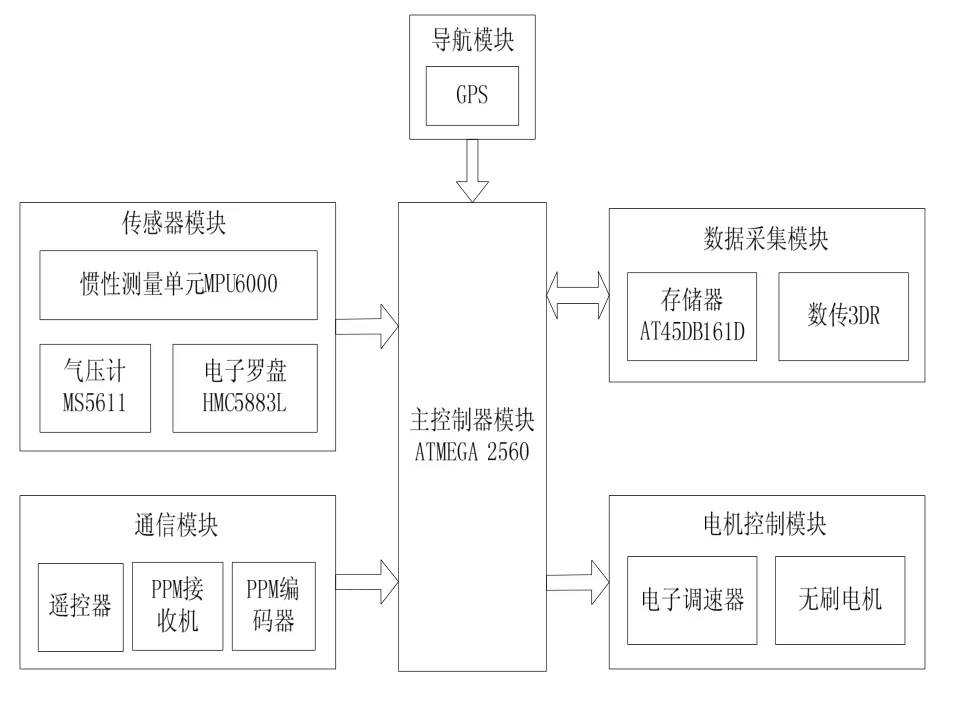
图4 硬件系统总体结构框图Fig.4 General structure of hardware system

3.2 传感器模块

传感器模块主要包括惯性测量单元、气压计、电子罗盘等。惯性测量单元选择六轴惯性测量单元MPU 6000。它集成了3轴MEMS陀螺仪，3轴MEMS加速度计，以及一个可扩展的数字运动处理器DMP，能够完成对四旋翼飞行器姿态的解析。

气压计选择MS5611，以测量飞行器当前的准确高度。电子罗盘选择霍尼韦尔公司的 HMC5883L，与导航模块配合，对GPS信号进行有效的补偿，保证导航定向信息的可靠性。

3.3 导航模块

导航模块的功能是提供飞行器当前经纬度信息，航迹方向和地速信息，采用的是高精度GPS导航。模块主芯片采用U-BLOX，能够修改并固化波特率，内带存储器，可以保存设置。飞行控制电路板如图5所示，搭建的四旋翼飞行器如图6所示。

图5 飞行控制电路板Fig.5 PCB of flight control

图6 自主搭建的四旋翼飞行器Fig.6 Independently developed quadrotor helicopter

4 实验验证

为了验证所设计控制器的性能，对搭建的四旋翼飞行器进行了路径跟踪控制实验。令四旋翼飞行器从地面点(0,0,0)起飞，依次经过点(0,0,2)、点(2,0,2)、点(2,2,2)、点(0,2,2)和点(0,0,2)，即绕边长为 2m的正方形参考轨迹一圈，最后降落回地面点(0,0,0)，姿态角的初始值均为0 rad，偏航角参考值ψd=0rad。实验结果如图7～9所示。

图7 路径轨迹（3D）Fig.7 Path trajectory (3D)

图8 位置及高度曲线Fig.8 Position and altitude

图7和图8表示的是四旋翼飞行器的路径轨迹，结果显示飞行器能够基本按照设定的参考路径飞行，由于传感器误差、系统噪声及外部不确定性干扰等原因，飞行器的轨迹略有振荡，但均在设定的参考值附近。

图9所示的是姿态角的响应曲线，由实验结果可以看到，由位置控制器生成的滚转角和俯仰角的参考值能够较为迅速地响应位置输入值的变化。姿态角的实际值与参考值的误差能够被控制在0.1rad 之内，说明分散PIDNN姿态控制器具有较为良好的性能。

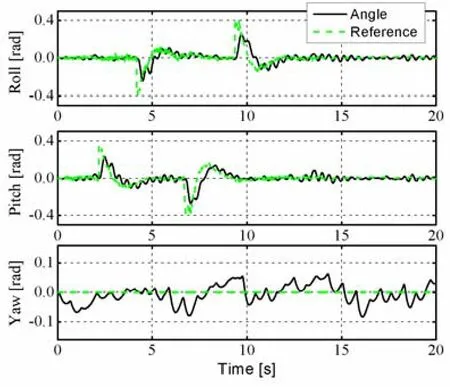
图9 姿态角响应曲线Fig.9 Attitude angle response

5 结 论

针对四旋翼飞行器的飞行控制问题，本文设计了一种新型的控制器，该控制器由PID外环控制器与分散PIDNN内环控制器组成。将此控制器应用在自主搭建的四旋翼飞行器上，进行了路径跟踪控制实验。实验结果表明，控制器能够有效地将四旋翼飞行器控制在目标状态，具有良好的控制稳定性、机动性和鲁棒性。

（References）：

[1]Abhijit D,Frank L,Kamesh S.Backstepping approach for controlling a quadrotor using Lagrange form dynamics[J].Journal of Intelligent & Robotic Systems,2009,56(1-2): 127-151.

[2]Bouabdallah S,Noth A,Siegwart R.PID vs LQ control techniques applied to an indoor micro quadrotor[C]//Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems.Sendai,Japan,2004:2451-2456.

[3]宿敬亚，樊鹏辉，蔡开元.四旋翼飞行器的非线性PID姿态控制[J].北京航空航天大学学报，2011，37(9)：1054-1058.SU Jing-ya,FAN Peng-hui,CAI Kai-yuan.Attitude control of quadrotor aircraft via nonlinear PID[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(9): 1054-1058.

[4]Wang Hong-yu,Zhao Jian-kang,Yu Wen-xian,et,al.Modelling and position tracking control for quadrotor vehicle[J].Journal of Chinese Inertial Technology,2012,20(4): 455-458.

[5]Morel Y,Leonessa A.Direct adaptive tracking control of quadrotor aerial vehicles[C]//ASME International Mechanical Engineering Congress and Exposition,Miami,USA: 2006: 155-161.

[6]Rashid M I,Akhtar S.Adaptive control of a quadrotor with unknown model parameters[C]//Proceedings of 9th International Bhurban Conference on Applied Sciences and Technology.Islamabad,Pakistan: 2012: 8-14.

[7]Mohammadi M,Shahri A M.Adaptive nonlinear stabilization control for a quadrotor UAV: theory,simulation and experimentation[J].Journal of Intelligent and Robotic Systems,2013,71(1): 1-18.

[8]何勇灵，陈彦民，周岷峰.四旋翼飞行器在风场扰动下的建模与控制[J].中国惯性技术学报，2013，21(5)：624-630.He Yongling,Chen Yanmin,Zhou Minfeng.Modeling and control of a quadrotor helicopter under impact of wind disturbance[J].Journal of Chinese Inertial Technology.2013,21(5): 624-630.

[9]Mian A A,Wang D B.Modeling and backsteppingbased nonlinear control strategy for a 6 DOF quadrotor helicopter[J].Chinese Journal of Aeronautics,2008,21(3): 261-268.

[10]Madani T,Benallegue A.Backstepping sliding mode control applied to a miniature quadrotor flying robot[C]//32nd Annual Conference on IEEE Industrial Electronics.Paris,France: 2006: 700-705.

[11]Bouabdallah S,Siegwart R.Full control of a quadrotor[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems.San Diego,USA,2007: 153-158.

[12]Raffo G V,Ortega M G,Rubio F R.Backstepping &nonlinear H∞control for path tracking of a quadrotor unmanned aerial vehicle[C]//American Control Conference.Seattle,USA,2008: 3356-3361.

[13]Bouchoucha M,Seghour S,H.Osmani M B.Integral backstepping for attitude tracking of a quadrotor system[J].Electronics and Electrical Engineering,2011,116(10): 75-80.

[14]Daewon L,Jin K H,Shankar S.Feedback linearization vs.adaptive sliding mode control for a quadrotor helicopter[J].International Journal of Control Automation and Systems,2009,7(3): 419-428.

[15]Patel A R,Patel M A,Vyas D R.Modeling and analysis of quadrotor using sliding mode control[C]//Proceedings of the Annual Southeastern Symposium on System Theory.Jacksonville,USA,2012: 111-114.

[16]Raffo G,Ortega M,Rubio F.An integral predictive nonlinear H∞control structure for a quadrotor helicopter[J].Automatica,2010,46(1): 29-39.

[17]Nicol C,Macnab C J B,Ramirez-Serrano A.Robust adaptive control of a quadrotor helicopter[J].Mechatronics,2011,21(5): 927-938.

[18]Dierks T,Jagannathan S.Neural network output feedback control of a quadrotor UAV[C]//47th IEEE Conference on Decision and Control.Cancun,Mexico,2008: 3633-3639.

[19]Nicol C,Macnab C J B,Ramirez-Serrano A.Robust neural network control of a quadrotor helicopter[C]//IEEE Canadian Conference on Electrical and Computer Engineering.Canada,2008: 1233-1238.

[20]Thanh T DC,Ahn K K.Nonlinear PID control to improve the control performance of 2 axes pneumatic artificial muscle manipulator using neural network[J].Mechatronics,2006(16): 577-587.

[21]Cong S,Liang Y.PID-like neural network nonlinear adaptive control for uncertain multivariable motion control systems[J].Industrial Electronics,2009,56(10):3872-3879.

Decentralized PID neural network control for a quadrotor helicopter

CHEN Yan-min,HE Yong-ling,KONG Ling-bo,ZHOU Min-feng
(School of Transportation Science and Engineering,Beihang University,Beijing 100191,China)

A decentralized PID neural network(PIDNN) control scheme is proposed to solve the nonlinear control problems in quadrotor helicopter.First,the dynamic model is established via Newton-Euler formalism.Then,a nested loop control approach is proposed to solve the stabilization and navigation problems in the quadrotor.A decentralized PIDNN controller is designed for the inner loop to stabilize the attitude angle.A conventional PID controller is used for the outer loop in order to generate the reference path for the inner loop.Moreover,the connective weights of the PIDNN are trained on-line by error back-propagation method.The experiment is made to study the performance of controller based on the independently developed quadrotor helicopter system,which shows that the controller has good stability,maneuverability and robustness.

quadrotor helicopter; decentralized PID neural network control; error back-propagation algorithm;path following

V 279

：A

1005-6734(2014)02-0185-06

10.13695/j.cnki.12-1222/o3.2014.02.008

2013-11-20；

：2014-03-03

航空科学基金（2011ZA51001）

陈彦民（1987—），男，博士研究生，从事飞行器非线性控制方面的研究。E-mail：13718988003@163.com

联 系 人：何勇灵（1963—），男，教授，博士生导师。Email：xkbhe@buaa.edu.cn