关于检测质量的4旋转加速度计信号叠加的频域分析

丁 昊，蔡体菁

（东南大学 仪器科学与工程学院，南京 210096）

关于检测质量的4旋转加速度计信号叠加的频域分析

丁 昊，蔡体菁

（东南大学 仪器科学与工程学院，南京 210096）

在旋转圆盘上对称安装4只高精度加速度计，加速度计信号两两相加再相减，再解调制就可以得到重力梯度值。针对上述的4旋转加速度计，研究检测质量对其信号叠加的输出频域特征，推导的频域表达式证明输出中含有高次谐波，相邻谐波的频差是圆盘旋转频率的4倍，即谐波频率分别为6倍频、10倍频、14倍频等。利用stirling公式给出了各次谐波分量幅值的近似计算方法，并进行了数值仿真，结果表明检测质量与圆盘之间的距离越近，谐波分量的幅值越大。

重力梯度仪；旋转加速度计；检测质量；频域分析；谐波；检测质量.

重力梯度测量在地球物理科学、资源勘探等领域有广泛的应用前景。国际上正在研制和发展的各种类型的重力梯度仪，其中旋转加速度计重力梯度仪已成功用于航空/航海资源勘探。上世纪七十年代，美国Bell Aerospace Textron公司研制开发了第一台基于旋转加速度计重力梯度仪的系统样机，并进行了多项实验。近年来，美国Lockheed Martin公司基于此项技术开发的全张量重力梯度仪Air-FTG以及同澳大利亚BHP Billiton公司共同研制的FALCON航空重力梯度仪已经在航空重力勘探领域展现出良好的性能[1-4]。

现在国内一些单位也对旋转加速度计重力梯度仪技术开展了一系列研究[5-7]。为了研究旋转加速度计重力梯度仪信号处理和标定，下面将研究检测质量位置变化对旋转圆盘上的4个加速度计输出信号叠加的频率特征，建立输出信号的频域模型，分析信号和各次谐波分量的幅值关系。

1 4旋转加速度计信号叠加的频域特征

4只高精度加速度计对称安装在一个半径为r的圆盘上，加速度计的敏感轴指向圆盘圆周的切线方向，相对两只加速度计的敏感轴方向相反。当圆盘以角速度ω旋转时，4只加速度计的输出分别两两相加再相减，再进行解调就可得到重力梯度分量。如果圆盘外有一检测质量m，当其接近或者远离圆盘时，研究 4只旋转加速度计信号叠加后的输出。

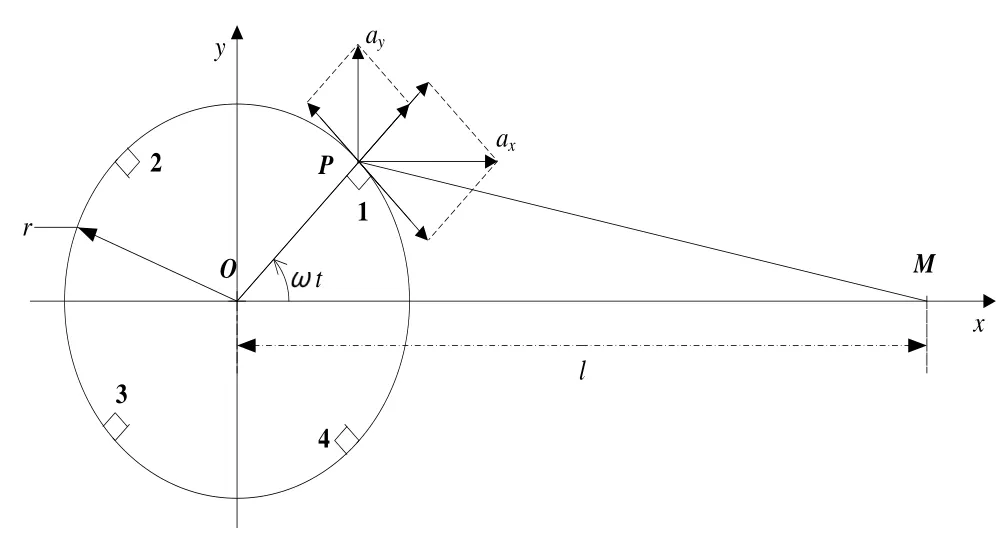
图1 以圆盘圆心O为原点建立坐标系Fig.1 The coordinate frame origin at the disc center

如图1所示，以圆盘圆心O为原点建立坐标系，圆盘位于xy平面上，x轴通过质点M在xy平面上的投影。如果圆盘圆心O与质点M在xy平面上的投影之间的距离为l，则M的坐标为(l,0,z0)。t时刻加速度计1旋转到P点，设圆盘旋转的角速度ω，t时刻圆盘转过的角度为ωt，那么加速度计1所在的P点的坐标就是。

质点M对空间中(x,y,z)位置的引力加速度，在x轴方向上的分量

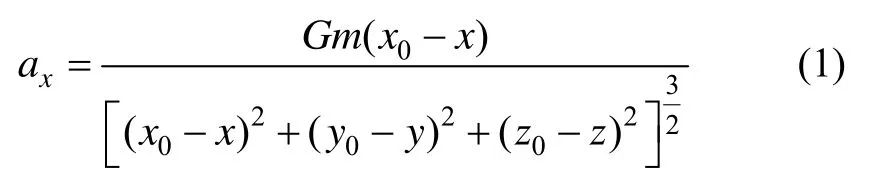
在y轴方向上的分量

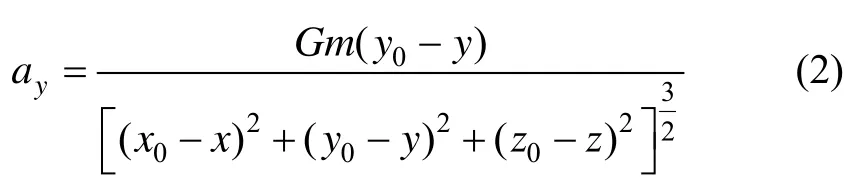
式中，G是万有引力常数。

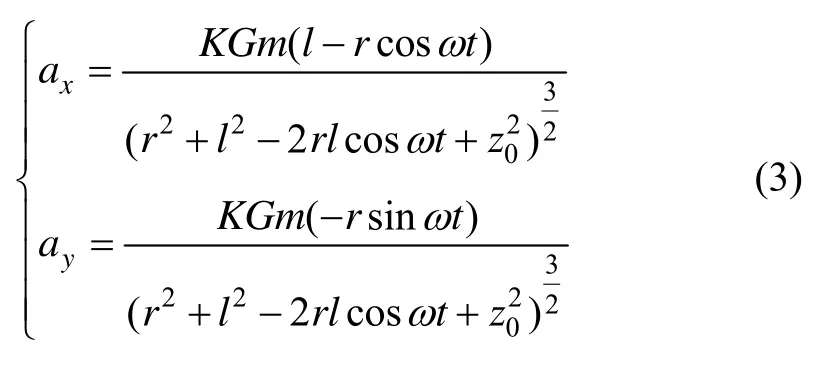
将P点坐标以及分别带入式(1)和式(2)，可得：位于P点的加速度计 1，把敏感轴方向上的输入加速度转换成输出：

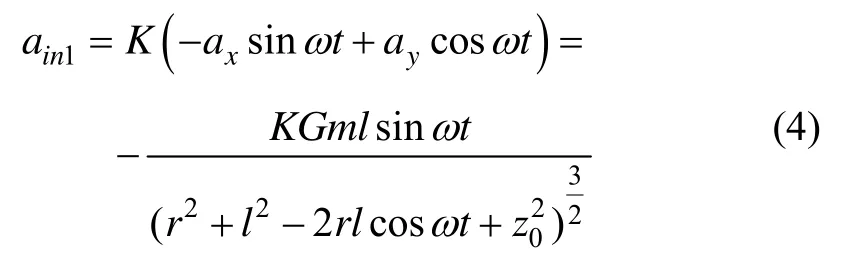
式中，K是加速度计1的标度因数。

圆盘上的其它三只加速度计由于安装位置的对称性，与上述位于P点的加速度计1转过的角度依次相差π/2。由于重力梯度仪对加速度计标度因数采取在线反馈调节技术，4只加速度计的标度因数差别很小，假设彼此相等均为K。同理可得到其它三只加速度计由于检测质量产生的输出。

第2只加速度计：

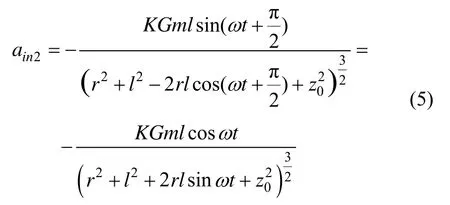
第3只加速度计：

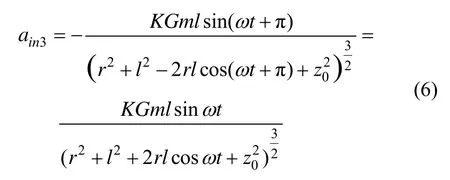
第4只加速度计：

式中，α=l/r，即质点到圆盘中心的距离与圆盘半径之比。各个加速度计的输出为：

根据式(12)得到 4加速度计输出时域图。通过FFT，可得到相应的频谱图，见图2。

虽然采用这种方法可以计算出4加速度计输出信号中的频谱分布的数值，但是只能针对已知参数的特定情况来个别求解，对4加速度计输出的频域分析存在很大的局限性。

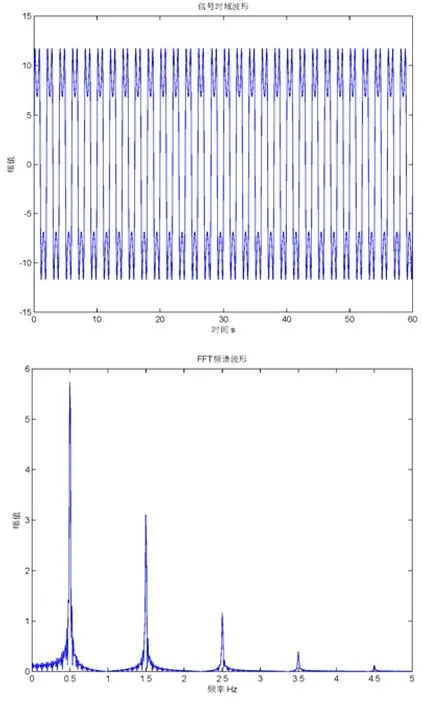
图2 4加速度计输出的时域和频域图.Fig.2 The output of four accelerometers in time domain and in frequency domain.

为了对式(12)在频域上进行讨论，利用如下的三角函数乘幂公式：

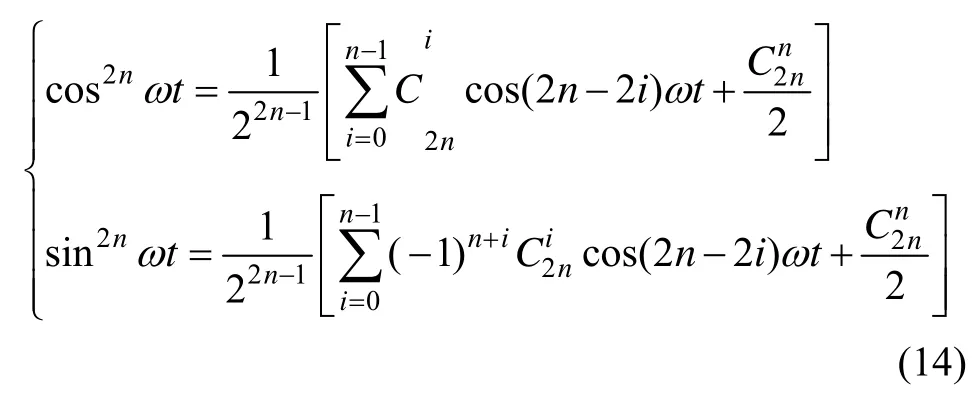
代入P(ωt)，可得：

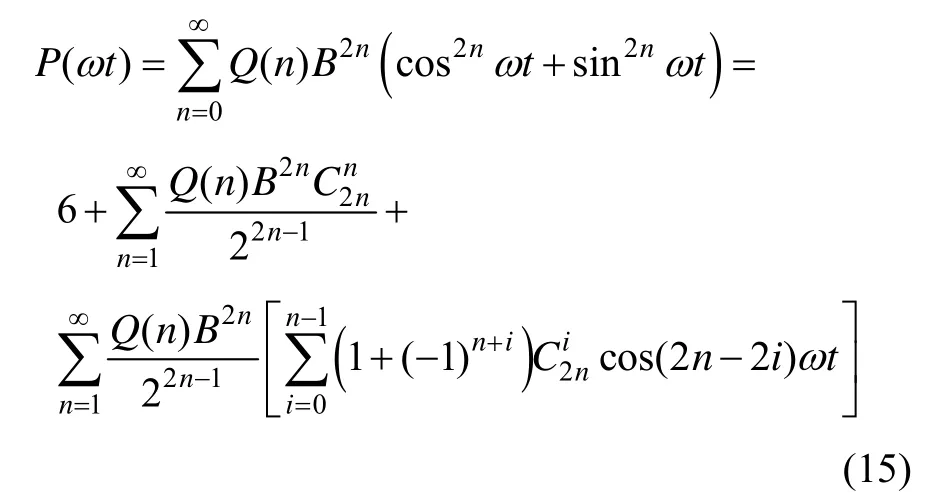
令

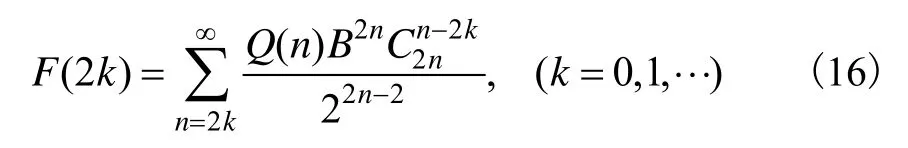
当k=0时，

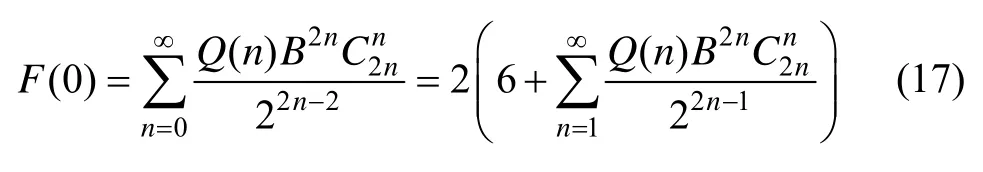
式(15)变为：

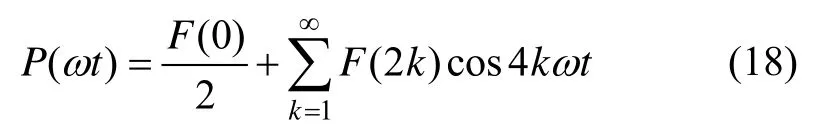
将上述式(18)代入式(12)，整理得：

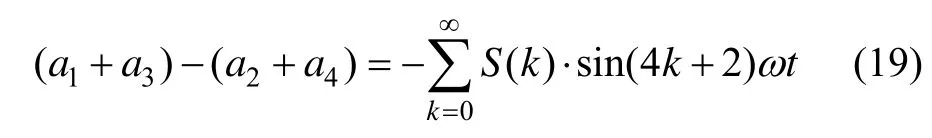
式中，

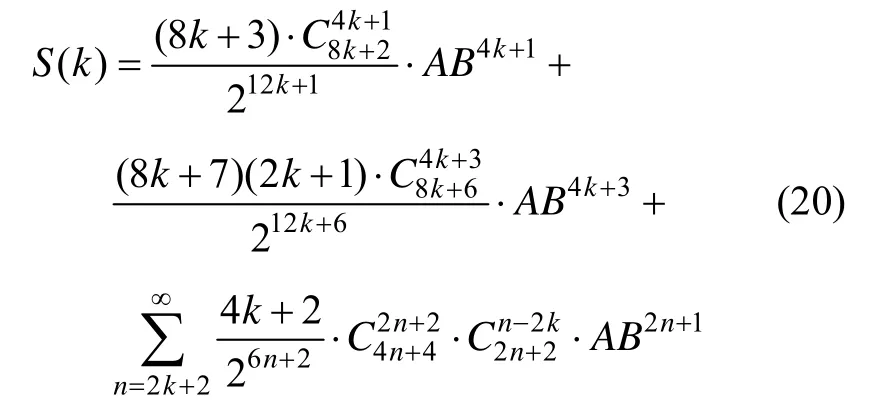
令(k=0,1,2,3)，得到前4项倍频分量sin2ω t、sin6ω t、sin10ω t和sin14ω t的系数，分别为：

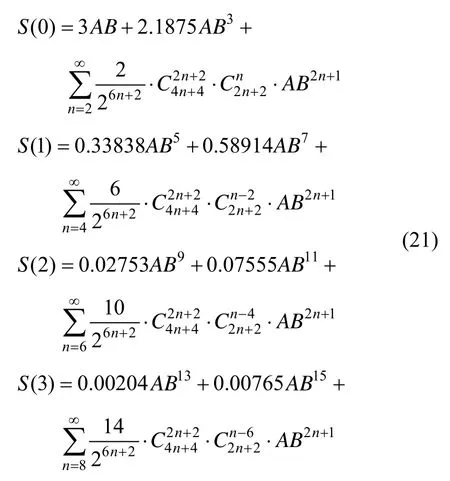
根据Stirling公式，当（n→∞）时，阶乘n!可以用幂函数近似，即：

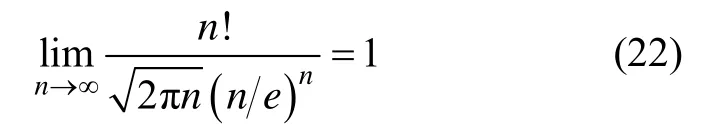
当（n→∞）时，S(0)有如下近似表达式

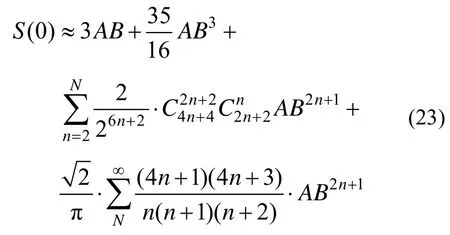
类似地，可以得到如S(1)、S(2)和S(3)等其它系数的近似计算式。计算各个系数的具体值，即各次谐波分量的幅值大小，列于表1所示。

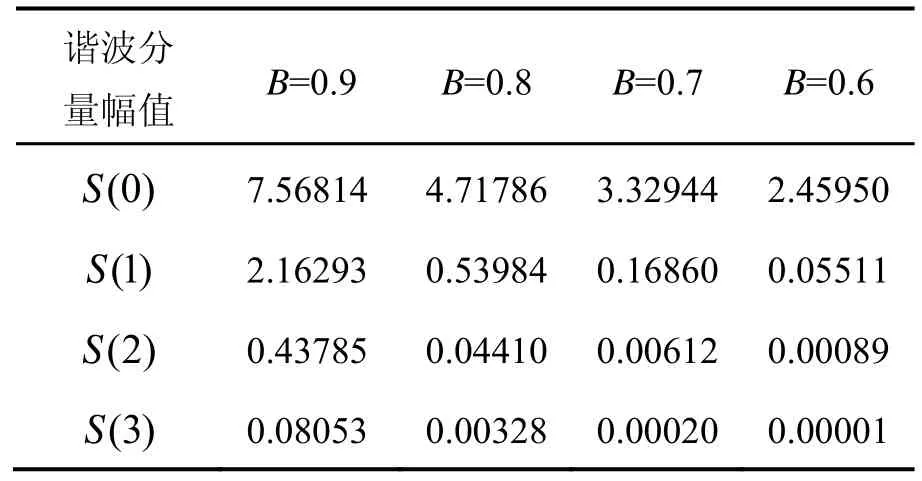
表1 S(k)系数的具体值Tab.1 Value ofS(k)coefficient

2 频域分析

通过表1可以发现，重力梯度仪输出中的各次谐波的幅值即系数S(k)是随着B取值不同而变化的。引入‘质点与圆心距离-圆盘半径比’，那么式(8)变为：

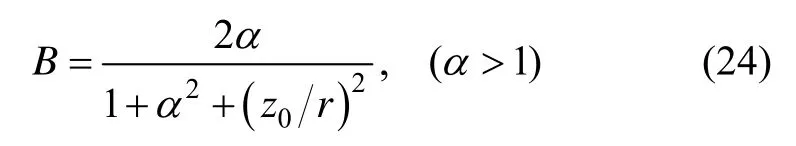
以α为横坐标，S(k)为纵坐标，4加速度计输出中前四项频率分量的幅值随α的变化关系，如图3所示。图中相同α对应sin2tω、sin6tω、sin10tω和sin14tω的幅值依次降低，说明 2倍频率信号始终占据重力梯度仪输出中的主要成分。输出中的谐波分量频率越高幅值越小，因此在分析中只要考虑前几项谐波的影响即可。

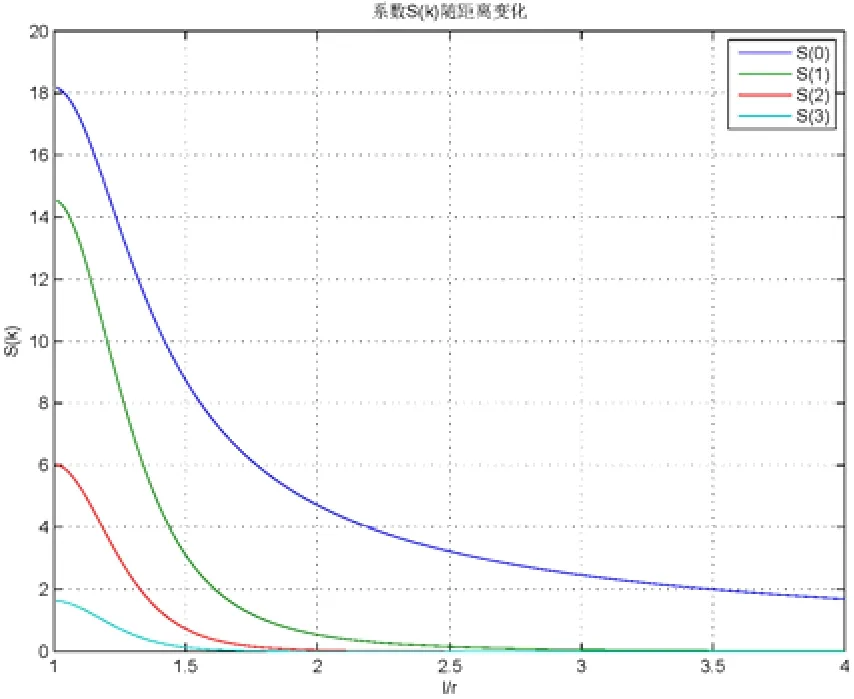
图3 输出中前4项频率分量的幅值随α的变化关系.Fig.3 The relationship between the top 4 frequency components’ amplitudes withα.

同时注意到，当α＜1.5左右时，其它谐波分量的幅值均有大幅提高。随着α的减小，即质点M距离圆盘中心越来越近，各次谐波分量相对于信号也变得越来越大，并不可被忽略。

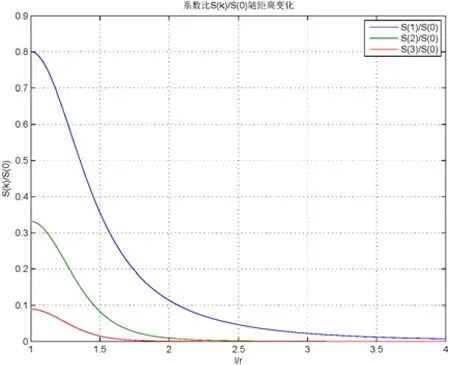
图4 前3项谐波相对于2倍频信号随α的变化关系.Fig.4 The relationship between the first 3 harmonic components’ amplitudes relative to signal withα.

以α为横坐标，为纵坐标，研究 4加速度计输出中前3项谐波分量的幅值相对于2倍频信号随α的变化关系，如图4所示。质点M贴近圆盘边缘的极端情况下，sin6tω、sin10tω和sin14tω的谐波分量的幅值分别达到了sin2tω信号幅值的约80%、33%和9%。因此，必须针对重力梯度仪的输出信号特点，设计合适的低通滤波器以滤除谐波分量。

3 结 论

通过对 4加速度计输出在频域展开可以发现，4加速度计输出在频域由倍频分量构成，相邻分量之间的频差为2ω/π，即圆盘旋转频率的4倍，谐波分量不可被忽略。为了得到重力梯度值，设计合适的低通滤波器，以对信号之外的谐波分量进行衰减。

（References）：

[1]Dransfield M H,Christensen A N.Performance of airborne gravity gradiometers[J].The Leading Edge,2013,32(8):908-922.

[2]DiFrancesco D,Grierson A,Kaputa D,et al.Gravity gradiometer systems–advances and challenges[J].Geophysical Prospecting,2009,57(4): 615-623.

[3]DiFrancesco D,Martin L.The growth of airborne gravity gradiometry–and challenges for the future[C]//12th International Congress of the Brazilian Geophysical Society.2011.

[4]DiFrancesco D,Meyer T,Christensen A,et al.Gravity gradiometry–today and tomorrow[C]//11th SAGA Biennial Technical Meeting and Exhibition.2009.

[5]李海兵，蔡体菁.旋转加速度计重力梯度仪误差分析[J].中国惯性技术学报，2009，17(5)：525-528.LI Hai-bing,CAI Ti-jing.Error analysis on gravity gradiometer of rotating accelerometer[J].Journal of Chinese Inertial Technology,2009,17(5): 525-528.

[6]杨功流，刘洋希，李晓平.重力梯度仪加速度计控制回路分析与设计[J].中国惯性技术学报，2009，17(2)：145-152.YANG Gong-liu,LIU Yang-xi,LI Xiao-ping.Analysis and design on control loops of gravity gradiometer accelerometer[J].Journal of Chinese Inertial Technology,2009,17(2): 145-152.

[7]涂良成，李祝，伍文杰，等.航空重力与重力梯度测量对惯性稳定平台的需求分析[J].中国惯性技术学报，2012，20(01)：18-23.TU Liang-cheng,LI Zhu,WU Wen-jie,et al.Requirement analysis of moving-base platform in airbrone gravimetry and gravity gradiometry[J].Journal of Chinese Inertial Technology,2012,20(01): 18-23.

[8]Jeffrey A,Zwillinger D.Table of Integrals,Series,and Products[M].7th ed.New York: Academic Press,2007.

Frequency domain analysis on superposed signal of four rotating accelerometers about proof mass

DING Hao,CAI Ti-jing
(School Of Instrument Science & Engineering,Southeast University,Nanjing 210096,China)

The gravity gradient can be obtained from the output signals of four symmetrically mounted high-precision accelerometers on a rotating disk.For this four rotating accelerometers,the frequency domain characteristics of the superposed signal about proof mass are studied.The deduced expressions of frequency domain prove that certain higher harmonic components exist in addition to the signal,and the harmonic frequency offset is four times that of the disc rotation frequency,while the harmonic frequency is 6 times,10 times or 14 times,etc.,respectively.Then the approximate calculation method of each harmonic coefficient is given by using the stirling formula.The numerical simulation results show that,the closer the distance between the proof mass and the disc,the greater the amplitude of harmonic component.

gravity gradiometer; rotating accelerometer; proof mass; frequency domain analysis; harmonic;filter design.

U666.1

：A

1005-6734(2014)02-0167-05

10.13695/j.cnki.12-1222/o3.2014.02.005

2013-11-1；

：2014-03-08

“十二五”863主题项目（2011AA060501）

丁昊（1979—），男，博士研究生，从事精密仪器研究。E-mail：dinghao32901@126.com

联 系 人：蔡体菁（1961—），男，教授，博士生导师。E-mail：caitij@seu.edu.cn