大口径快摆镜机构系统辨识及控制参数优化

史少龙，尹达一，龚惠兴

（1. 中国科学院 上海技术物理研究所，上海 200083；2.中国科学院大学，北京 100039）

大口径快摆镜机构系统辨识及控制参数优化

史少龙1,2，尹达一1，龚惠兴1

（1. 中国科学院 上海技术物理研究所，上海 200083；2.中国科学院大学，北京 100039）

为了满足光学精密工程中光束方向控制执行机构-大口径快摆镜机构(LAFSM)高精度的控制要求，对LAFSM结构特性、系统辨识方法以及其实验平台构建、控制器参数优化等进行了研究。首先详细分析了LAFSM系统组成、结构及电学特性，推导出系统模型的结构类型，建立了LAFSM系统辨识方法，搭建了实验平台。此方法剔除了数据采集系统本身对系统辨识的影响，有效减弱了背景噪声的干扰，得出了精确的系统数学模型，在小于40 Hz范围内，幅频特性误差小于0.8 dB，相频误差小于1°。根据精确的数学模型设计了PID控制器，采用广义Hermite-Biehler定理计算出使LAFSM闭环系统稳定的比例、积分、微分系数的取值范围，运用遗传算法对PID参数进行整定和优化，消除系统的振动、超调及稳态误差，使响应时间控制在0.2 s以内，系统稳态误差为0。实验和仿真证明，本系统辨识方法可靠可行，精度高；控制器参数优化方法快速高效，控制效果良好。

大口径快摆镜机构；系统辨识；控制参数优化；遗传算法

随着光学精密工程的发展，快摆镜（Fast Steering Mirror，FSM）作为目标和接收器之间控制光束方向的反射镜装置被广泛应用于天文望远镜、空间激光通信、空间精密稳像和自适应光学等光学系统中[1]。随着天文望远镜口径和视场的增加，FSM口径也越来越大。多国合作研制的南部天体物理学研究望远镜(Southern Astrophysical Research Telescope，SOAR)中的第三镜为FSM，口径为650 mm×470 mm，音圈电机驱动，行程±20″，工作带宽50 Hz（＜0.1″)，5 Hz（＜1″)，分辨率0.03″[2-3]。 詹姆斯韦伯天文望远镜（James Webb Space Telescope，JWST）的FSM位于第三镜和科学仪器焦面之间，口径 170 mm，惯量为0.0014 kg· m2，位置分辨率为0.002″，闭环控制频率为2 Hz[4]。同温层红外天文台（Stratospheric Observatory for Infrared Astronomy，SOFIA）的FSM是其次镜，直径 350 mm，双曲面，对镜片背部结构进行了优化设计后，槽腔壁厚仅为2 mm，镜片本征频率为2 kHz，重量仅为2.2 kg，工作频率为35 Hz[5]。

LAFSM能够在小范围内高精度地调整光线方向，其控制器系统的设计和研究成为研究的热点。在控制系统设计过程中，控制器结构和控制参数的确定方法有工程调试方法和理论设计方法。工程调试方法不需要对控制对象建模，但存在调试困难、工作量大、不易得到最佳效果等缺点，且有调试不当损坏被控对象的风险。FSM作为控制光束方向的精密执行机构，其行程小，角分辨率高，需要很高的控制精度，工程调试方法已经不适合如此高的要求，必须考虑采用精度更高、更有效率的理论设计方法。被控对象精确的数学模型是进行控制系统理论设计的基础。建立被控对象数学模型的方法有两种：解析法和系统辨识法。当被控对象较简单时，可应用解析的方法根据有关知识建立对象的机理模型，并达到较高精度。考虑到FSM结构复杂，各组成部件参数测量困难且测量结果可信度低，建立其精确机理模型十分困难，需要通过设计实验获得对象的输入输出数据，然后运用系统辨识知识得到精确地FSM系统模型，最后根据辨识出的FSM数学模型，对控制器参数进行整定和优化，从而实现设计目标。

1 系统辨识及控制参数优化流程

系统辨识就是一种从观测到的含有噪声的输入输出数据中提取数学模型的方法，而PID控制器参数优化是在已知被控对象精确的数学模型的前提下，求取使闭环系统稳定的比例、积分、微分参数范围，然后运用参数优化的方法对参数进行优化，寻找最优解。具体的方法和流程如下：

1）系统模型结构辨识。首先详细分析LAFSM的驱动方式和支撑结构，根据物理方程推导系统模型的结构组成。

2）系统模型辨识实验设计。设计LAFSM的激励驱动模块和输出数采模块，通过实验方法获得特定输入激励条件下对应的输出数据。

3）模型参数辨识。首先对获得的输入输出数据进行最小二乘拟合得到在各个频率点上输入输出的幅度和相位，然后根据系统的模型结构，辨识模型参数。

4）模型检验。检验辨识模型的频率特性和实测模型的频率特性的差异度，作为系统辨识精度高低的评判标准。

5）PID稳定参数范围求取。采用广义 Hermite-Biehler定理求取PID稳定参数的取值范围，为参数整定和优化建立条件。

6）PID参数整定优化。应用遗传算法[6-8]对 PID参数进行整定和优化。

以上流程获得的优化控制参数需带入到实际控制系统中进行进一步微调。

2 系统辨识实验平台的设计及实现

2.1 系统模型结构辨识

1）大口径快摆镜模型结构

LAFSM由底座、反射镜、驱动器以及柔性弹性支撑机构组成。LAFSM 系统按其驱动模式和自由度可以分为：单驱动单自由度，双驱动器单自由度，三驱动器双自由度，三驱动器三自由度和四驱动器双自由度几种。

系统所用的LAFSM，口径500 mm×700 mm，短轴惯量0.176 kg·m2，长轴惯量0.276 kg·m2，系统需要有双自由度摆动（tip/tilt），采用四压电陶瓷促动器（Piezoelectric Actuators，PZT）驱动结构，如图1所示。

两对PZT分别成90度空间排列，每一对作为一个推拉模块被驱动。四个PZT有一个桥结构连通，并由一个固定电压和两个可变电压驱动。因为每一对PZT都是平行于正交偏转轴xθ和yθ因此不再需要并行转换。

LAFSM、PZT、柔性支撑机构的机械部分在一维情况下可视为一个单自由度扭振系统。设：LAFSM单轴转动惯量为J，转动角度为θ，粘性阻尼系数为C，转动半径为R，压电陶瓷最大行程为Lmax，最大工作电压为Umax，实际工作电压为U，弹簧系数为ξ。LAFSM在工作过程中，PZT的驱动力矩Te，阻尼力矩Td，惯性力矩，镜面采用的柔性铰链，弹性力矩为Tf。根据力矩平衡，建立系统运动微分方程为：

柔性铰链的弹性系数为，则弹性力矩为：

图1 LAFSM结构图Fig.1 Structure of LAFSM

阻尼力矩的产生和特性实际上很复杂，为了简化模型将其考虑为粘性阻尼。粘性阻尼的特点是阻尼力的大小与速度成正比，方向与速度相反。阻尼力矩表示为阻尼系数与角速度乘积的形式为：

PZT驱动力矩：

式(4)中F为PZT的推力，即：

综上，将式(2)～(5)带入式(1)得：

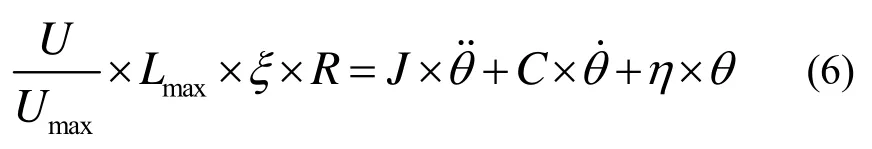
由此可得LAFSM的机电动力学方程为：

经拉普拉斯变换，LAFSM的s域方程为：

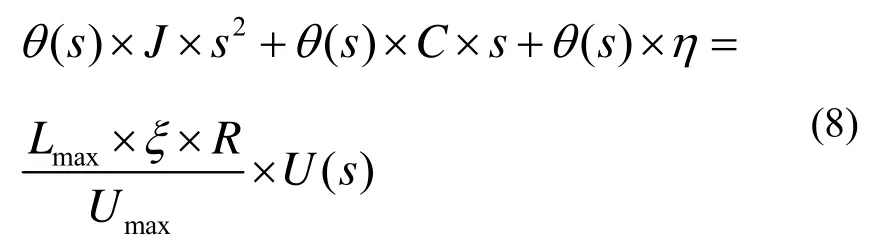
LAFSM的频域传递函数为：

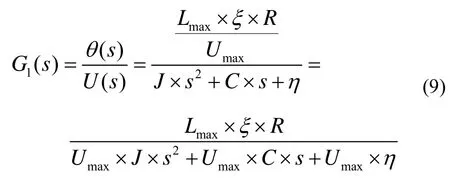
2）压电陶瓷驱动器模型结构

数字模拟转换模块（Digital-to-Analog Converter,DAC）输出的控制电压经过低通滤波器后，采用高压功率放大器放大,驱动 PZT。低通滤波器模型可用一阶惯性环节近似，而高压功率放大器可用比例环节近似，设放大倍数为K1。则PZT驱动模块的传递函数可以等效为：

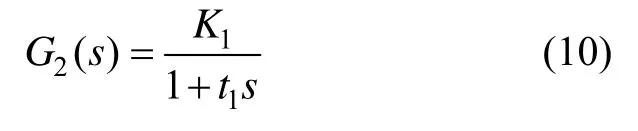
3）检测模块模型结构

电容传感器是一个高带宽的高精度的位移测量器件，可用一个比例环节近似。在电容传感器信号调理电路中包含有滤除高频噪声的低通滤波器，因此整个位置检测模块传递函数为：

综上，LAFSM的系统传递函数可以写成一个二阶振荡环节和两个一阶惯性环节的串联。如式(12)所示：

由于系统辨识实验用的模拟数字/数字模拟转换器(Analog-to-Digital Converter/Digital-to-Analog Converter，ADC/DAC)与实际控制系统中所用的ADC/ DAC，型号和工作原理有所不同，导致造成的延迟也有所不同。当两者延迟量可以相比拟时，系统辨识的模型结构为式(12)所示；当延迟量相差很大时，需要在设计实验时剔除ADC/DAC环节对系统辨识的影响。详见2.2节实验设计。

本辨识实验所用ADC/DAC为24位delta sigma型，比实际控制系统中ADC/DAC的延迟量大很多，所以 LAFSM 系统模型可以表述为一个二阶振荡环节、一个一阶惯性环节和一个比例环节的串联，即：

2.2 级联积分梳状滤波器

在模型参数辨识前需获得 LAFSM系统的输入输出数据，需要设计数据采集系统，确定激励信号形式以及采样时间等。

数据采集系统选用 NI公司的实时控制器PXIe-8180，2输入2输出动态信号采集卡PXI-4461，PI公司的 D-100.00电容传感器，电容信号调理器E-509-C3A组成，实验框图如图2所示。

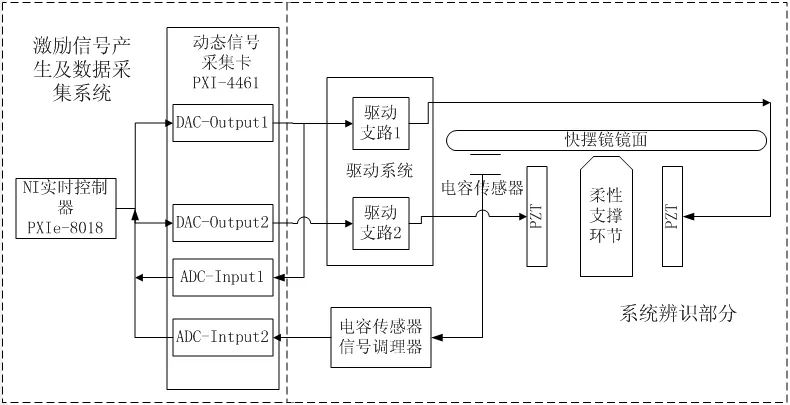
图2 系统辨识实验平台框图Fig.2 Block diagram of the experimental platform for system identification

动态信号采集卡PXI-4461为24位delta sigma 转换器，能以204.8k采样率（Samples Per Second，SPS）对92 kHz带宽内的模拟信号进行动态范围接近120 dB的连续采样。它的2个DA输出通道可生成高达92 kHz的频率模拟信号，是正弦扫频等混合器控制和激发响应测试的理想之选。PXI-4461内部有抗混叠滤波器，在不同的采样率下有不同的延迟，且延迟影响需要考虑。例如当采样率为10kSPS时，ADC/DAC的延迟为39.75个采样点。由于此延迟较实际控制系统中 ADC/DAC延迟大很多，根据2.1节所述，在系统辨识过程中要予以剔除。实验设计过程中，设计一路驱动信号经DACOutput1输出后，一支路输入到驱动系统驱动LAFSM，一支路直接回到动态信号采集卡的 ADC端口ADC-Input1，经 ADC采集后作为系统输入激励信号,如图2所示。由于PXI-4461各个通道在采样率一致的情况下延迟相同，所以可以剔除 ADC/DAC延迟对系统辨识的影响。

辨识过程要求激励信号对过程的“静扰动”要小，即正、负向扰动要尽量均等，而且激励信号的幅度不宜过大，以免被控对象进入非线性工作区。考虑到外界背景噪声的影响，激励信号幅值也不能取太小，否则将影响辨识的精度。

采样频率选择和实际控制系统的采样频率保持一致，满足奈奎斯特采样定理。

2.3 模型参数辨识

经典的系统辨识方法有：阶跃响应法、脉冲响应法、频率响应法、相关分析法、谱分析法、最小二乘法和极大似然法等。

系统采用频率测试法。基本思想是通过扫频测试得到FSM系统的幅频响应特性和相频响应特性，然后写出开环传递函数频率特性的复数表示，最后根据第3.1节得到的模型结构通过非线性最小二乘拟合得到模型参数。

激励信号为正弦信号：

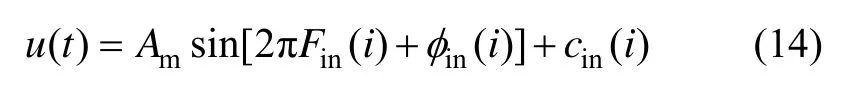
系统工作在线性区的情况下，系统的输出信号也应为相同频率的正弦信号：

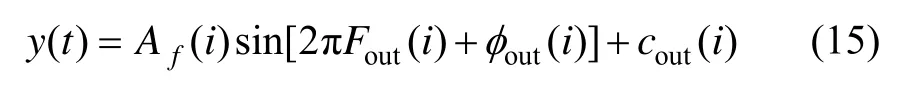
Fin为一维数组，对应起始频率为5 Hz，终止频率为180 Hz，步长为5 Hz的一组频率点；φin、φout分别为输入输出信号不同频率下的初始相位；而cin、cout为不同频率下输入输出信号的直流偏置。

设置数据采集系统的采样频率为10 kSps，分别用幅度为0.5 V，频率为5 Hz,10 Hz,15 Hz,…,180 Hz的正弦信号驱动LAFSM，在每个频率点下等系统稳定后，采集输入输出信号，采样数据为10k个点。

由于实验环境不可避免地存在背景噪声，而LAFSM本身口径大，偏转行程短，分辨率高，对环境噪声非常敏感，再加上本实验中输入信号幅度较小，更容易受到环境噪声的影响，所以必须对环境噪声进行分析。

图3 背景噪声Fig.3 Background noise

采集LAFSM无激励信号时的背景噪声信号，其时域波形图如图 3(a)，对背景噪声进行频域分析得到其幅频曲线和功率密度谱如图3(b)和图3(c)所示。有图(a)可知，噪声峰峰值在0.08 V左右，频谱分析知背景噪声主要集中在3 Hz和22 Hz两个频率点上。

对测量得到的输入、输出波形按式(14)和式(15)进行最小二乘曲线拟合，得到各个频率点上的输入输出信号幅值Am、Af和相位、φout，这样可以有效减小背景噪声的影响，提高辨识精度。每个频率点上的幅频和相频响应可以根据实测值由式(16)和式(17)计算得到：

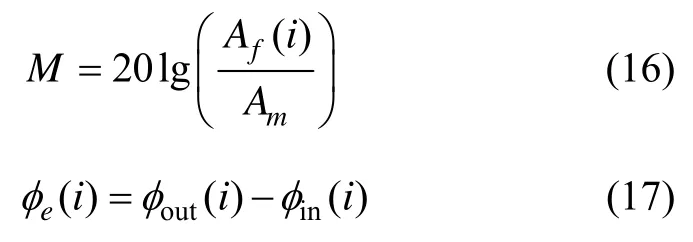
求出LAFSM系统的实测幅频和相频响应后，以式(13)作为模型结构，采用非线性最小二乘法拟合模型参数，确定其传递函数为：

2.4 模型检验

图4为实测LAFSM和拟合得到的系统模型的频率特性曲线。

根据3.3节获得的辨识参数和数据对模型进行检验：在小于40 Hz范围内，幅频特性误差小于0.8 dB，相频小于1°。而在55 Hz和175 Hz附近，存在两个机械谐振环节，经初步分析是由LAFSM的机械结构及其刚度决定的。

图4 实测频率特性曲线和辨识系统频率特性曲线比较Fig.4 Comparison between characteristic cures of measured frequency and identified frequency

3 控制参数整定与优化

PID控制因其结构简单、鲁棒性好被广泛适用于工业控制领域。设计PID控制器，其传递函数可表示为：

由于LAFSM有很高的控制精度且响应迅速，所以必须对PID参数进行合理的整定和优化。常用的方法有最优控制法、单纯形法、专家整定法、继电反馈法等，这些算法都有一定的局限性，比如单纯形法对初值比较敏感，容易陷入局部最优解。专家整定法需要太多的被控对象经验。经过对比选用遗传算法来进行参数优化，该方法是一种不需要任何初始信息便可寻求全局最优解的、高效的优化组合方法。

在运用遗传算法进行参数优化前，必须确定使闭环系统稳定的比例、积分、微分三参数的取值范围，否则超出系统稳定参数范围，造成系统不收敛。对比了 M.T.Söylemez等在文献[9]提出的理论以及Hermite-Biehler定理和广义Hermite-Biehler定理[10]，选用操作较为简便的后者计算出三个参数的取值范围为：。

遗传算法优化PID控制参数流程如图5所示。

图5 遗传算法流程Fig.5 Flowchart of genetic algorithm

优化出的 PID参数为：Kp=0.024，Kd=0，Ki=49.5797。从优化结果可以看出，PI控制器更适合LAFSM系统的控制。优化前后系统的阶跃响应分别如图6所示。由图6可知，LAFSM系统加入PI控制器后，消除了FSM系统开环阶跃响应的过冲、振荡以及稳态误差，并且能够迅速稳定，达到稳态值，响应时间在0.2 s以内，稳态误差为0。

图6 参数整定前后阶跃响应比较Fig.6 Comparison of step responses before and after parameter tuning

4 结 论

运用理论建模和实验建模相结合的方法对LAFSM 系统进行系统辨识，对比实测频率响应和辨识模型频率响应曲线，二者相符度很高。根据精确的LAFSM数学模型，设计了PID控制器。首先求得使闭环系统稳定的PID控制参数取值范围后，运用遗传算法对PID参数进行整定和优化，最终消除大口径快摆镜闭环系统的振荡、超调以及稳态误差，且响应时间控制在0.2 s以内。结果证明，提出的大口径快摆镜系统辨识方法可靠可行，精度高；PID控制器参数优化方法快速高效，控制效果良好。LAFSM系统辨识不仅能够为控制器设计提供精确的数学模型，而且可以作为评价LAFSM机械结构设计的有效依据。

研究中发现，LAFSM的结构特性和材料刚性以及外部背景噪声均会对系统辨识的精度产生影响，需要在今后的工作中加以更多关注并进行进一步的研究。

（References）：

[1]徐飞飞，纪明，赵创社.快速偏转反射镜研究现状及关键技术[J].应用光学，2010，31(5)：847-850.XU Fei-fei,JI Ming,ZHAO Chuang-She.Status of fast steering mirror[J].Journal of Applied Optics,2010,31(5):847-850.

[2]赵碧杉.大口径快摆机构高精度控制技术研究[D].北京：中国科学院，2013.ZHAO Bi-shan.Research on high-precision control technology of large caliber fast steering mirror[D].Shanghai: Shanghai Institute of Technical Physics of the Chinese Academy of Science,2013.

[3]Warner M,Heathcote S,Schumacher G,et al .Upgrading the controller of the fast tip-tilt tertiary mirror for the SOAR telescope[C]//Proc.SPIE 7739,Modern Technologies in Space- and Ground-based Telescopes and Instrumentation.2010: 77393D.

[4]Meza L,Tung F,Anandakrishnan S,et al.Line of sight stabilization for the james webb space telescope[C]// 28th Annual AAS Rocky Mountain Guidance and Control Conference.2005,121: 17-30.

[5]Reinacher A,Onillon E,Roeser H P.Improvement of the SOFIA secondary mirror controller[C]//Proc.SPIE 7733,Ground-based and Airborne Telescopes III.2010: 77330Q.

[6]Guo Pengfei.The enhanced genetic algorithms for the optimization design[C]//2010 3rd International Conference on Biomedical Engineering and Informatics.2010: 2990-2994.

[7]王茂林.改进遗传算法及其在 PID控制器参数优化中的应用[D].吉林：吉林大学，2011.WANG Mao-lin.Improved genetic algorithm and its application in PID controller parameter optimization[D].Changchun: Jilin University,2011.

[8]向红标，裘祖荣，李醒飞，等.精密实验平台的非线性摩擦建模与补偿[J].光学精密工程，2010，18(5)：1119-1127.XIANG Hong-biao,QIU Zu-rong,LI Xing-fei,et al.Nonlinear friction modeling and compensation of highprecision experimental platforms[J].Optics and Precision Engineering,2010,18(5): 1119-1127.

[9]Turan M,Nevra S.Calculation of All H∞robust stabilizing gains for SISO LTI systems[C]//Proceedings of the 17th World Congress.The International Federation of Automatic Control.Seoul,Korea,July 6-11,2008.

[10]Elmadssia S,Saadaoui K,Benrejeb M.PI Controller design for time delay systems using an extension of the Hermite-Biehler theorem[J].Journal of Industrial Engineering,2013: 813037-813043.

Large-aperture fast steering mirror system identification and controller parameter optimization

SHI Shao-long1,2,YIN Da-yi1,GONG Hui-xing1
(1.Shanghai Institute of Technical Physics of the Chinese Academy of Sciences,Shanghai 200083,China;2.University of Chinese Academy of Sciences,Beijing 100039,China)

In order to meet the precision control requirements of large-aperture fast steering mirror mechanism(LAFSM) in optics and precision,the structural characteristics,experiment platform and control method of LAFSM and system identification methods are studied.Firstly,the support structures of the LAFSM,the structural and electrical properties of various components are analyzed.Then the structure of the model in theory is derived.Based on this,the system identification method of the LAFSM and an experiment platform are designed.This method excludes the effect of data acquisition system upon system identification,and the background noise interferences are weakened to a certain extent.Then the precise mathematical model of the LAFSM is derived.In 40 Hz range,the amplitude-frequency characteristic error is less than 0.8 dB,and the phase-frequency error is less than 1°.After that,the PID controller design is completed.The range of proportional,integral and differential coefficients,which make the closed-loop system stable,are calculated based on Hermite-Biehler theorem.After all,the PID parameters are tuned and optimized by using the genetic algorithm.It is proved that the controller significantly eliminate the vibration,overshoot and steady-state error,the response time is less than 0.2 s,and the system steady-state error is 0.Experiments and simulations show that this system identification method is stable,reliable,and high precision.The proposed optimization method of controller parameters is fast and efficient.

large-aperture fast steering mirror; system identification; PID tuning; genetic algorithm

TN247

：A

1005-6734(2014)02-0161-06

10.13695/j.cnki.12-1222/o3.2014.02.004

2013-11-20；

：2014-03-04

国家自然科学基金资助项目（40776100）

史少龙（1985—），男，博士研究生，从事空间高精度稳像控制技术方面的研究。Email：s_s_l@163.com

联 系 人：龚惠兴（1940—）男，中国工程院院士，博士生导师。Email：hxgong@mail.sitp.ac.cn