随机激励下基于ICA的结构模态参数识别

静 行，刘真真，原 方

（河南工业大学 土木建筑学院，郑州450001）

随机激励下基于ICA的结构模态参数识别

静 行，刘真真，原 方

（河南工业大学 土木建筑学院，郑州450001）

简要介绍独立分量分析(ICA)的基本原理，提出将ICA方法与随机减量法(RDT)结合起来用于随机激励下结构的模态参数识别。结合数值仿真算例和振动试验分析，验证所提出方法用于随机激励下结构模态参数识别的有效性。结果表明，ICA可以准确地从结构随机振动响应信号中分离出各源信号，并同时估计出各阶模态振型向量，源信号与结构模态坐标存在一一对应关系，再结合随机减量法和单模态识别法可识别各阶模态的频率和阻尼比。该方法仅利用振动系统的输出响应进行分析，适用于随机激励下结构的工作模态参数识别。

振动与波；模态参数识别；独立分量分析；随机激励；信号处理

模态参数识别的主要任务是从测试所得的数据中，确定振动系统的模态参数，其中包括模态的固有频率、阻尼比和模态振型等，这些动力特性参数可以作为结构健康诊断、实时监测、结构有限元模型修正的评定标准和基础[1]。因此，模态参数识别具有重要的现实意义。

独立分量分析[2](Independent Component Analysis，ICA)是上世纪90年代后期伴随着盲源分离问题而发展起来的一种统计信号处理和数据分析方法。目前，ICA方法已经成功应用于结构工程领域，在工程结构振动信号分析、结构损伤识别及模态分析等方面取得了突破性的进展。如文献[3]提出了基于独立分量分析的振动信号降噪方法；文献[4]提出了利用ICA方法来有效实现结构损伤识别；文献[5]将ICA用于结构的模态分析，从结构的自由振动响应中准确提取模态振型和模态坐标。然而目前关于ICA在随机激励下结构模态分析中应用的研究鲜有报道。

本文将在ICA的基础上尝试一种新思路，即将ICA与随机减量法（RDT）结合起来用于随机激励下结构的模态参数识别。在简要介绍ICA的基本原理后，探讨了随机激励下多自由度系统动力响应模态提取与独立分量分析之间的关系，进而提出随机激励下基于ICA的结构模态参数识别方法与流程。最后，结合数值仿真算例和振动试验分析，验证了所提出方法用于随机激励下结构模态参数识别的有效性。

1 独立分量分析(ICA)

1.1 ICA模型

设有n个信号源和m个传感器，且测量信号和源信号之间关系式为：

s为未知的n维源信号向量，s=[s1，s2，···，sn]T；x为m维观测信号向量，x=[x1，x2，···，xm]T；A为未知的m×n的混合矩阵；观测信号x为未知信源s的线性组合。

根据上述，ICA问题可以描述为：在仅能观测到信号x的情况下，同时估计出混合矩阵A和源信号s，即求解出一个解混矩阵W，并把W对混合信号矢量x的线性变换y=Wx作为源信号s的估计，进而对W求逆就能得到矩阵A的估计。

由于对源信号和混合矩阵无任何先验知识可以利用，当把一组混合信号分解成若干独立成分时，分解结果肯定存在多解。因此为了保证上述ICA模型可以被估计，通常需要对源信号以及混合矩阵作出相应假设[2,6]：

(1)源信号的各个分量之间是相互统计独立的；

(2)源信号的各分量必须是非高斯信号或最多只能有一个是高斯信号；

(3)源信号的分量个数m小于观测信号分量的个数n。也就是说，由n个观测信号最多能分解出n个源信号分量。同时假定混合矩阵A是可逆的。这些假定在分析某些特定类型信号时还可适当放宽。例如源信号是时间信号时，各分量之间相互统计独立的假定就可放宽至相互不相关[6]。

另外需要说明的是，根据ICA模型的描述，分离矩阵W不是A的求逆过程，利用ICA得到的源信号只是真实源信号的最优估计，它们之间可能是某种比例关系，也就是一个信号可能等于另一个信号乘以一个常数，而且目前ICA也无法决定分离出源信号的顺序。然而在实际应用中，这些不确定性都是能够接受的。

1.2 基于负熵的固定点算法

ICA方法的问题核心就是寻找一个可以判别分离结果独立性的准则，以及相应的分离算法。根据中心极值定理，非高斯随机变量之和比原变量更接近高斯分布。对ICA模型来说,观测信号是多个独立源信号的线性混合,故观测信号较各独立源信号更接近高斯分布。因此可以利用非高斯性来判别分离结果之间的相互独立性，当各分离结果的非高斯性达到最强时，表明已完成对各独立分量的分离。

基于负熵的快速固定点算法(Fast ICA)就是用负熵来度量非高斯性从而寻找极大化非高斯性的不动点迭代方法。Fast ICA算法步骤可总结如下[2]：

（1）对观测信号进行中心化；

（2）白化处理，得到z；

（3）任选一个初始化向量w（w为单位范数）；

（4）由牛顿迭代定理，令

（5）归一化：w=w+/‖w+‖；

（6）如不收敛返回步骤（4）。

其中g′为近似计算负熵方法中的非二次型函数的导数。

以上仅探讨了如何提取单个独立分量。如果要提取多个源信号，则需多次重复运行上述算法，通过取不同的w值以提取出多个信源。为防止收敛相同，返回步骤（4）之前需进行正交化处理并去除已经提取过的分量。如此直至分离出所有的独立分量。

2 随机减量法(RDT)

随机减量法（RDT）是指从线性振动系统的一个或多个平稳随机响应样本中提取该系统自由振动响应的数据处理方法。其原理叙述如下[7,8]。

对于线性单自由度系统，在任意激励下某测点的受迫振动响应可表示为

式中D(t)是初始位移为1、初始速度为0的系统自由振动响应；V(t)是初始位移为0、初始速度为1的系统自由振动响应；h(t)是系统单位脉冲响应函数；f(t)为外部激励；x(0)和x˙(0)分别为系统初始位移和初始速度。

选取一个适当的振幅值A去截取系统的随机响应信号x(t)，则水平线x=A与响应信号x(t)的交点所对应的时刻为ti(i=1,2,…,n)。对于自ti时刻开始的响应x(t-ti)可以表示为：

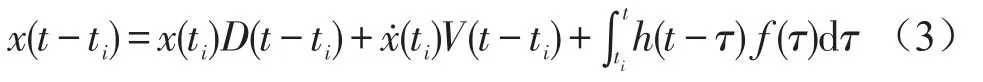
将x(t-ti)的时间起始点ti移至坐标原点，可获得一系列随机过程的子样本函数yi(t)(i=1,2,…,n)：

取yi(t)的统计平均为

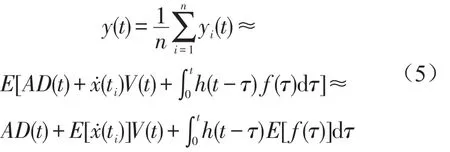
若激励f(t)是均值为0的平稳随机过程，则系统的振动响应x(t)和同样是均值为0的平稳随机过程，进而E[f(t)]=0、，则

由此得到了初始位移为A初始速度为0的自由振动响应信号。

3 模态参数识别方法

任一n个自由度结构体系的振动运动方程为：

式中M、C和K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵；x、x˙和¨分别为结构的位移、速度和加速度向量；f(t)为外荷载向量。对于小阻尼的一般工程结构，其位移响应可以用模态坐标表示为

其中ψi为第i阶模态振型向量；qi为模态坐标；Φ为振型矩阵，由n个独立的振型向量ψi组成；q(t)为模态坐标向量。

随机激励下的系统响应，一般仅能通过统计特性进行描述，而很难用时间函数进行描述。然而，对于无阻尼或阻尼较小的系统，在宽带随机激励作用下(如白噪声激励)，结构响应的模态坐标qi是以结构固有频率ωi为频率振动的，其幅值在大小值之间不规则且缓慢的变化[9,10]。只要在系统带宽上的激励谱比较平坦，且在固有频率附近没有出现高峰，就认为该结论近似成立。进而可以推测[11]

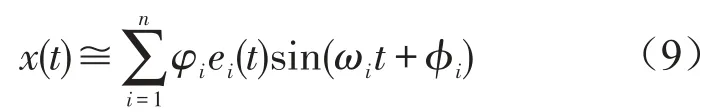
其中ei(t)是振动峰值的包络线，如果随机激励为高斯白噪声，则ei(t)将具有瑞利分布[10]。令模态坐标qi(t)≌ei(t)sin(ωit+φi)，在宽带随机激励下，结构响应的模态坐标就可看作是一种特殊的时间序列源信号，不难看出其满足ICA算法对源信号作出的相关假定。

通过以上论述，在随机激励作用下，多自由度系统动力响应的模态分解可看作是一个ICA问题。因此，在仅知道随机振动响应时域信号的情况下，可以利用ICA方法对结构进行模态参数识别。其基本思路是：

（1）通过振动试验得到结构的振动响应时域信号（如位移、速度或者是加速度信号）；

（2）利用ICA方法分析结构响应x(t)，提取出结构的各独立源信号s(t)，同时估计出混合矩阵A；

（3）混合矩阵A中包含了模态振型的信息，对矩阵A中列向量进行归一化处理，即得到了结构模态振型；

（4）对于随机响应信号，提取出的源信号也是随机过程，要先利用随机减量法去除随机部分，得到结构的自振响应信号，进而再利用单模态识别法识别出结构的自振频率和阻尼比。

4 数值算例与试验研究

4.1 数值算例

如图1所示，为一二维简支撑的三层框架结构。其中质量m1=1，m2=m3=2，刚度k1=800，k2=1 600，k3=2 400，阻尼为c1=a m1，c2=a m2，c3=a m3，这里取比例系数a=0.1。采用稳态的高斯白噪声对结构进行激励，并采用有限单元法计算每一层的结构响应。取前50 s的加速度信号为分析对象，如图2（a）所示，结构响应信号的采样频率为100 Hz。

图1 三层框架结构示意图

为了识别结构的模态参数，首先利用ICA方法对结构响应信号进行分析，提取出独立源信号（如图2（b）所示）并估计出混合矩阵A。可以看出，识别出的各独立源信号是一系列窄带的随机响应。图2（c）是与源信号相对应的Fourier变换幅值谱，可以看出，其幅值是不断变化的，而振动频率却是一定的，且频率值分布与结构的固有频率的理论解是吻合的。因此这些源信号可看作是各阶模态坐标的估计值。对混合矩阵A中列向量进行归一化处理，可以得到如图3所示的结构模态振型。可以看出，对于结构的随机响应信号，ICA方法识别出的模态振型结果是非常理想的。

对于随机响应信号，提取的源信号也是随机变量，要先利用随机减量法（RDT）去掉响应中的随机成分，提取出各阶模态的自由衰减响应信号（如图4所示）。其截取振幅值取为原始信号标准差的1.2倍，衰减长度取5 s，平均次数分别为173，498，677次。进而再利用单一模态识别法（这里采用Hilbert变换[12]）从图4所示自由衰减响应中识别出系统各阶自振频率和阻尼比，结果见表1。可以看出，ICA与RDT方法结合识别结果是非常理想的，识别出各阶自振频率的误差分别为0.182%、0.729%和2.236%。虽然识别阻尼比的结果误差相对较大，但仍在可接受的范围内。

图2 结构随机振动响应信号的独立分量分析

图3 模态振型识别结果

图4 RDT提取的各阶模态自由衰减响应曲线

4.2 框架结构振动试验

这里采用的试验数据来源于美国洛斯阿拉莫斯国家实验室的网站[13]，他们根据一三层框架结构的动力响应实验来进行结构损伤识别的研究。这里以该结构基准状态的响应数据为对象以验证上述基于ICA进行模态参数识别的有效性。图5所示为实验所用的三层框架结构以及激励装置图，实验中框架结构是由铝柱与铝板通过螺栓连接而形成的一个4自由度体系，且在结构基底设置滑行轨道限定结构只能沿图示x方向运动。在各层铝板侧边中点设置传感器，共5个通道：其中一个通道用于记录激励信号，另外4个通道用于记录结构各层及其基底的加速度响应。在分析中可以忽略结构扭转作用（测点和激励点全部位于结构中心线上，使得扭转作用产生的影响降到最小）。在结构基底侧边中点处，采用电磁激振器进行激励，激励信号为平稳随机激励（带宽在20 Hz～150 Hz之间），采样频率为320 Hz，采样时间为25.6 s，共设置8 192个采样点。

表1 自振频率和阻尼比识别结果（随机响应）

图5 三层框架结构与激励装置图

从结构第三层的加速度响应以及功率谱密度（如图6所示）可以看出，系统3阶模态均已被激发出来，对应的结构固有频率在30 Hz、54 Hz和70 Hz附近。

首先利用ICA方法分析各层的加速度响应，提取出各独立源信号以及功率谱密度（如图7所示）。显而易见，各独立源信号是以相应的固有频率振动的随机响应。虽然前两阶模态坐标相对应的独立分量含有程度不等的噪声污染，带宽相对较宽，但主要的能量仍然集中在固有频率附近。而与第3阶模态坐标相对应的独立源信号的识别结果非常理想。

同样，鉴于识别出的源信号是随机响应信号，不能直接利用Hilbert变换进行模态识别。先利用RDT法对各独立源信号进行分析，提取出各阶模态的自由衰减响应，之后再利用Hilbert变换从提取的自由衰减信号中识别出结构的固有频率和阻尼比，结果见表2。

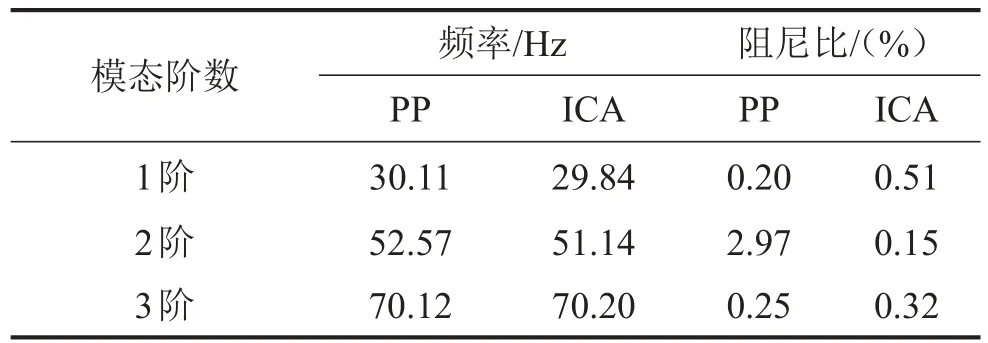
表2 框架结构固有频率和阻尼比识别结果

作为比较，这里同时给出了运用峰值提取法[14]（Peak Picking，简称PP）识别的模态参数结果，具体过程这里不再详述。从表2能够看出，ICA与峰值法识别的频率值基本是一致的。尽管两种方法识别的阻尼比差别较大，但都在合理的范围内。峰值法和ICA法识别的模态振型见图8。

图6 框架结构第三层加速度响应及其功率谱密度

图7 ICA识别的独立源信号及其功率谱密度

图8 框架结构模态振型识别结果

5 结语

本文尝试将ICA方法与随机减量法等技术结合用于随机激励下结构的模态参数识别。分析认为结构随机振动响应的振型叠加法可以看作是一个ICA问题，利用ICA方法可直接从结构的随机振动响应信号中提取出与模态坐标相对应的独立源信号并估计出相应的模态振型。由于随机振动响应信号提取的源信号也是随机过程，采用随机减量法从独立源信号中提取单模态自振响应，再通过单模态识别法识别出各阶模态频率和阻尼比。数值算例和振动试验分析结果表明了该方法用于随机激励下结构模态参数识别的可行性。该方法仅利用振动系统的输出响应进行分析，是一种时域工作模态参数识别方法，具有良好的工程应用前景。

[1]Zang C,Friswell M I,Imregun M.Structural damage detectionusingindependentcomponentanalysis[J].Structural Health Monitoring,2004,3(1)∶69-83.

[2]Hyvarinen A,Karhunen J,Oja E.独立成分分析[M].北京：电子工业出版社,2007.

[3]赵丽芝，袁海庆，杨燕.基于独立分量和扩展通道的振动信号降噪方法[J].武汉理工大学学报，2008，30(6)：79-82.

[4]曹军宏，韦灼彬.基于ICA和SVM的结构损伤识别[J].数据采集与处理，2012，27(1)：120-123.

[5]静行，袁海庆，赵毅.基于独立分量分析的结构模态参数识别[J].振动与冲击，2010，29(3)：137-141.

[6]Zhou Wenliang,Chelidze D.Blind source separation based vibration mode identification[J].Mechanical Systems and Signal Processing,2007(21)∶3072-3087

[7]彭程，张立民，李原辉，等.利用改进的EMD和随机减量法识别模态参数[J].噪声与振动控制，2011，31(5)：53-56.

[8]王佐才，任伟新.基于解析模式分解的密集工作模态参数识别[J].噪声与振动控制，2013，33(6)：18-24.

[9]李德葆，陆秋海.工程振动试验分析[M].北京：清华大学出版社，2004.

[10]克兰德尔S H.随机振动[M].北京：科学出版社，1980.

[11]Kerschen G,Poncelet F,Golinval J C.Physical interpretation of independent component analysis in structural dynamics[J].Mechanical Systems and Signal Processing, 2007(21)∶1561-1575.

[12]陈隽，徐幼麟.HHT方法在结构模态参数识别中的应用[J].振动工程学报，2003，16(3)：383-388.

[13]Elόi Figueiredo.Three-story building structure to detect nonlinear effects[EB/OL].http∶//www.lanl.gov/projects/ damage_id/index.htm,2008-10.

[14]REN W.X.,ZONG Z.H.Output-only modal parameter identification of civil engineering structures[J].Structural Engineering and Mechanics,2004,17(3-4)∶429-444.

Structural Modal Parameter Identification Based on ICAunder Random Excitation

JINGHang,LIU Zhen-zhen,YUANFang

(School of Civil Engineering andArchitecture,Henan University of Technology, Zhengzhou 450001,China)

∶The basic principle of independent component analysis(ICA)is briefly introduced.The ICA and random decrement technique(RDT)are combined and used to identify modal parameters of structures under random excitation.Both numerical and experimental results show that the ICA can extract the modal coordinates and estimate the mode shape vectors from the random response signals of the structures directly.Free vibration responses can be obtained from the modal coordinates by using RDT.Finally,the natural frequencies and damping ratios are calculated by using the classical one-DOF technique.It can be seen that the proposed method is effective since it only uses the output response of the vibration system for analysis,and is suitable for modal parameter identification of the structures under random excitation.

∶vibration and wave;modal parameter identification;independent component analysis;random excitation;signal processing

O422.6< class="emphasis_bold">文献标识码：ADOI编码：

10.3969/j.issn.1006-1335.2014.06.040

1006-1355(2014)06-0178-06

2014-04-24

国家自然科学基金资助项目（51178164）；

河南工业大学高层次人才基金项目（2011BS007）；

郑州市科技计划项目（院士工作站建设计划）（项目编号：131PYSGZ205）。

静行（1982-），男，副教授，博士，主要从事结构模态分析与模态实验方面的研究。

E-mail∶hautjh@126.com