油底壳流固耦合动力学特性分析

陈冬冬，王 辉，杨景玲，李 良，宋兆哲

（1.长城汽车股份有限公司 技术中心，河北 保定071000；2.河北省汽车工程技术研究中心，河北 保定071000）

油底壳流固耦合动力学特性分析

陈冬冬1,2，王 辉1,2，杨景玲1,2，李 良1,2，宋兆哲1,2

（1.长城汽车股份有限公司 技术中心，河北 保定071000；2.河北省汽车工程技术研究中心，河北 保定071000）

阐述了油底壳、油液耦合系统模态分析建模方法，对油底壳的结构模态和耦合模态进行了计算，并通过模态试验对模态结果进行了验证。测试结果表明，无论是结构模态还是耦合模态，其测试结果与计算结果都具有很好的一致性。进一步研究发现，油液不会对油底壳模态振型产生大的影响，但会使油底壳的模态频率明显下降；油液质量是导致油底壳模态频率下降的主要原因，而油液的体积模量对油底壳模态频率影响很小。

振动与波；流固耦合；油底壳；模态试验；耦合模态

油底壳属于薄壁件，是发动机的主要发声零件之一，对发动机的声音品质具有重要影响[1—3]。因此，有必要对油底壳的动态特性进行研究。在以往的文献中，大都只考虑油底壳自身的结构模态，而未考虑油液对油底壳结构模态的影响[2，3]，或者将流体对固体的作用以固体附加质量形式进行模拟[4]。为对油底壳振动特性进行分析，并为进一步的声辐射计算提供支持，本文首先对油底壳进行了模态计算和模态测试，保证了油底壳结构模型的正确性，然后在此基础上建立了考虑油液和油底壳之间耦合效应的流固耦合模型，并通过模态试验对计算结果进行了进一步验证。试验结果表明，本文的建模方法具有很好的准确性，对油底壳耦合特性分析和进一步的声学预测具有重要意义。

1 流固耦合模态分析有限元法[5]

在流固耦合问题中，需要把结构动力方程、流体运动方程和流体连续性方程综合考虑。利用Galerkin变换，离散理想气体的声波方程，不考虑流体边界由于结构的阻尼导致的声能耗散，可以得到有限元分析的声学波动矩阵方程

考虑声压对结构振动的影响时，需要在界面上加上流体压力载荷向量，此时无阻尼结构动力学有限元方程可表述为

式中[Me]、[Ke]分别表示结构质量、刚度矩阵，{Fe}为结构激励力向量，{Ue}为节点位移分量向量。

方程(1.1)和(1.2)描述了声固完全耦合的结构流体运动方程，用统一的矩阵形式表示为

式中[Mfs]=ρ0[Re]T；[Kfs]=-[Re]。

2 无油状态下油底壳模态分析

2.1 油底壳有限元建模与结构模态计算

在Hypermesh中对冲压油底壳进行抽取中面处理，然后进行面网格划分。油底壳基本单元尺寸为4 mm，单元类型为Shell63，材料密度为7.85×103kg/ m3，弹性模量为2.1×1011Pa，油底壳的有限元的模型如图1所示。将模型以cdb文件格式导出，然后在ANSYS中完成油底壳自由模态计算。

图1 油底壳结构有限元模型

2.2 有限元模型试验验证

为验证有限元模型的合理性，采用LMS测试系统对油底壳进行了模态试验，试验时用橡皮筋将油底壳悬挂起来，试验条件如图2(a)所示。

表1列出了前5阶模态频率的测试结果和计算结果，图3中给出了前3阶模态振型的测试结果和计算结果（左侧为测试结果，右侧为计算结果）。

对比结果表明，前5阶模态振型具有很好的一致性，模态频率最大误差值在5%以内，可以说明油底壳有限元模型的正确性。

图2 测试现场

表1 无油状态下油底壳的模态频率

3 油底壳流固耦合模态分析

3.1 耦合有限元建模与耦合模态计算

在油底壳有限元模型的基础上建立包含油液的有限元耦合模型，需要注意的是，耦合面处结构网格和流体网格的节点必须重合，但不连续。油液部分采用ANSYS中的Fluid 30单元进行模拟，油液基本单元尺寸为4 mm，油液密度为8.86×102kg/m3，声速为1 487 m/s，油底壳的流固耦合有限元模型如图4所示。

将模型以cdb文件格式从hypermesh中导出，然后在ANSYS中读入。在ANSYS前处理器中利用节点耦合命令CPINTF将结构网格和流体网格在耦合面处“缝合”起来，并对耦合面施加耦合命令SF，FSI，最终完成耦合有限元模型的创建。在ANSYS求解器模块中，对液面施加0声压边界条件，选用非对称求解法对耦合模型进行自由模态求解。

3.2 耦合模型试验验证

为验证模型的合理性，对装满油状态下的油底壳进行了模态试验，试验条件如图2(b)所示。

表2给出了前5阶耦合模态频率的测试结果和计算结果，图5中给出了前3阶耦合模态振型的测试结果和计算结果（左侧为测试结果，右侧为计算结果）。

图3 油底壳前3阶模态振型

图4 油底壳流固耦合有限元模型

表2 装满油状态下油底壳的耦合模态频率

对比结果表明，前5阶耦合模态振型具有很好的一致性，模态频率最大计算误差为5.18%，可以说明油底壳耦合模型的正确性。

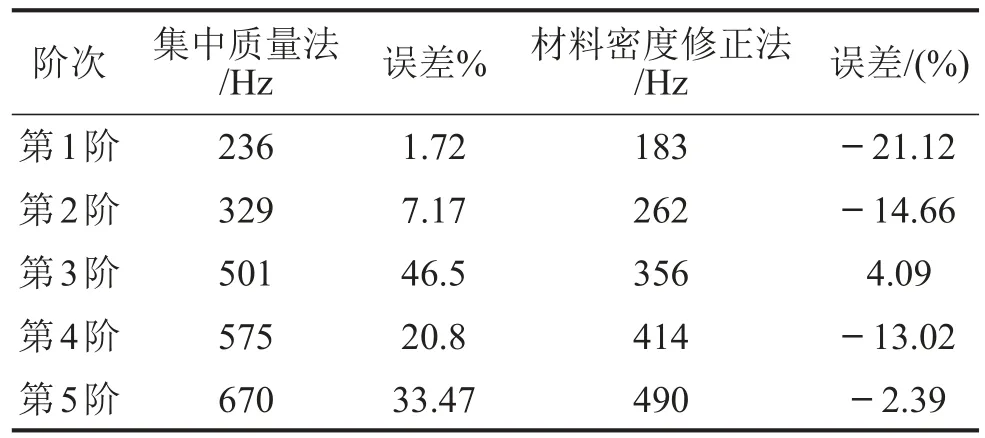
表3 不同油液建模方法下的油底壳模态频率

为验证流固耦合方法的优越性，此处对油液的其它常用建模方法进行讨论。表3给出了采用集中质量均布法（将Mass 21单元均布在油底壳内侧湿壁处的各节点上）、材料密度修正法（增加油底壳湿壁区域的材料密度）时的油底壳前5阶模态频率计算结果以及与测试结果的相对误差。两种方法的最大计算误差均超过了20%，明显大于流固耦合计算方法。由此可以说明流固耦合建模方法在求解精度上的优势。

3.3 结果分析

通过对比图3、图5中的模态振型可以发现，油液对油底壳的整体振型影响不大。

表4给出了无油状态和装满油状态下油底壳模态频率测试值。对比表中的数值可以发现，油液的存在使油底壳的模态频率明显下降，且随着模态阶次的增加下降值逐渐变大，说明油液对油底壳的高阶模态影响更为明显；前5阶模态频率的差异率最大值达到了37%，说明不能忽视油液与油底壳之间的耦合作用。

表4 无油状态和满油状态下油底壳的模态频率

在图6中，油底壳的模态频率随油液密度的减小而近似成线性升高，且增长率随模态阶数的变大而增大；在图7中，油底壳的模态频率基本上不随油液体积模量的变化而变化。以上情况可以说明，油

图5 油底壳前3阶耦合模态振型

液的质量是导致油底壳模态频率下降的主要因素，而体积模量对油底壳模态频率的影响不大。

图6 油底壳前5阶耦合模态频率随油液密度的变化曲线

图7 油底壳前5阶耦合模态随油液声速的变化曲线

4 结语

(1)试验模态证明本文中的油底壳流固耦合有限元建模方法是正确的，可以用于油底壳动力学分析；

(2)油液对油底壳整体振型影响不大，但会导致油底壳模态频率明显下降；

(3)油液对油底壳高阶模态频率影响较大，因此在对油底壳进行声辐射分析时不能忽视油液的影响；

(4)油液质量是导致油底壳模态频率降低的主要原因，而油液的体积模量对油底壳模态频率的影响不大。

[1]庞剑，谌刚，何华.汽车噪声与振动—理论与应用[M].北京：北京理工大学出版社，2006.

[2]方华，王天灵，李盛成，等.柴油机油底壳辐射声场的仿真研究[J].噪声与振动控制，2007(5)：115-118.

[3]邓晓龙，张宗杰，胡昆鹏.内燃机油底壳模态分析及噪声预测[J].噪声与振动控制，2003(2)：29-31.

[4]郭昂，于洪亮，宋玉超.油液对油底壳模态的影响分析[J].大连海事大学学报，2011，37(1)：118-123.

[5]马天飞，林逸，张建伟.轿车车室声固耦合系统的模态分析[J].机械工程学报，2005，41(7)：225-230.

[6]李增刚，詹福良.Virtual.Lab Acoustics声学仿真计算高级应用实例[M].北京：国防工业出版社，2010.

Fluid-structure Coupled Model for ModalAnalysis of an Oil Pan

CHEN Dong-dong1,2,WANGHui1,2,YANG Jing-ling1,2,LI Liang1,2,SONG Zhao-zhe1,2

(1.Technical Center,Great Wall Motor Company Limited,Baoding 071000,Hebei China; 2.HebeiAutomobile Engineering Technology and Research Center,Baoding 071000,Hebei China)

∶The structure model and fluid-structure interaction(FSI)model of an oil pan are built respectively,and the building procedure of FSI model is introduced in detail.Both models are verified by comparing modal results of simulation with those of modal testing.Their modal shapes and eigenvalues are discussed carefully.The results show that engine oil has less influence on modal shape of the oil pan,but can reduce the modal frequency of the oil pan obviously.Mass of the engine oil is the main factor to reduce the modal frequency,while bulk modulus of the engine oil has little impact on the modal frequency.

∶vibration and wave;fluid-structre interaction(FSI);oil pan;modal testing;coupled mode

TB533+.2< class="emphasis_bold">文献标识码：ADOI编码：

10.3969/j.issn.1006-1335.2014.06.004

1006-1355(2014)06-0017-03+24

2014-04-11

陈冬冬（1986-），男，河南驻马店人，硕士，目前从事车辆振动与噪声控制研究。

E-mail∶chendongdong1108@163.com