基于响应面法的臂架模态参数快速识别方法

谭金虎，阳 鹏，杨 川，曾 光

(1.湘潭大学 机械工程学院，湖南 湘潭411105；2.中联重科股份有限公司，长沙410013；3.建设机械关键技术国家重点实验室，长沙410013)

基于响应面法的臂架模态参数快速识别方法

谭金虎1，阳 鹏2,3，杨 川2,3，曾 光2,3

(1.湘潭大学 机械工程学院，湖南 湘潭411105；2.中联重科股份有限公司，长沙410013；3.建设机械关键技术国家重点实验室，长沙410013)

近几年，随着市场对机械性能的要求愈发严苛，工程机械臂架工作空间的演变呈现出更庞大更复杂的趋势，这一趋势直接导致研发过程中试验困难且耗时长。以臂架模态参数识别工作为例，不同姿态臂架的模态参数变化难以估计，工程实际中常使用有限元法来解决此类问题，但工作效率通常较低。引入响应面法，建立某消防车臂架第一阶模态固有频率的响应面模型，获取其第1阶模态固有频率，针对多姿态下消防车臂架模态参数识别工作提出一种快速有效的解决方案。结果表明，与有限元法相比，引入响应面法对100个姿态下消防车臂架模态进行预测，在保证与有限元计算结果相对误差不超过2%的前提下，其计算速度提升近10倍。

振动与波；响应面法；消防车臂架；模态参数识别；有限元法

随着经济和科技发展，大型建筑迅速涌现，市场对消防车、泵车臂架性能要求越发严苛，消防车以及泵车的臂架臂展规模屡创新高[1]，这一现状直接导致臂架工作空间复杂、试验困难且建模仿真时间骤增。

研究人员通常利用有限元及多体动力学等手段来确定臂架各姿态下的工作特性。例如，张蕊华[2]等人基于Adams对五节折叠式消防车臂架工作空间进行了分析，刘杰[3]等人选取四节臂混凝土泵车臂架的两个姿态建立了柔性多体动力学模型进行动力学研究，结果表明前者工作效率并不理想。

引入响应面法能够有效地解决此类工作空间复杂带来的时间成本骤增问题。响应面法一般用于变量优化，因其在优化设计上的优越性逐步受到了各个领域的关注。李亚东[4]等人基于响应面法建立了预测火炮扭力轴疲劳寿命响应面模型，得到了低周疲劳寿命的概率分布。张运涛[5]等人基于响应面法对大跨连续刚构桥的长期变形量进行了预测。在动力学研究范畴内，周林仁[6]等人应用响应面法建立了某大跨斜拉桥实验室物理模型设计参数与动力特性之间的响应面模型，其响应面模型对频率的拟合精度达到预期水平。实践证明，响应面法在快速预测工作范畴内有效可行。

本文针对中联某款消防车臂架模态参数识别工作进行研究，通过建立响应面模型，快速有效地对消防车臂架的1阶模态固有频率进行预测，提出了基于响应面法的消防车臂架多姿态下模态参数快速识别方法。

1 响应面法

响应面法由K.G.Wilson和G.E.P.Box共同提出，其本质是一种有效处理多变量问题的数量统计方法。为方便解释，假定变量数值为3，则响应值W与变量下x、y、z具有w=f(x，y，z)的函数关系,在三维空间内能够构造出一个真实的曲面，响应面法则是通过抽取一定量的样本拟合出一个响应曲面，当抽样方法以及其他影响因素达到了精度要求，此响应面就可以无限逼近真实曲面。响应面模型多项式阶数越高精度越高，但是相应的确定模型所需要的样本点数量也越多，所以常使用二次多项式来表示响应面函数

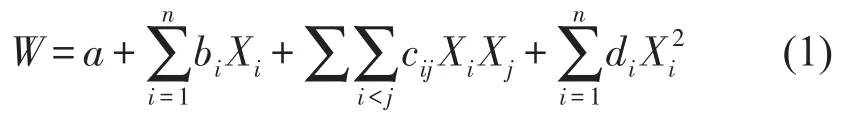
针对本文研究，只需确定变量选取方案，在变量设计空间内进行抽样得到m组变量Xm，便能使用有限元法得到相应的响应值w={w1,w2,w3,w4….wm}，将响应值及对应变量值带入式（1），使用最小二乘法便能确定ai、bi、cij、di，得到响应面近似数学模型。

为了验证上述方法的适应性，还需要对响应面模型进行精度分析。采用决定系数R2和调整的决定系数R2

adjust对响应面模型进行精度分析。R2、R2

adjust定义如下

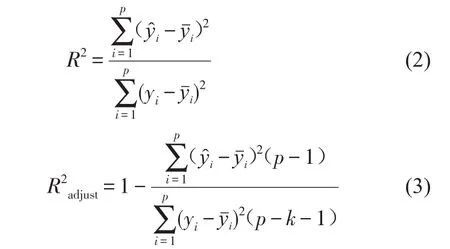
adjust值越接近1，说明响应面模型精度越高。

为避免“龙格效应”造成的试验样本点处精度较高，而非试验样本点处精度较低，应检验响应面模型在非实验样本点处的外插精度，检查其相对误差，相对误差定义如式(4)所示

图1为获得响应面模型的步骤：

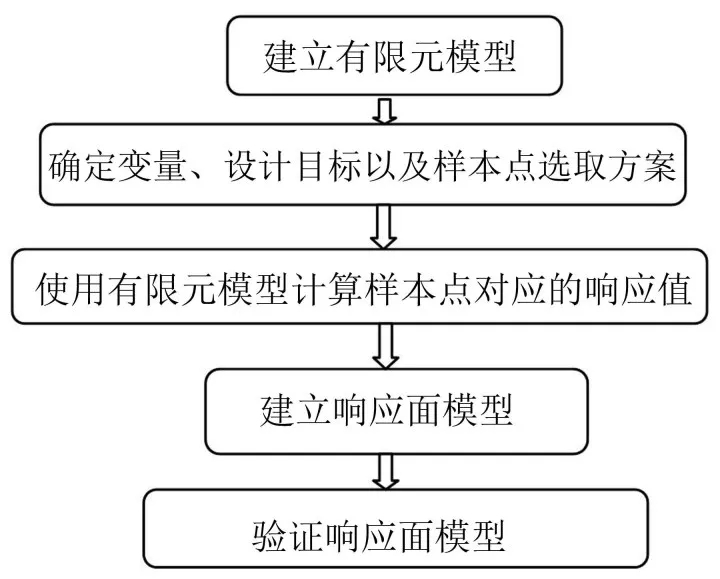
图1 建立响应面模型的流程图

2 算例分析

2.1 臂架有限元模型的建立及模态参数影响因素预分析

本文选取中联某款登高平台消防车臂架为研究对象，此款消防车主臂由六节臂组成，副臂由三节臂组成，其中2—6号臂、8—9号臂能自由伸缩。如图2所示。

消防车臂架单节臂为箱体结构且壁薄（6～10 mm），遂采用ABAQUSS 4壳单元建立有限元模型，材料选用合金钢，弹性模量为206 GPa，泊松比为0.3，密度为为确定设计目标及变量方案对消防车臂架有限元模型进行如下预分析：

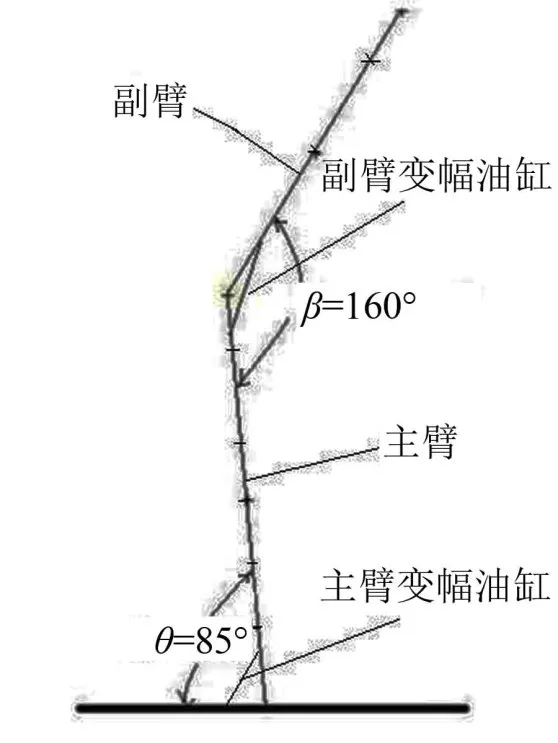
图2 臂架示意图

(1)对臂架进行四次伸缩（在角度不变的情况下七节伸缩臂同时缩短1 m记为一次伸缩）分别进行有限元计算，计算结果如图图3所示。

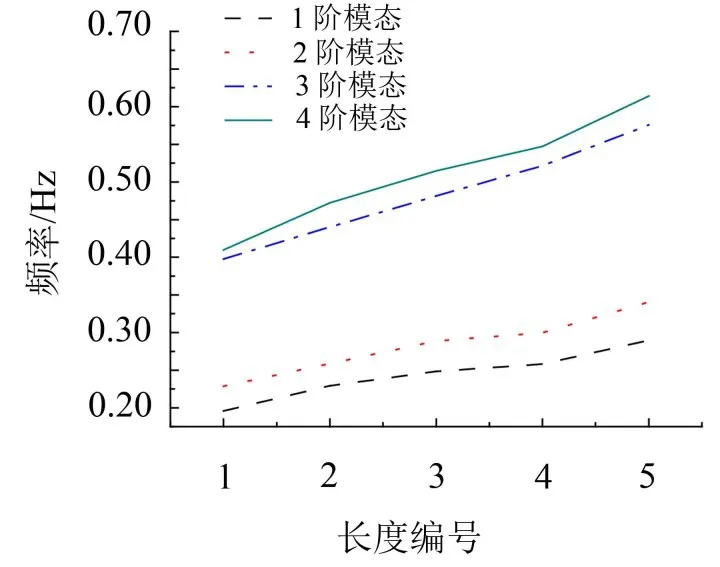
图3 长度变化对臂架模态固有频率影响

(2)主臂与地面夹角保持不变，对副臂进行姿态变换（变换一次姿态大概需要10 min）。各姿态前四阶模态固有频率计算结果如图4所示。

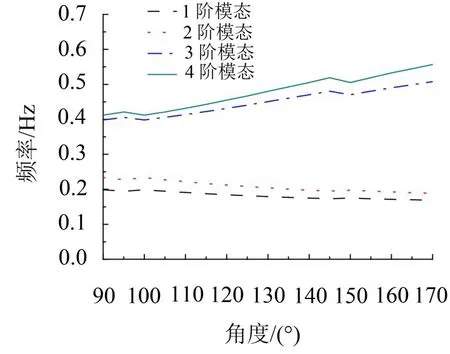
图4 臂架之间夹角大小对模态固有频率影响

数据表明各阶模态固有频率随长度缩短数值有明显的上升趋势。数据表明夹角的变化对臂架各阶模态固有频率有显著影响。

2.2 设计目标以及变量方案的选取

通常低阶模态在整体模态占主导地位。本文选取第1阶模态固有频率为设计目标。经上小节分析，臂架长度与臂架角度对臂架模态固有频率皆有影响，本文选取主臂与地面夹角θ（θ=0∘～85∘），副臂与主臂之间夹角β（β=0∘～160∘）为设计变量。

2.3 抽样方法的选定

抽样是试验设计中的一个概念，选择正确的抽样方法能够在减少工作时间的同时保持试验结果精度。拉丁超立方抽样方法是近几年被广泛使用的抽样方式，长期实践证明了拉丁超立方抽样的优越性[10]。

为确保响应面模型精度，抽样样本数应维持在响应面模型非常数项个数k的1.5—3倍。则样本选取量m定义如式(5)所示

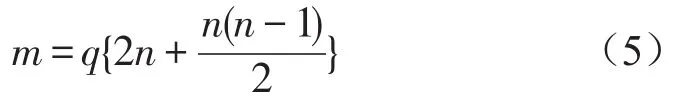
其中q=1.5～3，n为变量个数。

本文采用拉丁超立方抽样抽取十组变量。抽取的设计点如表1所示。

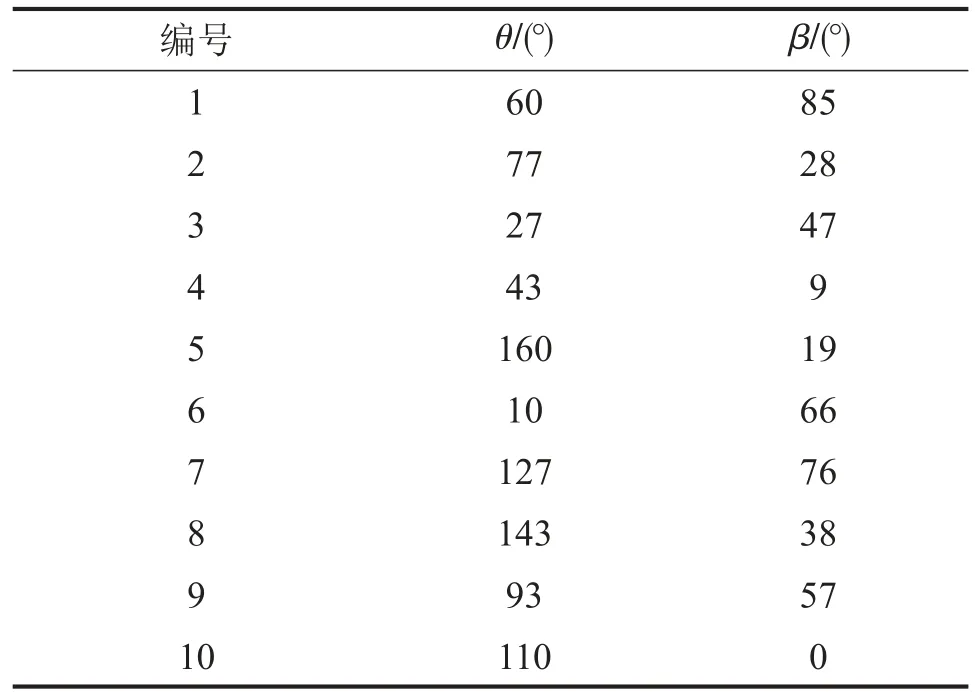
表1 拉丁超立方抽样法得到的设计点

2.4 响应面模型的确定

通过有限元模型计算表1中10组姿态变量，对应响应值如下表2所示。

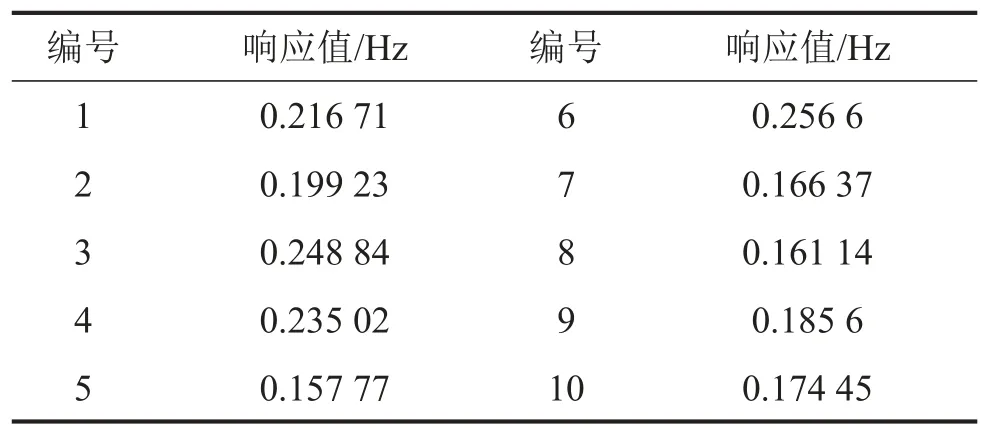
表2 有限元模型得到的响应值

将表1、表2数值带入式（1）使用最小二乘法进行求解，具体操作在Matlab中进行，Matlab编程后能迅速得到响应面模型各项系数及决定系数R2和调整的决定系数R2adjust[11，12]。如表3、表4所示。

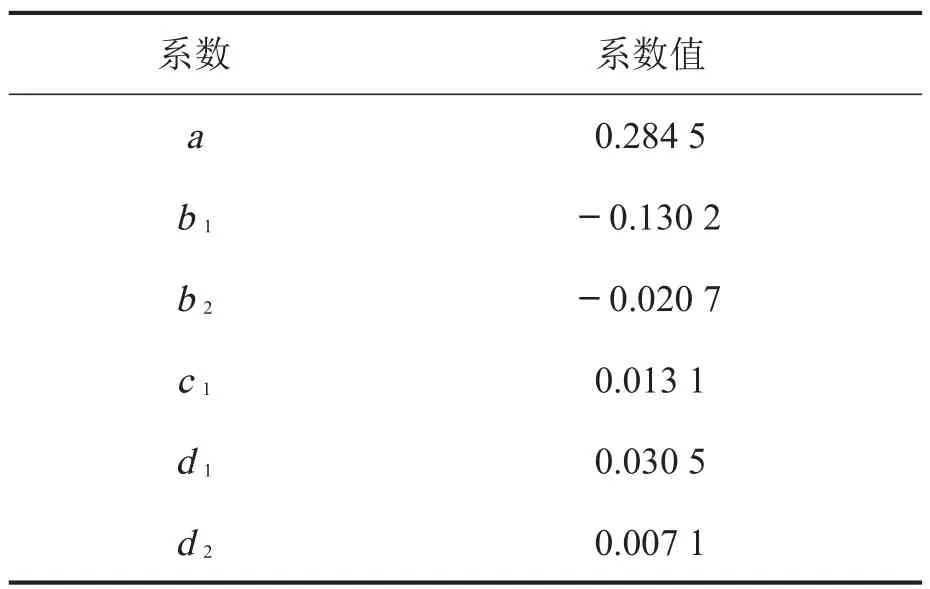
表3 响应面模型多项式各项系数

表4 决定系数及调整决定系数

2.5 响应面模型的验证

根据决定系数以及调整决定系数可以看出响应面模型精度良好，为进一步研究响应面模型的精度及快速识别模态参数的能力，重新随机抽取五组变量数据，分别使用有限元模型和响应面模型进行计算并使用式（4）对其进行相对误差分析。计算结果如下表5、图5所示。

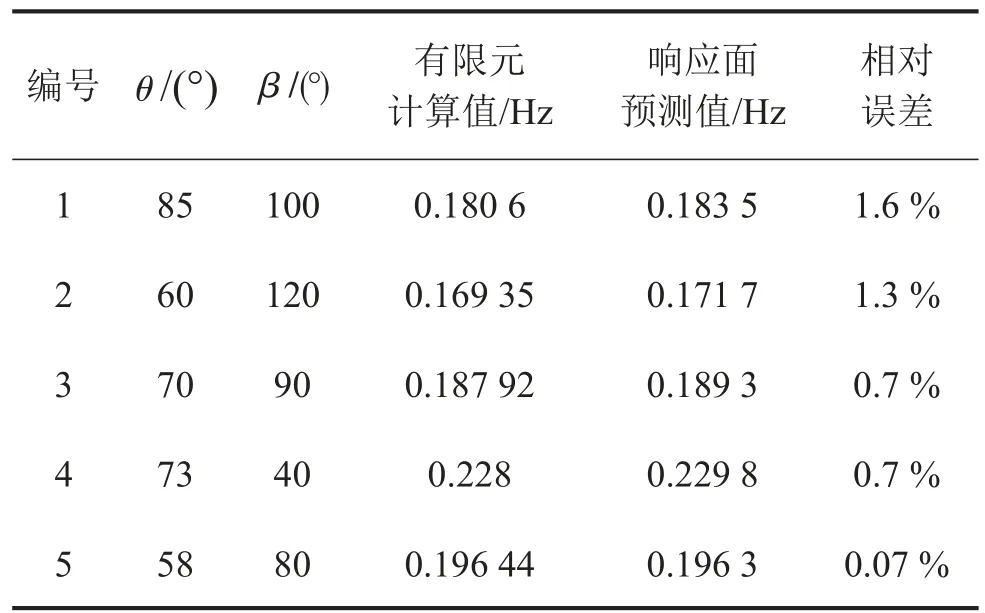
表5 有限元模型与响应面模型计算结果对比

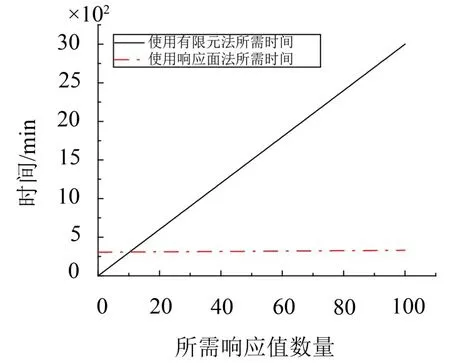
图5 有限元模型与响应面模型计算效率对比

根据以上数据得知，有限元模型计算臂架单个姿态下1阶模态固有频率需约30 min，建立响应面模型时间约为300 min（10次有限元模型姿态变化、约束施加及计算时间计算在内），响应面计算一个姿态下1阶模态固有频率只需10 s。当所需响应值数量小于11时，使用响应面模型并没有优势，随着所需响应值数量增大，假定需要100个姿态下臂架1阶模态固有频率，使用有限元模型计算需要3 000 min，而使用响应面模型计算只需要320 min，工作效率提高近10倍。因此，利用响应面法对多姿态下臂架的多阶模态参数进行识别具有显著的优越性。

3 结语

本文采用响应面法预测了消防车臂架固定长度下不同姿态的一阶模态固有频率。预测结果与有限元计算结果相比，相对误差不超过2%。随着所需响应值的增长，响应面模型的计算效率将更具优越性。因此，采用响应面法能快速的识别多姿态下的臂架模态参数，有效地解决臂架工作空间复杂带来的臂架模态参数识别工作时间成本骤增问题。

[1]江爱林，徐国荣.登高平台消防车结构设计发展研究[J].机械设计与制造，2013，22（05）：219-221.

[2]张蕊华，杨松，朱银法.基于ADAMS对一种新型消防车臂架工作空间分析[J].机械设计与研究，2013，29（01）：123-125.

[3]刘杰，戴丽.混凝土泵车臂架柔性多体动力学建模与仿真[J].机械工程学报，2007，43(11)：131-135.

[4]李亚东，郑坚.基于随机响面法的扭力轴疲劳寿命仿真预测[J].系统仿真学报，2011，23（09）：1884-1888.

[5]张运涛，孟少平.基于响应面法的大跨连续刚构桥长期变形预测[J].土木工程学报，2011，44（08）：102-106.

[6]周林仁，欧进萍.大跨桥梁参数识别响应面方法中的近似函数及样本选取[J].计算力学学报，2012，29（03）：306-313.

[7]杨川，于德介.汽车关门噪声优化方法的研究汽车工程[J].汽车工程，2013，35（03）：243-248.

[8]王彬星，郑四发.驾驶室声场响应面仿真模型的构建及应用[J].噪声与振动控制，2011，6(03)：60-64.

[9]包键，成艾国.区间响应面悬置固有频率匹配研究[J].噪声与振动控制，2011，4(02)：21-24.

[10]刘纪涛，刘飞.基于拉丁超立方抽样及响应面的结构模糊分析[J].机械强度，2011，33（01）：73-76.

[11]约翰马修斯.数值方法（第三版）[M].上海：电子工业出版社，2010.188-207.

[12]桂劲松，康海贵.结构可靠度分析的响应面法及其Matlab实现[J].计算力学学报，2004，21（06）：683-687.

Fast Identification Method of Boom Modal Parameters Based on Response Surface Method

TAN Jin-hu1,YANG Peng2,3,YANGChuan2,3,ZENGGuang2,3

(1.School of Mechanical Engineering of Xiangtan University,Xiangtan 411105,Hunan China; 2.Zoomlion Heavy Industry Science and Technology Co.Ltd.,Changsha 410013,China; 3.Skate Key Laboratory of Key Technologies on Construction Machinery,Changsha 410013,China)

∶In recent years,with the development of the market demand for mechanical properties of engineering construction machinery,it is necessary that the boom of trucks work in large space with complex movement.This necessity will lead to the difficulty and long period of design and test in R&D process of the machinery.For example,in the boom’s modal parameter identification,it is difficult to estimate the change of the modal parameters of booms in different gestures.Usually,finite element method is employed to solve such problems,but this method is less efficient.In this paper,the Response Surface Method is introduced.The response surface model of a fire truck’s boom is established and its natural frequency of the first-order modal is obtained.A fast and efficient solution scheme for modal parameter identification of the fire-truck’s boom is proposed.The research shows that compared with the finite element method,the computational efficiency of the response surface method for predicting the modal parameters of 100 gestures of the boom is increased by nearly ten times,the relative error between the two methods is less than 2%.

∶vibration and wave;response surface method;boom of fire truck;modal parameters identification;finite element method

TH113< class="emphasis_bold">文献标识码：ADOI编码：

10.3969/j.issn.1006-1335.2014.06.006

1006-1355(2014)06-0025-04

2014-02-11

国家863计划项目：工程机械共性部件再创造关键技术及规范(2013AA040203)

谭金虎（1987-），男，湖南郴州人，硕士研究生，主要研究方向：工程机械NVH性能开发。

杨 川，男，博士。

E-mail∶494684231@gg.com