基于多尺度局部保持投影的轴承故障特征增强方法

张晓涛，唐力伟，王 平，邓士杰

（军械工程学院 火炮工程系，石家庄050003）

基于多尺度局部保持投影的轴承故障特征增强方法

张晓涛，唐力伟，王 平，邓士杰

（军械工程学院 火炮工程系，石家庄050003）

针对轴承故障声发射信号的非线性特性，及易受背景噪声干扰的特点，提出一种多尺度局部保持投影方法。通过小波包分解实现一维信号的多尺度构造，利用近邻图保持信号局部流形信息，通过局部保持投影将信号变换到新的坐标空间下，实现故障特征增强。仿真和实验信号处理结果表明，多尺度局部保持投影方法在轴承故障增强检测中效果显著。

振动与波；局部保持投影；多尺度；特征增强；故障诊断

声发射（Acoustic emission,AE）对齿轮箱故障非常敏感，是一种高灵敏度故障检测方法[1]。英国Cranfield大学的David Mba采用声发射对齿轮箱故障进行状态监测研究，其研究成果表明，声发射比传统振动检测方法对齿轮箱微弱故障的检测更加灵敏[2]，国内目前相关的研究还比较少。声发射信号具有高频宽带特性，易受背景噪声干扰，有用信息往往被淹没，并且由于传递衰减畸变，故障声发射信号往往具有较强的非线性特性。

流形学习是一种非线性的机器学习算法，类比人类的流形学习规律，试图使计算机能够学习到原始数据的几何结构和内部规律[3]。2000年在science杂志同一期上的三篇文章奠定了流形学习研究的基础，流形学习认为原始数据的特征可以通过投影空间的流形结构进行表达，典型流形学习方法包括局部保持投影[4]、局部线性嵌入[5]、保距特征映射[6]等。在线性特征增强方法中，多尺度线性特征增强方法[7,8]已有应用，但线性方法在坐标转换中，仅考虑数据的全局信息，无法保持数据局部流形结构不变，对数据非线性的处理能力不足，文中类比线性处理方法，结合小波包分解与局部保持投影，提出一种多尺度局部保持投影算法，并采用仿真和实验信号对其故障增强性能进行验证。

1 多尺度局部保持投影的理论基础

1.1 局部保持投影方法

局部保持投影（Locality Preserving Projection，LPP）是一种典型的流形学习方法，其处理过程能够有效的保持数据局部流形结构不变，并实现原始样本在投影空间中差异化的增强表达。LPP是一个投影优化过程，假设存在数据x=[x1,x2,…,xn]其投影变换的目标函数如下：

式中xi和xj为原始数据x的样本，W为投影矩阵，sij为权重系数，如式2所示，由k近邻法构造近邻图计算，表征数据样本之间相似度，所有权重系数构成权重相似矩阵S，对角矩阵其中近邻参数k根据具体情况进行设置。

其中β为所有样本之间欧式距离均值的平方。

对LPP的目标函数进行运算可得下式

式中L=D-S，称为拉普拉斯矩阵，S为权重矩阵，由权重系数sij组成，对角矩阵D含义与前面相同。

LPP最佳投影矩阵W基于拉格朗日乘子法计算，通过求解式4的广义特征向量得到投影矩阵W。

1.2 多尺度局部保持投影

多尺度局部保持投影(multi-scale locality preserving projection,MSLPP)是一种结合小波包分解与局部保持投影的信号处理方法。文献[9]认为工业数据是多尺度变化的，当出现故障特征，原始数据在各个尺度内的信号特征会发生不同变化。因此MSLPP方法首先对原始数据进行小波包分解，然后在各个尺度内对重构信号进行最优方向投影，保持信号局部流形结构信息。MSLPP的处理流程如图1所示，首先对原始数据y进行n层小波包分解，在各个子频带内重构得到2n个多尺度分量Cn0,…,Cni,…,Cnk，其中k=2n-1，i=0,…,k。采用多尺度局部保持投影方法将重构分量映射到新的投影坐标下，得到重构后得到特征增强信号y*。

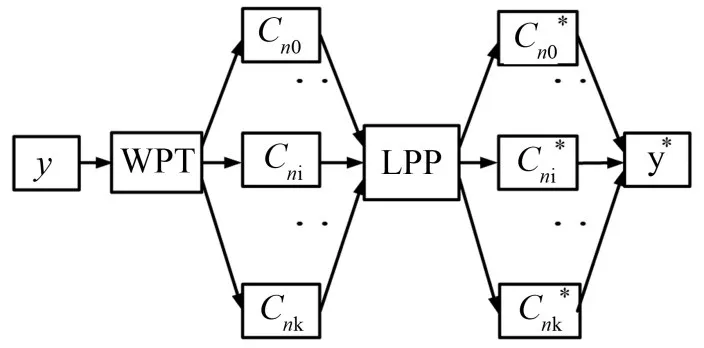
图1 MSLPP流程图

MSLPP在原信号各子频带内实现保持分量的局部流形信息，并在新的投影坐标下抑制多尺度分量间的信息冗余，重构信号y*的幅值经投影后，不再具有原始幅值的物理意义，但信号的频率成分依然反映故障的特征信息，因此通过求解重构信号的包络谱即可实现故障诊断。

2 仿真信号分析

采用仿真信号对MSLPP的性能进行分析，仿真信号y(t)设置如下：冲击共振频率10 kHz，干扰轴频分别为100 Hz和200 Hz正弦信号，幅值分别为2.1和1.8，采样频率fs=30 kHz，数据长度n=10 240点。设置均布10个故障，故障频率约fr=29.2 Hz，其计算如式5所示。仿真信号如式6所示。

在仿真信号y(t)中添加高斯白噪声n(t)后得到含噪声的仿真信号yn(t)=y(t)+n(t)，yn(t)的时域波形及其包络谱如图2所示。

图2 仿真信号及其包络谱

从图2中可知，信号时域波形中故障信号完全淹没在干扰轴频和白噪声中，信号包络谱中仅有100 Hz的轴频干扰成分及其倍频成分，在故障频率29.2 Hz处没有可识别的谱线，因此，从含噪声的时域信号中无法识别故障特征。

采用MSLPP方法对含噪声仿真信号进行处理，选用db 4小波，分解层数为3层，近邻参数k经过多次试验后设置为42，具有较好的计算效果。MSLPP处理后的信号时域波形及其包络谱如图3所示。

图3 MSLPP方法处理结果

从图3中可以看出，经过MSLPP方法增强处理后，时域信号的冲击特性明显，并且其包络谱在29.3 Hz（≈29.2 Hz）及其倍频处有明显的谱线，可以清楚的识别故障频率。

仿真信号的MSLPP处理结果表明，在强干扰情况下，故障冲击信号完全淹没在干扰轴频及噪声下时，MSLPP方法能够寻找最优投影方向，在新的投影坐标下保持故障局部流形信息从而增强故障特征，清楚的识别故障频率谱线，具有明显的故障特征增强能力。

3 实验信号分析

齿轮箱轴承故障产生的声发射信号幅值往往较小，容易淹没在齿轮箱运转背景噪声中，因此原始采样信号一般无法直接识别故障频率，需要进行增强处理，使特征变得易于识别。文中采用轴承内圈故障声发射信号对MSLPP方法的性能进行检验，算法参数设置与仿真分析相同。

实验齿轮箱结构原理如图4所示，故障轴承安装在齿轮箱中间传动轴上，型号6206，预置故障为线切割裂纹，宽0.05 mm，深1 mm。声发射传感器为声华R15型，全波形采集仪采样频率1 MHz。实验过程中齿轮箱空载运转，轴承内圈转速305.1 r/min，结合国标中轴承参数及内圈故障计算方法[10,11]可知轴承内圈的故障频率为27.61 Hz。

轴承故障声发射信号受传播路径的衰减、畸变以及齿轮箱各部件运转噪声的影响，原始信号时域波形干扰严重，非线性特性明显，直接求包络谱发现谱图中干扰谱线非常多，各个谱线分布没有明显规律，故障谱线不可识别，原始信号及其包络谱如图5所示。

图4 齿轮箱结构原理

图5 原始信号及其包络谱

采用MSLPP方法对原始信号进行处理，选择db 4小波，对原始信号进行3层分解，经多尺度局部保持投影变换后的信号及其包络谱如图6所示。

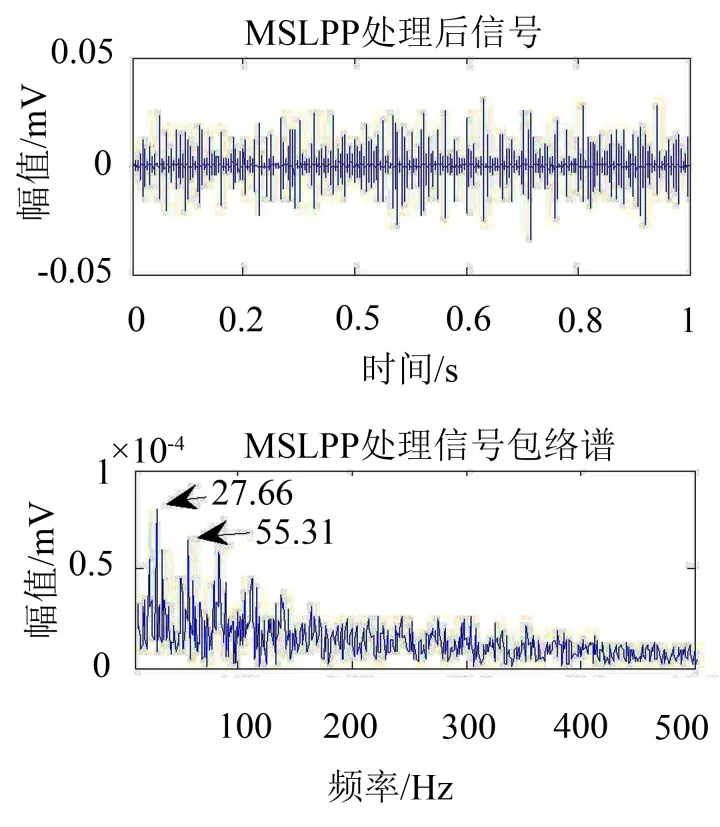
图6 MSLPP处理信号及包络谱

由于投影变换求解中对投影矩阵解算条件的限制，处理后的信号幅值不再具有明确的物理意义，但信号频率成分依然反映故障特征信息，从其包络谱中可以看到，故障频率处谱线及倍频成分衰减均非常明显，其他干扰谱线相对较小，故障频率识别容易。

4 结语

针对齿轮箱轴承故障声发射信号的非线性特性，提出一种多尺度局部保持投影方法MSLPP，通过小波包分解构造多尺度信号，从而实现一维故障信号的局部保持投影，MSLPP具有保持原始数据局部非线性流形信息的能力，是一种基于数据非线性特性的增强处理方法，仿真信号和实验信号处理结果表明，MSLPP能够有效增强故障特征，经过处理的信号包络谱中故障谱线清晰明显。

[1]Dong Sik Gu,Jae Gu Kim,Young Su An,et al.Detection of faults in gearboxes using acoustic emission signal[J].Journal of Mechanical Science and Technology,2011, 25(5)∶1279-1286.

[2]D.Mba,Raj B.K.N.Rao.Development of acoustic emissiontechnologyforconditionmonitoringand diagnosisofrotatingmachines;bearings,pumps, gearboxes,engines and rotating structures[J].The Shock and Vibration Digest,2006,38(1)∶3-16.

[3]宋涛，汤宝平，李锋.基于流形学习和K-最近邻分类器的旋转机械故障诊断方法[J].振动与冲击，2013，32(5)：149-151.

[4]李锋，汤宝平，宋涛，等.归一Laplacian矩阵有监督最优局部保持映射故障辨识[J].机械工程学报，2013，49(13)：100-105.

[5]马瑞，王家，宋亦旭.基于局部线性嵌入(LLE)非线性降维的流形学习[J].清华大学学报，2008，48(4)：582-585.

[6]孙斌，薛广鑫.基于等距特征映射和支持矢量机的转子故障诊断方法[J].机械工程学报，2012，48(9)，129-133.

[7]李宏坤，赵长生，周帅，等.基于小波包-坐标变换的滚动轴承故障特征增强方法[J].机械工程学报，2011，47(19)：74-79.

[8]尹刚，张英堂，李志宁，等.基于MSPCA的缸盖振动信号特征增强方法研究[J].振动与冲击，2013，32(6)：143-147.

[9]Manish M,Henry,Joe Q S,et al.Multivariate process monitoring and fault diagnosis by multi-scale PCA[J].Computers and Chemical Engineering,2002,26(9)∶1281-1293.

[10]夏均忠，苏涛，马宗坡，等.基于EMD的滚动轴承故障特征提取方法[J].噪声与振动控制，2013，2：124.

[11]佟雨燕，陆森林.信号相关性和EEMD-Hilbert包络在滚动轴承故障诊断中的应用[J].噪声与振动控制，2013，5：144-149.

Bearing Fault Feature Enhancement Method Based on Multi-scale Locality Preserving Projection

ZHANG Xiao-tao,TANG Li-wei,WANG Ping,DENG Shi-jie

(Department ofArtillery Engineering,Ordnance Engineering College,Shijiazhuang 050003,China)

∶Aiming at the nonlinearity and the disturbance of noise-background for acoustic emission of bearing fault,the method of multi-scale locality preserving projection is presented.The original signal is transformed into one-dimensional signal with multi-scale structure through wavelet packet decomposition,and the local manifold information of the signal is maintained by the neighborhood graph.Then,the multi-scale signal structure is converted to a new coordinate space by locality preserving projection,and the fault information can be enhanced.The results of simulation and testing data show that the multi-scale locality preserving projection has an obvious enhancement effect in bearing fault detection.

∶vibration and wave;locality preserving projection;multi-scale;feature enhancement;fault diagnosis

TH133.1

10.3969/j.issn.1006-1335.2014.06.037

1006-1355(2014)06-0166-03+173

2014-04-09

国家自然科学基金(507752169)；

军队科研资助项目([2011]107)

张晓涛（1987-），男，陕西富平人，博士生，主要研究方向为：机械性能检测与故障诊断。

唐力伟（1961-），男，博士生导师，

E-mail∶tom5157@163.com