基于改进换相面积的直流输电换相失败判别方法

刘济豪，郭春义，刘文静，许韦华，阳岳希，赵成勇，李 丹

(1.华北电力大学 电气与电子工程学院，北京102206;2.国网智能电网研究院，北京102200)

0 引 言

逆变器的换相失败是传统直流输电常见故障，其根本原因是传统直流输电的换流器件——晶闸管固有的半控特性。引起换相失败的原因有很多，如逆变侧母线电压降低、直流电流增大、触发脉冲丢失等［1］。

近年来，越来越多的传统直流输电系统投入我国交直流混合的电网［2～3］，由于交流系统故障等原因导致换相失败事故，尤其是连续换相失败事故的频繁发生，引起系统受扰产生大幅度的功率波动，对电网造成了严重冲击，甚至造成大范围停电事故［4］。而连续换相失败所造成的负面效果远远超过单次换相失败所造成的的影响，因此对连续换相失败的监测和预防具有重要工程意义。

为预防连续的换相失败，首先要判断单次换相失败的发生，当判断出单次换相失败的发生后，迅速采取预防措施，从而预防后续换相失败。因此如何准确迅速判断出单次换相失败的发生是连续换相失败预防的重要研究对象。

判断换相失败有多种方法，如关断角、临界电压跌落、换相电压时间面积等。关断角γ 是正向阻断恢复时间的电角度表示形式，利用关断角可以直接判断换相失败的发生［5］。文献［6 ～8］中介绍了关断角的计算方法，但直流工程中晶闸管数量太多导致晶闸管的关断角不易测量［9］，因此实际工程中不便以此作为换相失败的判据。文献［10］提出了临界电压跌落的概念，该方法优点是只需要判断换流母线电压与临界电压跌落的关系即可判断换相失败，容易实现，缺点在于忽略了控制系统的响应特性。文献［11 ～12］采用逆变侧交流电压的αβ 分量的幅值和零序分量来分别判断对称、不对称故障引起的换相失败。文献［13］介绍了换相电压时间面积这一概念并将其用于换相失败的理论分析，该方法作出了直流电流保持不变的假设，用换相面积作为换相失败的判据。该方法考虑了控制系统对换相电压的调节作用，但是发生换相失败时通常直流电流会急剧增大，因此该方法与实际工况有很大偏差，判断结果准确度不高。

本文将换相电压时间面积这一判据从理论上加以改进，取消了直流电流保持不变这一假设，得到改进换相面积判据。在PSCAD/EMTDC 下搭建了±800 kV 传统直流输电仿真系统，在其中分别加入交流侧单相接地故障、两相短路故障、两相接地故障、三相短路故障，并采用改进前后的换相面积判据判断换相失败。引入了故障容量这一概念，利用其对比了改进前后换相面积判据的精确度。最后，对故障时刻与换相失败的关系进行了分析。

1 换相电压时间面积判据及改进

1.1 换相电压时间面积判据

以LCC-HVDC(Line-commutated-converter high voltage direct current，LCC-HUDC)逆变器中阀1和阀3 换相过程为例说明晶闸管的换相过程［14］。阀1 向阀3 换流时，阀4，5，6 关断，无电流流过;阀2 导通，流过直流电流。换流变压器可以用三相对称的换流电感表示。将逆变器的结构简化可得到阀1 向阀3 换相时的等值电路，如图1 所示，其中Lr为换流电感，i1，i2，i3分别为换流阀1，2，3 的阀电流，Id为直流电流，ua，ub，uc为换流母线相电压瞬时值。

图1 两相换相的等值电路Fig.1 Equivalent circuit of commutation

设t1为换相开始时刻，t2为换相结束时刻，那么在t∈［t1，t2］时，由换流电感上的电压关系，得式(1):

式中:uba=ub-ua，即AB 两相之间线电压。

假设直流系统的直流电流Id保持不变，则由式(1)可得:

在t∈［t1，t2］内，同时对式(2)等号两边进行积分，得:

由于换流阀处于关断状态时，其电流为0，而在换相过程完成后，阀电流即为直流电流Id，将这两个时刻阀电流的值代入式(3)，可得:

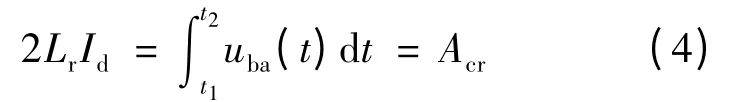
式(4)说明完成换相过程所需的换相面积为一固定值，且换相面积与直流电流成正比关系。定义该换相面积为临界换相面积Acr，其大小决定了换相过程的快慢，也决定了换相角μ的大小。

1.2 换相面积判据的改进

换相电压时间面积判据的推导过程中，假设了直流电流保持不变。然而LCC-HVDC 系统如果发生短路故障或负荷增大等容易导致换相失败的情况时，直流电流会大幅上升，这与原假设条件不相符，所以直接应用该判据来判断换相失败会导致判断精确度下降。综上所述，有必要进行理论改进以考虑直流电流的变化。

式(1)中未使用到直流电流不变的假设条件，因此可从式(1)开始进行改进换相电压时间面积法的推导。当直流电流随时间变化时，dId/dt≠0。由式(1)化简得:

在t∈［t1，t2］内，同时对式(5)等号两边进行积分，得:

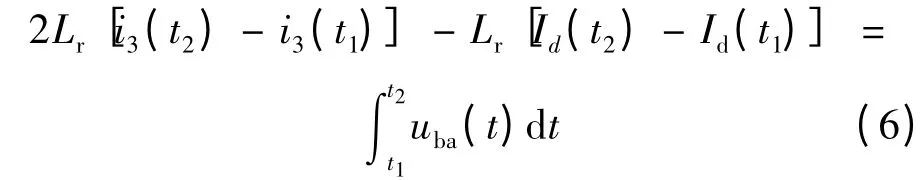
换流开始时，阀3 处于关断状态，阀3 的电流为0;换流结束时，阀3 电流上升至此时的直流电流Id(t2)，将这两个时刻阀电流的值代入式(6)，得:

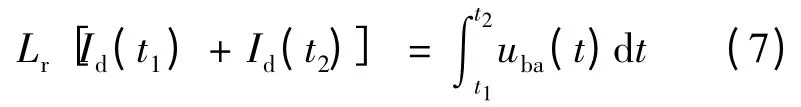
由式可以得到改进临界换相面积理论中，为了完成换相所需的换相面积，即临界换相面积为

至此，已推导得出改进换相面积判据中临界换相面积Acr的计算方法。而换流电压最大能提供的换相面积为Af为换流电压对时间的积分，其上下限分别为t1为换相开始时刻，t3为距离线电压过零点电角度为最小关断角γ0的时刻，即换流阀的最晚关断时刻。表达式如式(9)所示:

因此，判断换相失败的判据为

由改进前后的判据和Acr，Af的计算方法可以看出，直流电流波动对换相失败发生的影响体现在换相过程开始时刻和结束时刻直流电流的大小，换相过程中和换相过程以外直流电流的数值对本次换相失败并无影响。

临界换相面积与直流电流成正比关系，如果按改进前计算方法判断换相失败，不考虑直流电流的波动，当直流电流波动较大时显然判断结果与实际情况有较大偏差;将直流电流恒定这一假设取消，可以从理论上避免了直流电流波动所带来的误差。

2 基于改进换相面积的判断程序

根据改进换相面积判据，在PSCAD 环境搭建如图2 所示的换相失败判断程序。

完成换相面积的测量和换相失败的判断需要监测如下几个电气量:a.直流电流;b.阀电流;c.换相电压瞬时值(即换流母线的线电压)。

换相失败的判断程序包括以下几个步骤。

2.1 判断积分开始时刻

积分开始时刻应为换相开始时刻，此时换流阀开始关断，阀电流会迅速下降，阀电流的导数远小于0，因此可以采用阀电流的导数作为判断依据。

阀导通时，阀电流等于直流电流。故障期间，直流电流的波动，可能导致阀电流导数在阀导通期间短期为负。如果严格以阀电流是否为负作为判断标准，有可能由于直流电流的波动导致误判断。因此，将阀电流导数与直流电流导数进行比较，可以避免上述原因导致的误判断。

换相失败判断程序中采用的方法如下:采集阀电流和直流电流的瞬时值，并对这两个变量进行求导，当阀电流导数小于直流电流时为积分开始时刻，此时开始进行积分。

2.2 判断积分结束时刻

积分结束时刻应为不导致换相失败的最晚换相结束时刻，为了不导致换相失败，此时距换相电压过零点电角度为γ0。

图2 中所示方法为最小关断角为0 时的判断方法，此时将换相电压与0 相比较，判断换相电压为负的时刻，该时刻就是积分结束时刻。

如果最小关断角不为0°，则需要在线电压比较环节处将原比较量0 修改为ULinesinγ0(ULine为线电压幅值)，使积分结束时刻在与线电压过零点相距γ0的时刻。

2.3 计算换相电压能提供的最大换相面积Af。

在积分区间内对换相电压进行积分，得到换相电压能提供的最大换相面积Af。

2.4 计算临界换相面积Acr。

通过式(4)、式(8)计算得到改进前与改进后的临界换相面积Acr。

2.5 得到判断结果

将(4)、(5)中得到的Af和Acr结果做比较，得到换相失败的判断结果。

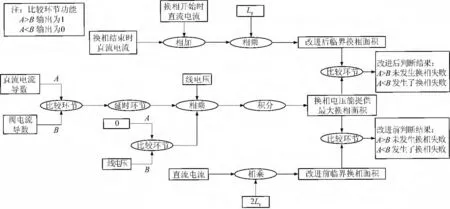
图2 换相失败判断程序Fig.2 Commutation failure judging program

3 仿真系统参数及仿真分析

3.1 仿真系统参数

本程序的仿真基于±800 kV 直流输电仿真平台，结构如图3 所示，整流侧和逆变侧的换流器各采用两个12 脉动换流器，系统其他主要设备有换流变压器、平波电抗器、滤波器、直流线路等。

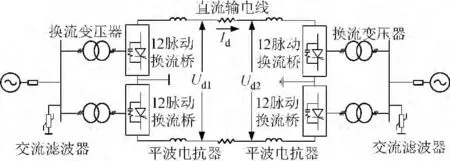
图3 ±800 kV 直流输电仿真系统结构示意图Fig.3 Structure of ±800 kV HVDC simulation system

整流侧额定运行情况下采用定电流控制，另外配置了最小触发角控制和低压限流控制，逆变侧额定运行情况下采用定关断角控制，定电流控制、电流偏差控制、低压限流控制，详细的控制保护策略见文献［14，15］。

3.2 仿真结果

为验证故障情况下，换相失败判断程序的准确性，在逆变侧交流母线处设置不同时刻发生的不同严重程度的各类故障，通过仿真得到这些情况下应用改进前、改进后两种判据的换相失败程序判断的结果和实际换相失败的情况，即可得到换相失败程序判断是否正确，综合不同故障时刻、不同故障严重程度下的判断结果得出换相失败判断程序的准确性，同时验证改进临界换相面积的理论正确性。

为了描述交流系统故障的严重程度并将其与直流功率相联系，这里引入故障容量(Fault Level，FL)［16，17］的概念，如式(10)所示，其值越大，说明故障越严重。

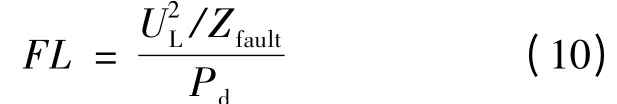
式中:UL是换流母线线电压;Zfault是故障的接地阻抗;Pd为直流系统传输容量。称导致换相失败发生的最小故障容量为临界故障容量，通过比较利用改进前后换相面积判据判断得到的临界故障容量与实际直流输电系统的临界故障容量。

图4 ～7 分别为三相短路故障、BC 两相接地故障、BC 两相相间短路故障、A 相单相接地故障的仿真结果。图中3 条曲线分别为直流输电系统的实际临界故障容量曲线、改进后换相面积判据测得的临界故障容量曲线、改进前换相面积判据测得的临界故障容量曲线。接地阻抗设为阻性，图中纵坐标为故障容量，横坐标为故障时间。

图8，9 分别为发生单相接地故障、三相短路故障时系统主要参数的仿真波形，包括交直流电压、直流功率、换相面积、阀电流、关断角。图8 对应的故障为2.006 s 发生的、故障容量80 %的三相短路故障;图9 对应的故障为2.006 s 发生的、故障容量40 %的A 相单相接地故障。

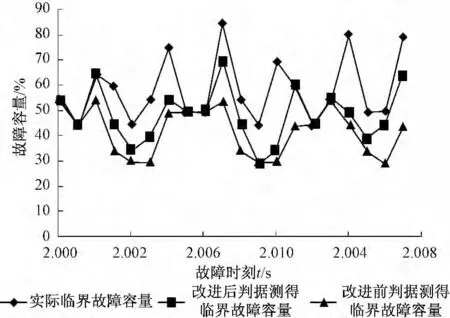
图4 三相短路故障的仿真结果Fig.4 Simulation result of three-phase short circuit fault

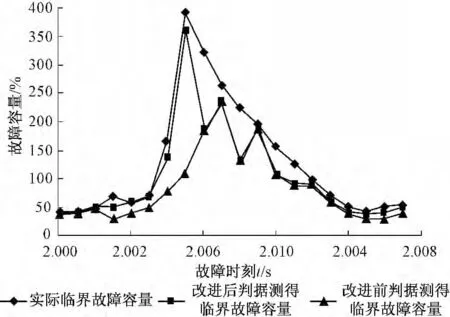
图5 两相接地故障仿真结果Fig.5 Simulation result of two-phase-to-ground fault

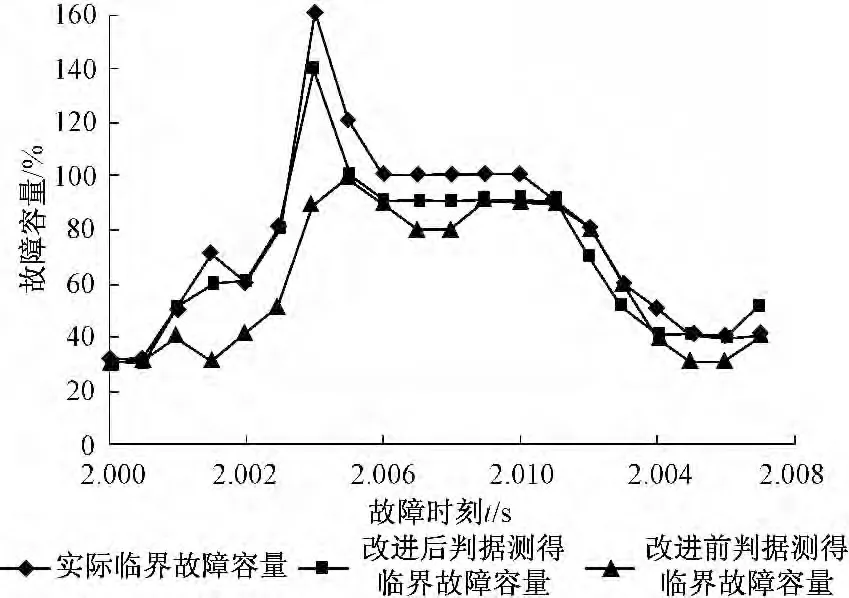
图6 两相相间短路故障仿真结果Fig.6 Simulation result of two-phase fault

3.3 仿真结果分析

(1)换相失败判断结果分析

由图4 ～7 可以得出以下结论:换相失败判断程序得到的判断结果比较准确。换相失败判断程序得到的判断结果是一个保守的结果，即存在不发生换相失败而判断为发生换相失败的情况，但不存在发生换相失败而判断为不发生换相失败的情况。

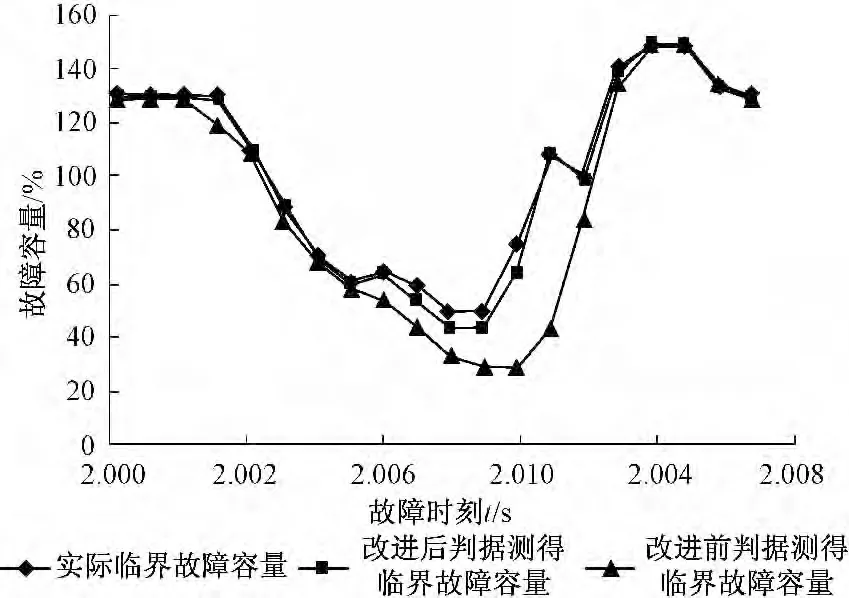
图7 单相接地故障仿真结果Fig.7 Simulation result of phase-to-ground fault

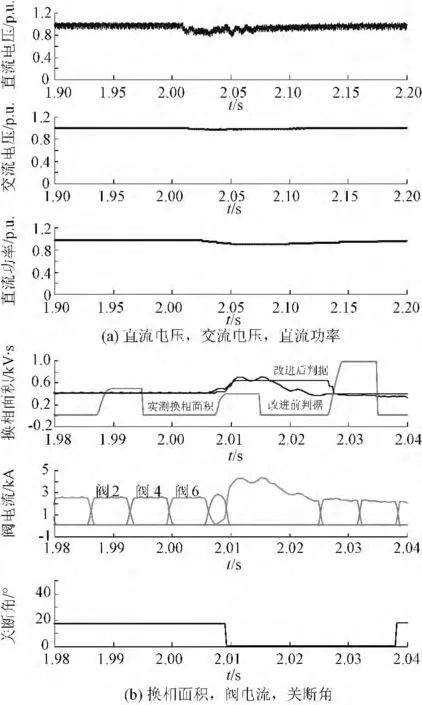
图8 2.006 s 发生故障容量80 %的三相短路故障时的仿真波形Fig.8 Simulation waveform during a three-phase short circuit fault occurred at 2.006s ( fault level: 80 %)

改进后换相面积判据判断得到的临界故障容量结果与直流输电系统的实际情况更为接近，这种现象在单相接地故障中更为明显，因此改进后换相面积判据的判断结果比改进前更准确，这也进一步验证了理论推导的正确性。

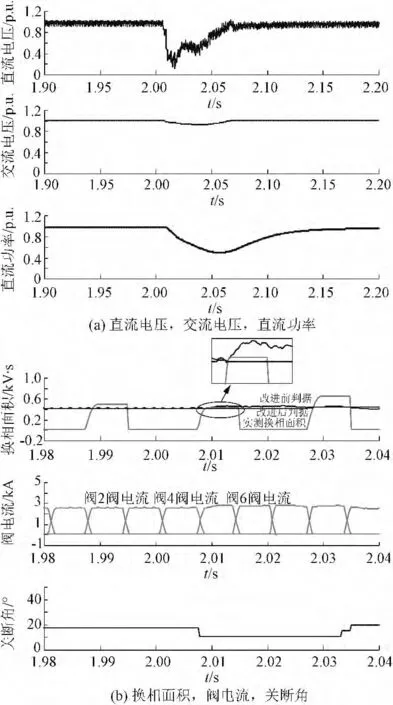
图9 2.006 s 发生故障容量40 %的A 相单相接地故障时的仿真波形Fig.9 Simulation waveform during A phase-to-ground fault occurred at 2.006s ( fault level: 40 %)

换相失败判断程序判断不准确的原因分析如下:a.从稳态时的结果来看，换相面积测量存在一定误差;b.测量换相面积时需要判断换相开始时刻，这里以阀电流导数是否为负作为判断标准，存在微小的延迟。以上两个原因都会使换相面积Af减小，从而导致判断趋于保守。

图8 中，2.006 s 发生故障容量80 %的三相接地故障时，关断角降低至0°且阀4 电流连续导通一个周期，因此本次故障导致阀4 发生换相失败。根据换相面积理论，换相失败判断程序的结果通过比较实测换相面积与判据得到，图8(a)中换相面积波形显示，改进前后Acr＞Af，因此得出的判断结果均为发生换相失败，也就是说本次故障中两种判据的判断结果都是正确的。

图9 中，2.006s 发生故障容量40 %的A 相单相接地故障时，关断角最小时为10°且阀电流波形显示各阀导通顺序正常，因此本次故障并未导致换相失败。图9(a)中换相面积波形显示:改进前的判据由于正比于直流电流，而直流电流在故障期间迅速上升，导致，Acr＞Af，因此判断结果为发生换相失败，判断错误;改进后判据只与换相过程开始和结束时刻的直流电流值有关，因此直流电流在换相结束后的波动对其无影响，得到的判断结果为Acr＜Af，即不发生换相失败，判断正确。

(2)故障时刻对换相失败影响分析

临界故障容量可以用于描述不同时刻换相失败的难易程度，临界故障容量较小时容易发生换相失败，临界故障容量较大时不容易发生换相失败。

对于同一个直流输电系统，在一个周期内不同时刻临界故障容量也不同，这里以单相接地故障和三相短路故障为例进行分析。

单相接地故障对每个6 脉动桥中的两个阀影响较大。以A 相单相接地为例，与B，C 相电压相比A 相电压下降较大，这使得在同种程度的故障下，Ucb下降幅度要小于Uab的下降幅度，以临界换相面积理论来看，换相电压下降会使交流系统提供的最大换相面积减小，也就是说A 相单相故障时，换相电压为Uab的阀4 比换相电压为Ucb的阀3容易发生换相失败;而阀4 与阀5 相比，Ua和Ub在阀4 换相时均为正，Uab=Ua－Ub，Ua降低会使Uab减小，对换相不利;Ua和Uc在阀5 换相时均为负，Uac=Ua－Uc，Ua的幅值降低，会反而使Ua的瞬时值增大，从而导致Uac增大，这对换相反而是有利的，因此，A 相单相故障时阀4 远比阀5 容易发生换相失败。由上述分析可得，A 相单相接地时，阀1 和阀4 容易发生换相失败，阀3 和阀6 次之，阀2和阀5 最不容易发生换相失败。在故障时间－故障容量平面上有两个波峰，该故障时间对应了阀1和阀4 的换相过程的时间，在上述分析与仿真结果是相符的。

三相短路故障对三相电压的影响是相同的，因此对12 脉动换流器中每个阀换相过程的影响基本相同，所以在故障时间-故障容量平面上有12 个波峰，在前一个阀换相结束而后一个阀尚未换相结束的这段时间中的不同时刻发生故障，对换相过程的影响略有差别，这也是导致换相失败的临界故障容量在不同时刻略有差别的主要原因。

4 结 论

(1)本文对临界换相面积的推导过程加以理论改进，在计算过程中考虑到直流电流在发生故障等情况时的波动，使得到的结果更贴近工程实际。在仿真结果中，对比使用改进前后换相电压时间面积判据的判断结果，改进后的判断精度较好，进一步验证理论推导的正确性，具有一定理论指导意义。

(2)本文基于改进的临界换相面积理论研究了换相失败的判断程序，用以判断系统是否发生换相失败以及发生换相失败的阀，从而为防止后续换相失败提供信息。针对不同故障类型，进行仿真，仿真结果表明判断程序是有效的。

(3)利用临界故障容量这一概念分析一个周期内不同故障时刻与故障难易程度的关系。根据仿真结果，分析了单相接地故障与三相短路故障临界故障容量随故障时间变化的规律和原因。

［1］徐政.交直流电力系统动态行为分析［M］.北京:机械工业出版社，2004.

［2］刘观起，石新聪.STATCOM 影响直流输电动态响应性能的仿真研究［J］.华北电力大学学报，2010，37 (2):20 －23.

［3］蔡泽祥，朱浩骏，白雪峰.多馈入直流输电系统的动态特性及稳定控制与分析［J］.华北电力大学学报，2004，31 (5):1 －8.

［4］何朝荣，李兴源.影响多馈入高压直流换相失败的耦合导纳研究［J］.中国电机工程学报，2008，28(7):51 －57.

［5］王渝红.交直流混合运行系统中的换相失败研究［D］.重庆:西南交通大学，2008.

［6］马玉龙，肖湘宁，江旭.交流系统接地故障对HVDC的影响分析［J］.中国电机工程学报，2006，26(11):144 －149.

［7］Wang Jing，Zhao Chengyong，Hu Jing，et al.The analysis and simulation of commutation failure and protection strategies ［C］.Weihai:4th International Conference on Electric Utility Deregulation and Restructuring and Power Techologies (DRPT2011)，2011.504 －508.

［8］吴萍，林伟芳，孙华东，等.多馈入直流输电系统换相失败机制及特性［J］.电网技术，2012，36 (5):269 －275.

［9］赵婉君.高压直流输电工程技术［M］.北京:中国电力出版社，2004.124 －126.

［10］Thio C V，Davies J B，Kent K L.Commutation failures in HVDC transmission systems ［J］.IEEE Trans on Power Delivery，1996，11 (2):946 －957.

［11］Zhang L，Dofnas L.A novel method to mitigate commutation failure in HVDC systems ［C］.2002 Power System Technology，International Conference on，2002.51－56.

［12］陈树勇，李新年，余军，等.基于正余弦分量检测的高压直流换相失败预防方法［J］.中国电机工程学报，2005，25 (14):1 －6.

［13］Chen Shuyong，Li Xinnian，Yu jun，et al.A method based on the sin-cos components detection mitigates commutation failure in HVDC ［J］.Proceedings of the CSEE，2005，25 (14):1 －6.

［14］王晶.高压直流输电典型故障控制保护策略的研究［D］.北京:华北电力大学，2012.

［15］王钢，李志铿，黄敏，等.HVDC 输电系统换相失败的故障合闸角影响机理［J］.电力系统自动化，2010，34 (4):49 －54.

［16］郭春义，赵成勇，王晶.新型双馈入直流输电系统供电无源网络的运行特性研究［J］.电工技术学报，2012，27 (11):211 －218.

［17］Guo Chunyi，Zhang Yi，Gole A.Analysis of dual-infeed HVDC with LCC-HVDC and VSC-HVDC ［J］.IEEE Transactions on Power Delivery，2012，27 (3):1529 －1537.