考虑气象因子条件下的电网连锁故障预测

潘一飞，李华强，许海青，王伊渺

(四川大学 电气信息学院，四川 成都610065)

0 引 言

近年来，随着电网建设的快速发展，电网规模已经达到较高水平，但与高速发展的电网负荷和高可靠性的供电要求相比，电网结构还比较薄弱，威胁电网安全的因子比较多，特别是各种气象条件(如凝冻、雷暴、大风等)对电网运行安全的影响范围更大、程度更深，很有可能引发电网连锁故障进而导致灾难性事件的发生［1，2］。在电网实际运行中，发生恶劣天气的可能性较低，但在其影响下会导致电网内各元件出现故障的几率明显著提高，可能引发元件发生“故障聚集”现象［3］，这种现象极易引发电网连锁故障，处理不当可能造成电网大面积停电。为了准确评估常见自然灾害对线路故障率的影响，在进行电网连锁故障的预测研究时需要考虑气象因子的影响。

为了模拟电力系统连锁故障的机理，学者们提出了众多连锁故障模型，目前比较成熟的模型有:基于网络拓扑结构的连锁故障模型，如复杂网络模型［3］、无标度网络模型［4］等;基于电气元件级联失效的连锁故障模型，如级联模型［5］、分支过程模型［6］等;以及基于电网近似动态特性的连锁故障及停电模型，如最优潮流连锁故障模型［7］。

但是上述研究成果均未能将气象因子考虑到模型当中，难以适用于在复杂天气下电网连锁故障的研究，本文首先运用贝叶斯网络模型结合气象因子预测连锁故障的初始故障;其次，基于支路静态能量函数模型构建了气象因子影响下映射潮流变化的能量指标和反映电网结构脆弱性的电气介数;然后，考虑连锁故障过程中前后故障之间的累积效应，提出反映气象因子下故障后电网状态和结构的安全指标对后续故障进行预测。最后，对IEEE-57 母线系统的实例分析，验证了该方法的合理性、有效性，证明此方法预测出的连锁模式为系统中后果较严重的故障模式链(集)。

1 贝叶斯网络及支路静态能量函数模型

1.1 贝叶斯网络

贝叶斯网络是基于概率推理的图形化网络，其在解决不确定性和关联性引起的故障中有明显优势，贝叶斯网络作为一种概率网络可用于表示变量之间的依赖关系，能够图形化地表示一组变量间的联合概率分布函数［8］。贝叶斯网络由网络结构和条件概率表两部分组成，包括两个重要的独立关系性，其一是节点与他的非后代节点是条件独立的;其二是给定一个节点的马尔可夫覆盖，这个节点和网络中的所有其他节点是条件独立［9］。马尔可夫覆盖在贝叶斯网络的推理中起到非常重要的作用。

给定变量集合k=(k1，k2，… ，kn)，(k1，k2，… ，kn)表示网络中的各节点，其中k2的父节点集合parents(ki)，那么在网络中就有联合概率密度

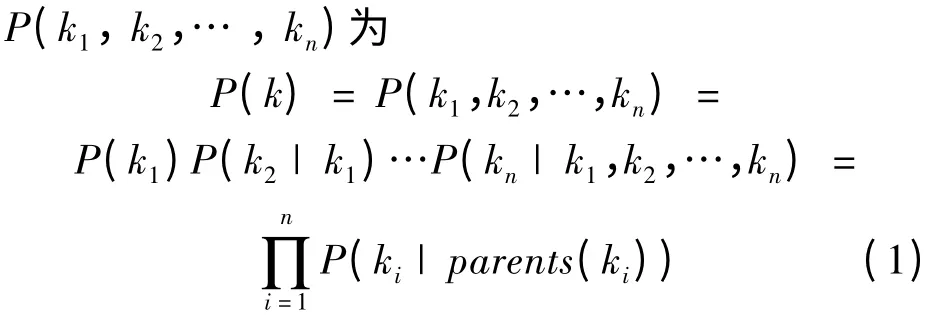
若已知集合k =(k1，k2，… ，kn)中除变量ki外其他变量的观察结果，则基于贝叶斯公式，可得出ki的条件概率为

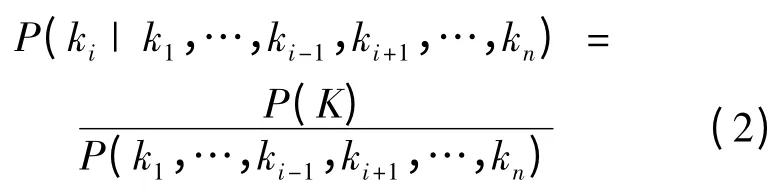
贝叶斯网络能真实的反映出大变量集合的联合概率，在计算和模拟过程中具有较高的可信度和较好的逻辑性，其结果能够更为接近真实数据，同时对数据间的因果关系有良好的体现，综合了综合先验信息和样本信息，使其既有效防范了先验信息所造成的主观偏见，也能防范样本信息造成的噪音影响。

1.2 线路的电气介数

线路中的电气介数和加权介数一样，也可以识别关键线路，两种介数都能在电力系统中反映较高介数的节点或支路，这些节点或支路的故障对电网必然有较大影响［10］。两种介数相互比较发现:加权介数主要适用在电信网信息交换当中，电气介数更加适用于电力网功率交换。定义线路(i，j)的电气介数Be(i，j)［11］:

式(3)中:电气介数Be(i，j)表示从发电节点到负荷节点的潮流对线路的利用情况;G 和L 表示系统内的全部发电节点和负荷节点的集合;Wm表示发电节点(m)的权重，一般情况下选用其实际出力或额定容量;Wn表示负荷节点(n)的权重，一般情况下选用峰值或实际负荷;Imn(i，j)为“发电－负荷”节点对(m，n)间，加上单位注入电流之后，在线路(i，j)上引起的电流。式(3)较为全面的分析了在不同发电节点和负荷节点的权重的情况，电气介数Be(i，j)能够有效体现出发电节点出力和负荷水平对线路关键性的影响，即发电容量或负荷水平较小的“发电-负荷”节点对，其对各线路电气介数影响的权重不会很大，这也更符合电力系统的实际。

1.3 支路静态能量函数模型

文献［12］建立节点能量函数模型，而本文构造了能够反映出电网支路潮流的变化在能量积累的映射的支路静态能量函数模型。电网支路模型如图1 所示，支路ij 上阻抗简化为R +jx，线路对地导纳简化为两端对地导纳j(B/2)。

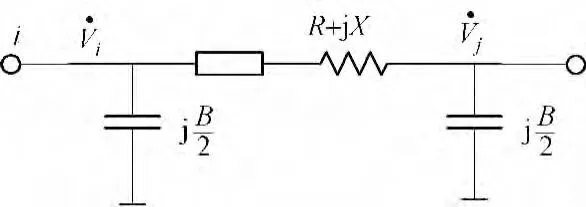
图1 电网支路简化电路Fig.1 Network branch simplified circuit

如图1 的支路模型，根据支路功率传输关系，支路ij 的潮流表达式为［13］

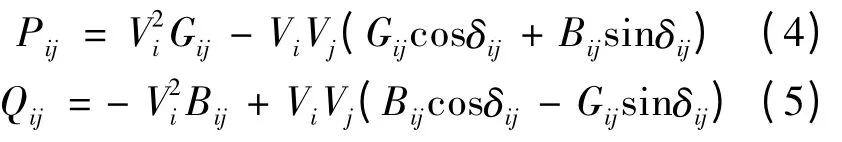
式(4)、(5)中:Pij，Qij，Bij，Gij分别表示支路ij 上的有功功率、无功功率、电纳和电导。支路能量不仅仅包括在系统运行状态下支路上的有功功率对应的能量，也包括在相同状态下同一时刻支路上的无功功率对应的能量。电网运行时，支路首末两段的电压相角差决定了有功功率，而首末两段的的幅值差则能够决定了支路上的无功功率。由此，若将电压的相角差和幅值差同时积分，即可求支路静态能量函数［14］，其表达式:

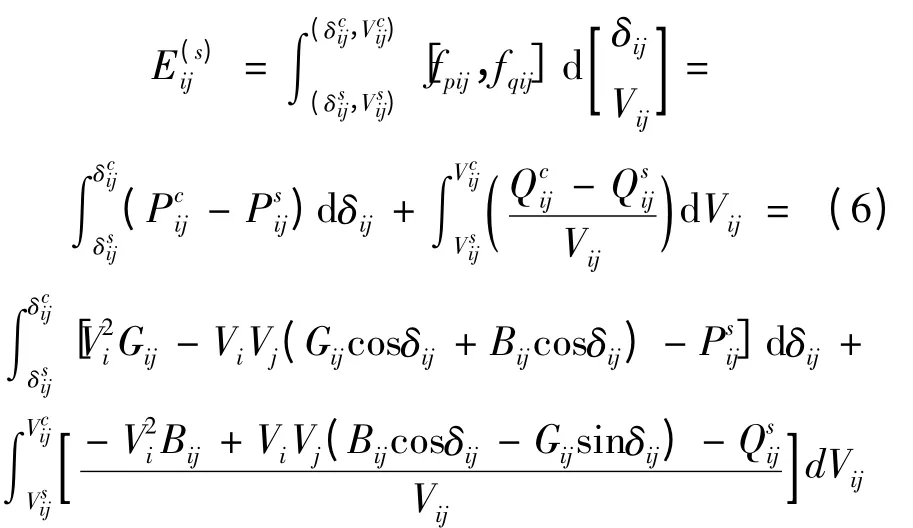
式(6)中:表示支路ij 在s 级故障后由稳态到临界状态积累的静态能量Pij，Qij的初始状态值的临界状态值。

按照SA指数的25%、50%、75%分位数，将公司面临的融资约束分为4个等级。统计所有公司在观测年度内的等级变化情况，计算每个企业最高等级与最低等级的跨度。跨度为0级的企业占企业总数的44.37%，跨度为1级的企业占比50.29%，跨度超过1级的企业占比5.34%。统计结果显示噪音较少，企业融资约束程度并没有发生频繁变化，SA指数分类结果稳定。

2 气象因子对电网的影响

电网的“故障聚集”现象极易造成电网的连锁故障，处理不当会引发电网大面积停电。为了准确评估常见自然灾害对线路故障率的影响，在进行电网连锁故障的预测研究时需要考虑气象因子的影响［15］。文献［16］认为在IEEE 346 标准中的气象因子可归为正常和恶劣两种情况，在一般情况下不对电气元件产生影响或使电气元件发生故障的可能性较小的天气可认为其是正常天气，而导致电气元件发生故障的可能性较高的天气可认为其是恶劣天气。

通过分析电网分区结构和历史气象灾害的分布、强度、影响情况，得到电网处于恶劣气象因子下元件故障率分析的实际电网结构模型，得出恶劣气象因子对电网元件故障率的影响。图2 表示在一个周期T 内的天气随机变化情况，λ′ 为在恶劣天气影响下电气元件发生故障的期望值，ai则表示这种天气的时间;λ 在正常天气影响下电气元件发生故障的期望值，ni为其时间。这样就将复杂条件下的天气变化简化为正常和恶劣天气两种天气情况的随机过程。由此可以整理得到如图3 所示，在一个周期T 的两种天气条件影响下的时间比列的关系。

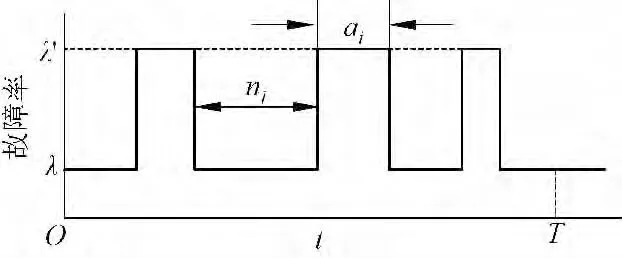
图2 天气随机变化图Fig.2 Random variation of weather

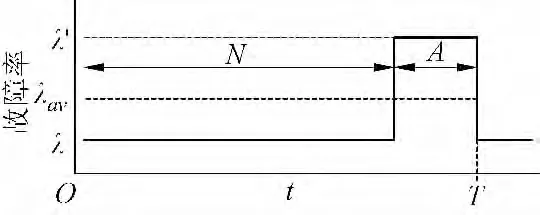
图3 周期内双态天气持续时间比例Fig.3 Proportion of cycle binary weather

在正常天气条件下的时间比例N 为

在恶劣天气条件下的时间比列A 为

根据式(7)、(8)，可以将天气影响的造成的电气元件的故障率折算成以年为单位其发生故障的次数。那么以1年为单位时线路(如图3)可以表示为

在实际电网运行时，统计和计算λ 和λ′ 是一件非常困难的事情，而本文只需要通过统计和计算λav以及故障发生在恶劣天气的百分比F，并根据式(9)得到λ 和λ′:

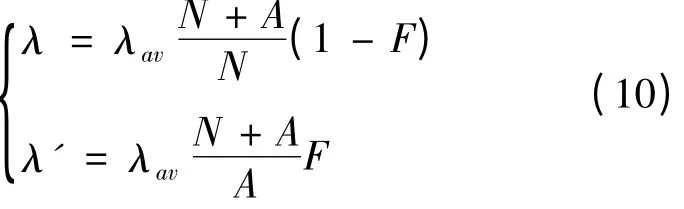
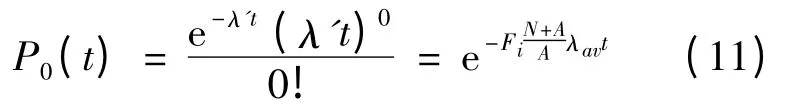
其发生故障的概率为

电网中支路P(t)值越大则该线路发生故障的可能性就越大，就越可能成为造成电网连锁故障的初始故障支路。在发生如凝冻、雷暴、大风、山火等恶劣天气时会导致电网的故障率激增，引发系统潮流改变，电网将趋向于亚稳定或边界稳定，任何小的扰动都有可能导致大停电事故的发生。

3 连锁故障预测指标的构建

3.1 综合裕度指标的构建

电网运行状态划分为3 类，即安全、临界和风险状态。由式(6)表示:当电网的运行状态发生变化时，支路ij 上的功率表示从当前运行状态到临界运行状态对应的能量积累，即E(s)ij可表征系统的能量裕度，其值越小表示支路距离临界点越近，该支路越容易成为故障支路。式(3)中的电气介数Be(i，j)反映出支路在电网拓扑结构上的权重，在气象因子影响下电气介数越大的支路发生故障后对系统的影响也就越大。本文为更加快速、准确的反映出气象因子引起电网潮流和拓扑结构的改变，将反映恶劣气象因子条件下电网结构的电气介数作为结构因子加权于线路的能量裕度，相当于对气象因子影响下的能量裕度(状态脆弱度)进行有效放大，即可得系统处于气象因子影响下支路的结构和状态脆弱度指标β(s)ij:

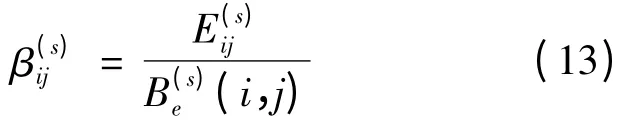
式(13)中:Eij(s)，Be(s)(i，j)为第s 级故障后支路ij的能量差值Eij和电气介数Be(i，j)。考虑到电网发生连锁故障时前后故障级间的相互影响，可分别得到支路ij 在第s 级故障后的恶劣气象因子影响下脆弱度指标Qs，s，第s－1 级故障对第s 级故障的脆弱度指标的影响因子Qs，s－1以及第s －2 级对第s 级故障的脆弱度指标的影响因子Qs，s－2:

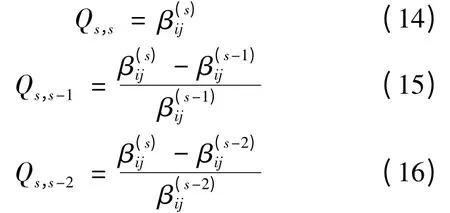
由式(14)、(15)、(16)，在气象因子影响下并计及前级故障的累积效应，当电网发生了第s 级故障后，可以由式(17)有效预测第s +1 级的故障线路:

式(15)中:Kij(s+1)表示系统发生s 级故障后，分别反映系统的故障前、故障发生过程中和故障后电网的运行状态及电网结构的安全指标，此指标预测出来的连锁模式为系统较严重的故障模式。

3.2 模型仿真算法

本文提出反映电网在气象因子影响下故障后状态和结构的安全指标，并对连锁故障的后续故障进行预测的仿真过程，包括在气象因子影响下快速计算各条线路的临界系数，对电网连锁故障中初始故障的预判、连锁故障发展过程中综合反映气象因子影响下的电气介数和电网潮流、电压及负荷变化的安全指数的计算的仿真。

当系统在恶劣气象因子影响下发生初始故障后，通过该指标搜索下一级故障，同时检测是否达到了搜索深度(本文将搜索深度设为5 级)。根据以上方法，即为得到电网遭受恶劣气象因子影响下电力系统的连锁故障的传播路径。并根据不同初始故障所造成的不同传播路径得到整个系统引发连锁故障的薄弱环节，给甄别气象因子影响下电网危险环节提供了重要依据，算法流程图如图4。

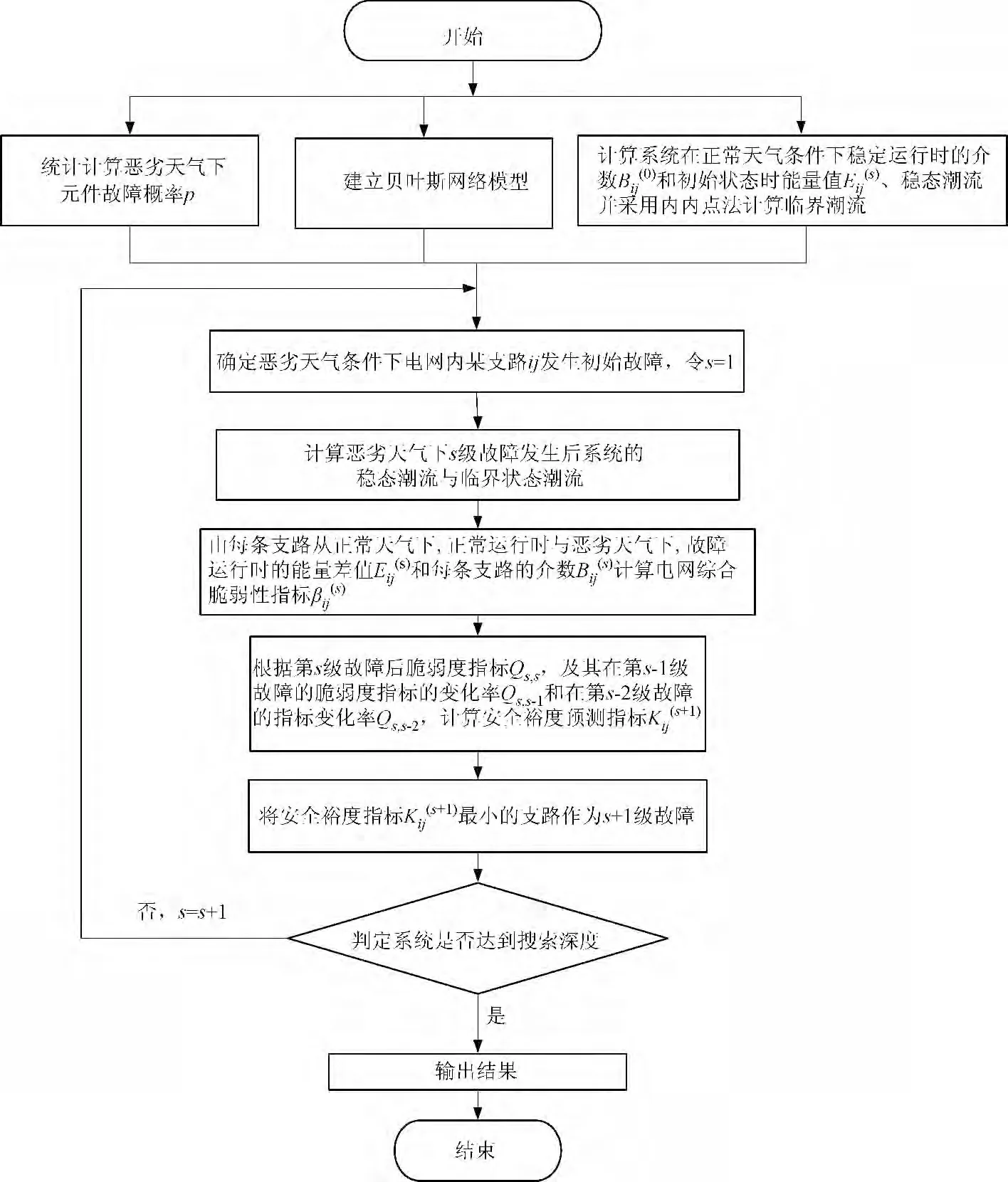
图4 模型仿真流程图Fig.4 Simulation flow chart of failure propagating model

4 算例分析

通过气象因子的影响对在IEEE-57 母线系统中验证本文方法的性能。IEEE-57 母线系统的拓扑图如图5 所示，本文支路依照除去变压器支路剩余的63 条支路编号。

该电网在恶劣气象因子的影响下，会导致元件故障率上升，导致系统潮流发生改变，进而引发线路的安全指标减小，可能造成电网发生连锁故障。图6 为IEEE-57 母线系统在气象因子影响下初始故障前的电气介数，其值越大，说明该支路故障对系统的影响越大。

由式(10)可知电网中支路P(t)值越大则该线路发生故障的可能性就越大，就越可能成为造成电网连锁故障的初始故障支路，将此概率指标和气象因子影响下未发生故障时支路ij 的结构和状态安全指标进行综合分析，得到如图7 中IEEE-57 母线系统在气象因子影响下支路初始故障率，其值越大，反映此支路在气象因子发生初始故障的可能性越大。表1 是将由图7 中所得到的IEEE-57 母线系统在气象因子影响下支路初始故障率最高的7条支路作为初始故障支路，通过仿真得到的后续故障的支路及其指标。本文将支路L43 作为初始故障支路，并对由其引发的连锁故障的模式(L43-L23-L56-L16-L12)的合理性进行分析。

图5 IEEE-57 母线系统拓扑结构图Fig.5 IEEE-57 bus system topology structure

图6 IEEE-57 母线系统在气象因子影响下故障前的电气介数Fig.6 Electrical interface number of IEEE-57 bus system under the weather factor influence before failure

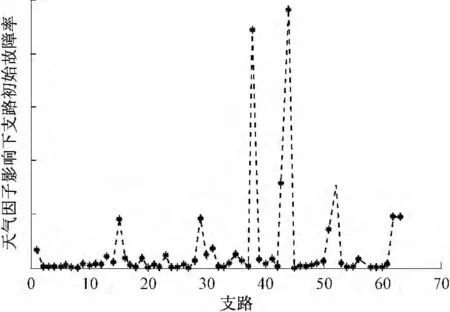
图7 IEEE-57 母线系统在气象因子影响下支路初始故障率Fig.7 Branch initial failure rate of IEEE-57 bus system under the weather factor influence

在IEEE-57 母线系统中，由于恶劣气象条件引发支路L43 发生初始故障并退出运行，引发系统潮流改变，造成电网其他线路的安全指标Kij(s+1)的值减小。在发生第一级故障后，由稳态到临界态的安全裕度L23 只有0.007 731 2，综合

性指标为－0.922 88，为所有支路指标中最小的值，所以二级故障最后可能出现在连接发电机节点的支路L23 上。预测三级故障时，由于系统发生前两级故障后潮流大量转移在L56 上，抬高了稳态潮流值，也就间接缩短了稳态与临界态的距离。由于计及气象因子并结合电网本身的结构脆弱性，在考虑到第一、二级对第三级故障的影响，求得第三级故障支路L56 的综合性指标为－1.954，其为系统内各支路指标的最小值。而第四、五级故障支路L16，L12 与以上故障相似，均为连接或靠近重要发电节点或重要负荷节点的支路。当靠近初始故障的L12 支路发生故障后，达到搜索深度，搜索结束。

对IEEE-57 母线系统中所有由恶劣天气引发的电网连锁故障的初始故障支路进行模拟仿真，并通过这些初始故障对电力系统的后续故障进行预测后，得到系统严重故障模式链(集)，同时可以得到如下规律:

(1)例如支路L16，L12 连接重要发电机、负荷和长程连接的支路对故障传播影响较大。

(2)越靠近故障点的支路的潮流变化越明显，在故障点附近的支路更容易发生故障。

另外，连锁故障过程中电网可能会逐渐逼近临界状态，在这过程中继电保护装置动作几率增大，因此系统中保护装置发生误动和拒动的概率也相应增加，这也是连锁故障的机理之一。

5 结 论

由于气象因子影响下连锁故障初始故障发生的复杂性与特殊性，运用贝叶斯网络模型结合气象因子能够更加精准确定在天气影响下电网的初始故障。通过建立完整的支路静态能量函数的模型和反映气候影响下电网故障后状态和结构的综合安全指标，对电网的后续故障进行预测。本文提出的仿真算法得到的故障模式链即为连锁故障传播的路径。通过对系统较严重的故障模式集的分析，得出气象因子造成的连锁故障过程中有意义的规律性结论，对预防恶劣天气下电网的锁故障事故的有一定的指导意义。

［1］孟仲伟，鲁宗相，宋靖雁.中美电网的小世界拓扑模型比较分析［J］.电力系统自动化，2004，28(15):21 －24.

［2］顾雪平，张硕，梁海平.考虑系统运行状况的电网连锁故障风险性评估［J］.电力系统保护与控制，2010，38 (24):124 －130.

［3］孙可，曹一家，韩祯祥.复杂电网连锁故障模型评述［J］.电网技术，2005，29 (13):1 －8.

［4］Chassin D P，Posse C.Evaluating north American electric grid reliability using the Barabasi-Albert network model ［J］.Physica A，2005，355 (2 －4):667 －677.

［5］Dobson I，Carreras B A，Newman D E.A probabilistic loading-dependent model of cascading failure and possible implications for blackouts ［C］.Proceedings of the 36th Annual Hawaii International Conference on Systems Sciences.Maui，USA:IEEE，2003:10－19.

［6］Dobson I，Wierzbicki K R，Kim J，et al.Towards quantifying cascading cascading blackout risk ［C］.Bulk Power System Dynamics and Control.Hawaii，USA:IEEE，2007:1 －12.

［7］梅生伟，翁晓峰，薛安成.基于最优潮流的停电模型及自组织临界性分析［J ］.电力系统自动化，2006，30 (13):1 －5.

［8］Przytula K W，Thompson D.Construction of Bayesi-an networks for diagnostics ［A］.In:Proceedings of IEEE Aerospace Conference ［C］，2000，5:193 －200.

［9］史会峰，谷根代.基于MCMC 算法贝叶斯网络的学习［J］.华北电力大学学报，2004，31 (4):109－112.

［10］Kinney R，Crucitti P，Albert R，et al.Modeling cascading failures in the North American power grid ［J］.The European Physical Journal，2005，46 (1):101－107.

［11］徐林，王秀丽，王锡凡.基于电气介数的电网连锁故障传播机制与积极防御［J］.中国电机工程学报，2010，30 (13):61 －68.

［12］刘慧，李华强，郑武.基于电压脆弱性的支路事故排序快速算法［J］.电力系统保护与控制，2010，38 (23):177 －181.

［13］郑武，李华强，刘慧.基于静态能量函数法的电压弱节点分析［J］.电力系统保护与控制，2010，38(14):79 －83.

［14］刘群英，刘俊勇，刘起方.基于支路势能信息的电网脆弱性评估［J］.电力系统自动化，2008，32(10):6 －11.

［15］王佳明，刘文颖，张建立.恶劣天气下的复杂电网连锁故障在线预警［J］.电网技术，2012，36(5):239 －244.

［16］刘文颖，杨楠，张建立.计及恶劣天气因素的复杂电网连锁故障事故链模型［J］.中国电机工程学报，2012，32 (7):53 －59.