一种采用双混沌搜索的类电磁机制算法

姜建国,刘梦楠,刘永青,苏 仟,张丽媛

(西安电子科技大学计算机学院,陕西西安 710071)

一种采用双混沌搜索的类电磁机制算法

姜建国,刘梦楠,刘永青,苏 仟,张丽媛

(西安电子科技大学计算机学院,陕西西安 710071)

针对现有算法中初始种群随机性强、局部搜索能力差、移动公式效率低等问题,提出了一种改进的类电磁机制算法.结合反向学习理论,引入带扰动因子的反向学习机制构造初始种群;提出了一种双混沌优化机制用于局部搜索;运用改进后的公式计算粒子之间的合力;设计了一种自适应移动算子来更新粒子.实验结果表明,改进后的算法具有更好的收敛效果和更高的求解精度.

类电磁机制算法;反向学习机制;扰动;双混沌;全局优化

在求解实际问题时,一般建立的数学模型要么维数高,要么没有好的解析性质或难以获知解析性质,因此确定全局优化算法很难或不能求解这些问题.随机搜索算法的出现为这类问题的求解提供了新的思路.作为一种随机搜索算法,类电磁机制(Electromagnetism-like Mechanism,EM)算法[1]模拟了电磁场中带电粒子之间的吸引排斥机制,通过该机制使得粒子朝着最优粒子移动,已成功用于求解全局优化问题.该算法具有寻优机制简单、搜索能力强、所需资源少、收敛速度快等优点.但是,标准类电磁机制算法中,初始种群是随机产生的,多样性不够丰富;局部搜索范围小,形式单一,易陷入早熟收敛;粒子间距离对其相互作用力影响较大,可能导致粒子寻优方向错误、计算溢出等问题;粒子的移动没有考虑到进化代数的影响,使得算法效率偏低.

为此,笔者提出了一种改进的类电磁机制算法(Improved Electromagnetism-like Mechanism algorithm,IEM),即结合反向学习理论,引入带扰动因子的反向学习机制[2]构造初始种群,既保证了初始群体含有较丰富的模式,又有利于提高整体的进化收敛速度;提出了基于双混沌优化机制的局部搜索策略,运用两种完全不同的混沌优化机制各自独立搜索,不仅避免了算法过早陷入局部最优,而且在一定程度上提高了解的精度;运用改进后的公式[3]计算粒子间的作用力,同时加入扰动粒子避免因早熟收敛而陷入局部最优;设计了新的自适应移动算子来更新粒子.实验结果表明,改进的类电磁机制算法在求解精度上有很大提高,对于经典的评价优化算法执行效果的测试函数,均取得了比较好的结果.

1 经典类电磁机制算法

类电磁机制算法的实现主要由4个阶段完成,分别是初始化、局部搜索、电荷量及力的计算以及粒子移动.具体步骤见文献[1].

2 改进的类电磁机制算法

2.1 带扰动因子的反向学习机制的初始种群的构造

反向学习是由Tizhoosh[2]提出的,之后被应用于粒子群算法[4]等多种进化算法中,取得了较好的效果.其基本思想是比较候选个体的适应度与反向个体的适应度,保留数值较小者,从而获得当前最优值.相关定义见文献[2].

为了增加粒子的多样性,提高粒子向新区域学习的能力,在反向学习算法中引入了扰动因子,即在计算xi的反向点时,随机选择一个粒子xj作为扰动粒子,给当前粒子一定的扰动,其中i≠j且i=1,2,…,n, j=1,2,…,n.带扰动因子的反向点定义为

式中,λ为(0,1)中的随机数.

笔者提出的改进算法是在进化过程中,选择一些靠近最优个体的初始粒子,从而在一定程度上可以加快算法的收敛速度.具体方法为:利用经典类电磁机制算法的初始化,随机选取n个点作为初始化粒子,在计算每个粒子的适应值的同时,计算该粒子对应的带扰动因子的反向粒子的适应值,通过两者相比较,挑选适应值更小的初始粒子作为初始种群.

2.2 采用双混沌优化机制的局部搜索

在优化设计领域中,混沌现象的遍历性特点可以作为搜索过程中避免早熟收敛的一种优化机制.虽然单个混沌优化算法能遍历可行域中的所有状态,但是需进行多次遍历搜索,且搜索次数很难确定.为了提高混沌优化的效率,笔者提出了采用双混沌优化机制的局部搜索策略,并给出了结束条件.即通过运用两种完全不同的混沌优化机制进行各自独立的搜索,丰富了搜索的动力学行为,提高了搜索的充分性.

笔者选取

和

共同作为产生混沌的机制进行优化搜索.其中,式(2)是Logistic映射,数学上已经证明μ=4时系统完全处于混沌状态;式(3)为立方映射,当a∈[3.3,4]时为混沌映射[5],经实验测试,选a=3.5.在(0,1)之间随机取一个值,以该值为初始点,利用Logistic映射和立方映射分别进行混沌迭代20次,将迭代过程中产生的混沌变量值记录下来,如图1所示.从图1中可以看出,在相同初始值、相同迭代次数的情况下,Logistic映射和立方映射的混沌变量值在绝大多数情况下都是不同的,这就为笔者提出的基于双混沌优化的局部搜索能避免陷入局部最优并提高解的精度奠定了理论基础.

基于双混沌优化的局部搜索可分为粗搜索和细搜索两个阶段.其中,粗搜索阶段可避免算法过早陷入局部最优,而细搜索阶段对当前最优粒子附加随机扰动,使得算法具有精细搜索的功能.粗搜索阶段的结果可以为细搜索提供有效的初始点,避免搜索陷入局部极小;细搜索阶段又可以弥补粗搜索在精细搜索能力方面的不足,在一定程度上提高解的精度.

笔者提出的算法只对当前最优粒子进行局部搜索操作.具体的步骤描述如下.

(1)粗搜索阶段.

步骤1 令y1=xbest,y2=xbest,其中,y1是Logistic映射的搜索变量,y2是立方映射模型的搜索变量.

步骤2 将当前最优粒子的解空间映射到两个混沌空间,即

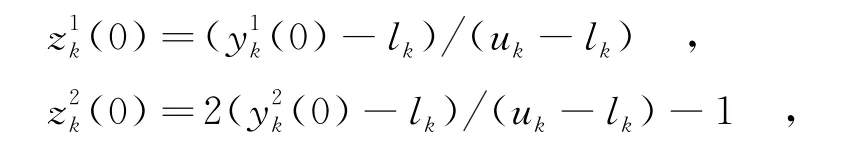
并以此作为混沌搜索的初始解.其中,z1和z2是上述两映射的混沌空间变量;k为遍历粒子各维的变量,且k=1,2,…,m.

步骤3 在局部搜索迭代次数L内,对混沌变量z1和z2进行混沌迭代,即

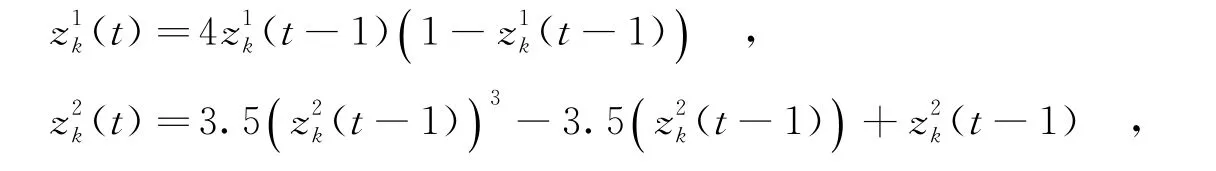
其中,0＜zk1＜1,-1＜zk2＜1;t是混沌迭代次数,且t=1,2,…,L.

步骤4 将混沌空间映射回解空间,即

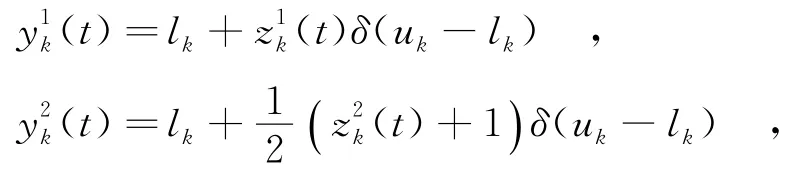
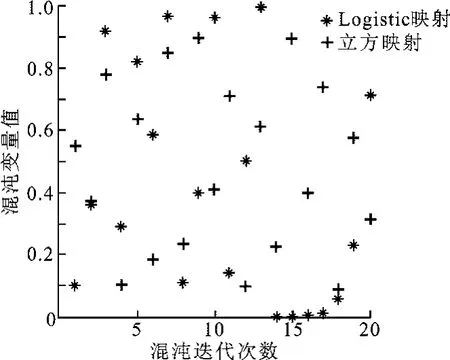
图1 Logistic映射和立方映射混沌迭代取点效果对比

其中,δ为局部搜索参数,δ∈[0,1].

步骤5 计算目标函数值f(y1)和f(y2).如果f(y1)＜f(y2)＜f(xbest),则置xbest=y1;如果f(y2)＜f(y1)＜f(xbest),则置xbest=y2;如果仅f(y1)＜f(xbest),则置xbest=y1;如果仅f(y2)＜f(xbest),则置xbest=y2;否则,转步骤3,直至满足结束条件.

(2)细搜索阶段.以粗搜索阶段找到的最优值xbest为中心,对其施加随机扰动,实施细搜索阶段,其中变量的含义与粗搜索阶段相同.该细搜索过程可描述为:

步骤1 令y1=xbest,y2=xbest.

步骤2 将当前最优粒子的解空间映射到两个混沌空间,即

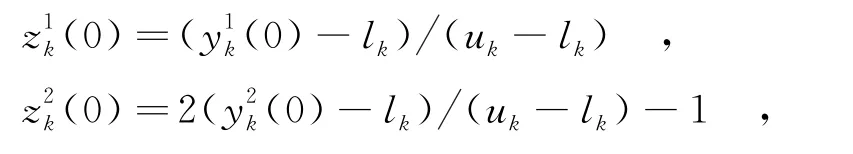
并以此作为混沌搜索的初始解.

步骤3 在局部搜索迭代次数L内,对混沌变量z1和z2进行混沌迭代,即

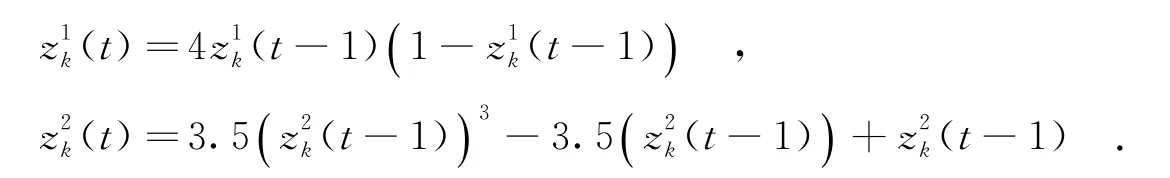
步骤4 由于z2混沌变量已处于(-1,1)区间,故此步只将z1映射到(-1,1)区间,即

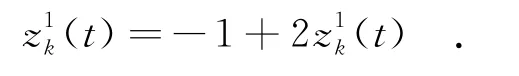
步骤5 将混沌空间映射回解空间,即

步骤6 计算目标函数值f(y1)和f(y2).如果f(y1)＜f(y2)＜f(xbest),则置xbest=y1;如果f(y2)＜f(y1)＜f(xbest),则置xbest=y2;如果仅f(y1)＜f(xbest),则置xbest=y1;如果仅f(y2)＜f(xbest),则置xbest=y2;否则,转步骤3,直至满足结束条件.

至此,基于双混沌优化的局部搜索已完成,细搜索阶段得到的计算结果xbest即为双混沌优化方法最终的计算结果.

2.3 电荷量及力的计算

在标准类电磁机制算法中,两粒子间的距离可能不利于粒子朝更优方向移动或导致计算溢出等问题.为此,笔者采用文献[3]中的方法,将目标函数值归一化,运用修正后的合力计算公式,不但不会降低最优值的精度,反而提高了算法的运行速度.

2.4 粒子的更新

在经典类电磁机制算法中,粒子的移动步长没有考虑到粒子进化代数对移动范围的影响.针对该问题,文献[6]提出了使用一个自适应的移动算子来控制移动步长的方法,但其适应度函数的下降速度偏快,使粒子容易陷入局部最优,进而无法搜索到全局最优解.

在综合考虑提高算法搜索效率并改善早熟收敛现象的情况下,笔者设计了一个自适应的移动算子,即

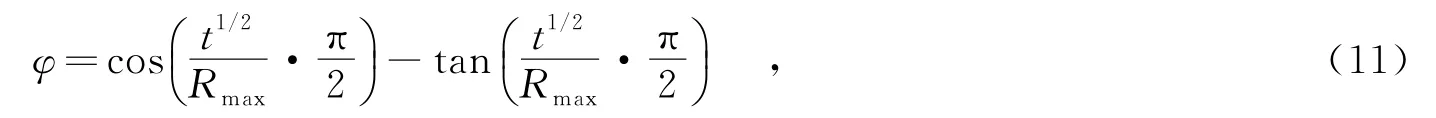
其中,t表示当前迭代次数,Rmax表示最大迭代次数.对当前迭代次数t进行开方操作的主要原因是为了避免上述余弦函数的值下降过快,进而导致算法陷入局部最优而无法跳出.

图2显示了改进的类电磁机制移动算子和文献[6]的收敛曲线对比.从图中可以看出,文献[6]中的自适应函数值下降速度较快,可能会导致算法过早陷入局部最优,进而无法搜索到问题的全局最优解.而笔者设计的移动算子的下降则相对平缓,符合粒子移动的规律.

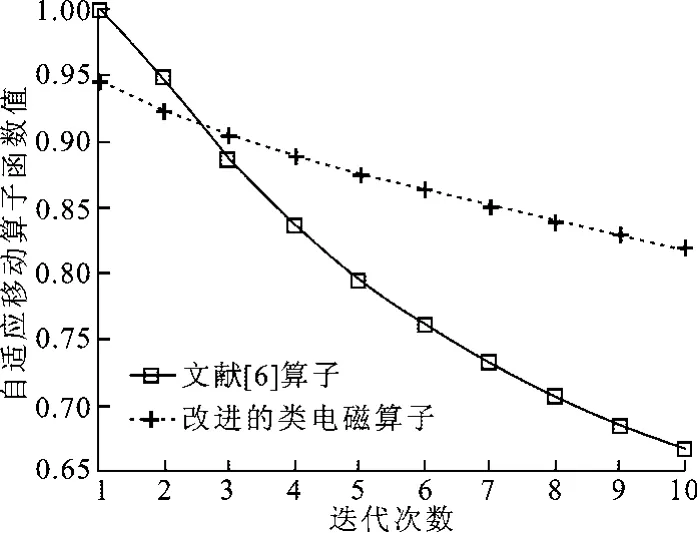
图2 改进的类电磁机制移动算子与文献[6]收敛效果对比

3 实验结果及分析

为了验证改进的类电磁机制算法的优越性,将其与文献[7]的改进算法(Electromagnetism-like Mechanism algorithm based on the Good point set,GEM)、基本类电磁机制算法进行对比.

选取了4个简单测试函数[8]、3个复杂测试函数[8]进行试验,分别运行25次,记录算法运行的最优解并计算平均值和标准差.类电磁机制算法(EM)、GEM和改进的类电磁机制算法(IEM)的仿真结果对比如表1所示.

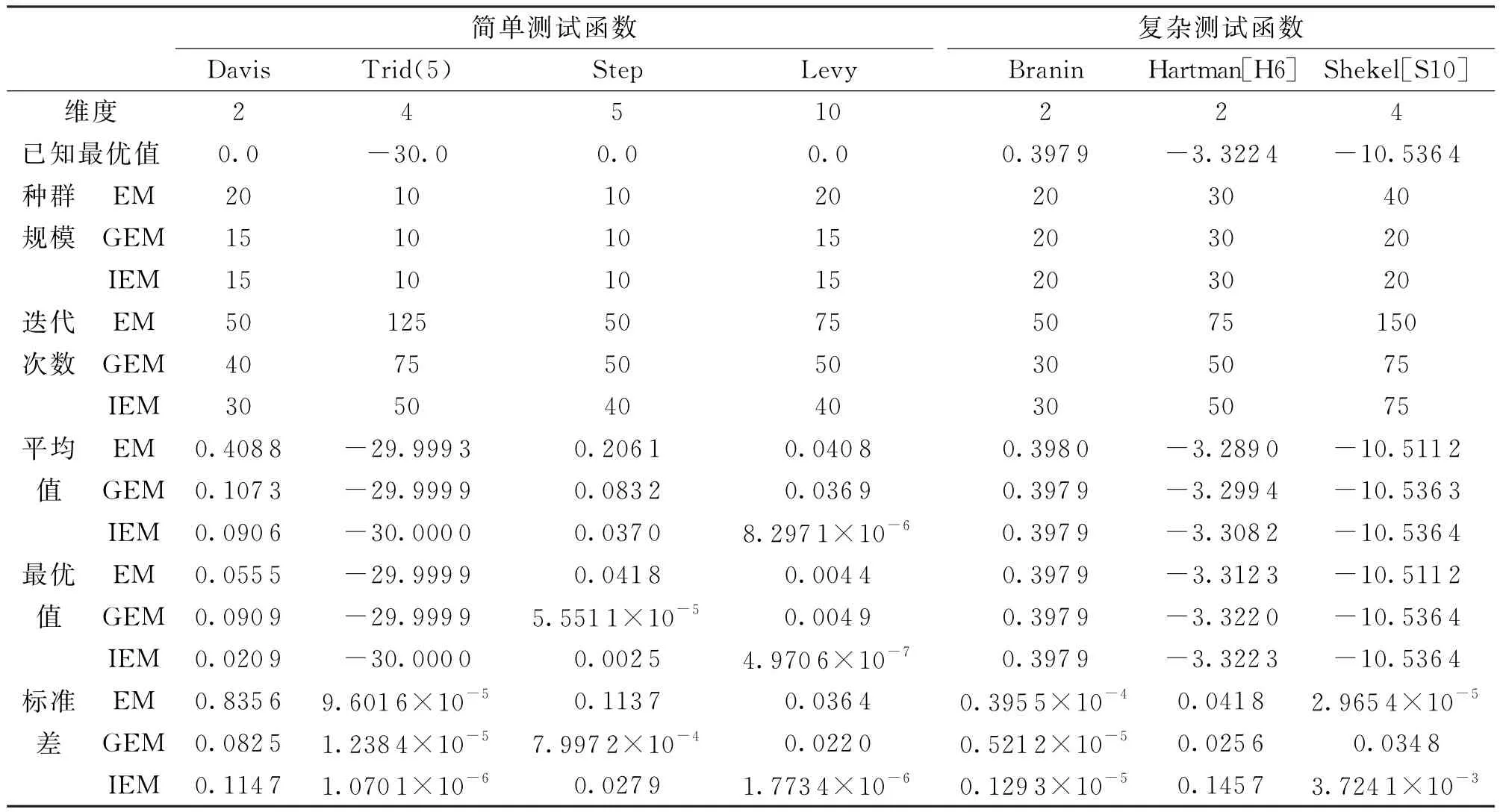
表1 仿真结果

从表1可以看出,对于Levy函数和可行域较大的Davis函数,改进的类电磁机制算法用比标准类电磁机制算法和GEM较小的种群规模和较少的迭代次数就能找到更优的全局最优值;对于Levy函数,改进的类电磁机制算法得到的解的值更加稳定;对于Trid(5)函数,改进的类电磁机制算法用较少的迭代次数求得了比标准类电磁机制算法和GEM更好的解;对于Step函数,改进的类电磁机制算法找到了不劣于标准类电磁机制算法的全局最优值;对于有多个局部极小点的Branin函数和Shekel[S10]函数,改进的类电磁机制算法均能较有效地找到它们的全局最优值;对于Hartman[H6]函数,改进的类电磁机制算法求得了比标准类电磁机制算法和GEM更好的全局最优解.

为了验证该算法能成功地用于高维函数,选取了5个典型的函数[9],分别使用标准类电磁机制算法(EM)、GEM和改进的类电磁机制算法(IEM)进行了仿真,并对仿真结果进行了比较.其中,5个函数的维度均为30,种群规模分别为40、10、10、10、10,最大迭代次数分别为500、1 000、1 000、1 000、1 000,分别运行20次,测试结果如表2所示.

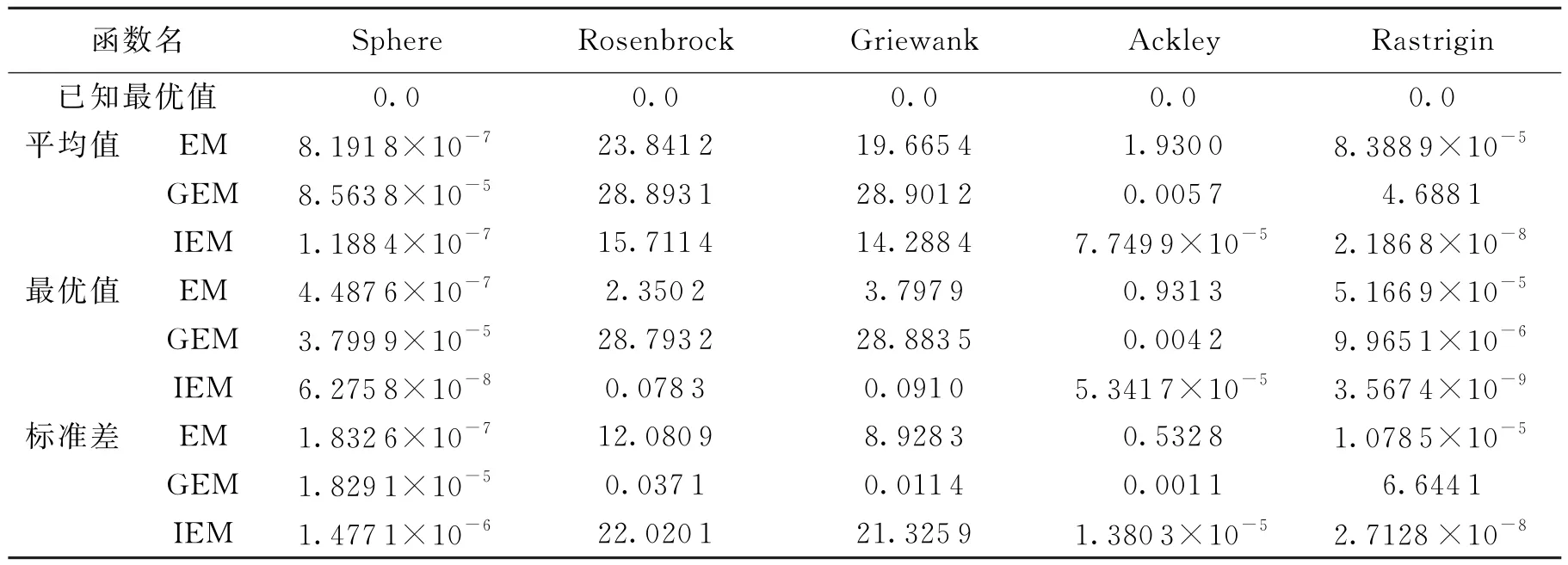
表2 高维函数测试结果

表2验证了改进的类电磁机制算法可成功用于不可微、高维、多峰甚至是病态的函数,不仅求得了这些函数的全局最优值,也明显地提高了解的精度.

4 结束语

从类电磁机制算法的机理出发,分析了其优化原理.针对原算法中存在的随机生成初始种群多样性差、局部搜索随机性强、移动公式效率低等问题,提出了一种改进的类电磁机制算法.通过引入带扰动因子的反向学习机制构造初始种群,提高了算法的搜索性能;采用双混沌优化机制作为局部搜索策略,有效地避免了算法的早熟收敛,并使算法能得到更精确的全局最优解;最后,考虑了进化代数影响,设计了新的自适应移动算子,提高了算法的寻优效率.仿真结果表明,改进的类电磁机制算法在求解无约束优化问题时,在解的精度上取得了比标准类电磁机制算法和GEM算法更好的效果,平均提升20%～30%.针对高维复杂函数,该算法在寻优速度方面还有待改进.

[1]Birbil S,Fang S C.An Electromagnetism-like Mechanism for Global Optimization[J].Journal of Global Optimization, 2003,25(3):263-282.

[2]Tizhoosh H R.Opposition-based Learning:a New Scheme for Machine Intelligence[C]//Proceedings of International Conference on Computational Intelligence for Modeling,Control and Automation.Piscataway:IEEE,2005:695-701.

[3]王双记.类电磁机制算法的改进与应用[D].西安:西安电子科技大学,2012.

[4]Wang H,Liu H,Liu Y,et al.Opposition-based Particle Swarm Algorithm with Cauchy Mutation[C]//IEEE Congress on Evolutionary Computation.Piscataway:IEEE,2007:4750-4756.

[5]修春波,刘向东,张宇河.双混沌机制优化方法及其应用[J].控制与决策,2003,18(6):724-726. Xiu Chunbo,Liu Xiangdong,Zhang Yuhe.Optimization Algorithm Using Two Kinds of Chaos and Its Application[J]. Control and Decision,2003,18(6):724-726.

[6]龙秀萍.类电磁机制算法研究[D].西安:西安电子科技大学,2012.

[7]姜建国,龙秀萍,田旻,等.一种基于佳点集的类电磁机制算法[J].西安电子科技大学学报,2011,38(6):167-172. Jiang Jianguo,Long Xiuping,Tian Min,et al.Electromagnetism-like Mechanism Algorithm Based on the Good Point Set [J].Journal of Xidian University,2011,38(6):167-172.

[8]韩丽霞.自然启发的优化算法及其应用研究[D].西安:西安电子科技大学,2009.

[9]Wang Yuping,Dang Chuangyin.An Evolutionary Algorithm for Global Optimization Based on Level-set Evolution and Latin Squares[J].IEEE Transactions on Evolutionary Computation,2007,11(5):579-595.

(编辑:郭 华)

Electromagnetism-like mechanism algorithm via dual chaotic search

JIANG Jianguo,LIU Mengnan,LIU Yongqing, SU Qian,ZHANG Liyuan
(School of Computer Science and Technology,Xidian Univ.,Xi’an 710071,China)

An improved Electromagnetism-like mechanism algorithm is proposed to overcome the drawbacks of the original EM algorithm,such as strong randomness of the initial population,low ability for local search and low efficiency in the movement according to the total force.The new algorithm generates the initial population with the disturbance factor and opposite learning mechanism,improves the local search algorithm with the double chaotic search method,and calculates the total force between particles with the modified equation.Besides,the algorithm is used to design an adaptive move operator for updating the locations of those particles.Experimental results indicate that the proposed algorithm has a better convergence effect and a higher solution accuracy.

electromagnetism-like mechanism algorithm;opposite learning mechanism;disturbance;dual chaotic search;global optimization

TP301.6

A

1001-2400(2014)05-0079-05

2013-03-12< class="emphasis_bold">网络出版时间:

时间:2014-01-12

国家部委基础科研计划资助项目(A1120132007)

姜建国(1956-),男,教授,E-mail:jgjiang@mail.xidian.edu.cn.

http://www.cnki.net/kcms/doi/10.3969/j.issn.1001-2400.2014.05.014.html

10.3969/j.issn.1001-2400.2014.05.014