混凝土泵车臂架结构的受力分析
2014-07-25卫良保龚桂良司炎飞万小平
卫良保,龚桂良,任 鹏,司炎飞,万小平
(1.太原科技大学机械工程学院,山西太原 030024;2.湖南水口山有色金属集团有限公司,湖南衡阳 421513)
混凝土泵车是集输送成品混泥土和浇筑工序于一体的建筑机械,在将预拌好的混凝土输送到模板的过程中,可连续、均匀、快速地输送,使混凝土不易离析,质量得以保证,是现代建筑不可缺少的工程机械[1-3].文献[4 -6]将各节臂自重简化为集中载荷作用于中点,且不考虑管力的作用,但没有分析这种简化所带来的影响.文献[7]对混凝土泵车臂架结构进行了非线性计算,虽给出了非线性计算与线性计算结果之间的差距,但没有评价哪种方法更为合理.本文分四种常用设计情形进行讨论,建立了臂架弯矩、铰支力和扭矩的数学计算模型和解析计算公式,并利用相关软件针对四种设计情形进行求解.
1 建立臂架数学模型[4,6,8]
1.1 臂架受力分析
取整个臂架作为研究对象,受力情况如图1所示.可以将整个臂架视为一个刚体,依照臂架连接的状况,将五个节臂当成铰接在基座之上的悬臂梁.五个节臂简化为按线性变化的渐变形梁,且前一节臂小端与后一节臂大端的均布载荷相等,均布载荷端点值为q1,q2,q3,q4,q5和q6.各节臂上的管力由焊接在节臂与混凝土管之间的四根连接杆支撑,为了简化,假设管力只由节臂的一根连接杆支撑,且作用在对应节臂的中点,则根据力的平移定理将其平移到节臂各铰接点的连线上时,会在每个节臂的中点产生一个集中载荷和一个扭矩,图1 中F1,F2,F3,F4,F5和T1,T2,T3,T4,T5即为管力分别在节臂1至节臂5上产生的集中载荷和扭矩,F6为臂架末端软管及其内部混凝土质量产生的载荷.

图1 臂架受力分析图Fig.1 Stress analysis diagram of boom structure
由静力平衡原理可知

其中,
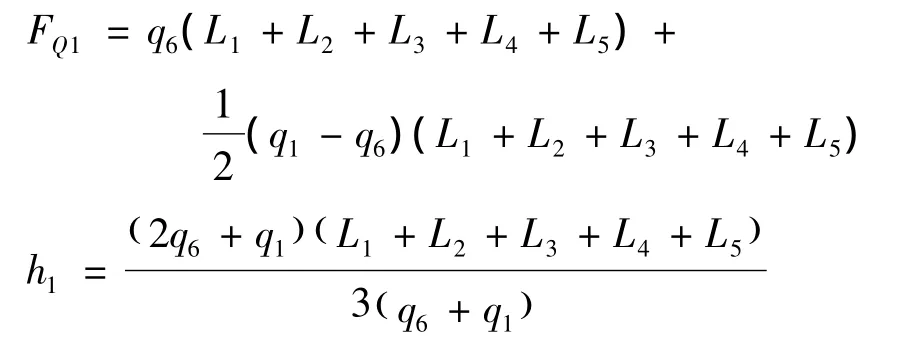
式中:FB为节臂1驱动油缸力,FAx和FAy为铰点A的铰支力,FQ1为五个节臂的重量和,h1为五个节臂形心坐标在x轴方向的长度.
联立方程(1)~(3)便可求得FB,FAx和FAy的值.类似地,可以求出节臂4至节臂5上各铰接点的力.
1.2 直杆四连杆机构1受力分析
在图1中,直杆四连杆机构1连接节臂1和节臂2,节臂2依靠直杆四连杆机构1中油缸的伸缩而改变其俯仰角度以达到所需工况的目的,其中杆DS1和ES2为二力杆,取直杆四连杆机构1作为研究对象,受力情况如图2所示.

图2 直杆四连杆机构1受力分析图Fig.2 Loading analysis diagram of straight-bar four-bar linkage 1
由静力平衡原理可知
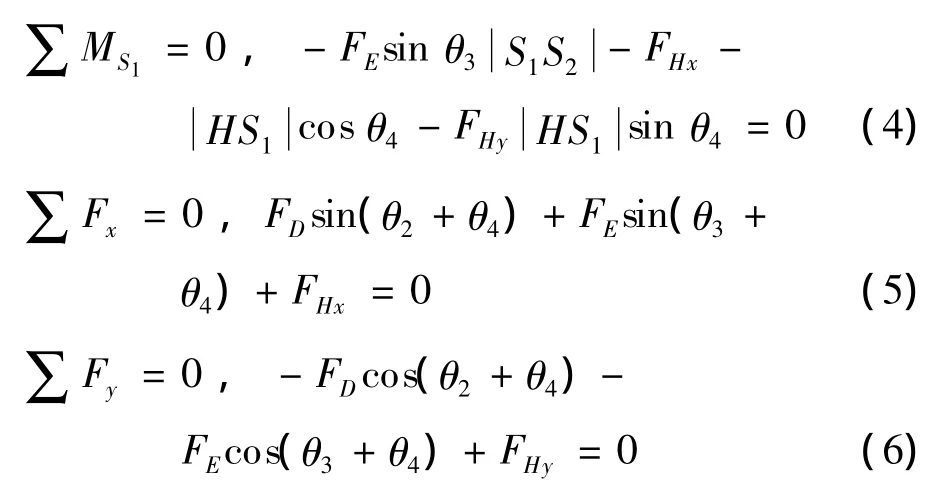
式中:FD为节臂2驱动油缸力,FE为连杆ES2所受压力,FHx和FHy为铰点H所受铰支力.
此方程组只有三个方程,却有四个未知数,属于超静定问题,与节臂2的平衡方程联立便能求解出未知数FD,FE,FHx和FHy.类似地,可以求出另一个直杆四连杆机构铰接点的力.
1.3 弯板四连杆机构1受力分析
取弯板四连杆机构1作为研究对象,受力情况如图3所示.由静力平衡原理可知,
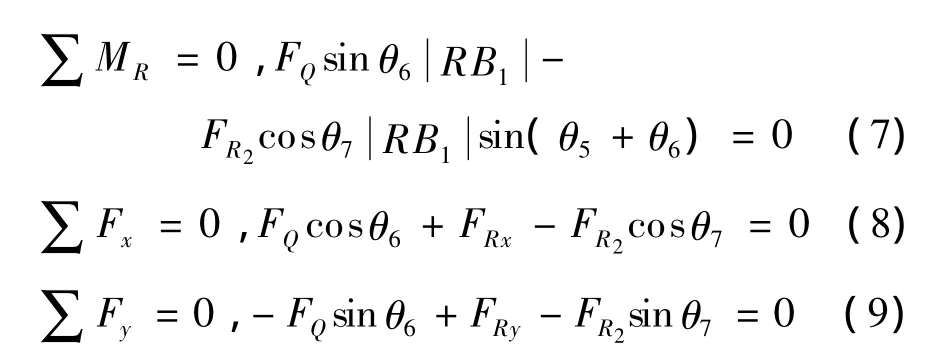
式中:FQ为节臂4驱动油缸力;FR2为连杆R2B2所受压力,FRx和FRy为铰点R所受铰支力.
此方程组只有三个方程,却有四个未知数,属于超静定问题,与节臂4的平衡方程联立便能求解出未知数FQ,FR2,FRx,FRy.类似地,可以求出另一个弯板四连杆机构铰接点的力.

图3 弯板四连杆机构1受力分析图Fig.3 Loading analysis diagram of angleblock four-bar linkage 1
2 建立弯矩、剪力和扭矩数学模型[8]
取长度为xF6的节臂5右段作为研究对象,受力情况如图4所示.
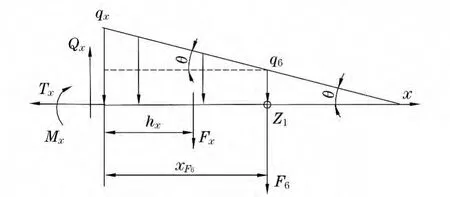
图4 节臂5结构弯矩和扭矩分析图Fig.4 Analysis diagram of bending mom ent and tw isting moment of boom 5
图4中为0≤xF6≤|ZZ1|的情形,由静力平衡原理可知,
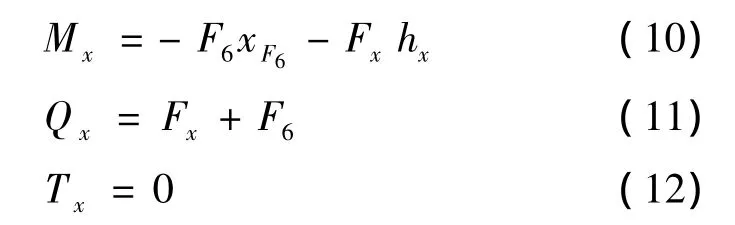
其中,

式中:Tx,Mx,Qx和qx分别为所取截面的扭矩、弯矩、剪力和均布载荷;Fx为节臂5的重量;hx为节臂5形心到所截截面的距离.
类似地,可以求出其他节臂的弯矩和扭矩.需要指出,当x取在节臂3,4,5上时,取其横截面的右边部分进行计算;当x取在节臂1,2上时,取其横截面的左边部分进行计算,这样可以简化计算.
3 计算各节臂铰接力
3.1 计算方法
分四种情形计算:情形1考虑管力,将臂架重量视为均布力;情形2考虑管力,将臂架重量视为均布力,利用Matlab计算解析解;情形3不考虑管力,将臂架重量视为均布力;情形4不考虑管力和液压缸四连杆机构等重量,而且将臂架重量视为集中力作用于各节臂中点,情形1,3,4均利用Solid-Works有限元求解,再利用其“列举销钉力”工具求出各铰支力.
3.2 计算结果
为了更直观地分析四种情形,绘制出四种情形下的剪力、铰支力和弯矩对比图,如图5所示.铰接点编号 0 -9 分别对应铰接点A,B,D,E,G,H,K,K1,N1,N.图6为情形1的臂架应力云图.
3.3 结果分析
3.3.1 相对误差分析
(1)如图7a所示,情形2相对情形1在铰接点N1处产生最大相对误差为15%,情形3相对情形1在铰接点A处产生最大相对误差296%,情形4相对情形1分别在铰接点E,G,H,K1处达到最大相对误差99%.
(2)如图7b所示,情形2相对情形1在铰接点A处产生最大相对误差5%,情形3相对情形1在铰接点A处产生最大相对误差388%,在铰接点B,D和E处分别产生相对误差98%,100%和97%,情形4相对情形1在各铰接点相对误差都超过98%,在铰接点D和E处达到最大相对误差100%.
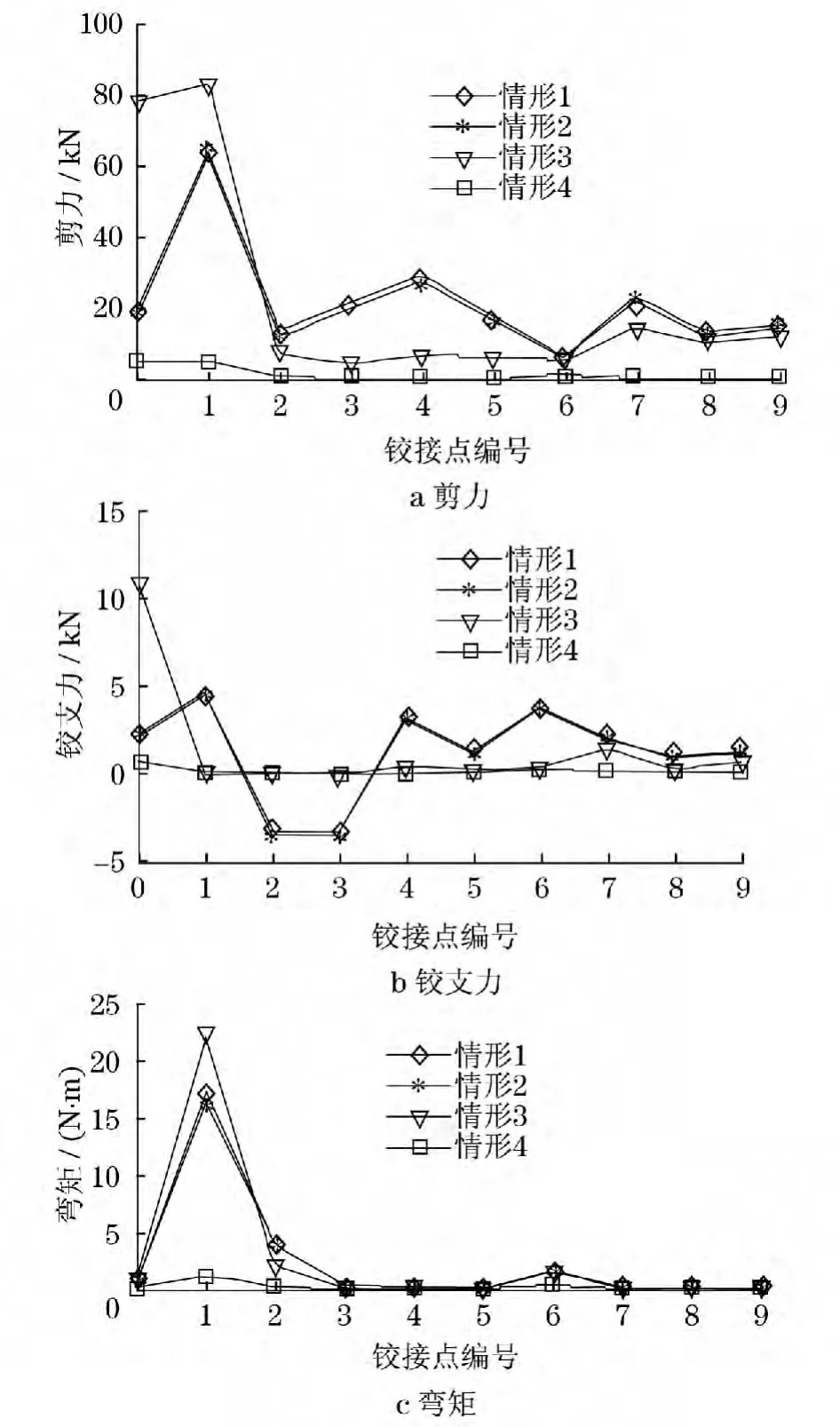
图5 四种情形下剪力、铰支力,弯矩对比图Fig.5 Com parison of shearing force,hingesupported force and bending moment under four situations

图6 臂架应力云图(情形1)Fig.6 M ises stress nephogram of boom structure(situation 1)
(3)如图7c所示,情形2相对情形1在铰接点H处产生最大相对误差11%,情形3相对情形1在铰接点A处产生最大相对误差511%,在铰接点E,G和K1处分别产生相对误差82%,77%和74%,情形4相对情形1在铰接点E处产生最大相对误差99%,在铰接点H和N处达到98%.
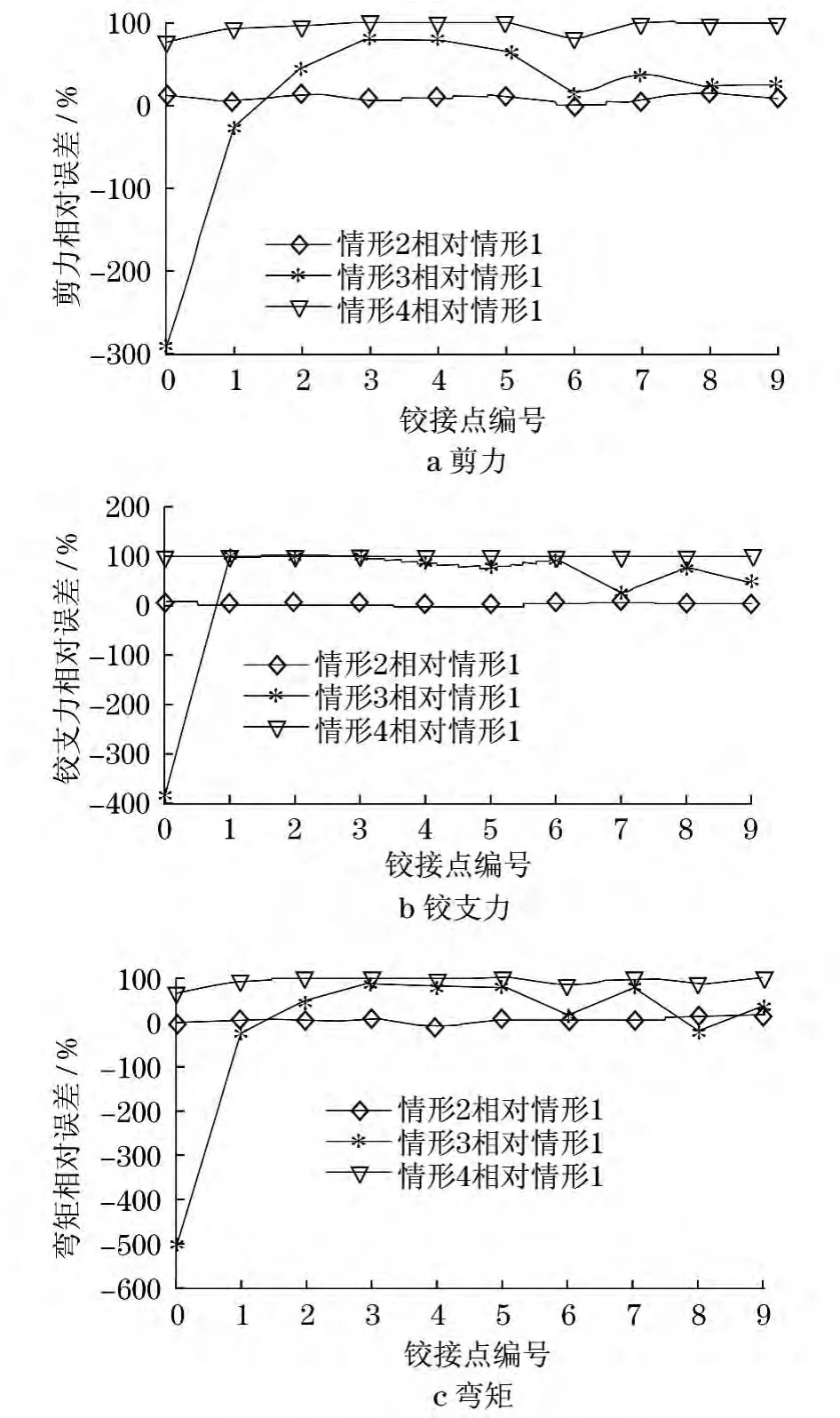
图7 四种情形下的相对误差Fig.7 Relative error under four situations
3.3.2 相对误差原因分析
(1)情形1是采用有限元方法分析,考虑了管力、连杆机构重量、液压油缸重量等所有零部件重量.情形2是利用解析法计算,其管力是通过力的平移转化为平面受力问题,由于混凝土管在臂架上的布置不对称,这种平移处理难免会带来一些误差.但是,从以上分析中可知,无论是剪力、铰支力还是弯矩,情形2相对情形1的相对误差均在10%左右,这是可以接受的,而且这10%的相对误差也不全是情形2的误差,因为利用有限元计算也同样会带来一些问题,如有限元分析是在满足连续性、均匀性、各向同性、线弹性、小变形等前提下进行的,而实际上并非全部满足.
(2)由于管力的影响,情形1中每个节臂的重心偏移至混凝土管所在的那一侧,混凝土管在节臂2段折弯,布置在臂架两边,混凝土管在节臂1至其折弯点上处于一侧,另一折弯点至节臂5上处于另一侧,为了满足臂架的折叠伸展和控制泵车整车高度,节臂3又是折弯的,混凝土管另一折弯点至节臂5段的混凝土管偏心距离又是不相等的,这就使得各节臂的重心不共线.情形3忽略管力,这种简化会使得各节臂之间的重心在一条直线上,情形3相对情形1的相对误差最大达到了388%,这样的误差是不能够接受的.当然最大相对误差388%不能说明误差就果真这么大,由于偏心的存在,力的方向也会发生改变,合力的大小和方向都会随之改变.
(3)情形4将各节臂重量视为集中载荷作用其中点,忽略管力和油缸、连杆等构件的重量.显然,这种简化值得商榷.
4 结论
(1)将混凝土泵车臂架视为均布载荷,且考虑管力,给出了混凝土泵车臂架结构的数学模型以及各铰接点的弯矩、扭矩和铰支力的一般计算公式.
(2)分别利用有限元方法和解析方法求解四种情形下的铰支力、弯矩和剪力,进而得出其相对误差,比较直观地反映了臂架简化带来的影响.
(3)针对臂架结构和实际工况,利用有限元分析软件和解析计算相互验证,说明所建数学模型的合理性,并方便实现计算机编程求解.
[1]尹人奇.48 m混凝土泵车总体设计[J].产品与设计,2006(1):87-90.
YIN Renqi.Overall designing for truck-mounted concrete pump with 48 m boom bracket[J].Product & Technology,2006(1):87-90.
[2]OHMURA T.Truck mounted concrete pump with 27 m long boom[J].IHIEngineering Review,1985,3(18):147 -149.
[3]孙武和.混凝土泵车臂架结构有限元分析及参数计算程序应用[D].长春:吉林大学,2009.
SUN Wuhe.Research on the finite element analysis and parameter computation program of the boom system for the truck-mounted concrete pump[D].Changchun:Jilin University,2009.
[4]唐睿智.混凝土泵车臂架结构分析与优化设计[D].长沙:长沙理工大学,2012.
TANG Ruizhi.Research on the structure and optimal design of the boom system of the truck-mounted concrete pump[D].Changsha:Changsha University of Science & Technology,2012.
[5]张艳伟,佟力,孙国正.基于ANSYS的混凝土泵车臂架结构分析研究[J].武汉理工大学学报:交通科学与工程版,2004,28(4):537-538.
ZHANG Yanwei,TONG Li,SUNGuozheng.A structure analysisof concrete pump’s boom based on ANSYS[J].Journal of Wuhan University of Technology:Transportation Science & Engineering,2004,28(4):537 -538.
[6]仇文宁.混凝土泵车布料杆的位置控制[D].长春:吉林大学,2009.
QIUWenning.Control on the boom’s position of concrete pump truck[D].Changchun:Jilin University,2009.
[7]郭岗,许辉.混凝土泵车臂架结构的几何非线性计算[J].建筑机械,2007(3):69-71.
GUO Gang,XU Hui.Geometrical non-linear calculation for moom structure of truck concrete pump[J].Construction Machinery,2007(3):69-71.
[8]刘鸿文.材料力学[M].4版.北京:高等教育出版社,2004.
LIU Hongwen.Mechanics ofmaterials[M].4th ed.Beijing:Higher Education Press,2004.
