基于改进粒子群算法的管片拼装机齿轮优化

张冠宇，何恩光，赵海峰，刘春光

(1.吉林大学机械科学与工程学院，吉林长春 130022;2.北方重工集团有限公司全断面掘进机国家重点实验室，辽宁沈阳 110141)

随着工程机械的发展，内啮合齿轮由于其中心距小、齿轮传动磨损相对较轻及使用寿命较长等优点［1－2］，被欧洲、日本等广泛应用于管片拼装机回转驱动中，但其存在安装内齿轮的支撑比较困难、外齿轮常是悬臂结构故刚性较差等缺点.

本文基于管片拼装机回转装置工作要求，针对内啮合齿轮传动的缺点，运用在全局搜索性方面进行过改进的粒子群算法［3］对其进行优化，合理设计回转内啮合齿轮传动.

1 内齿轮传动优化设计的数学模型

根据管片拼装机回转驱动机理，基于内啮合齿轮加工和传动中的干涉，以大小齿轮滑动率之差最小作为目标函数，优化内啮合齿轮传动，合理设计回转装置内啮合齿轮传动［4－5］.本文所用符号的物理意义见表1.

1.1 确定设计变量

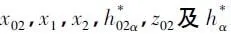
其中，

1.2 目标函数

由于内啮合齿轮传动的限制条件满足与否取决于齿轮和齿刀的有关参数，要做到空间合理的齿轮传动设计需要大量的刀具库信息，这就限制了对于诸如齿轮副体积最小、中心距最大等为设计目标的内齿传动动态设计过程.本文在解决这个问题时，参考齿轮设计初步计算公式确定了负载T1=2.6 kN，最小模数mmin=4.但此时齿数很大，参考GB3811—83所规定的起重机械首先根据类似重型机械(如轮式装载机、起重机等)的设计经验和考虑安全系数，取模数最大值mmax=16.在模数的选取问题上，根据已确立的内齿轮传动限制曲线方程与模数的关系，模数越大会使得变位系数的区域增大.然后根据空间布置要求，近似地取定设计空间接近外围区域的直径，使之为大齿轮的分度圆直径，预估齿数为z1，通过传动比可得到齿数z2.通过对中心距公式的分析，齿数z1和z2确定的前提下，选定加工刀具的参数.结合工作齿轮传动的承载能力，通过分析齿轮传动的失效原因及破坏方式和大模数齿轮相对最大滑动率值比较大的特点，选定使齿根处的最大滑动率接近或相等为设计目标.在相同的工作时间内，大小齿轮参与啮合的次数是不同的，大齿轮的齿廓参与啮合的次数仅为小齿轮的1/u，又由于是两个小齿轮，所以内齿轮齿廓的磨损系数为2/u，即变位系数优化选择时的目标函数为

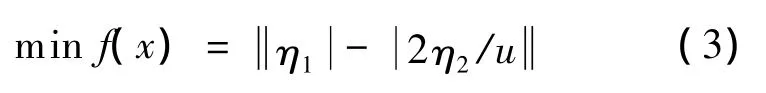
其中，

1.3 设定约束条件

(1)强度约束

根据《机械设计手册》中齿轮设计要求，齿轮应满足接触疲劳强度、弯曲疲劳强度的设计要求，如下所示:

式中:σH为计算接触应力，N·mm－2;σHP为许用接触应力，N·mm－2;σF为计算齿根应力，N·mm－2;σFP为许用齿根应力，N·mm－2.

(2)重合度条件

为了保证直齿齿轮传动的平稳性，要求重合度εγ必须大于 1，一般多要求 εγ≥1.2.

(3)齿廓干涉限制方程

其中，

(4)内齿轮过渡曲线干涉限制条件

(5)外齿轮根部过渡曲线限制条件

(6)内齿轮齿顶厚系数限制条件

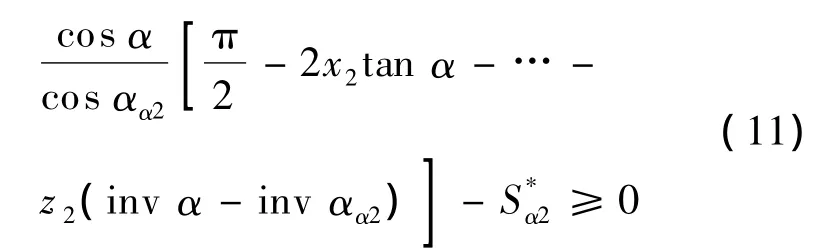
(7)加工内齿轮顶切范成限制条件

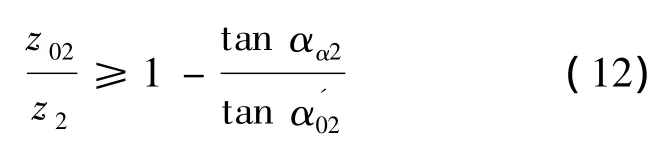
(8)内齿轮的刀根过渡曲线顶切限制条件

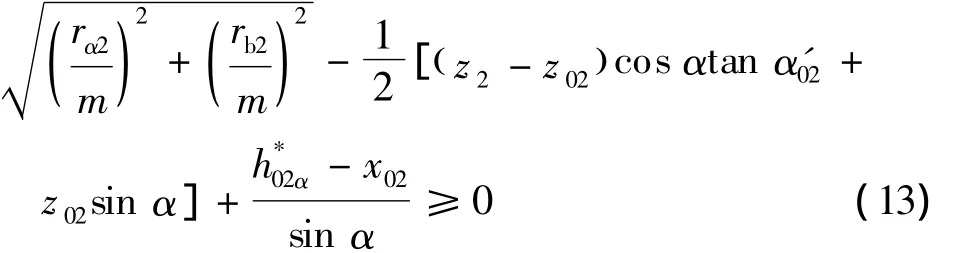
(9)内齿轮径向切入顶切限制条件

内齿轮的刀根过渡曲线顶切是由于在切削过程中，插齿刀的齿根过渡曲线与内齿轮的齿顶发生重叠干涉，致使内齿轮齿顶被切去一部分.这里可查阅《齿轮手册》对应的z0和x0的φ2min，可以避免此干涉.

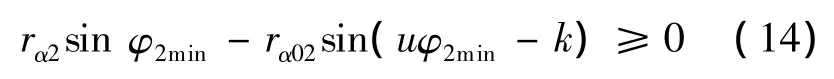
(10)对顶干涉的限制条件

对顶干涉主要是指在少齿差传动中，外齿轮和内齿轮在沿连心线方向上对顶处发生了齿顶的重叠干涉，无法使齿轮副正确安装.

(11)内齿轮顶部有渐开线的限制条件

内齿轮当齿数较少时，有可能齿顶圆直径小于基圆直径.

(12)实际中心距限制条件

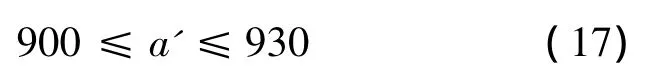
2 改进的粒子群算法

2.1 标准的粒子群算法

假设一个由M个粒子组成的群体在D维的搜索空间以一定的速度飞行，粒子i在t时刻的状态属性设置如下:

粒子在t+1时刻的位置通过下式更新获得:

式中:R1和R2为均匀分布在(0，1)区间的随机数;C1和C2称为学习因子，通常取2;ω为惯性权重.

2.2 改进的粒子群算法

粒子群算法的主要参数有惯性权重、学习因子等.这些参数使得粒子群算法具有较强的局部搜索能力，能够在局部优化中呈现出很好的优化效果.但是在粒子群算法中，对于参数的适当选择仍很难克服其自身的缺陷，即初期收敛速度较快，后期由于所有粒子都向最优的粒子靠近，从而使整个种群陷入到局部最优的境地.

遗传算法(GA)中含有遗传和变异两种特性，遗传特性能够提升优化效率，变异特性则表现出很好的全局搜索性，而禁忌算法中禁忌区域的设定可提高优化效率.为了改进粒子群算法中的不足和保证优化效率，故将遗传和变异两种特性以及禁忌区域融合入粒子群算法中，其流程图如图1所示.

3 小直径全断面掘进机优化实例

对某小直径全断面掘进机管片拼装机的回转驱动内啮合齿轮传动装置进行优化，已知其初始设计参数如表2所示.

以原始设计值为出发点，利用改进的粒子群算法对此内啮合齿轮传动装置进行优化，经优化后的结果如表3所示.

图1 改进粒子群算法流程图Fig.1 Flowchart of improved particle swarm optim ization algorithm

表2 齿轮的原始设计值Tab.2 Values of initial design parameters for gear

表3 内啮合齿轮优化结果Tab.3 Optim ization results

通过表2和3的对比，可以看出，经优化后的内啮合齿轮的相对滑移率得到了很好的改进.

4 总结

本文以小直径全断面掘进机回转驱动内啮合齿轮传动的工作需求为基础，寻求在小齿轮尽可能小、中心距尽可能大的前提下，建立以内齿轮传动的相对滑动率为目标函数，以内啮合齿轮加工和传动中的干涉为约束条件，利用改进的粒子群算法对回转驱动内啮合齿轮进行优化，从而提高内啮合齿轮的啮合质量.

［1］张展，朱景梓，秦立高.渐开线内啮合圆柱齿轮传动［M］.北京:国防工业出版社，1991.

ZHANG Zhan，ZHU Jingzi，QIN Ligao.Internal meshing involute cylindrical gear transmission［M］.Beijing:National Defence Industry Press，1991.

［2］齿轮手册编委会.齿轮手册［M］.北京:机械工业出版社，2000.

Manual Gear Editorial Board.Gear manual［M］.Beijing:China Machine Press，2000.

［3］FAN S-K S，LIANG Y-C，ERWIE Z.A genetic algorithm and a particle swarm optimizer hybridized with Nelder-Mead simplex search［J］.Computers ＆ Industrial Engineering，2006，50(4):401－425.

［4］胡国明，姜从盛，万卉.开式重载齿轮变位系数的优化［J］.水泥技术，1998(1):20－22.

HU Guoming，JIANG Congsheng，WAN Hui.Optimization ofmodification coeffofopen-case heavy-duty gears［J］.Cement Technology，1998(1):20 －22.

［5］ZHANG Guanyu，WANG Guoqiang，LIXuefei，et al.Global optimization of reliability design for large ballmill gear transmission based on the krigingmodel and genetic algorithm［J］.Mechanism and Machine Theory，2013，69:321 －336.