基于ADAMS的矿用自卸车车架动态应力分析

成 凯，刘维维，廖清德，郑 森，郝庆升

(1.吉林大学机械科学与工程学院，吉林长春 130022;2.厦门厦工重工有限公司，福建 厦门 361000)

矿用自卸车经常工作在露天矿区，由于作业路况恶劣，载重量大等原因导致其零部件很容易发生破坏，其中车架的破坏尤其常见.传统的车架设计仅考虑静态情况，但这已经不能满足现代设计要求，从系统工程和可靠性的分析要求角度，必须对系统动力学进行准确预估.因此，研究车架的动态应力具有十分重要的理论意义和工程实用价值.

车架作为整车主要的承力部件其自身的弹性变形对整车的动态性能影响十分重要，所以有必要把车架处理成实际中可以变形的柔性体.本文利用多体动力学仿真软件ADAMS，将车架柔性化后建立整车刚柔耦合模型，选取矿区典型路面并考虑路面不平度的激励，研究车架的动态应力.

1 系统模型的建立

1.1 车体建模

仿真使用的三维模型是在Pro/E软件中以厂家提供的模型为基础，在进行了必要的简化后，转化成parasolid的x－t格式文件后导入到ADAMS/VIEW模块中.修改质量与转动惯量，按实际情况添加约束关系，整车三维模型如图1所示.

将车架模型作为一个刚性载体，这个假设只适用于明显低于车架第一阶弯曲固有频率的频率范围，如果想让模型在高于这个频率时仍然适用，在简化模型时必须考虑车架的弹性.另外车架作为主要承力部件，其变形会引起其他零件的干涉等影响.

图1 某矿用自卸车整车三维动力学模型Fig.1 Three-dimensional dynam icmodel ofm ining dum per truck

本文是在Hypermesh中对车架模型进行网格划分，将网格导入ANSYS中添加刚性区域后生成MNF中性文件.由于车架与转向系统、悬架系统、驾驶室悬置系统等部件的连接点都在车架外部，为了模拟实际连接情况，提高仿真精度，需要在相应的连接区域创建刚性区域，车架与其他零件之间通过刚性区域传递力.本文共建立了19个外部连接接点.车架的有限元网格与刚性区域如图2所示.

图2 外部连接点及刚性区域示意图Fig.2 External connection points and rigid areas

ADAMS是采用模态叠加法对弹性体求解，其基本假设是柔性体相对于连体坐标系做小的线性变形运动，而连体坐标系同时也在做大的非线性运动.弹性体运动的拉格朗日方程如下［1］:

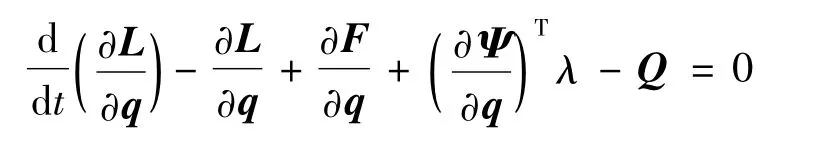
式中:L为拉格朗日算子，定义为动能与势能的差值;F为能量耗散函数;Ψ为约束方程;λ为相对于约束的拉格朗日乘数;q为总体坐标;Q为总体作用力.代入质量、重力、刚度和阻尼矩阵得到运动方程的最后形式如下:

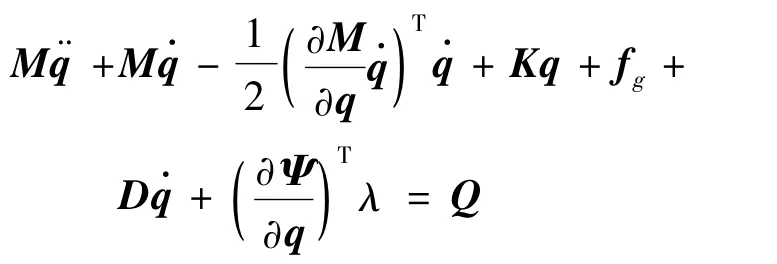
式中:M为质量矩阵，K为刚度矩阵，fg为由重力产生的作用力，D为阻尼矩阵.

1.2 路面建模

本文对车辆-道路的相互作用作如下基本假设［2］:

(1)由于道路表面位移响应的尺度相对于车辆轮胎和悬架变形的尺度来说非常小，在车辆数字仿真时可假设道路本身是刚性的，没有变形的，据此计算车辆在固定道路不平度时输入的响应.

(2)只有车辆对道路累积长期作用才会引起道路表面不平度的变化，道路不平度不随车辆的短期经过而变化.据此，在计算短期内由于车辆的经过对道路造成的作用力时，不考虑车辆对道路破坏造成的道路不平度变化，按固定的道路不平度输入计算车辆响应.

基于以上假设，根据矿区的实际情况确定路面等级为D级路面，选取典型的恶劣路面利用Pro/E软件建立三维模型后导入Hypermesh中进行网格划分，输出节点和单元信息，再在Matlab中编制路面谱程序生成D级路面的路面不平度.本文采用正弦叠加原理进行随机路面激励构造，其基本思想是根据如下路面不平度功率谱密度表达式［3］:

式中:n0为参考空间频率，一般取为0.1 m－1;w为路面功率谱密度频率结构的频率指数，一般取2;n为空间频率;q为路面相对于基准平面的高度.

在空间频率nmin＜n＜nmax内的路面不平度功率谱密度Gq(n)，利用平稳随机过程的频谱展开性质，路面不平度方差

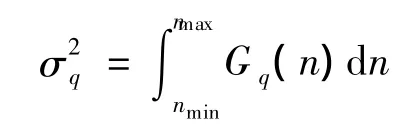
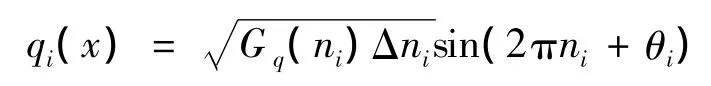
如果路面的纵向为x，横向为y，则三维空间中路面的不平度可表示为

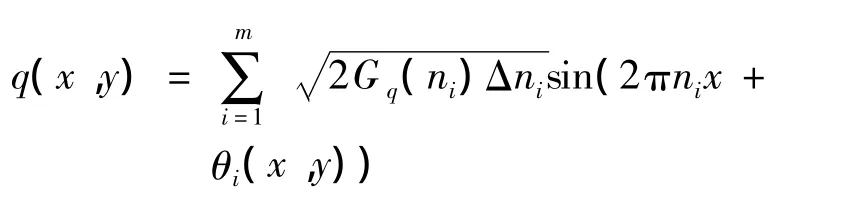
式中:θi(x，y)为在路面上任意点(x，y)处属于［0，2π］间的随机数.

本文取空间频率范围0.001 m－1＜n＜10 m－1，生成的D级路面不平度数据如图3和4所示.从图4可见，相应的功率谱密度模拟值与解析值相吻合.

最后根据节点单元和路面不平度信息编制成路面谱文件，生成如图5所示的典型矿区路面.

2 仿真分析

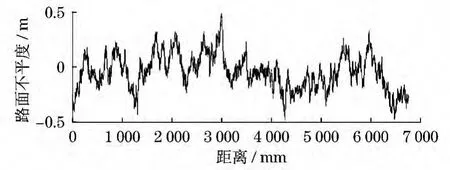
图3 D级路面不平度Fig.3 Road roughness of D-class

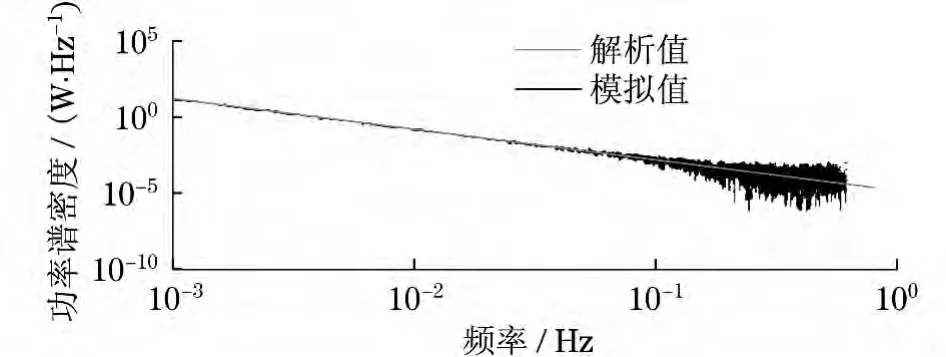
图4 D级路面功率谱密度Fig.4 Comparison of power spectral density between standard road spectrum and restructured road spectrum

图5 典型矿区路面示意图Fig.5 Typicalm ine road surface

将上文所生成的路面文件导入动力学模型中进行仿真，如图6所示.为了提高仿真精度，采用去掉前6阶刚体模态的前40阶固定边界的正交模态.矿用自卸车载货50 t，以5 km·h－1的速度匀速过渡到凹凸路面.路面条件为水平路面凸台高为150 mm，凹坑深度为150 mm，长度均为5 000 mm.

图6 整车刚柔耦合动力学模型Fig.6 Rigid-flexible coupling dynamical model

2.1 左前轮和右中后轮沉陷同时右前轮和左中后轮越障(工况1)

当车左前轮和右中后轮沉陷同时右前轮和左中后轮越障时，从图7和8可以看出，此时危险点在第2根横梁附近的左侧纵梁上下表面.去掉前5 s车因自重下降引起的振动，截取5～70 s的动态应力曲线.图9为在此工况下车架应力最大点处动态应力曲线.

图7 车架上表面大应力区域示意图(工况1)Fig.7 Big stress areas on upper surface of frame (working condition 1)

图8 车架下表面大应力区域示意图(工况1)Fig.8 Big stress areas on lower surface of frame (working condition 1)

图9 车架上下表面应力最大点动态应力曲线(工况1)Fig.9 Dynamic stress curve of big stress areas on upper and lower surface of frame(working condition 1)

自卸车在21 s左右进入左前轮和右中后轮沉陷同时右前轮和左中后轮越障状态.从图9可以看出，此时车架上表面的动态应力最大值为90 MPa，下表面的动态应力最大值为85 MPa，车架主要受垂向弯曲和扭转作用.

此外，在20 s和35 s处的峰值出现波动，这主要是因为车左前轮和右中后轮沉陷的同时右前轮和左中后轮越障，使得左侧后板簧达到最大行程，从而后板簧的前后座先后与限位块相碰，导致车架承受更严重的偏载冲击，产生应力波动.

2.2 前轮越障同时中后轮沉陷(工况2)

当车前轮越障中后轮沉陷时，从图10和11可以看出，此时危险点在第4根横梁盖板左右两侧纵梁的上下表面.图12为车架应力最大点处动态应力曲线.

图10 车架上表面大应力区域示意图(工况2)Fig.10 Big stress areas on upper surface of frame (working condition 2)

图11 车架下表面大应力区域示意图(工况2)Fig.11 Big stress areas on lower surface of frame(working condition 2)

自卸车在48 s左右进入前轮越障同时中后轮沉陷状态.从图12可以看出，此时车架上表面的动态应力最大值为70 MPa，下表面的动态应力最大值为50 MPa，车架主要受垂向弯曲作用.

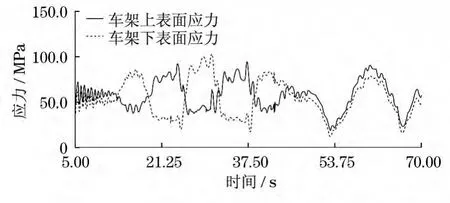
图12 车架上下表面应力最大点动态应力曲线(工况2)Fig.12 Dynam ic stress curve of big stress areas on upper and lower surface of frame(working condition 2)

2.3 前轮沉陷同时中后轮越障(工况3)

当车前轮沉陷中后轮越障时，从图13和14可以看出，此时危险点在第2根横梁与第3根横梁中间的两侧纵梁上下表面.图15为车架应力最大点处动态应力曲线.

自卸车在56 s左右进入前轮沉陷同时中后轮越障状态.从图15可以看出，此时车架上表面的动态应力最大值为75 MPa，下表面的动态应力最大值为100 MPa.车架主要受垂向弯曲作用，应力随着路面起伏而波动.

图13 车架上表面大应力区域示意图(工况3)Fig.13 Big stress areas on upper surface of frame(working condition 3)

图14 车架下表面大应力区域示意图(工况3)Fig.14 Big stress areas on lower surface of frame(working condition 3)

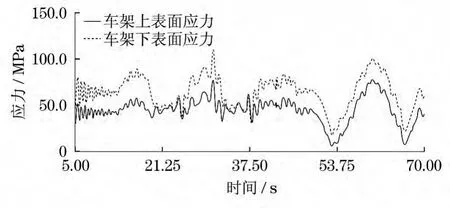
图15 车架上下表面应力最大点动态应力曲线(工况3)Fig.15 Dynam ic stress curve of big stress areas on upper and lower surface of frame(working condition 3)

3 结论

(1)车架的弹性变形对整车动态性能的影响不可忽视，所以把车架处理成柔性体进行整车的刚柔耦合动力学仿真具有一定的可信度和合理性.

(2)车架第2根横梁两侧的纵梁上下表面的动态应力较大，这是因为两侧纵梁直接受车箱和物料的重力作用.车架第3、第4根横梁盖板边缘处的应力也较大，这主要是由应力集中引起的，建议在焊接时要保证焊接工艺，盖板的边缘尽量圆滑过渡，尽量避免铸造时出现缩松、缩孔或夹层.另外第2根横梁两侧立板的开孔处也存在应力集中，应该注意车架工艺孔和减重孔的开孔位置，尽量避免截面和载荷的双重突变.

(3)路面情况对车架的动态应力影响很大，车辆在搓板路面上行驶时车架受到交变应力的作用，虽然工作应力低于车架材料的强度极限，但在经历一定的工作时间之后可能引起疲劳失效，造成车架的疲劳断裂.

(4)钢板弹簧刚度对车架动态应力影响复杂，如果提高钢板弹簧刚度会降低整车的平顺性，而降低钢板弹簧刚度则会使车架产生更大的动应力.另外，由于限位块的作用使得钢板弹簧的行程受到很大的限制，行驶在沉陷或越障等路面上时，由于轮胎的着地力非常不均匀，使得车架承受更严重的偏载冲击载荷，从而产生更大的动态应力.

［1］刑俊文.MSC.ADAMS/Flex与AutoFlex培训教程［M］.北京:科学出版社，2006.

XING Junwen.Train course of MSC.ADAMS/Flex and AutoFlex［M］.Beijing:Science Press，2006.

［2］任卫群.车-路系统动力学中的虚拟样机［M］.北京:电子工业出版社，2005.

REN Weiqun.Vitrual prototype of vehicle-road system dynamics［M］.Beijing:Electronic Industry Press，2005.

［3］郝赫.多轴重型汽车刚弹耦合虚拟样机分析与匹配［D］.长春:吉林大学，2011.

HAO He.Analysis and matching on rigid-flexible coupling virtual prototype of heavy-duty truck with multi-axles［D］.Changchun:Jilin University，2011.