细长轴车削加工让刀量误差优化

邓志平，张 洪，金 龙，龙 俊，张正义

(西华大学机械工程与自动化学院，四川成都 610039)

在机械加工中，通常将长度与直径之比大于20的轴，定义为细长轴.细长轴应用极其广泛且需求量大，是制造业中不可缺少的一类重要零件.但在制造加工中，受机床几何误差、热误差、切削力误差以及细长轴自身刚度不足、振动等因素影响，很难保证加工精度［1］.

为进一步提高细长轴加工精度，国内外学者进行了数控内部参数修正补偿方面的研究［2－4］.这些研究在一定程度上能够提高细长轴加工精度，但由于数控内部参数修正补偿属于静态补偿且修正参数是在特定的环境下测量出来的，在其他环境下应用就会产生误差.基于此不足，本文推导出了一个有关细长轴切削参数、材质、长度以及直径的让刀量公式，并对该公式进行了优化处理.

1 建立径向力作用下的弯曲模型

细长轴加工一般采用一夹一顶装夹方式，将卡盘端A简化为固定端，顶尖端B简化为铰链支座，建立受力分析模型［5－8］，如图1 所示.

图1中，FA和FB分别表示A和B两点处的支座反力，F表示径向力，MA表示A点处的弯矩，a表示径向力F到A点的位移，b表示径向力F到B点的位移，l表示工件长度，x表示截面C到A点的位移.

根据图1，建立平衡公式

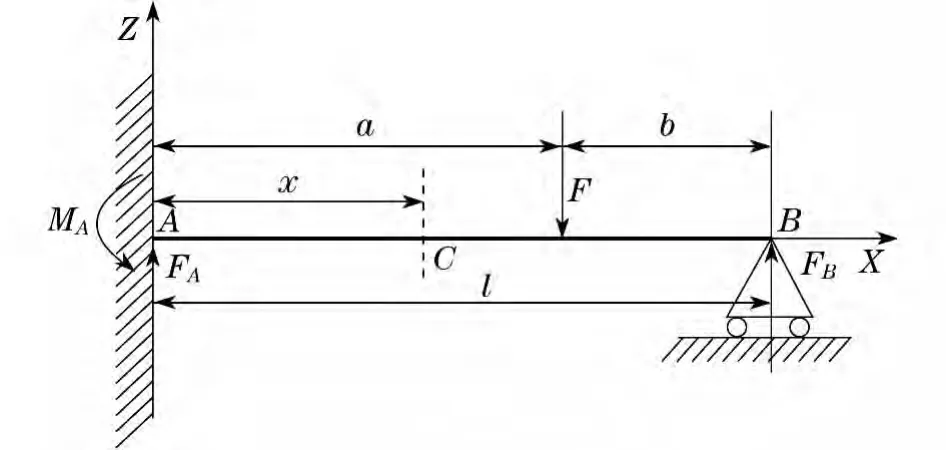
图1 细长轴受力分析模型Fig.1 Force analysis of slender shaftmodel

该力学模型属于一次超静定梁问题，因而需增加一形变协调公式.选B点为参考点，可得

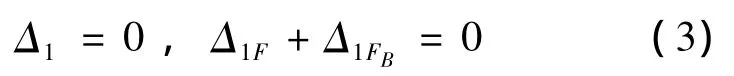
式中:Δ1表示B端沿FB方向的位移，Δ1F表示力F单独作用下引起的位移，Δ1FB表示力FB单独作用下引起的位移.

由基本静定系和线弹性原理可知，Δ1FB=δFB，δ表示B点沿FB方向因这一单位力引起的位移，利用莫尔积分法得

代人式(3)得

再代人式(1)和(2)得

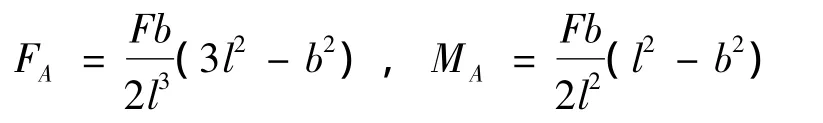
由材料力学可知，AC段上的弯矩

转角公式为

即

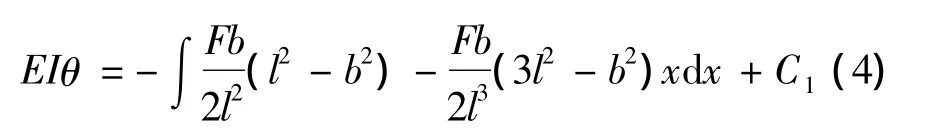
挠度公式为

即

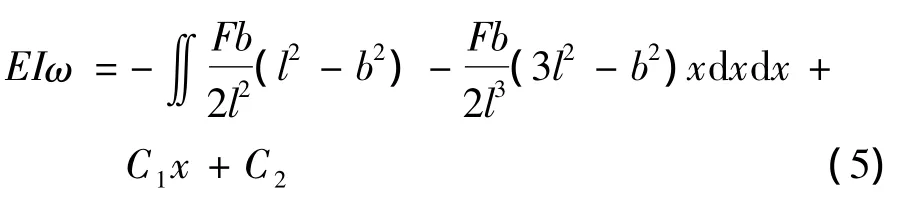
式(4)和(5)中 θ表示转角，C1和C2表示积分常数，ω表示挠度，EI表示弯曲刚度.由于A点为固定端，其挠度和转角都为0，即x=0 时，ω =0，θ=0，所以C1=0，C2=0.

令x=a，则b=l－x，代人式(4)和(5)，得C点的挠度公式为

即为该点理论让刀量公式.

2 理论让刀量公式的仿真验证与优化

在进行ANSYS静力学分析前，考虑到细长轴实际加工过程中，受各种不利因素影响且相互之间关系复杂，为方便本次仿真研究，对一些因素进行了特殊处理并作如下假设:① 假设刀具在仿真中不产生任何磨损或变形;② 假设刀具径向力F始终保持恒定不变.

细长轴的车削模型是以梁理论为基础建立的简支梁模型［9］，此次模拟仿真选用基于Timoshenko梁理论建立的Beam188单元.细长轴模拟仿真参数为l=1 000 mm，直径d=50mm，密度 ρ=7.8 g·cm－3，泊松比0.3，弹性模量E=2.1 ×1011Pa，背吃刀量 2 mm，径向力F=132 N(试验测得).在进行细长轴的网格划分时，一般来说，网格划分越细，仿真结果越准确.但考虑到试验数据的处理和计算，选择在X方向上把细长轴离散划分为100份，共10组，每一组长度为10 cm，1号节点为卡盘端A，101号节点为顶尖端B.图2为细长轴进行网格划分完后的有限元模型，图3为细长轴节点编号示意图.

图2 细长轴有限元模型Fig.2 Finite elementmodel of slender shaft

在进行加载时，载荷设置为分步载荷，每一步载荷加载位置间相距为10个节点.对1号节点施加全约束，对101号节点施加沿Y和Z方向的位移约束.本次仿真采用正向车削(刀具位于2号节点处，细长轴的上方水平向左走刀).图4为加载载荷F在45号节点处细长轴弯曲变形图.

图3 细长轴静态仿真节点编号示意图Fig.3 Diagram of node number for slender shaft static simulation

图4 45号节点处细长轴弯曲变形图Fig.4 Bending deformation of slender shaft at No.45 node

为了准确反映出细长轴在车削加工中的整体变形情况，可通过后处理模块，利用节点位移查看命令，显示出刀具在指定节点处Z方向上的位移值，此位移值即为刀具加工点的让刀量.本文仿真试验统计了12个不连续节点处的位移值，如图5所示.

图5 节点位移值Fig.5 Node displacement value

将l=1 000 mm，d=50 mm，F=132 N，E=2.1×1011Pa，I=πd4/64 代入式(6)，计算出刀具加工点的理论让刀量公式为

利用Matlab软件［10］对式(7)求解，考虑实际加工中造成让刀量误差的因素众多，故在该理论让刀量公式中引入了修正系数m，得到刀具加工点的让刀量精确预测公式如下:

为保证式(8)的准确性和可行性，分别绘制出了修正参数m=0.9，1.1，1.3 时的位移 － 让刀量曲线，如图6所示.

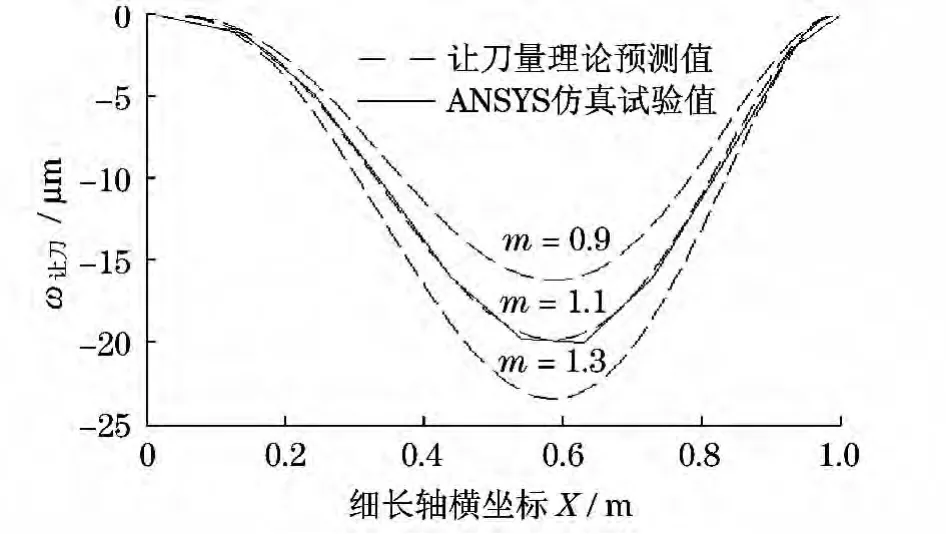
图6 位移－让刀量曲线Fig.6 Displacement-relieving amount curve

图6分析可知，刀具加工点的理论让刀量曲线和ANSYS仿真曲线走势大致相同，从而验证了刀具加工点的理论让刀量公式的准确性.当径向力修正系数m=1.1时，理论预测值和仿真值基本一致，因此确定m取1.1，从而为数控刀具补偿提供了运动轨迹曲线.

3 结论

本文对ANSYS静力学仿真所得的刀具让刀量曲线和理论让刀量曲线进行对比分析，并通过Matlab对理论让刀量曲线进行了优化.结果表明，经过优化后的让刀量曲线和仿真所得让刀量曲线具有较好的一致性，为数控车削加工提供更加精确的补偿曲线.

［1］刘小艳.细长轴的车削加工工艺［J］.装备制造技术，2013(1):59－60.

LIU Xiaoyan.Tin and long shaft turningmachining process［J］.Equipment Manufacturing Technology，2013(1):59 －60.

［2］李玉玲，李志峰，魏伟锋.车削加工细长轴的理论误差分析［J］.煤矿机械，2008，29(10):108 －109.

LI Yuling，LI Zhifeng，WEIWeifeng.Theoretic error analysis in turning of slender shaft［J］.Coal Mine Machinery，2008，29(10):108－109.

［3］王小翠，李蔚，侯志敏.细长轴车削用量优化与加工变形误差补偿技术的研究［J］.制造技术与机床，2007(10):85－88.

WANG Xiaocui，LIWei，HOU Zhimin.Research on cutting parameters optimization and error compensation in slender bar turning［J］.Manufacturing Technology ＆ Machine Tool，2007(10):85－88.

［4］刘田龙.用进刀量补偿法减少细长轴车削加工误差［J］.电子设计工程，2012，20(21):100 －102.

LIU Tianlong.Amount of feed compensation method for reducing thinmajor axis turning error［J］.Electronic Design Engineering，2012，20(21):100 －102.

［5］胡月来.细长轴加工的误差补偿［J］.华中农业大学学报，2005，24(3):312 －314.

HU Yuelai.Machining error correction of slender shaft［J］.Journal of Huazhong Agricultural University， 2005，24(3):312－314.

［6］吴能章.轴类零件加工的鼓形误差预报与补偿［J］.西华大学学报:自然科学版，2005，24(1):30 －33.

WU Nengzhang.Prediction and compensation for drum-shaped error in themachiningof shaft-type parts［J］.Journal of Xihua University:Natural Science，2005，24(1):30 －33.

［7］许鹏，邓志平.细长轴加工的单片机误差补偿系统设计［J］.机床与液压，2011，39(22):91 －92.

XU Peng，DENG Zhiping.Design of error compensation system for machining of slender shaftbased on SCM［J］.Machining Tool＆ Hydraulics，2011，39(22):91 －92.

［8］罗迎社，李卓球.材料力学［M］.武汉:武汉理工大学出版社，2001.

LUO Yingshe，LI Zhuoqiu.Mechanics ofmaterials［M］.Wuhan:Wuhan University of Technology Press，2001.

［9］邓凡平.ANSYS 10.0有限元分析自学手册［M］.北京:人民邮电出版社，2007.

DENG Fanping.ANSYS10.0 finite elementanalysis of self-study handbook［M］.Beijing:Posts ＆ Telecom Press ，2007.

［10］郭仁生.机械工程设计分析和MATLAB应用［M］.北京:机械工业出版社，2011.

GUO Rensheng.Mechanical engineering design of analysis and MATLAB application［M］.Beijing:China Machine Press，2011.