非奇异H-矩阵新的含参数细分迭代判别法
2014-07-24肖丽霞张俊丽
肖丽霞,张俊丽
(内蒙古民族大学数学学院,内蒙古 通辽 028043)
非奇异H-矩阵新的含参数细分迭代判别法
肖丽霞,张俊丽
(内蒙古民族大学数学学院,内蒙古 通辽 028043)
结合矩阵自身的元素,构造了含参数的迭代公式,进而细分了矩阵非对角占优行指标集.利用广义严格α-对角占优矩阵与非奇异H-矩阵的关系,给出了非奇异H-矩阵一组新的细分迭代判定准则,推广和改进了已有的结果,通过数值算例说明了结果的优越性.
非奇异H-矩阵;α-对角占优矩阵;不可约;非零元素链
1 引言与符号
非奇异H-矩阵是一类应用广泛的特殊矩阵,在计算数学、矩阵理论、控制论等领域发挥着重要作用.对非奇异H-矩阵判定方法的研究,近年来引起许多数学工作者的关注,并取得了一系列的研究成果[19].本文给出了一类新的含参数细分迭代判别法,对文献[1-5]的结果进行了推广和改进.
为叙述方便,引进下列记号和定义,设A=(aij)∈Cn×n为n阶复方阵,N≜{1,2,···,n}, α∈[0,1].记

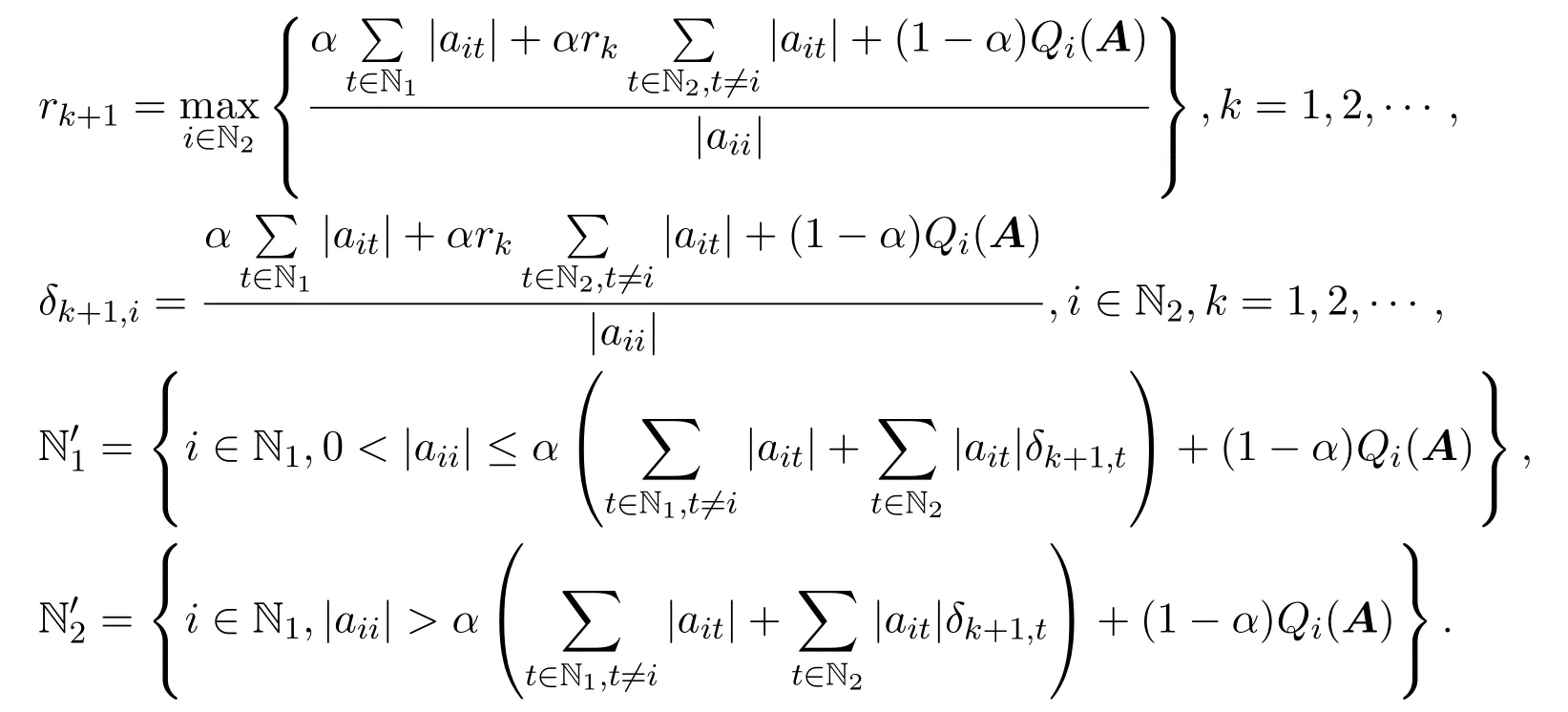
显然有δk+1,i≤rk+1≤rk≤r1<1(∀k∈Z+,i∈N2).
定义 1.1[6]设A=(aij)∈Cn×n,若|aii|≥(>)Ri(A)(∀i∈N),则称A为(严格)对角占优矩阵,记为A∈D0(A∈D);若存在正对角矩阵X使得AX∈D,则称A为广义严格对角占优矩阵,记为A∈D∗.
定义 1.2[6]设A=(aij)∈Cn×n,若存在α∈[0,1],使得
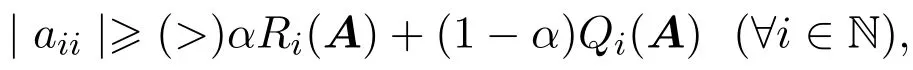
则称A为α-(严格)对角占优矩阵,记为A∈D0(α)(A∈D(α));若存在正对角矩阵X 使得AX∈D(α),则称A为广义严格α-对角占优矩阵,记为A∈D∗(α).
2 主要结果
引理 2.1 [7]设A=(aij)∈Cn×n,若A∈D(α),则A∈D∗.
引理2.2 [8]设A=(aij)∈Cn×n,若存在正对角矩阵X,使AX∈D∗,则A∈D∗.
定理 2.1设A=(aij)∈Cn×n,且N′1,N′2/=∅,若存在k∈Z+(∀i∈N′1,∀j∈N′2),满足:
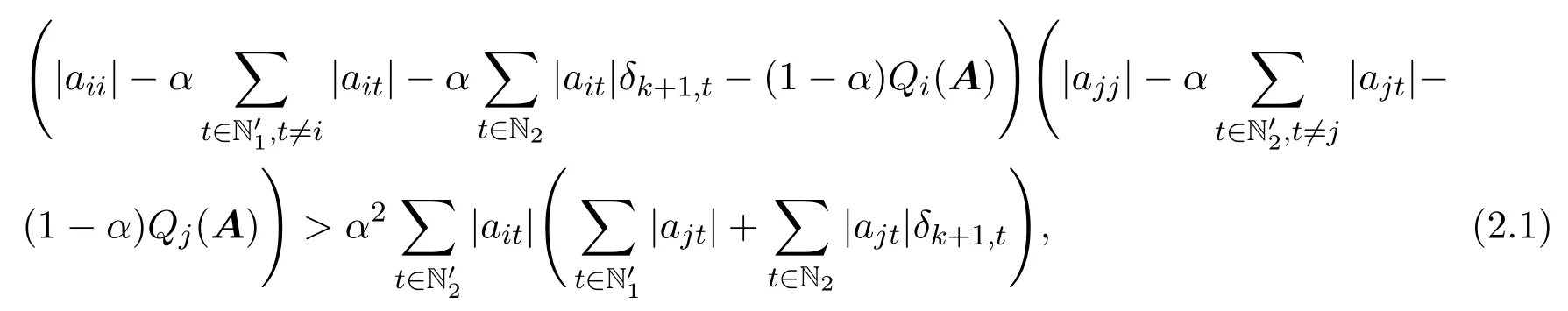
则A为非奇异H-矩阵.
证明令
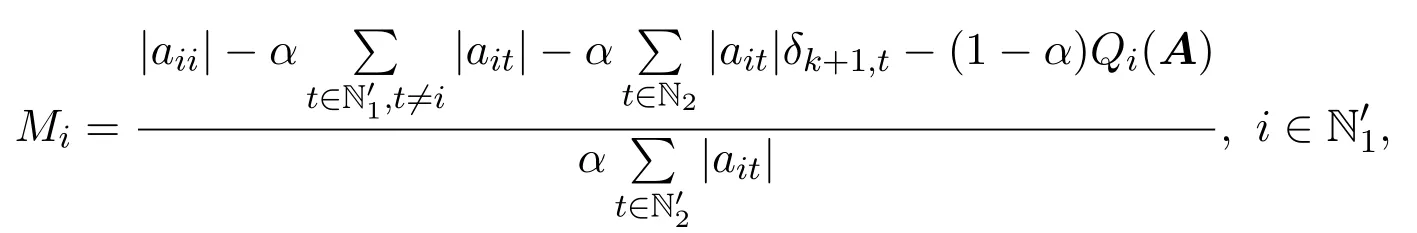

因为0 取正对角矩阵X1=diag(d1,d2,···,dn),并记B=AX1,其中 3) ∀i∈N2,可得 综上所述,有|bii|>αRi(B)+(1−α)Qi(B)(∀i∈N)成立,则B∈D(α),由引理2.1知B=AX1∈D∗,其中X1为正对角矩阵,根据引理2.2,则A∈D∗,因此矩阵A为非奇异H-矩阵. 引理 2.3 [7]设A=(aij)∈Cn×n,若A∈D0(α),A不可约,且N2/=∅,则A∈D∗. 定理 2.2设A=(aij)∈Cn×n,且A不可约,若存在满足: 且至少有一严格不等式成立,则A为非奇异H-矩阵. 证明如同定理2.1的证明,记Mi,mj,则因为0 取正对角矩阵X2=diag(d1,d2,···,dn),并记B=AX2,其中 类似于定理2.1的证明过程,可得|bii|≥αRi(B)+(1−α)Qi(B)(∀i∈N),且至少有一个严格不等式成立.由A不可约,可得B不可约,则B为不可约α-对角占优矩阵,由引理2.3可知B=AX2∈D∗,其中X2为正对角矩阵,根据引理2.1,则A∈D∗,因此矩阵A为非奇异H-矩阵. 记 腾讯董事会主席马化腾凭借328亿美元的身家蝉联榜单第二名,但他的财富缩水了62亿美元。去年的首富、中国恒大董事局主席许家印的排名跌至第三名。许家印的身家为308亿美元,下降28%,折合约117亿美元,他是今年财富值降低最多的富豪。 引理 2.4 [7]设 A=(aij)∈Cn×n,若 A ∈D0(α),并且 ∀i∈N3,都有非零元素链aik1ak1k2...akpj,使得j∈N2,则A∈D∗. 定理 2.3设A=(aij)∈Cn×n,且N′1,N′2/=∅,若存在k∈Z+(∀i∈N′1,∀j∈N′2),满足: 证明如同定理2.2的证明,可得|bii|≥αRi(B)+(1−α)Qi(B)(∀i∈N).其中 成立; 成立,则B为非零元素链对角占优矩阵.根据引理2.4,B=AX2∈D∗,其中X2为正对角矩阵.根据引理2.1,则A∈D∗,因此矩阵A为非奇异H-矩阵. 输入:已知矩阵A,参数α,迭代次数k. 输出:正对角矩阵X. 1)若aii=0(∃i∈N)或N2=∅,输出:矩阵A不是非奇异H-矩阵”,停止;若N1=∅,输出:矩阵A是非奇异H-矩阵”,停止;否则执行2); 2)若N1/=∅且N2/=∅, 成立,则输出“矩阵A是非奇异H-矩阵”,停止;否则输出“不确定矩阵A是否为非奇异H-矩阵”,停止. 例4.1设 取α=0.5,则N1={1,2,3},N2={4,5},令k=1,可得r0=1,r1=0.5,δ2,4=0.45, δ2,5=0.2375,r2=0.45,则取i=3,j=1,则 取i=3,j=2,则 可见矩阵A满足定理2.1的条件,因此矩阵A为非奇异H-矩阵.但 所以矩阵A不能由文献[1]中定理2判定.又因为 所以矩阵A不能由文献[2]中定理1判定.又因为 所以矩阵A不能由文献[3]中定理1判定.又因为 所以矩阵A不能由文献[4]中定理1判定.经验证,对α=0.1,0.2,···,1.0,矩阵A不能由文献[5]中定理1判定. [1]黄廷祝.非奇H矩阵的简捷判据[J].计算数学,1993,15(3):318-328. [2]高中喜,黄廷祝,王广彬.非奇H-矩阵的充分条件[J].数学物理学报:A辑,2005,25(3):409-413. [3]黄泽军,刘建州.非奇异H矩阵的一类新迭代判别法[J].工程数学学报,2008,25(5):939-942. [4]孙德淑.非奇异H-矩阵的判定准则[J].温州大学学报,2009,30(3):18-21. [5]尹如军,徐仲,陆全.非奇H-矩阵的细分迭代判别准则[J].工程数学学报,2013,30(3):433-441. [6]孙玉祥.广义对角占优矩阵的充分条件[J].高等学校计算数学学报,1997,19(3):216-223. [7]Sun Yuxiang.An improvement on a theorem by Ostrowski and its applications[J].Northeastern Math.J., 1991,7(4):497-502. [8]Berman A,Plemmons R J.Nonnegative Matrices in the Mathematical Sciences[M].Philadephia:SIAM Press,1994. [9]韩贵春,钱茜,张俊丽.Ostrowski定理的推广与非奇异 H-矩阵的实用判定 [J].纯粹数学与应用数学, 2013,29(6):601-608. New subdivided and iterative criteria with parameter for nonsingular H-matrices Xiao Lixia,Zhang Junli Associating the elements of the matrix,the iterative formulas with parameter are constructed,and then the index set of non diagonally dominant rows in a square matrix is subdivided.According to the relations between generalized α-diagonally dominant matrices and nonsingular H-matrices,a set of new subdividing and iterative criteria for nonsingular H-matrices is obtained,which extend and improve some related results.A numerical example is used to show the advantages of the results. nonsingular H-matrix,α-diagonally dominant matrix,irreducible,non-zero elements chain O151.21 A 1008-5513(2014)004-0386-07 10.3969/j.issn.1008-5513.2014.04.008 2014-05-25. 内蒙古自治区高等学校科学技术研究项目(NJZY13159). 肖丽霞(1980-),硕士,讲师,研究方向:数值代数. 2010 MSC:15A57
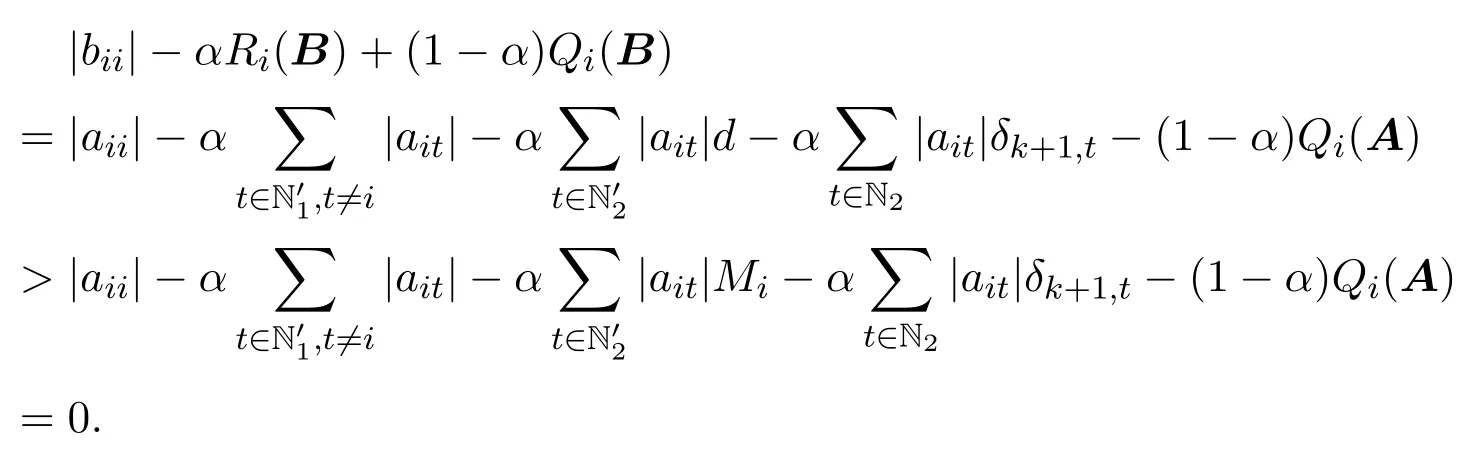
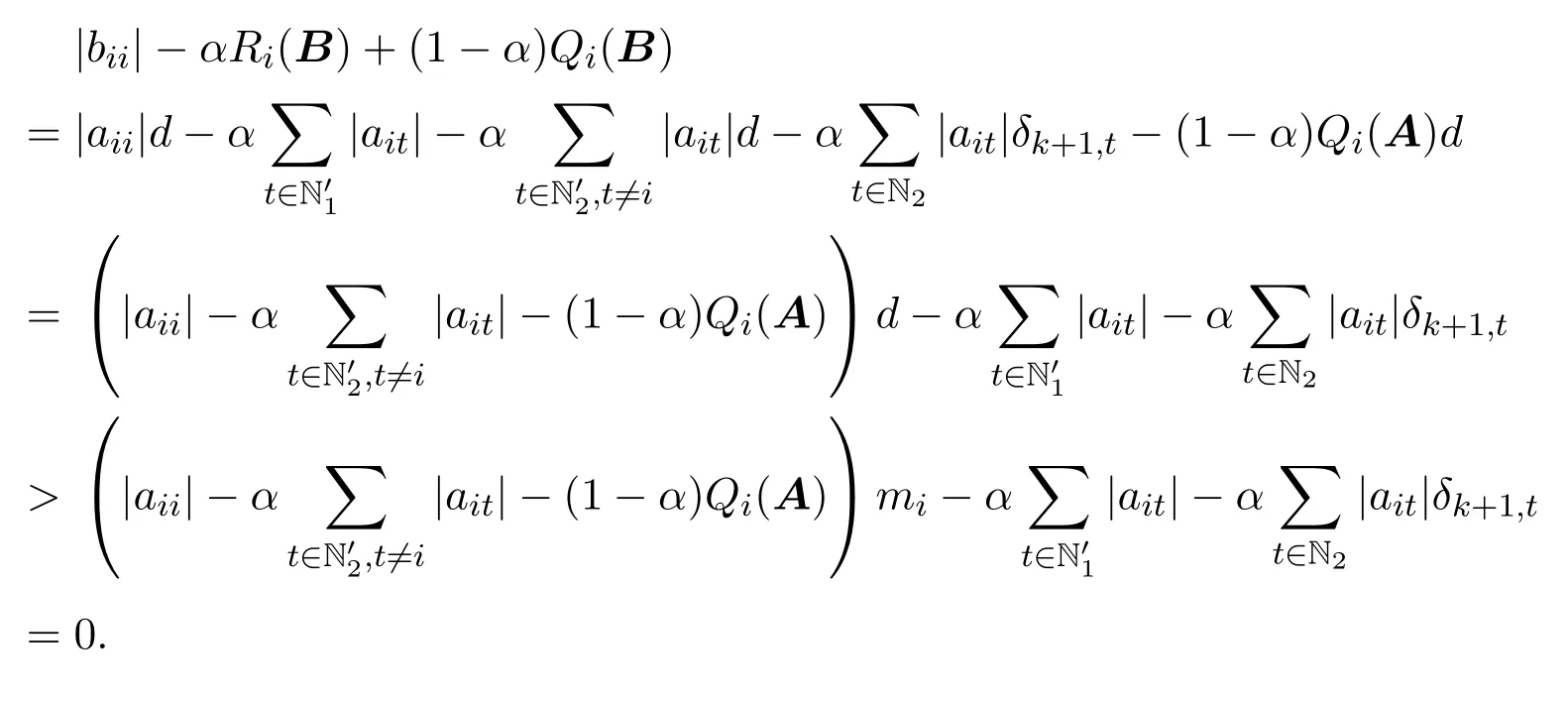
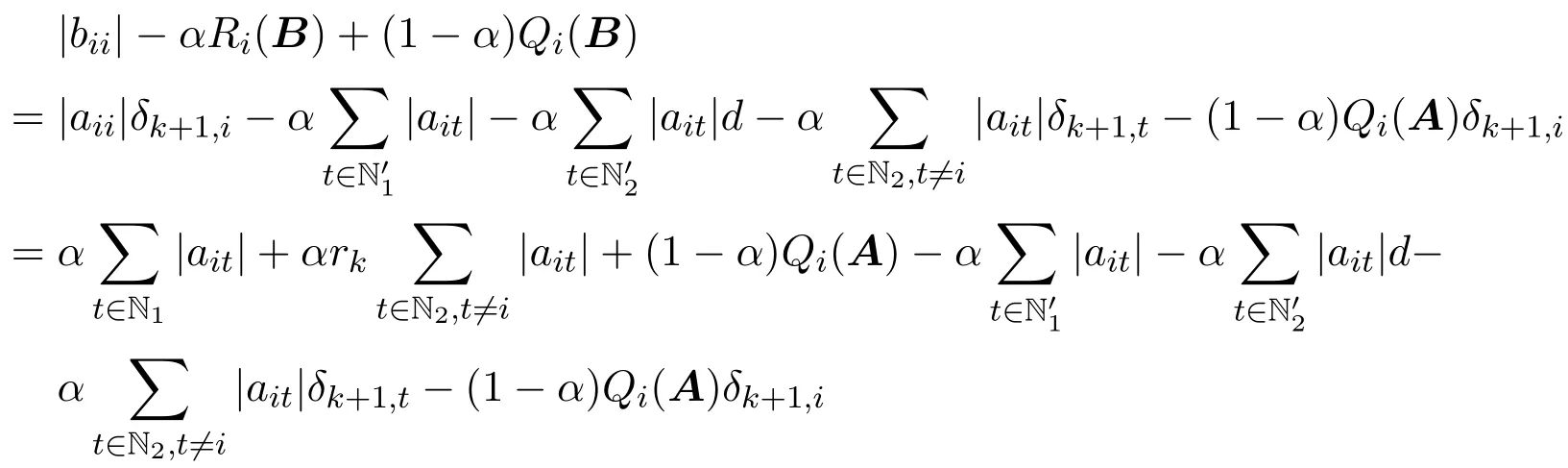
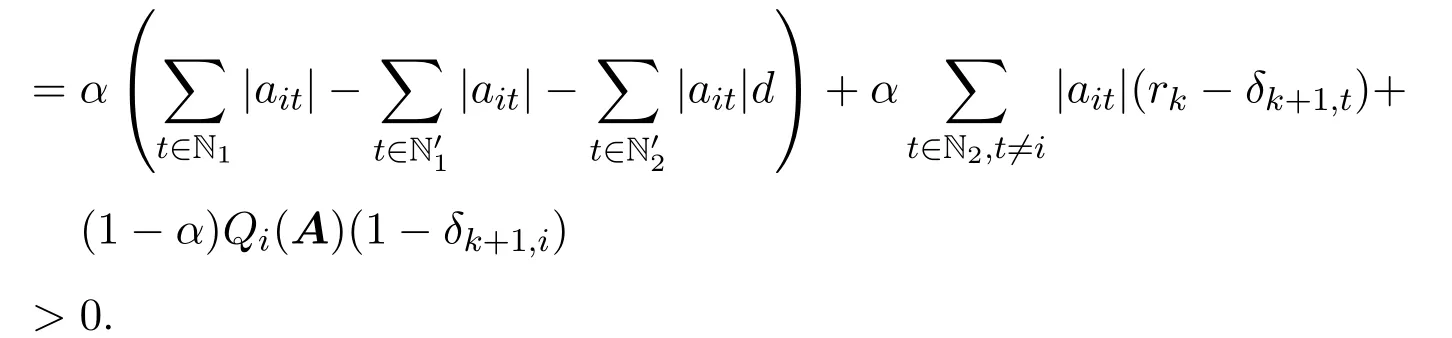

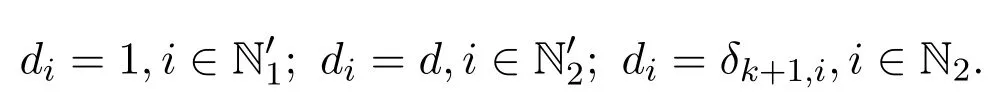




3 数值算法
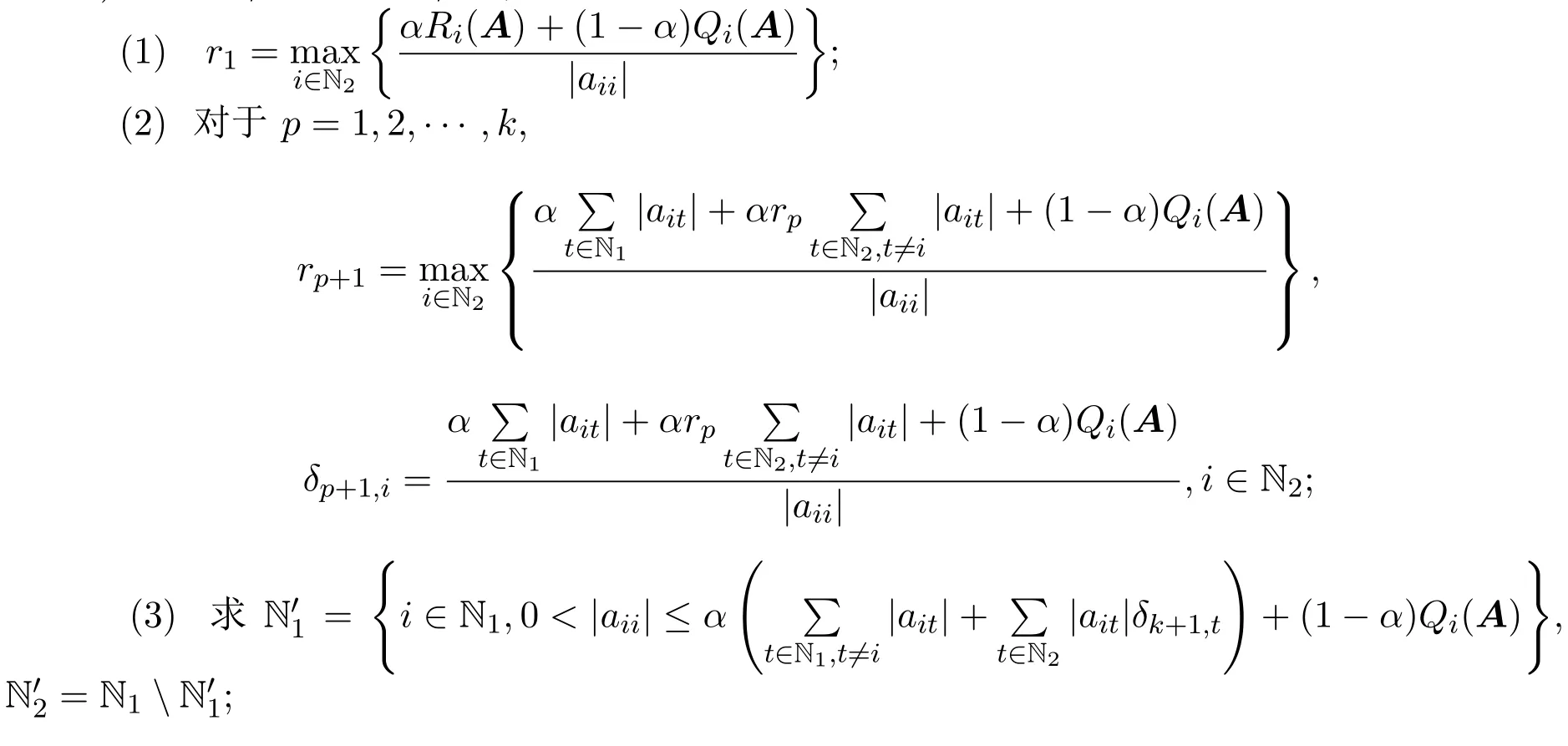
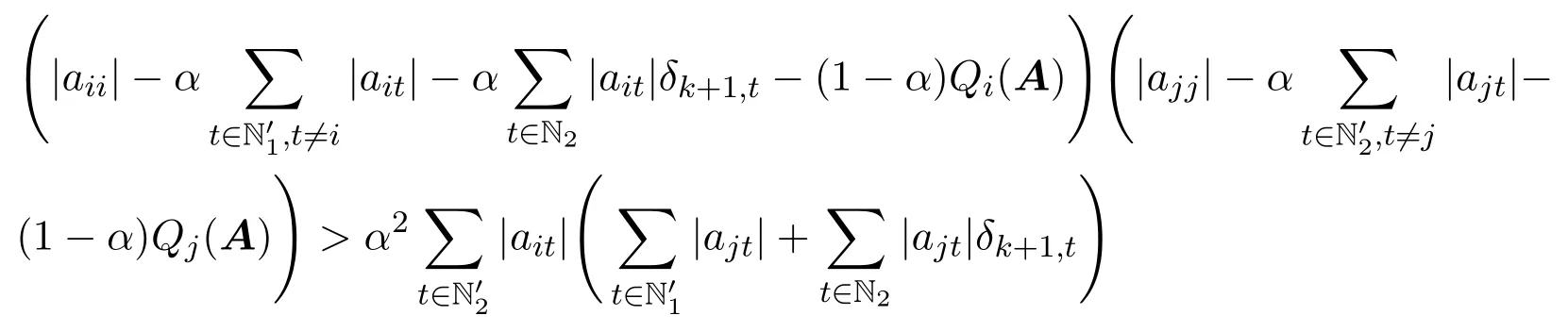
4 数值算例


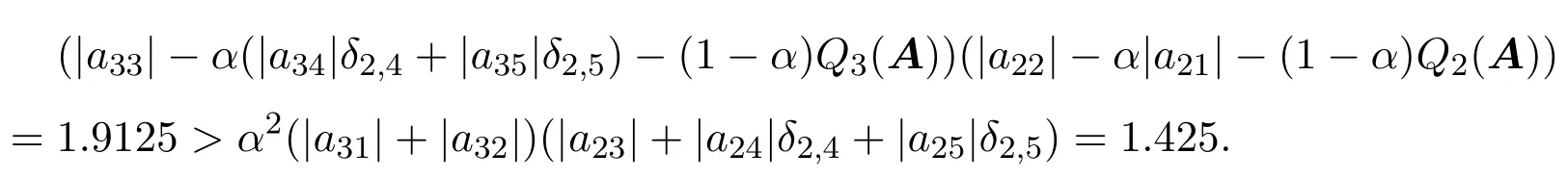
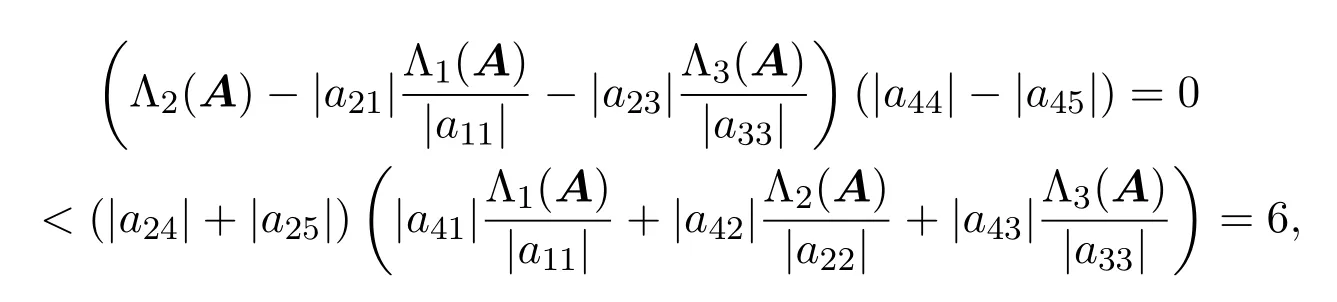
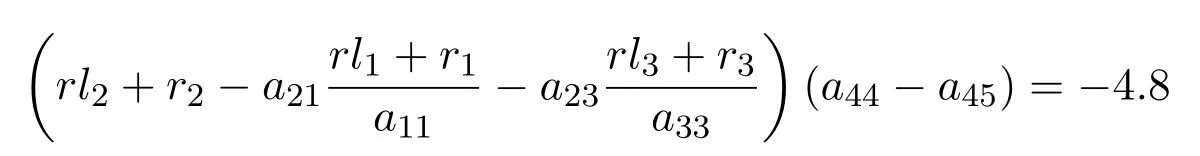



(School of Mathematics,Inner Mongolia University for the Nationalities,Tongliao 028043,China)
