对不规范道路线形参数的取值分析

缪宏兵，杨耀宗

(重庆交通大学 土木建筑学院，重庆 400074)

对不规范道路线形参数的取值分析

缪宏兵，杨耀宗

(重庆交通大学 土木建筑学院，重庆 400074)

结合现有不规则道路运营现状及旧路改建的趋势化，提出将旧路改建问题数学化。综合运用拟合逼近原理，建立旧路改造路线的数学模型。通过对数学模型的不断优化，得到目标线形函数，结合数值计算软件MATLAB程序，对实例模型进行试算，获得较理想的线形参数。结果表明：路线问题数学化得到的拟合参数较合理可靠，可作为相关设计的参考。

改建道路;平面线形;数学模型;曲线拟合;优化

改革开放以来，我国公路建设发展迅猛，技术标准也逐渐提高。然而，据不完全统计,到目前为止尚有过半不规则低等级道路在服役中，这些低等级公路已难以适应社会发展的需要，因此道路改造任务十分繁重。较之于新路的修建，在道路改造中一般考虑如何最大限度的利用原有道路[1]，减少工程量，以达到最佳的经济效益，同时又要使公路的线形符合设计标准，达到提高等级的目的，这就涉及到线形参数取值问题。

1 建模分析

1.1 问题转化

如图1，设在点O处测定的坐标为O(x″,y″)，根据设计公路的等级要求设定常数D为不同的值，根据下列公式，求得测定的坐标点数：

(1)

则求得测定各点的坐标为p(x″,y″)(i=0,1…N)。

根据上述描述，可以先利用原路线的形状初步确定交点的位置，比较清楚的描述直线段的位置。现在的主要任务是确定缓和曲线—圆曲线—缓和曲线的轨迹, 确保曲线与曲线相切。为了不失一般性，取一段曲线OS对其进行分析。要求缓和曲线两端分别与直线和圆相切，取其中一个切点为坐标原点建立右手直角坐标系，则切点分别为O、P、Q、S(见图1)，两条直线夹角为α，交点为R(d,0)，其中：T(x0,y0)、S(a,b)、P(x1,y1)、Q(x2,y2)，可认为α已知，需要建立数学模型，求解T、S、P、Q点坐标。

图1 曲线的组成Fig.1 Curve construction

根据路线规范，直线段与缓和曲线、缓和曲线与圆曲线、圆曲线与缓和曲线、缓和曲线之间都是相切的[2]，这样，图1中的整个曲线可以利用分段函数来表示：

(2)

式中：g1(x)为图1中左边分别与直线段、圆曲线段相切的缓和曲线，g2(x)为图1中分别与两边的缓和曲线相切的圆曲线，g3(x)为分别与圆曲线和缓和曲线相切的缓和曲线。

1.2 模型的假设

(1)原线路的路面视为均质等宽;

(2)道路的改造只与利用度有关，其他因素概不考虑;

(3)为方便，将旧路简化为二维，不考虑地面竖向斜坡的角度对线路优化的影响。

1.3 旧路路线的确定

对于现代道路平面线形，考虑到一般性，选择直线、圆曲线、缓和曲线作为基本型[3]。在公路的改造定线过程中，当工程量增加不大而又能显著提高技术指标时，应以改建为主；当提高技术指标有限又会显著增加工程量时,应以利用为主[4]。一般可利用原路线形直线段，并初步定出交点的位置。

初步确定交点时主要考虑交点的密度、旧路直线段的选取和综合。带状图大致确定路线方案，初步确定路线交点。确定的方法是分析旧路可以利用的直线路段，根据直线路段确定交点导线各边的基本位置。可以通过自作程序输入各交点的坐标，直接求出导线边长和偏角。确定交点需要注意：第一、交点的间距应当大于两端最短切线的长度；第二、交点处的旧路线形状应当便于配合一个某种规则的曲线。在交点确定的基础上，一个交点的曲线可以使用以下算法生成。

1.4 路线的分析

1.4.1 对样条函数g1(x)分析[5]

缓和曲线主要有回旋线、二次抛物线及双纽线。我国标准规定缓和曲线采用回旋线，回旋线的基本公式为：

(3)

式中：r为回旋线上某点的曲率半径；l为回旋线上某点到原点的曲线长；A为回旋线的参数。在回旋线上任一点P取微分单元，则有：

(4)

通过微积分转化有：

(5)

1.4.2 对样条函数g2(x)分析

由图1可知，圆心坐标为T(x0,y0)、半径为R。则圆的方程为：

(6)

又由于圆曲线是圆的一部分，故有：

(7)

1.4.3 对样条函数g3(x)分析

从图2分析知，由g1(x)到g3(x)相当于将回旋线旋转α角，再做y轴对称曲线另外，平移到S(a,b)。由解析几何知识可知：

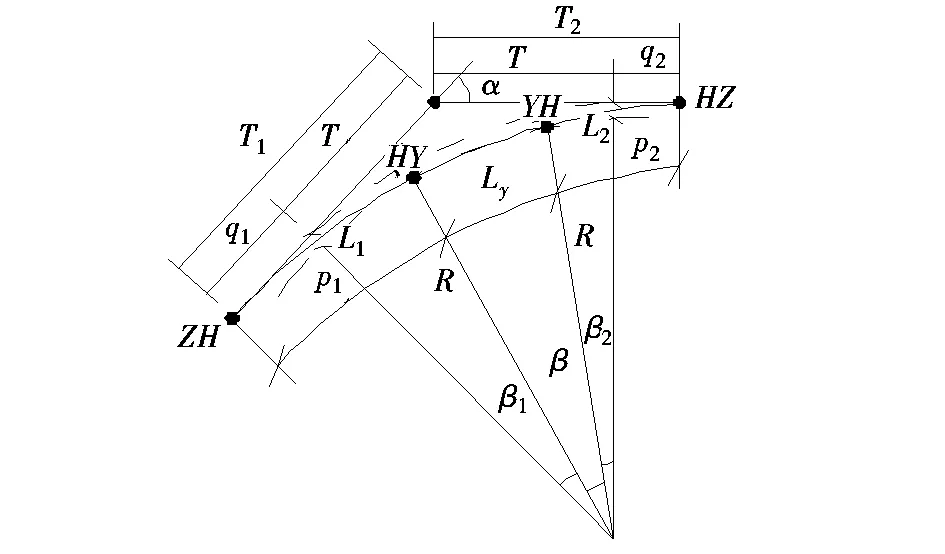
图2 缓和曲线Fig.2 Transition curve

(8)

1.4.4 确定模型中l1、l2取值范围

对于上述的样本函数，只要确定变量C1、R、C2的大小，那么样本函数就可确定。又因上述一些函数是无穷级数，在后面建立的模型中很难求解，故有作进一步简化的必要。

对上述参数方程的分析可知，g1(x)函数均是交错幂级数，而且相邻的两项相近，故幂级数可用多项式近似表示为[4]：

(9)

又由于样本函数g3(x)由g1(x)推导得到的，故其幂级数也可用多项式近似表示为：

(10)

在线路确定时，首先确定转角α，故转角α已知。另外，根据本模型的思路，先对C1、R、C2赋不同的值，比较目标函数的大小，则C1、R、C2可以认为是已知的。

(11)

由图1分析知，切点P(x1,y1)在圆曲线上，故有：

(12)

同时P点也在缓和曲线上，故有：

(13)

联立(2)、(3)求得：

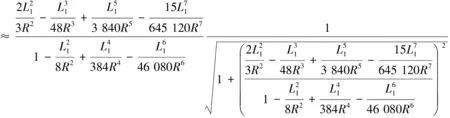
(14)

同理：

(15)

显然，通过切点求得各变量的关系。

另有，直线PT与切线垂直，故有：

(16)

由上述求得x0代入上式，即可求得y0值。

由图2几何关系分析知：

(17)

(18)

由于x0、y0、γ1、γ2均已求出，故在上两式中只有a、b为变量，联立(17)、(18)求得：

(19)

将(19)式代入(17)式即可求得b值。

1.5 线形优化

在问题分析中，已经比较清楚地讨论了实现最佳经济效益的途径，即改造后的路线尽可能地与原线形重合，这样可以表示为，在使用设计线路的里程系统条件下，样本函数与旧路离差的平方和为最小。即

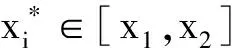
其中公路设计中的一般规定有：Ci∈[100,

50 000],i=1,2.R∈[100,1 000]

2 实例分析

上述模型，思路清晰、方法简洁，但从模型的目标函数来看，求解比较麻烦，只能借助数学软件MATLAB编制程序来求解。

已知某乡村道路，交点坐标为(98 723，98 237)，左边、后边的方位角分别为80°、30°。设改道路为一条不规则曲线，由以下离散点定义见表1。

表1 原道路中线离散点坐标

假设C1和C2的起算值均取400 m2，步长为5 m；R起算值为100 m，步长为10 m。经过编程计算，求得的优化结果为：C1=45 079.78 m2,C2=23 158.75 m2,R=180.24 m。

3 结论

将不规则线形道路改建问题转为数学模型，运用先进的数学方法及计算机技术进行求解，得到相关结论：(1)数学模型中对缓和函数作了一些近似处理，故省略了后面的多项式，得到的结果有一定的误差；(2)该数学模型经实例论证是可行的，只是模型略复杂，若综合利用程序求解，可得较合理的拟合参数，因而可作为相关设计的参考。

[1] 杨进，孙剑峰.改建公路平面线形设计[J].湖南交通科技，2002，28(3)：15-16.

[2] 中交第一公路勘察设计研究院.JTG D20-2006，公路路线设计规范[S].北京：人民交通出版社，2006.

[3] 周广奇.改扩建道路线形拟合设计[D].西安：长安大学，2011.

[4] 刘成志，张步才.基于既有道路改建路线测设和曲线拟合方法的探讨[J].西南公路，2006(4)：24-25.

[5] 李乃成.数值分析[M].北京:科学出版社，2011.

(责任编辑：张英健)

Analysis on Irregular Road Alignment Parameter Value

MIAO Hongbing，YANG Yaozong

(School of Civil Engineering & Architecrure，Chongqing Jiaotong University，Chongqing 400074,China)

Combined with the existing road reconstruction operation status of irregular and old road the trend, the problems of the old road reconstruction of mathematics are presented. According to fitting approximation principle, a mathematical model of the old road is set up. Through continuous optimization of the mathematical model, a linear function of target is obtained, and numerical calculation software MATLAB program, for example by trial model, obtains the linear parameter ideal. The results show that the fitting parameters route mathematic problem obtained is reasonable and reliable and can be used as a design reference.

road reconstruction; plane geometry; mathematical model; curve fitting; optimization

2014-05-02

缪宏兵(1990-),男，江苏如东人，硕士生，主要研究方向为路桥设计。

U412.3

A

1671-5322(2014)04-0065-05