C余弦函数的概率型逼近问题

李晓敏

(盐城工学院 基础教学部,江苏 盐城 224051)

C余弦函数的概率型逼近问题

李晓敏

(盐城工学院 基础教学部,江苏 盐城 224051)

借助于算子值数学期望以及概率论方法,利用C余弦函数与C半群之间关系、Taylor展开式、Hölder不等式及适当的随机变量矩生成函数等工具,得到C余弦函数概率型逼近表达式及其更一般的结论,并利用推得的结论从生成元的角度给出了C余弦函数概率型逼近的指数公式。

C余弦函数；泰勒展开式；矩生成函数；概率型逼近

近年来算子的表示和逼近得到了广泛的发展,Pfeifer[1-4]给出了C0半群的形式简单而又普遍适用的概率表示式，并提供了这些公式收敛速度的精确估计；陈文忠等[5-6]对于C0半群及C半群概率型的表示做了深入的研究;指数有界C余弦函数的概念由Tanaka[7]引入，同时在C具稠值域时引入了其完全无穷小生成元的概念，并给出了指数有界C余弦函数的生成定理极其对二阶抽象cauchy问题的应用。

本文在半群概率型逼近基础上讨论了指数有界C余弦函数的概率型逼近问题,利用指数有界C余弦函数与C半群之间关系推得的泰勒展开式(引理3)及Hölder不等式，得到了C余弦函数概率型逼近表达式(定理2),从而推出了其更一般的概率型逼近结论(推论1),并利用所得结论从生成元的角度给出了C余弦函数概率型逼近的指数公式(定理3)。

1 C余弦函数的定义及性质

假设X是Banach空间,B(X)为X上的一切有界线性算子的集合,D(A)表示A的定义域,R(A)表示A的值域,C∈B(X)。

定义1[7]设(X,‖·‖)是Banach空间,C∈B(X)为单射,若算子C:R→B(X)满足

(1)C(t+s)C+C(t-s)C=2C(t)C(s),∀t,s∈R；

(2)C(0)=C；

(3)t→C(t)x对每一固定的x∈X在R上是连续的；

(4)存在M,ω≥0,使得‖C(t)‖≤Meω|t|。

则C:R→B(X)称为是X上的一个指数有界的强连续C余弦函数,简称为指数有界的C余弦函数,记作C(t)∈G(M,ω)。

性质2[8]设A是指数有界C余弦函数

C(t)的无穷小生成元,则下面结论成立

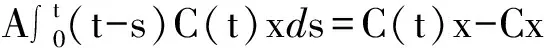
(3)∀x∈D(A),C(t)x∈D(A),且

2 C余弦函数的概率型逼近问题

引理1[2]设S(·)x是可测的,且对所有x∈X其赋值是独立的,若‖S(·)‖≤g(·),其中g(g≥0)是一般意义下的可积函数,则S是广义Pettis可积的,且

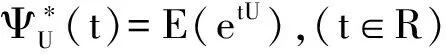
引理3[6](泰勒展开式)设B为C半群

{T(t)}t≥0的无穷小生成元,若x∈D(Br),r≥1,则对∀s,t≥0,有：

T(t)x-T(s)x=

定理1 设A是C余弦函数C(t)的无穷小生成元,A=B2,若x∈D(Br),r≥1,则对∀s,

t≥0,有：

C(t)x-C(s)x=

证明：

C(t)x-C(s)x=

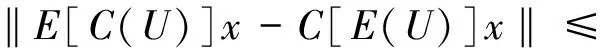
(1)

其中x∈D(A)

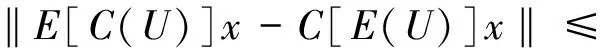
(2)

其中x∈D(A2)

证明：当x∈D(A)时,由Taylor展开式和Hölder不等式,得

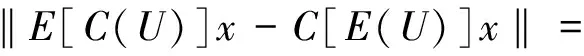
‖E∫tU(U-u)h(u)Axdu‖≤

(1)式得证。

当x∈D(A2)时,由于

C(U)x-C(t)x=

所以

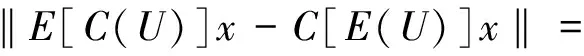
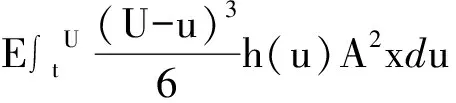
(2)式得证。

类似的,我们可以得到以下推论：

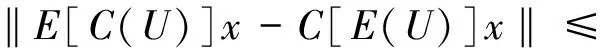
下面从生成元的角度给出一般形式的C余弦函数C(t)概率逼近式及指数公式

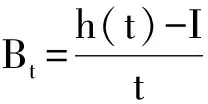
(3)

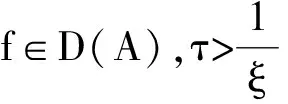
(4)

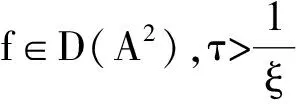
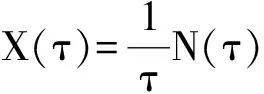
在(1)式中令p=2得

(4)式的证明同(3)式。

从而得出C余弦函数概率逼近指数公式。

[1]PfeiferD.Onaprobabilisticrepresentationforsemigroupsofoperator[J].Math.Esponsition,1984(1):93-98.

[2] Pfeifer D. Approximation theoretic aspect of probabilistic representation for operator semigroups[J].Journal of Approximation theory,1985,43(3):271-296.

[3] Pfeifer D. Probabilistic concepts of Approximation theory in connection with operator semigroups[J].Journal of Approximation theory,1985,1(4):93-118.

[4] Pfeifer D. Butzer P L. A Probabilistic to representation formulate or semigroups of operator with rates of convergence[J].Applicable Analysis,1986，23:111-118.

[5] Chen W Z, Zhou M. Asymptotic formula for probabilistic representations of (C0) operator semigroups[J].Northeast Math, 1994,10(2):159-166.

[6] 陈文忠.C半群概率表示的饱和定理[J].厦门大学学报:自然科学版,1995,34(1):1-6.

[7] Tanaka N. On the exponentially bounded C-cosine family[J].Gokujutsu Kenkyu(Academic Studies),Math,1988,37:37-44.

[8] 郑权,雷岩松.指数有界的C余弦算子函数[J].系统科学与数学.1996.16(3):242-252.

[9] 严士健,刘秀芳.测度与概率[M].北京:北京师范大学出版社,2003:308-309.

(责任编辑：张英健)

Probabilistic Approximations ofCCosine Functions

LI Xiaomin

(Department of Basic Education, Yancheng Institute of Technology, Yancheng Jiangsu 224051, China)

Probabilistic approximations and general conclusion are given forCcosine function by means of operator-valued

mathematical expect and probabilistic methods, using the Taylor expansion given by the association ofCcosine function andCsemigroups' inequality and moment-generating function. Finally, using these given conclusion, the exponential formula of probabilistic approximations forCcosine function is produced by virtue of generator.

Ccosine function；Taylor expansion；moment-generating function； probabilistic approximations

2014-09-29

李晓敏(1978-)，女，江苏徐州人，助教，硕士，主要研究方向为算子半群。

O177

A

1671-5322(2014)04-0018-03