阈值策略下二元对偶风险模型
2014-07-24周金乐王传玉
周金乐,王传玉
(安徽工程大学 数理学院,安徽 芜湖 241000)
阈值策略下二元对偶风险模型
周金乐,王传玉
(安徽工程大学 数理学院,安徽 芜湖 241000)
在阈值分红策略下研究了独立二元对偶风险模型,得出了公司直到破产时刻为止的累积红利期望现值函数所满足的两个积分-微分方程,求出了这种情况下的广义Lundberg基本方程,最后运用Laplace变换得出了微积分的解。
对偶风险模型;阈值分红策略;积分-微分方程;Laplace变换
风险是对损失不确定性的一种度量,现代金融学研究的一个重要课题就是对风险的刻画。精算学是以保险行业的风险为主要研究对象,以概率论、数理统计以及随机过程为主要研究工具,通过建立数理模型来估计、分析未来不确定事件产生的影响,为保险人在现实中进行有效的风险管理和控制提供理论和技术支持。在保险精算数学的范畴内,破产理论是风险理论的核心内容。破产理论研究的是保险人长期的财务状况的变化,更确切地,是研究和监督保险人的盈余随着业务的发展而产生的变化,当盈余为负时则认为破产。但是经典风险模型是一类最简单的随机过程模型,出发点是为了使研究更加方便,而在实际的应用中,这种风险模型往往具有一定的局限性。为此将原来一种索赔情况推广到多种索赔情况使得模型更加贴近于现实情况,对保险公司的决策将会更加有利。文献[1]在经典风险模型的基础上考虑了两类独立的索赔问题,其中第一类索赔次数为一个Poisson过程,另外一类则为更新过程,求出在无限时间的情况下对应的破产概率。
破产理论中的红利问题最早是由De Finetti[2]在纽约第15届精算师代表大会上发表的一篇文章中提出来的,由此便产生了风险理论最前沿也最流行的分支:分红策略的研究。保险公司为了吸引更多的用户,将分红策略考虑进了很多保险业务中,即投保人可以得到传统保单规定的保险责任外,还可以从保险公司经营的利润中获得较高的投资回报。文献[3]就是在Gamma-Omega 模型中考虑了带障碍策略的分红问题,并获得当盈余为负值的时候,公司经过自己的再发展而不能起死回生的破产概率;文献[4]讨论的是在一个复合泊松风险模型中考虑阈值策略,计算出直到破产为止的红利贴现值,以及使得红利贴现值达到最大时的最优阈值;文献[5]推导出经典风险模型中对偶模型下满足总贴现红利期望条件的一类积分微分方程,并以此得出在障碍策略下的红利表达式以及最初盈余和障碍值之间的独立关系;文献[6]在障碍策略下考虑一个广义Erlang(n)对偶模型,获得满足边界条件时股利贴现的期望以及矩母函数所满足的积分微分方程;文献[7]是在文献[5]的基础上将对偶模型从障碍策略情况推广到阈值策略,得出了相似的结论并且得出障碍策略就是阈值策略的极限情况。
本文基于以上情况,在文献[7]的基础上,将原来在阈值策略下对一元对偶模型的研究推广到独立二元对偶风险模型,从而更加贴近于风险多样化和复杂化的现实情况,为科研工作者发明创造所遇到的风险提供了更好的风险刻画和监督。
1 模型介绍
考虑两类收入独立的对偶风险模型,它们的盈余过程可以表示为

(1)
该式中u=U(0)为初始资金;c为花费率;S(t)表示t时刻的总利润。{N1(t);t≥0},{N2(t);t≥0}分别表示收入X与收入Y在[0,t]内收到的收入个数且分别服从参数为λ1与λ2的泊松过程,{Xi;i≥1}和{Yj;j≥1}分别表示收入X与收入Y在第i次与第j次的利润额。{N1(t);t≥0},{N2(t);t≥0},{Xi;i≥1}以及{Yj;j≥1}是两两独立的随机变量序列。设它们的分布函数分别是F(x)与G(y),密度函数分别为f(x)和g(y),均值分别为μx和μy。
对盈余过程考虑一个阈值为b的阈值策略,当U(t)
(2)
设T=inf{t:U(t)=0}表示破产时刻,利息率为δ(δ>0),所以到破产时刻为止总红利的贴现值为
所以直到破产为止总的红利贴现值的期望为

同时令
2 积分—微分方程
2.1 分红函数在0 定理1 当0 (3) 证明:考虑在区间(0,dt]内收入产生的情况,可以分为如下的几种情形: (1) 在(0,dt]内第1类收入X′没有产生收入,第2类收入Y′也没有产生收入,即不产生任何的收入,则其概率为(1-λ1dt)(1-λ2dt); (2) 在(0,dt]内第1类收入X′产生收入,第2类收入Y′没有产生收入,则其概率为λ1dt(1-λ2dt); (3) 在(0,dt]内第1类收入X′没有产生收入,第2类收入Y′产生收入,则其概率为λ2dt(1-λ1dt); (4) 在(0,dt]内两类都产生了收入,则其概率为λ2dtλ1dt=0(dt)。 则当0 (4) 运用二阶泰勒展开式知E[V1(u-c1dt;b)]= (5) 而 (6) 对于 E{V1[(u-c1dt)+z1;b]I[z1∈ (7) 同时 E{V2[(u-c1dt)+z1;b)I(z1∈ (8) 同理可知 (9) 把(5)、(6)、(7)、(8)、(9)代入(4)并经过化简,再将等式两边同时除以dt;并令dt→0,则可以得到(3),即我们所要得到的结果。 2.2 分红函数在b 定理2 当b λ1∫0+∞V2(u+x;b)dF(x)+ λ2∫0+∞V1(u+x;b)dG(x)+c2-c1=0 (10) 证明与定理1的相同,这里省略。 3.1 广义Lundberg方程 由于上面的积分—微分方程的解与广义Lundberg方程的根有关,接下来讨论广义Lundberg方程。记 分别是P(X)与Q(X)的矩母函数。 定理3 上述(4)式所对应的对偶风险模型的广义Lundberg方程为 λ1[MX′(θ)-1]+λ2[MY′(θ)-1]-cθ=δ (11) 证明:由文献[10]中的定理5知道,存在一个δ满足下面的鞅条件 故 当上式等于eθu,即要求 所以它的广义Lundberg方程为 λ1[MX′(θ)-1]+λ2[MY′(θ)-1]-cθ=δ。 注:该模型的广义Lundberg方程有一个唯一的非正根。因为令 所以m(θ)在(-∞,0)是凸的,所以m(θ)具有一个唯一的非正根。 3.2 运用V1(u;b)求V(u;b) 定理4 一个独立二元的复合泊松对偶模型,在没有红利的前提下,它对应的花费率是常数c,那么破产时间T的Laplace变换可以表示为 这里的Rδ是广义Lundberg方程λ1[MX′(θ)-1]+λ2[MY′(θ)-1]-cθ=δ的唯一的非正根。 证明:定义一个过程{Zθ(t):t≥0},其中 定理5 当u>b时,有 (12) 这个证明与文献[7]定理2的证明类似,故省略。 定理6 令z=b-u并且令w(z;b)=V(b-z;b),则 (13) 证明:将(12)式代入(3)式得 所以, 令z=b-u,定义W(z;b)=V(b-z;b)(0≤z≤b),将其代入上面的等式,则 式中,初始条件和边界条件分别是 记w(z)=W(z;b),对上面的方程两边同时运用Laplace变换,则可以得到 即 同理可以得出 所以当c2→+∞的时候 当λ1=0即S2(t)不存在的时候,就与文献[7]中的推论4.1一样,同时当c2→+∞这里的w与在障碍策略下的值相同,也就是说当c2→+∞的时候,阈值策略就是障碍策略。 本文在阈值策略条件下研究了独立二元对偶模型,比一元的情况更加符合实际,很有实际应用价值。本文得出的在二元情况下障碍策略依然是阈值策略的极限形式的结论,从红利方面为投资者投资提供一些指导建议。 [1] Lv T L, Yi J, Zhang G X. Ruin probabilities for a risk model with two classes of claims[J].Acta Mathematica Sinica, English Series, 2010,26(9):1 749-1 760. [2] De Finetti B. Su un′impostazione alternativa della teoria collettiva del rischio[C].Transactions of the XVth International Congress of Actuaries, 1957,2(1):433-443. [3] Albrecher H, Gerber H U, Shiu E S W. The optimal dividend barrier in the Gamma-Omega model[J].European Actuarial Journa, 2011,1(1): 43-55. [4] Cheung E C K, Dickson D C M, Drekic S. Moments of Discounted Dividends for a Threshold Strategy in the Compound Poisson Risk Model[J].North American Actuarial Journal, 2008,12(3):299-318. [5] Avanzi B, Gerber H U, Shiu E S W. Optimal dividends in the dual model[J].Insurance:Mathematics and Economics, 2007,41(1):111-123. [6] Wen Y Z, Yin C C. On a Dual Model with Barrier Strategy[J].Journal of Applied Mathematics, 2012(1):45-58. [7] Andrew C Y N. On a dual model with a dividend threshold[J].Insurance: Mathematics and Economics, 2009,44(2):315-324. (责任编辑:张英健) A Binary Dual Risk Model Under the Threshold Strategy ZHOU Jinle,WANG Chuanyu (Coll.of Math.and Pht., Anhui Polytechnic University, Wuhu Anhui 241000, China) In this paper, we study the binary dual independent risk model under a threshold dividend strategy and derive a set of two integro-differential equations satisfied by the expected total discounted dividends until ruin and find the basic equations of the generalized Lundberg in this case. In the end we use the Laplace transform and obtain calculus. a dual risk model; threshold strategy; integro-differential equations; Laplace transform 2014-06-17 周金乐(1989-),男,安徽芜湖人,硕士生,主要研究方向为金融工程与金融衍生物。 O211.9 A 1671-5322(2014)04-0013-05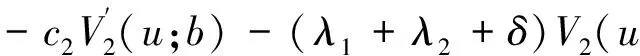
3 运用Laplace变换求V(u;b)
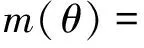





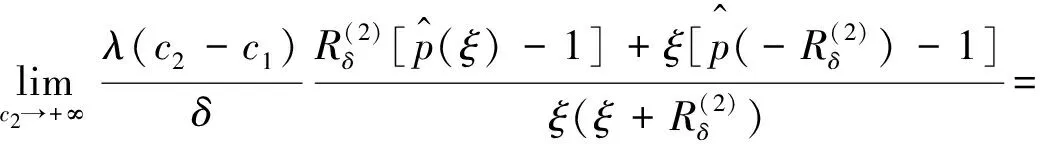
4 结论
