基于粗糙集的增强学习型分类器

郑 周，嵇春梅，赵 斌，刘解放

1.盐城工学院 信息工程学院, 江苏 盐城 224051； 2.盐城工业职业技术学院 机电工程学院，江苏 盐城 224051； 3.北京工业大学 计算机学院,北京 100022

基于粗糙集的增强学习型分类器

郑 周1，嵇春梅2，赵 斌3，刘解放1

1.盐城工学院 信息工程学院, 江苏 盐城 224051； 2.盐城工业职业技术学院 机电工程学院，江苏 盐城 224051； 3.北京工业大学 计算机学院,北京 100022

为了提高分类的精确度，提出一种基于粗糙集理论的增强学习型分类器。采用分割算法对训练数据集中连续的属性进行离散处理；利用粗糙集理论获取约简集，从中选择一个能提供最高分类精确度的约简。对于不同的测试数据，由于离散属性值的变化，相同的约简可能达不到最高的分类精确度。为克服此问题，改进了Q学习算法，使其全面系统地解决离散化和特征选择问题，因此不同的属性可以学习到最佳的分割值，使相应的约简产生最大分类精确度。实验结果表明，该分类器能达到98%的精确度，与其它分类器相比，表现出较好的性能。

粗糙集；增强学习；属性约简；离散化；特征选择

分类问题是数据挖掘领域中应用和研究最为广泛的技术之一。如何更精确、高效地分类一直是广大科研人员的目标[1]。目前监督和无监督学习[2-4]作为分类技术已得到广泛的应用,支持向量机、决策树、K-近邻、人工神经网络和聚类技术等机器学习方法被应用于分类器。有监督学习，标记训练数据十分耗时；而无监督学习，由于没有足够的先验领域知识，恰当的数据划分变得困难。而且没有技术能够很好地适应实时动态数据分类。

增强学习常用于序列预测和构建分类器。文献[5]提到为了应用增强学习，必须有充足的样本数据用于学习环境，但是，大样本空间使学习过程变慢，导致该方法不适合实时应用；Q学习是一种增强学习技术[6-8]，在一个特定状态且未知环境中，利用经历的动作序列执行最优动作。文献[9]提出分布式增强学习，它以分层的方式工作，每层通过中心代理向更高层发送数据，不过计算量大，且不具有健壮性。

本文提出一种全面的学习方法，该方法集成了粗糙集理论和增强学习(Q学习)算法，具有较高的分类精确度。粗糙集理论仅能用于离散数据，需要分割连续条件属性,它的不可辨别性概念用来选择最重要的属性集——约简，以代表原始数据集。对于不同的测试数据，采用相同的分割值可能产生不同的约简，因此要选择提供最高分类精确度的约简来构建分类器。本分类器中，我们改进了Q学习算法，使其为每个条件属性学习不同的分割值；通过评估相应约简和精确度形成回报矩阵。改进的Q矩阵为每个属性选择最佳分割值，以达到最高的分类精确度。

1 粗糙集理论的属性约简

粗糙集理论(RST)是一种处理模糊、不精确分类问题的数学工具，它提供了一套比较成熟的方法，能够在样本数据集中发现数据属性间的关系,其中知识约简是RST的核心问题之一[10]。

1.1 约简

信息系统是一张二维数据表。它可以形式化为一个四元组IS=(U,A,V,f),U是一个非空对象集,即论域，A是一个非空属性集，A=C∪D且C∩D=φ,C为条件属性，D为决策属性，Va表示a∈A的值域，f:U×A→V是一个信息函数。条件属性集表示对象的特征，而决策属性集表示对象的类别标签。为了从表中消除冗余的和不重要的属性，RST中约简概念应运而生。约简是一个最小的条件属性子集，它足以表示整个数据表。约简不是唯一的，因此发现所有的约简是NP问题。为了寻找近似约简，数据挖掘领域开发了很多新的算法[11-14]。Skrowron[15]引入了差别矩阵的概念，基于差别矩阵的约简由差别函数产生。差别函数利用吸收和扩展律删除冗余属性，生成约简。

1.2 差别矩阵

差别矩阵定义：给定一个决策系统DS=(U,C,D)，U是论域，C为条件属性，D为决策属性。全集U={x1,x2,…,xn}，而差别矩阵M=(mij)是一个|U|×|U|的矩阵，其中元素mij是对象对xi和xj通过公式(1)得到。

(1)

mij为差别矩阵元素，也是条件属性子集，它是第i个个体xi与第j个个体xj属性值不相等的那些属性构成的集合，或说mij是所有能区分开个体xi和xj的属性构成的集合。因此如果mij≠φ，对象xi和xj能被区分。当i=j时，显然mii=φ，因为不存在把样本xi与自身区分开的属性。一个差别矩阵M是对称的，即mij=mji，mii≠φ。因此，只考虑下三角或上三角矩阵。

表1为信息系统，它包括10个对象，5个条件属性a、b、c、d、e和1个决策属性f。 表2为该信息系统的差别矩阵。f(s)为差别函数，它是由表2中所有非空元素构成的合取范式。

通过移除等价项，差别函数可表示如下：

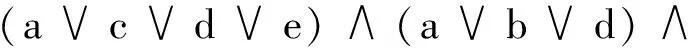
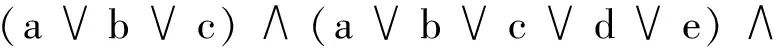
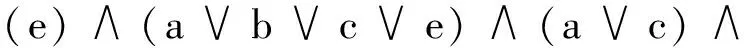
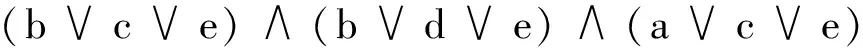
为生成约简，在f(s)上首先应用吸收律。该吸收律规定：如果一项是另一个项的子集，并且两项采用“合取”联结词相连，则保留具有变量个数最少的项。通过运用吸收律，差别函数可化简为f(s)=(e)∧(a∨c)∧(a∨b∨d)。

表1 信息系统

其次应用扩展律，它用来保留那些更频繁地出现在析取项中的条件属性。在具有最高频率的属性上应用“合取”，因为它们在分类中发挥着重要的作用；在出现频率较少的条件属性上应用“析取”，因为考虑所有的条件属性不但不能提高分类精度，反而增加计算复杂度；最后，在每个由“析取”连接的项(析取式)上应用“合取”，所以它们任何一个都可能属于不同的约简。

* 扩展律算法描述：

(1)寻找出现最频繁的属性(至少两次)；

(2)在这样属性上运用“合取”，余下的运用“析取”运算；

(3)运用“合取”连接所有析取式，如果一个项包含(1)中的属性，则消除；

(4)使用“合取”连接由(2)和(3)得到的项。

举例,假如出现最频繁的属性是a，基于扩展律可得：

(1)：a(2)：a∧e

(3)：c∧(b∨d)

(4)：(a∧e)∧(c∧(b∨d))

所以：

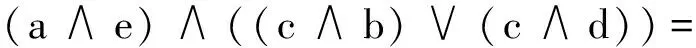
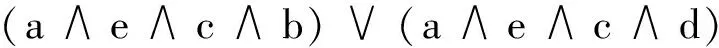
因此，约简是{a,e,c,b}和{a,e,c,d}

2 改进的Q学习算法

本文改进了Q学习算法，并且在NSL-KDD数据集上进行了分类测试。

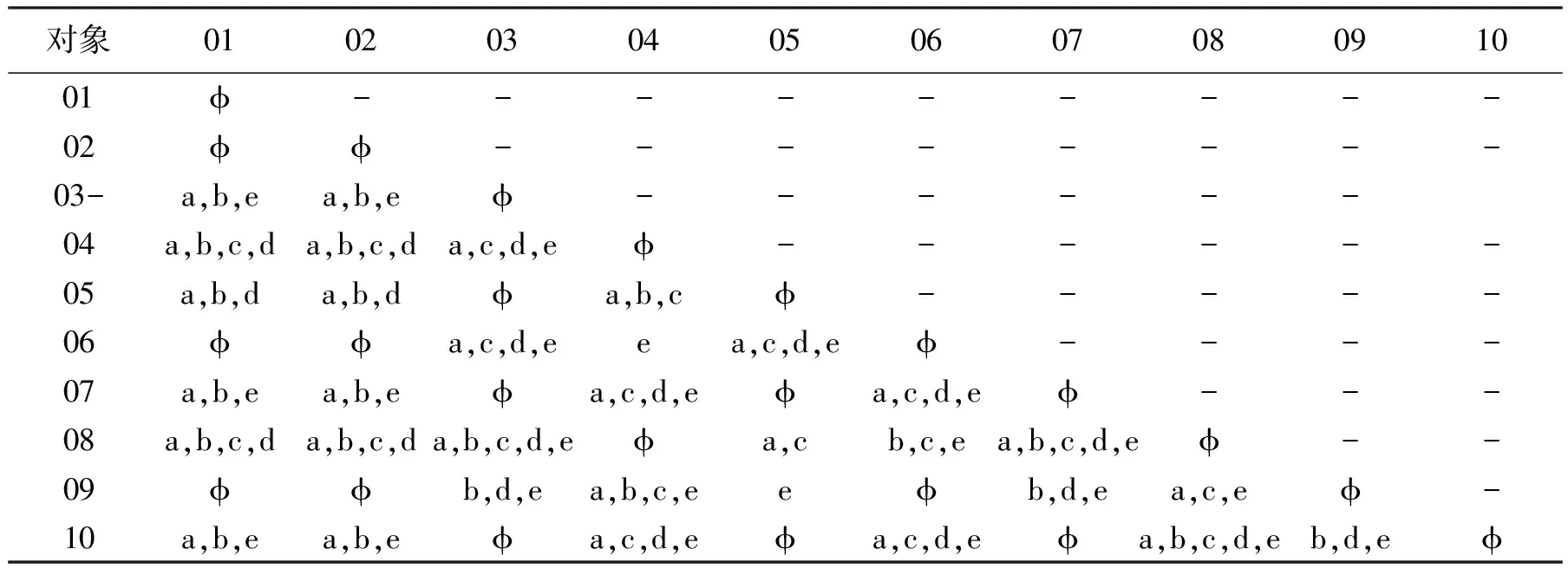
表2 信息系统(表1)的差异矩阵

2.1Q学习算法

Q学习算法[5]是一种广泛使用的增强学习算法。回报矩阵(R)是Q矩阵的组成部分，它把状态映射为行，动作映射为列。学习算法在一个特定的状态下执行最可能的动作，来达到代理指定目标状态。算法的训练是通过“试错法”到达目标状态来学习环境。

增强学习算法有3个主要组成部分，即环境、增强函数和价值函数。根据环境中状态(s)和动作(a)，估计状态-动作对(s,a)的值来构建回报矩阵。通过公式(2)描述的状态-动作对(si,a)的Q值，回报矩阵来构造Q矩阵。Q值决定代理在特定的状态si可能采取的动作，以便下一个状态si+1接近目标状态。回报矩阵形成以后，Q矩阵是通过使用一个学习参数γ，经过有限次的迭代而获得。通过考虑在一个特定的状态下的所有动作，计算得到Q的最大值。

(2)

2.2 回报矩阵的形成

在改进的Q学习算法中，回报矩阵分2个阶段形成：初始化回报矩阵和最终回报矩阵。首先在数据集的所有属性上应用一个特定的分割，把连续属性集离散化，并使用基于RST的差别矩阵概念，生成约简。分类规则来自每个约简，通过设计一个基于规则的分类器来计算相应约简的精确度。选择提供最高精确度的约简，在特定的状态或分割中表示为最佳动作。运用不同的分割，约简相继生成，并估计其精确度，直到两次连续的分割提供相同的精确度或单调递减。精确度是一个阈值，由它确定rij的值。

(3)

redi是分割i提供的最高精确度，初始回报矩阵表示如下：

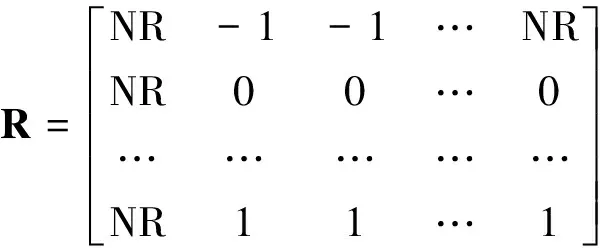
从R中可以发现算法采取的动作仅基于最重要的属性(约简)，而其它的属性不起作用，在矩阵R中，用NR表示。

最终的回报矩阵RF是通过删除R中所有行都是NR值的列，此时，RF矩阵的维度才能确定，它少于R。如果一个特定的属性(列)不属于约简，而RF把它作为自身一个特定的分割(行)成员，则设其值为-1，表明不重要的属性。

* 初始回报矩阵R的算法：

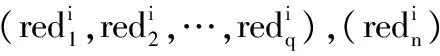
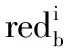
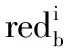
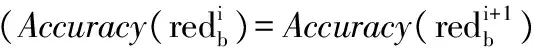
* 最终回报矩阵RF算法：

输入：初始回报矩阵R(n×m)

输出：最终回报矩阵RF(n×p),p≤m

Step1：对于每一个m，确定所有的rij是否为NR。

a=0;

forj=1 tom

Counter=0;

Fori=1 ton

ifrij=NR

Counter++

End for

if counter==行数

Deleted-columna++=j;/*a是一个删除列的索引，用来记录应删除的列*/

End for

Step2：删除c∈Deleted-column[] //c是应该删除的列，其所有行都为NR。

p=0;

Forj=1 tom

flag=0;

Fork=1 toa

Ifj==Deleted-column[k]

Set flag=1;

End for

if flag==0

Begin fori=1 ton

rip=rij;

End for

p+=1;

End for

Step3：用-1替换R矩阵中其余NR元素。

Fori=1ton

Forj=1top

Ifrip==NR;

rip=-1;

Endfor

Endfor

2.3 改进的Q学习算法

从最终回报矩阵形成了矩阵Q，最后1行的所有元素(不包括最后1行都是由零组成)，表示最大分类精度将达到的目标状态。改进学习过程包含若干个步骤，通过步骤6的迭代，直到改进Q矩阵的所有元素都大于0，表示精确度可接受。

*Q矩阵算法：

输入：最终的回报矩阵RF(n×p)

Step1：初始化Q矩阵QM(n×p)，及其所有元素为零。

Step2：给QM的第n个状态(目标状态)赋值。

For(j=1top)

QM[n,j]=RF[n,j];

End

Step3：从RF(n×p)导出稀疏矩阵SM(r×3)，用来记录RF中rij的i(i=1,2,…,n)，j(j=1,2,…,p)和值0/1。

Step4：记录无动作的i(i=1,2,…,n)。

no-action-size=0;

Fori=1 ton

Flag2=0;

Forj=1 top

if RF[i,j]≥0

Flag2=1;

End for

if Flag2=0

no-action[no-action-size++]=i;

End for

Step5：初始化Flag[]，并赋值为零。

Step6：启动运行事件。

Do

Count=0;

/*从i=0(开始状态)开始运行，直到i=n(目标状态)结束*/

While SM[count,0]!=(n-1)

State=SM[count,0];

If (SM[count,2]==0)and(Flag[state]==0)

action-nmber=SM[count,1];

Calculate MAX[QM(next-state,all-actions)]

Update the Q矩阵

QM[state,action-nubmer]=RF[state,action-number]+(γ*Max);

Update 稀疏矩阵SM(r×3)

重新初始化Flag[]数组，赋值为零。

/*检查QM[][]的所有值是否已更新*/

Flag-end=0;

Fork=1 toa

if SM[k,2]==0

Flag-end=1;

End for

Loop until Flag-end==1

Step7：输出Q矩阵Q(n×p)。

初始回报矩阵R、最终回报矩阵RF和Q矩阵如下所示。表3给出了数据集信息系统的部分对象。

表3 NSL-KDD数据集信息系统的部分对象

应用改进的Q学习算法后，Q矩阵被更新形成最终的Q矩阵(Qfinal)其中对于每个j，标出最高的qij值，表示对于属性j，i是最佳的分割值。在Qfinal中，1.64是第1列中最大值，对应于属性CA2；它出现在第2行，对应于分割值5。因此，当对表3进行分类时，达到最高的精度应是在属性CA2采用分割值为5。

初始回报矩阵R：

CA2CA3CA4

初始Q矩阵：

CA2CA3CA4

最终Q矩阵Qfinal：

CA2CA3CA4

3 合成数据集的实验结果

通过评估皮尔逊相关系数对数据集间的相关性进行研究，定义如下：

其中x和y是两个变量，n表示样品的，r的值域为[-1,1]。如果x和y有很强的线性正相关，r接近1；如果x和y有很强的线性负相关，r接近-1；如果它们不存在相关性，r为0。

我们在此选取了合成数据集作为测试数据，其中包括紧密相关的、中度相关和不相关的使用本文设计的分类器对其进行分类，并计算其精确度。数据集的相关性和精确度在表4中列出。从中可以发现当相关性趋于0时，精确度下降，因此，我们的分类器能够分类不同数据集。

表4 不同数据集的相关性和精确度

4 性能验证

本文使用NSL-KDD数据集[16]用于学习环境，它包含42个属性，其中41个是条件属性，1个是决策属性。41个条件属性中，34个是连续的，7个是离散的。将最初相同的分割值应用到所有连续条件属性上，在每个情况下生成约简。例如，考虑200个对象作为训练数据集，应用分割值2，生成4个约简。采取100个对象作为测试数来计算约简的精确度，如表5所示。由于所有约简都显示相同的分类精确度，所以可采用约简R0构造初始回报矩阵。

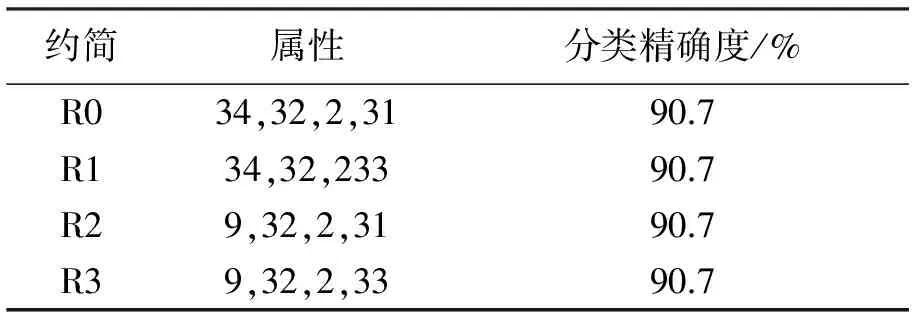
表5 约简与精确度

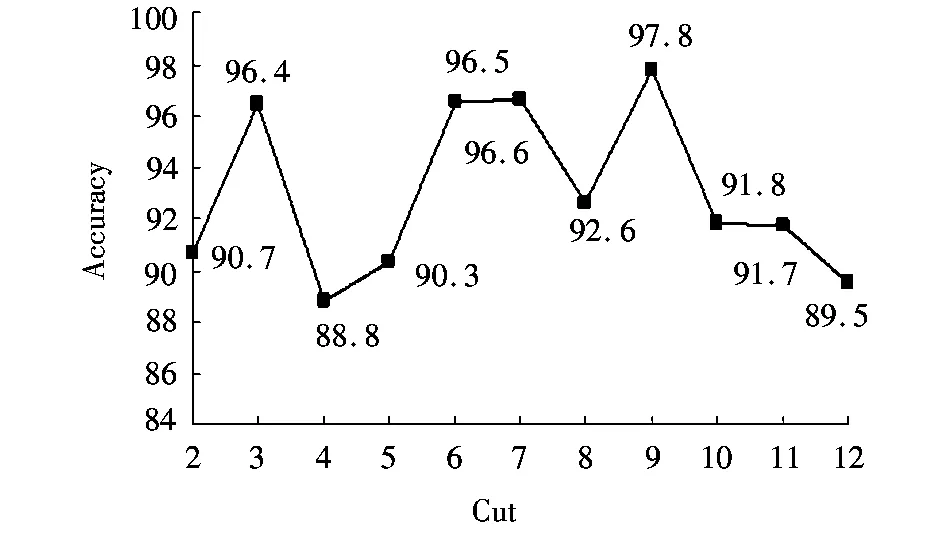
图1 分割值与精确度Fig.1 Partition value and accuracy

重复同样的步骤对所有连续属性施加分割3～9，选择最高分类精确度的约简构造初始回报矩阵。回报矩阵分割或行的个数是由分割产生过程的终止条件确定。图1分割值与精确度显示了对应分割9，10，11的精确度单调递减，所以初始回报矩阵的行数确定为8，定义目标状态相应的分割为9。例如，应用分割3，选择约简R2={2,3,9,21,22,29,35}，它可达到最高分类精度96.4%。

最后，使用属性4,5,9,22,28,29,31,32,33,34,35形成最终的回报矩阵的列，如表6所示。因此，最终的回报矩阵有8行11列。通过应用改进Q学习算法，得到最终Q矩阵，如表7所示。最终Q矩阵中，不同属性的分割来自其对应的最高精确度，例如，属性4对应分割9，属性5对应分割6等被选择为最佳分割值，并应用在新的数据集上，可提供分类精确度高达98.2%。

通过工具WEKA运用10倍交叉验证模型比较本文设计的分类器和其它分类器的分类精确度，结果如表8所示。

表6 最终回报矩阵

表7 最终Q矩阵(最佳分割值生成)

表8 分类精确度

此外，为了评估分类器的鲁棒性，我们在NSL-KDD数据集上选定了一些未知攻击，进行同样的实验,表9给出了实验结果。从表9中可以得出，分类器具有较高的检测率、低的误报率和低的漏报率。F1测度为0.97，这证实了该分类器检测精度高，并证明其良好的性能。

总之，该分类器能够很好的检测到新型的攻击，具有非常高的F1测度(0.97)和低误报率。

表9 性能情况

5 结语

本文采用粗糙集理论和增强学习技术，通过改进Q学习算法实现了一种新的分类器，它能更好地处理离散化、特征选择和精确度计算，从而降低计算成本，实现了更全面地构建分类器。我们发现对于连续属性的离散化，如果所有属性采用相同的分割，即使连续的两个分割值，分类精确度差别很大，但不同属性的不同分割的结合却产生了最好的分类精确度。采用不同的相关数据集测试了我们的方法，表明了该分类器的有效性。实验结果表明，该分类方法实现了较高的分类精确度达80%；具有较高的召回率和F1测度。

本文进一步的工作是继续优化算法，将其应用于大数据集并提高处理大数据的效率。对算法进行个性化持续改进。

[1] 姚亚夫,邢留涛.决策树C4.5连续属性分割阀值算法改进及其应用[J].中南大学学报:自然科学版,2011,42(12):3 772-3 776.

[2] Garla V, Taylor C, Brandt C. Semi-supervised clinical text classification with Laplacian SVMs: An application to cancer case management[J].Journal of Biomedical Informatics, 2013,46(5):869-875.

[3] 舒振球,赵春霞,张浩峰.基于监督学习的稀疏编码及在数据表示中的应用[J].控制与决策,2014,29(6):1 115- 1 119.

[4] Bavdekar V, Shah S. Computing point estimates from a non-Gaussian posterior distribution using a probabilistick-means clustering approach[J].Journal of Process Control, 2014,24(2):487-497.

[5] Lazaric A, Ghavamzadeh M. Bayesian multi-task reinforcement learning[C].proceedings of the 27th Annual Int Conf on Machine Learning. New York: ACM, 2010:599-606.

[6] 赵凤飞,覃征.一种多动机强化学习框架[J].计算机研究与发展,2013,50(2):240-247.

[7] Tong Z, Xiao Z, Li K, et al. Proactive scheduling in distributed computing—Areinforcement learning approach[J].Journal of Parallel and Distributed Computing, 2014,74(7):2 662-2 672.

[8] Jaksch T, Ortner R, Peter A. Near-optimal regret bounds for reinforcement learning[J].Journal of Machine Learning Research,2010,99(8):1 563-1 600.

[9] Servin A. Kudenko D. Multi-agent reinforcement learning for intrusion detection[C]. Proceedings of the 6th German Conference on Multiagent System Technologies, Berlin:Springer Verlag Berlin Heidelberg, 2008.

[10] 石洪波,柳亚琴.一种基于属性分割的产生式/判别式混合分类器[J].计算机应用研究,2012,29(5):1 654- 1 658.

[11] Kumar D A, Sil J. An efficient classifier design integrating rough set and set oriented database operations[J].Applied Soft Computing, 2011,11(2):2 279-2 285.

[12] 刘解放,赵斌,周宁.基于有效载荷的多级实时入侵检测系统框架[J].计算机科学,2014,41(4):126-133.

[13] Liu D, Li T R, Liang D C. Incorporating logistic regression to decision-theoretic rough sets for classifications[J].International Journal of Approximate Reasoning, 2014,55(1):197-210.

[14] 衷锦仪,叶东毅.基于模糊数风险最小化的拓展决策粗糙集模型[J].计算机科学,2014,41(3):50-54,75.

[15] Skowron A, Rauszer C. The discernibility matrices and functions in information systems[M]∥Huang Shi-Yu (Ed.). Intelligent Decision Support-Handbook of Applications and Advances of the Rough Sets Theory. Springer Netherlands, 1991：331-362.

[16] ISCX. The NSL-KDD Data Set[EB/OL].(2012-08-02)[2014-04-20].http://iscx.ca/ NSL- KDD.

(责任编辑：李华云)

启 事

本刊已入编《中国学术期刊(光盘版)》、“中国期刊网”、“万方数据——数字化期刊群”、《中国科技期刊数据库》和《CEPS华艺中文电子期刊》，作者著作权使用费在本刊稿酬中一并给付(另有约定者除外)。对此不同意者，请在来稿时说明。

Reinforcement Learning Classifier Based on Rough Set

ZHENG Zhou1，JI Chunmei2，ZHAO Bin3,LIU Jiefang1

1.School of Information Engineering, Yancheng Institute of Technology, Yancheng Jiangsu 224051, China； 2.College of Electromechanic Engineering, Yancheng Industry Professional Technology Institute, Yancheng Jiangsu 224051, China; 3.School of Computer Science, Beijing University of Technology University, Beijing 100022, China

In order to improve the accuracy of classification, a reinforcement learning classifier based on rough set theory is proposed. First, the continuous attributes in the training data set are discretized by using segmentation algorithm. Second, reducts are obtained by using the rough set theory and finally, one of the reducts providing the highest classification accuracy is chosen. But for the different test data, the same reducts may not reach the highest accuracy of classification because of the changes of discrete attributes value. To overcome this problem, Q-learning algorithm of the reinforcement learning is modified and it can comprehensively and systematically solve the problem of the discretization and feature selection and make different attributes to learn to the best cut value so that the corresponding reducts can produce the maximum accuracy of classification. Experimental results verify that the classifier achieves the accuracy of 98% and exhibits excellent performance compared with other classifiers.

rough sets; reinforcement learning; attribute reducts; discretization; feature selection

2014-06-11

国家自然科学基金资助项目(61272500)

郑周(1984-),男，江苏徐州人，讲师，硕士，主要研究方向为计算机网络、网络安全、物联网技术。

TP393

A

1671-5322(2014)04-0047-08