导体在含有电阻、电容、电感导轨电路上的运动规律探析

梁明智

（赤峰学院 物理与电子信息工程系， 内蒙古 赤峰024000）

导体在含有电阻、电容、电感导轨电路上的运动规律探析

梁明智

（赤峰学院 物理与电子信息工程系， 内蒙古 赤峰024000）

本文分析讨论了在含有电阻、电容、电感导轨电路上导体的运动规律，发现接电阻、电容和电感时导体棒的运动规律是不同的，对于接电阻时，最终导体棒将作匀速直线运动；接电容时，导体棒最终将作匀加速直线运动，而接电感时，根据电阻的不同，导体棒最终也将作匀速直线运动.

电流；节点；初始值；终了值；拉普拉斯变换

在电磁学中，经常会涉及在倾斜的光滑导轨上接有电阻、电容或电感时，放在导轨上的金属棒的运动规律问题，下面就这一问题进行详细的讨论.

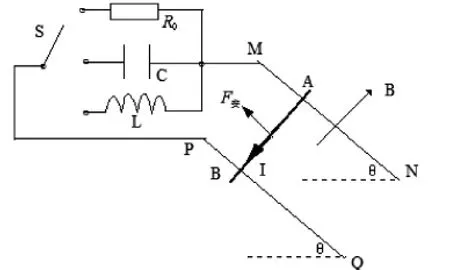
设地面上有一与水平面成θ角的固定光滑导轨MN和PQ，两导轨的间距为L0，其电阻可略，空间存在有与导轨平面垂直的匀强磁场，磁感应强度大小B，一质量为m，电阻为R的导体棒AB放在导轨上并和导轨有良好的接触.下面讨论开关S分别与电阻、电容或电感相连时导体棒的运动规律.

1 开关S与电阻R0相连

设t=0时将导体棒由静止释放，t时刻时棒沿导轨向下的速度为V，则根据电磁感应和牛顿第二定律有：

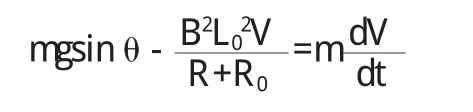
当t=0时，V(0)=0，则该方程的解为：

（2）最终导体棒将作匀速直线运动，其速度为：

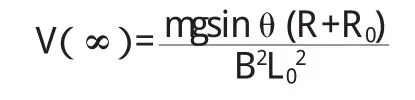
2 开关与电容C相连

设电容开始时所带的电荷量为0，t=0时将导体棒由静止释放，t时刻时棒沿导轨向下的速度为V，此时电路中的电流为I，电容两端的电压为uc，则根据基尔霍夫定律和牛顿第二定律有：

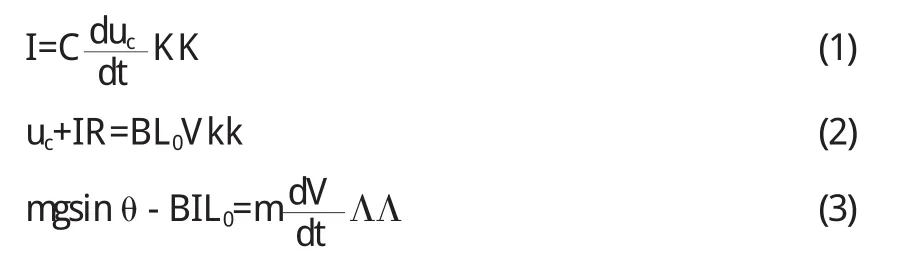
整理后有：

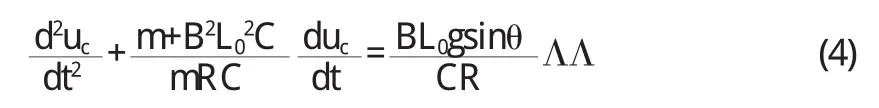
解有：

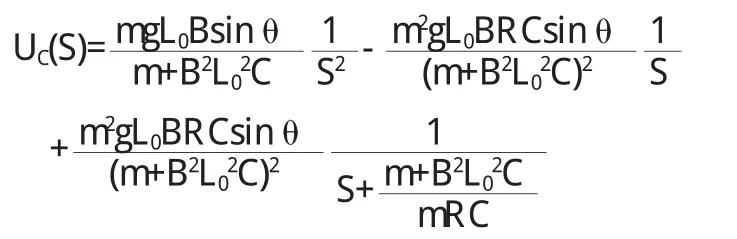
对UC(S)求反拉普拉斯变换有：

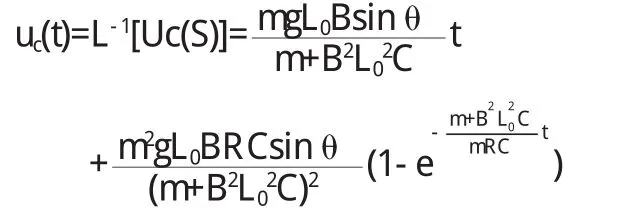
由(2)式得导体棒的速度为：

下面对导体棒的速度进行如下讨论：

（1）导体棒的运动可理解为匀加速直线运动与速度按指数规律增加运动的合成，若令，可知τ越大，导体棒的速度增加的越慢，而τ的大小只取决于电路本身与初始条件无关.

（2）若t>>τ时导体棒运动速度为：

由(6)式可知导体棒最终将作匀加速直线运动.

（3）若回路电阻R=0，则导体棒开始就作匀加速直线运动，其加速度为

3 开关与电感L相连

在t=0时将导体棒由静止释放，t时刻时棒沿导轨向下的速度为V，此时电路中的电流为I，则根据基尔霍夫定律和牛顿第二定律有：

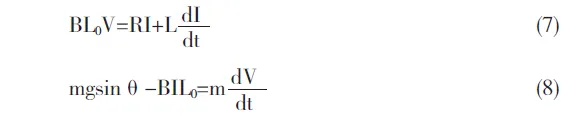
由（7）、（8）式整理得：

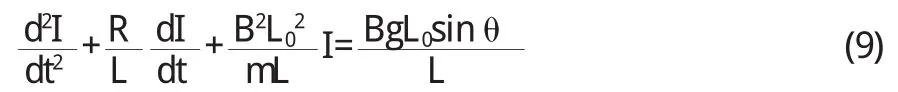
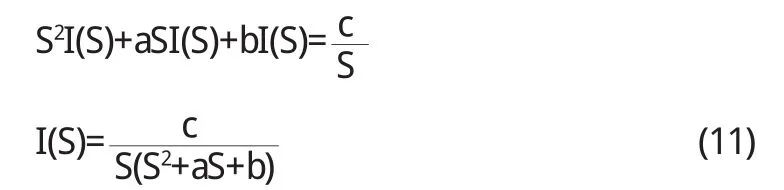
讨论：⑴若方程S2+aS+b=0有两个实数根，即：R>两实根为：

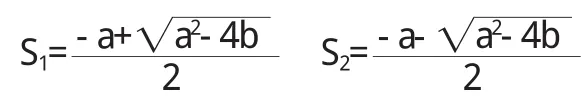
则由(11)式有：

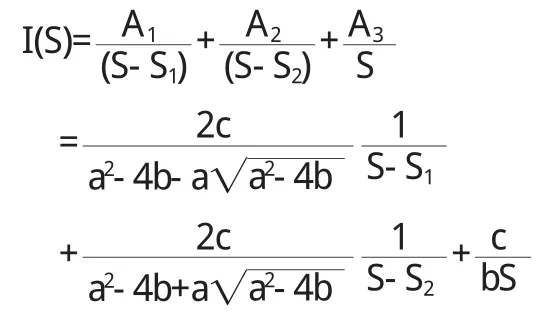
对I(S)求反拉普拉斯变换有：

由(7)式导体棒的运动速度经整理后其形式为：

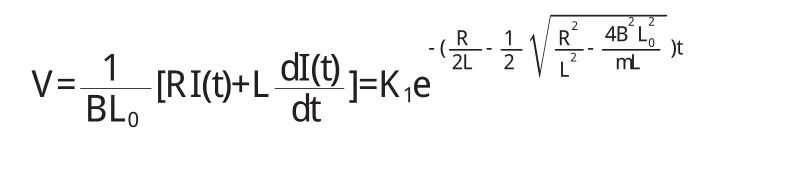
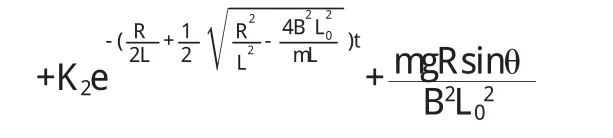
上式表明：（1）当电阻很大时，导体棒的速度单调地趋于某一定值，导体棒的运动不仅不是周期的而且不是往复的，即将导体棒释放后，将慢慢地作匀速运动.其最终速度为：

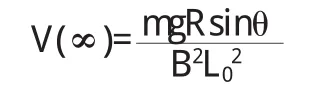
（2）若方程S2+aS+b=0有一个实数根，即其实根为：

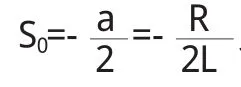
则由(11)式有：

对I(S)求反拉普拉斯变换有：

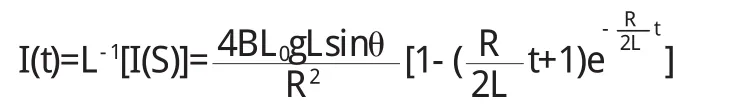
由(7)式导体棒的运动速度经整理后其形式为：

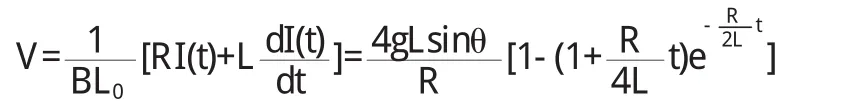
从上式可以看出导体棒的运动仍不是往复运动，将导体棒释放后，导体棒会很快达到匀速运动，其最终速度为：

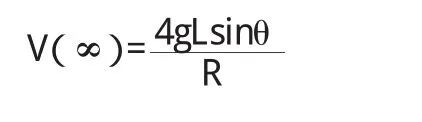
（3）若方程S2+aS+b=0有两个复数根，即其复根为：

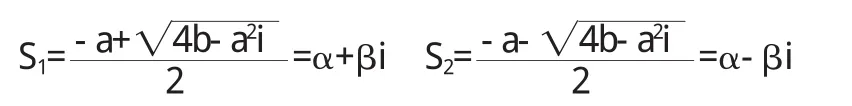
则由(11)式有：

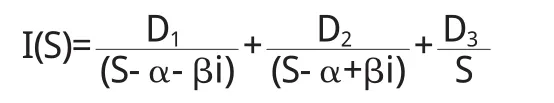
对I(S)求反拉普拉斯变换有：

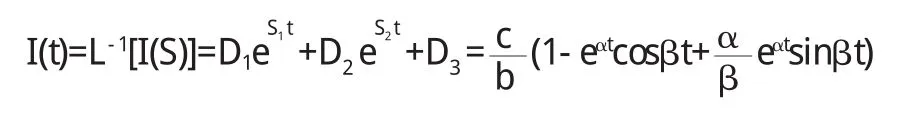
由(7)式导体棒的运动速度经整理后其形式为：

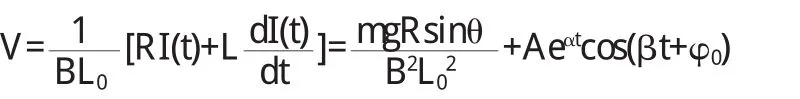
上式表明，当电阻很小时，导体棒的速度可理解为匀速直线运动与振幅按指数规律减小的周期运动的合运动，α越大，振幅减少的越快.

讨论：（1）导体棒的最终速度为

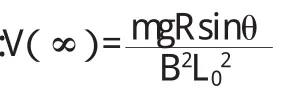
（2）若回路中电阻不计，即R=0，则导体棒将作简谐振动.

由以上的分析可知，接电阻、电容和电感时导体棒的运动规律是不同的，对于接电阻时，最终导体棒将作匀速直线运动；接电容时，导体棒最终将作匀加速直线运动，而接电感时，根据电阻的不同，导体棒最终也将作匀速直线运动.

〔1〕数学手册[M].北京：高等教育出版社.

〔2〕贺洪江,王振涛.电路基础[M].北京：高等教育出版社.

O441

A

1673-260X（2014）06-0015-02