运用龚伯兹曲线构造收入分布模型
2014-07-21曹建莉赵梦亚
曹建莉,赵梦亚
(河南工业大学 理学院, 河南 郑州450001)
运用龚伯兹曲线构造收入分布模型
曹建莉,赵梦亚
(河南工业大学 理学院, 河南 郑州450001)
本文采用适当的曲线直接拟合洛伦兹曲线来建立人口度量模型,从而使居民收入分配的公平程度得到定量的描述.其主要思想是:运用改造后的龚伯兹(Gompertz)曲线来拟合收入分布函数进而推算出洛伦兹曲线以建立新模型,并与其它10种模型以均方误差(MSE)和平均绝对误差(MAE)及最大绝对误差(MAS)为标准,运用matlab软件对各个模型的拟合精度进行计算并比较,结果显示所建新模型的拟合情况是最好的.
龚伯兹曲线;洛伦兹曲线;收入分布
1 引言
居民收入分配关系到广大民众的生活水平,分配公平程度是社会各界广泛关注的话题.我国处于经济转型期,收入分配格局处于重要的调整期,合理的收入分配格局正处于形成阶段.因此,监控收入分配格局的变化是经济社会发展的重要课题.
2 模型的建立与检验
2.1 模型的建立
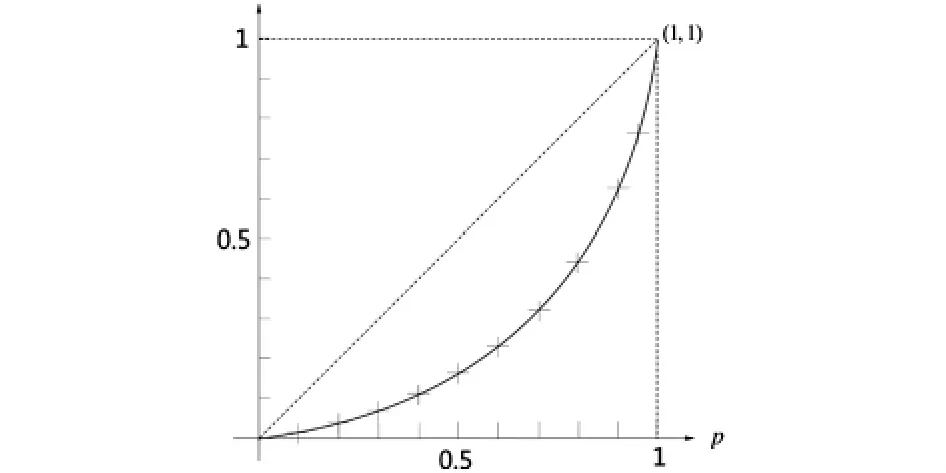
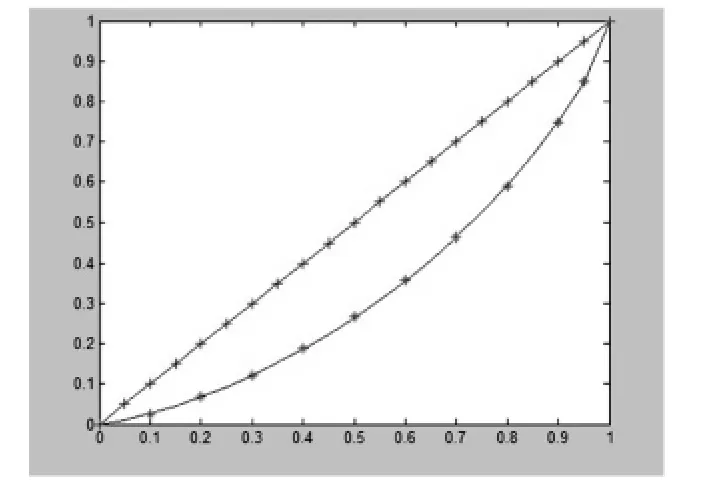
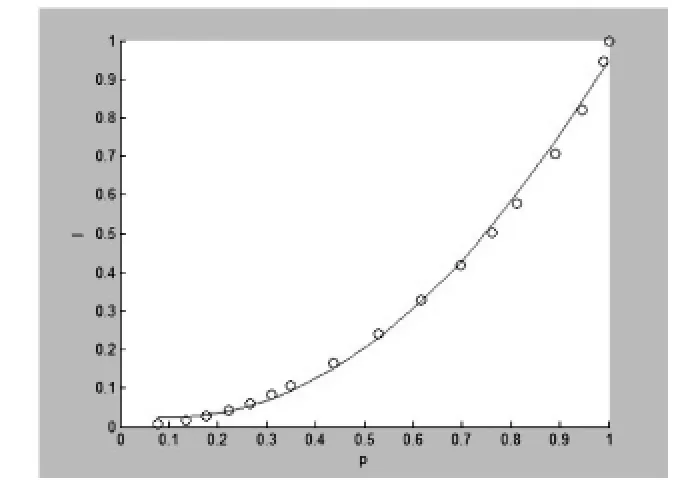
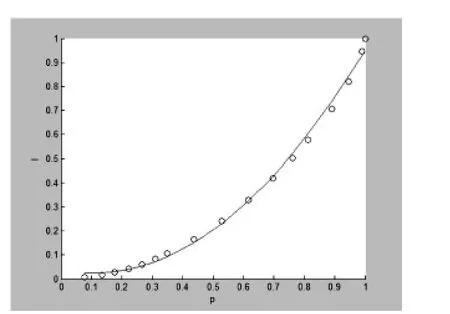
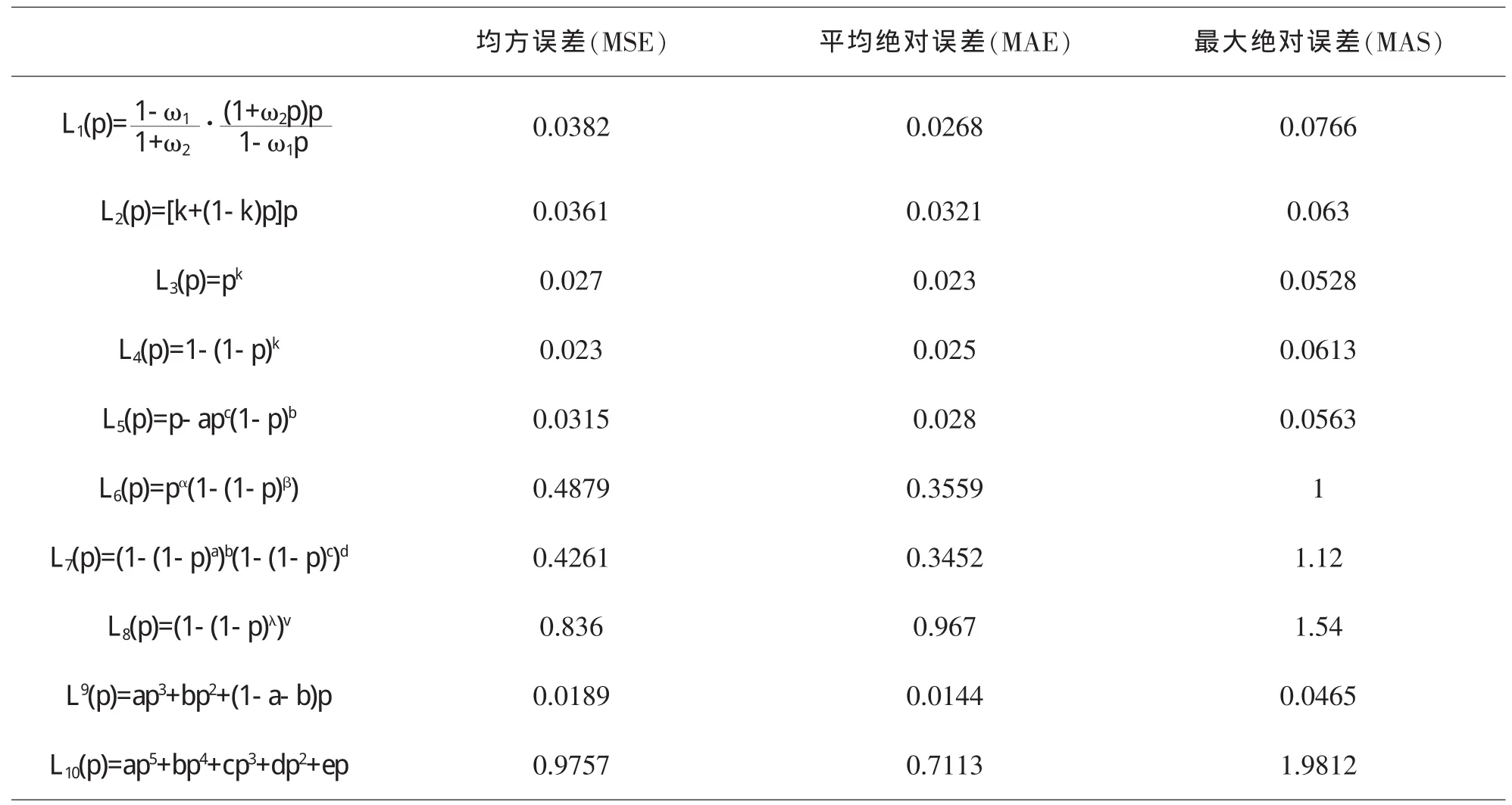
假定收入区间R为[0,+∞),收入随机变量x∈R的分布函数为F(x),须满足如下条件:①当时x∈(0,+∞),0 为了使得收入分布具有函数形式且满足上述条件,我们借鉴龚伯兹分布Y(x).该分布函数满足微分方程: 其中c为常数项.为了使得收入分布函数具有较好的拟合效果以及对数据的“自适应”能力,我们改造龚伯兹分布,将式中的常数c替换为待估函数w(x),有 求解式(2)可得 (3)具有参数估计的形式,且满足收入分布条件①,②和③.则问题转化为对W(x)的估计,为了体现收入分布Y(x)的“自适应”能力,我们采用样条拟合W(x),将结果代入式(3)可计算出收入分布函数. 将得到的收入分布函数通过求导和积分得到收入密度函数和洛伦兹曲线,进而计算基尼系数.将(3)式关于x求导,可得收入密度函数为 根据收入分布函数和洛伦兹曲线的对应关系,设收入累积比率为纵轴,人口累积比率P为横轴的曲线图形如图1. 图1 洛伦兹曲线图 这里“人口累积比率”为收入分布函数Y(x),“收入累积比率”可表示为,其中为期望收入.则洛伦兹曲线为: 其中:2.2模型的拟合检验 前人用来描绘洛伦兹曲线的方程有很多,我们通过现有的文献找出10种洛伦兹曲线的模型如下: 图2 (a) 新建模型拟合函数图像 图2 (c)对比模型三拟合函数图像 模型的拟合情况如下, 为确定拟合精度的好坏,我们分别采用以下三种标准进行比较. 均方误差(MSE,mean squared error): 平均绝对误差(MAE,mean absolute error): 最大绝对误差(MAS,maximum absolute error) 均方误差(MSE,mean squared error):指参数估计值与参数真值之差平方的期望值,MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度;平均绝对误差(MAE,mean absolute error):是所有单个观测值与算术平均值的偏差的绝对值平均.与平均误差相比,平均绝对误差由于离差被绝对值化,不会出现正负相抵消的情况,平均绝对误差能更好地反映预测值误差的实际情况;拟合情况如图2(a)、图2(b)、图2(c)和图2(d). 图2 (b) 对比模型一拟合函数图像 图2 (d)对比模型六拟合函数图像 文献中10种模型的拟合度结果见表1,通过比较可知我们新建的模型拟合优度最好.文中的参数估计,方程的拟合,以及误差的计算,均由matlab软件完成. 表1 10种模型的拟合检验 为拟合给定数据的洛伦兹曲线,我们先用龚伯兹(Gompertz)函数拟合收入分布函数,再用拟合的分布函数推导出洛伦兹曲线.经检验,该方法拟合出的洛伦兹曲线精确度比较高. 〔1〕Foster,J.E.and M.C.Wolfson,2009.Polarization and the decline of the middle class:Canada and the U.S. Journal of Economic Inequality 8,247-273. 〔2〕Wang,Z.X.,Y-K Ng,and R.Smyth,2011.A general method for creating Lorenz curves.The Review of Income and Wealth 57,561-582. 〔3〕Wang,Z.X.and R.Smyth,A hybrid method for creating Lorenz curves with an application to measuring world income inequality.,2013. 〔4〕张奎 ,王原君.Sarabia洛伦兹曲线模型的推广[J].应用数学,2010,23(3):501-507. 〔5〕黄恒军,刘黎明.一种收入分布函数序列的拟合方法及扩展应用[J].统计与信息论坛,2011,26(12):174-181. O242 A 1673-260X(2014)06-0006-03 本文的工作受到河南省教育科学“十二五”规划项目[2012]-JKGHAB-0027和河南工业大学教学研究项目的支持和资助,在此表示感谢
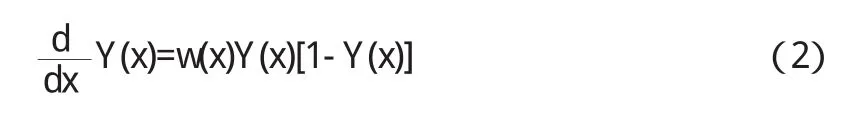

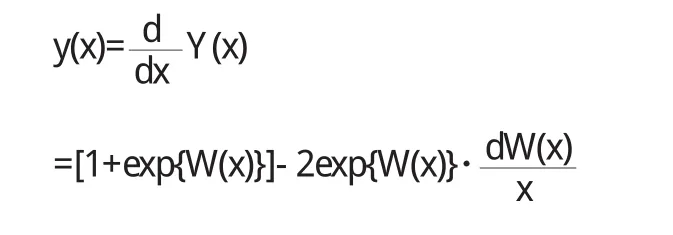
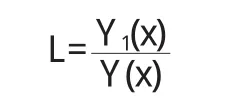
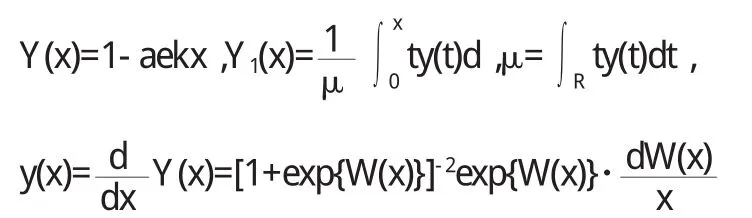
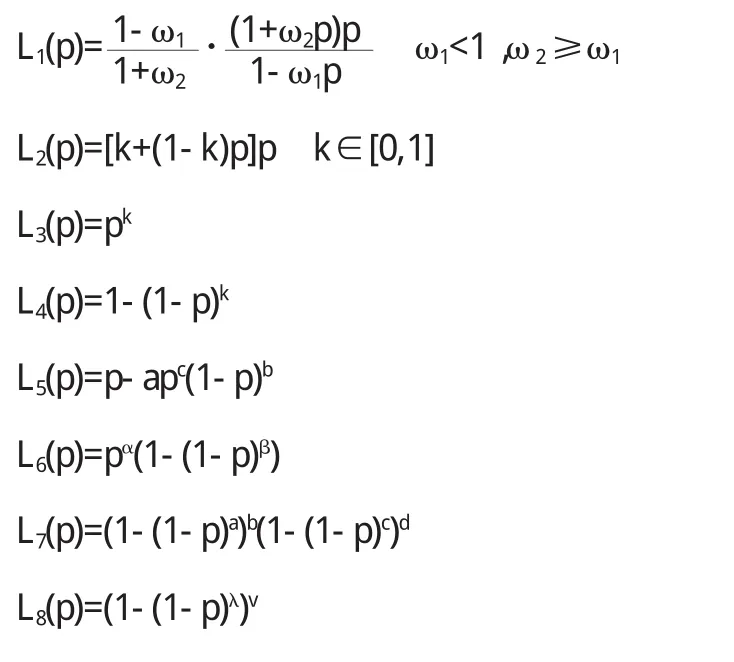
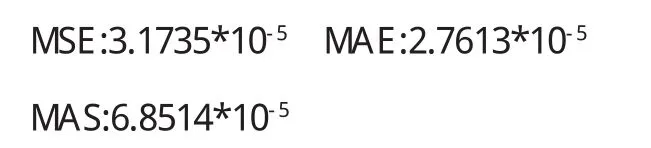
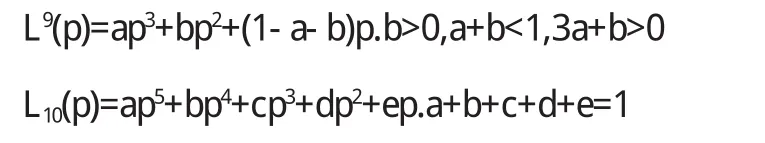
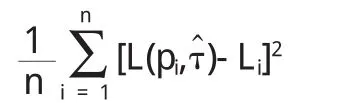
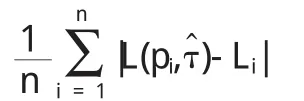
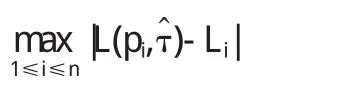

3 结论
