浅谈辅助线在几何证题中的应用

德力根仓

（赤峰学院 数学与统计学院， 内蒙古 赤峰024000）

浅谈辅助线在几何证题中的应用

德力根仓

（赤峰学院 数学与统计学院， 内蒙古 赤峰024000）

在几何证题中,当证明过程受阻时,科学合理的添加辅助线能使解题思路顺利畅通,辅助线能巧妙地连接起已知和未知,成为解题的桥梁，从而使几何证题中隐蔽的条件明朗化,为顺利地证明几何题创造条件.本文从四个方面阐述了做辅助线的方法,并举例说明在具体情况下,如何做辅助线.

辅助线；几何证题；方法

1 前言

在高中数学的讲解过程中，如何做辅助线，是几何证题中的一个重要知识点.在空间几何图形中添加辅助线，不但考验学生的空间想象能力，也考察了学生的创造性思维.做辅助线是一种难度很大的解题技巧，因为它没有法则可循，千变万化，使初学者感到特别困难.

为了帮助学生学好几何，科学正确的做出辅助线，本文分析了辅助线在几何证题中的应用，以期对开拓学生的解题思路，提高学生的分析能力、解决问题的能力以及综合运用知识的能力起到指导作用，同时力求对培养学生的逻辑思维和发散思维起到积极作用，下面主要从四个方面探讨辅助线在几何证题中的应用.

2 当几何证明题适用“综合法”时,用综合法证题，在已知推证结论思路受阻时,可从图形的特征入手,巧设辅助线,利用图形的性质继续推证

例1梯形ABCD中，已知DC∥AB,DC

求证

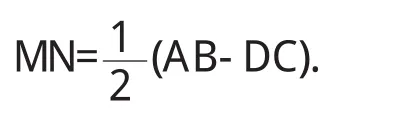
用综合法分析,题中有条件∠A+∠B=90°.如果能做一条辅助线,使∠A和∠B在同一个三角形中，即可出现直角三角形,并且题中有中点,可利用直角三角形斜边的中线等于斜边的一半的性质,来证明此题.通过C点做CE∥AD（图1），交AB与E，则可得∠CEB=90°（∠CEB=∠A，∠A+∠B=90°）,再把MN移至直角三角形CBE中，过点C做CF∥MN,交AB于F.

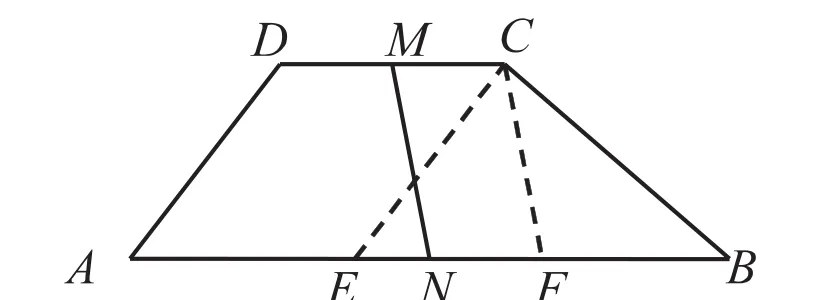
图1

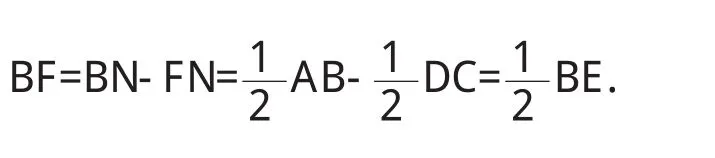
根据“直角三角形斜边上的中线等于斜边的一半”,有

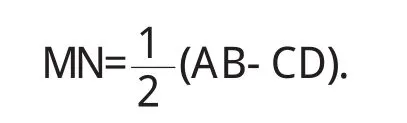
证 在梯形ABCD中,由于AD∥EC,所以

∠A+∠B=90°.又因为∠A=∠CEB,所以

∠CEB+∠B=90°.即△CEB为直角三角形.因为BE=AB-DC，所以

3 当几何证明题适用“分析法”时，用分析法证题，从结论出发，寻找结论成立的条件，难以进行下去的时候，可以添加辅助线，使追溯过程顺利进行下去

例2设 △ABC中 ∠C=2∠B,a，b，c分 别 为∠A，∠B，∠C所对的边.

求证 （a+b）b=c2.

分析 欲证（a+b）b=c2，只要证即可，为了证明,可以寻找两个相似的三角形，而它们的对应边，刚巧能成为上面的比例.若一个三角形的两边分别为b和c，则另一个三角形与之相对应的边应该为c和（a+b）.

在原图中，不存在两个三角形，没有具有（a+b）为边长的三角形.若不做辅助线，分析就无法进行下去，命题就不能获得证明.在原图中有一个△ABC,AC=b,AB=c,要得到另一个相应的三角形,其一边若为c,则必须使其另一个边为(a+b)，所以自然地会使我们想到，只要引长AC至D，并使CD=a，则AD=a+b.若再连接BD，则既可得到一个新的△ABD.在△ABD中，AB=c，AD=a+b，若再能证得,△ABC与△ADB相似,分析就可以继续进行下去了(图2).，则只要证△ABC与△ADB相似即可.

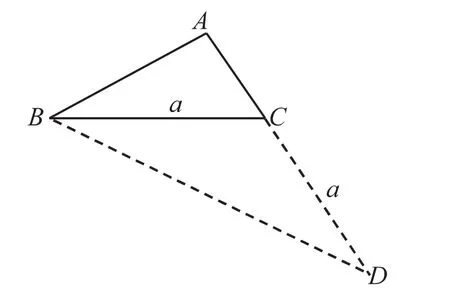
图2

因为这两个三角形有一个公共角，即∠A=∠A，因此只要能证得另一对对应角相等即可.

证 由题设知∠C=2∠B（即∠ACB=2∠ABC）.而 ∠ACB=∠D+∠CBD,BC=CD=a.∠D=∠CBD⇒∠ACB=2∠ABC⇒ ∠ABC=∠D⇒ △ABC与 ⇒△ADB相似⇒

显然，若要证得

4 辅助线可以对原几何图形进行各种变换，把已知图形的某一部分通过平移、翻转和旋转变换出所需图形，使题设中的元素与结论中的元素集中起来，元素一集中，相互之间的关系就会显露出来

例3在四边形ABCD中，AB=CD,E，F各为BC、AD的中点，BA、EF、CD相交而成∠α、∠β(图 3).

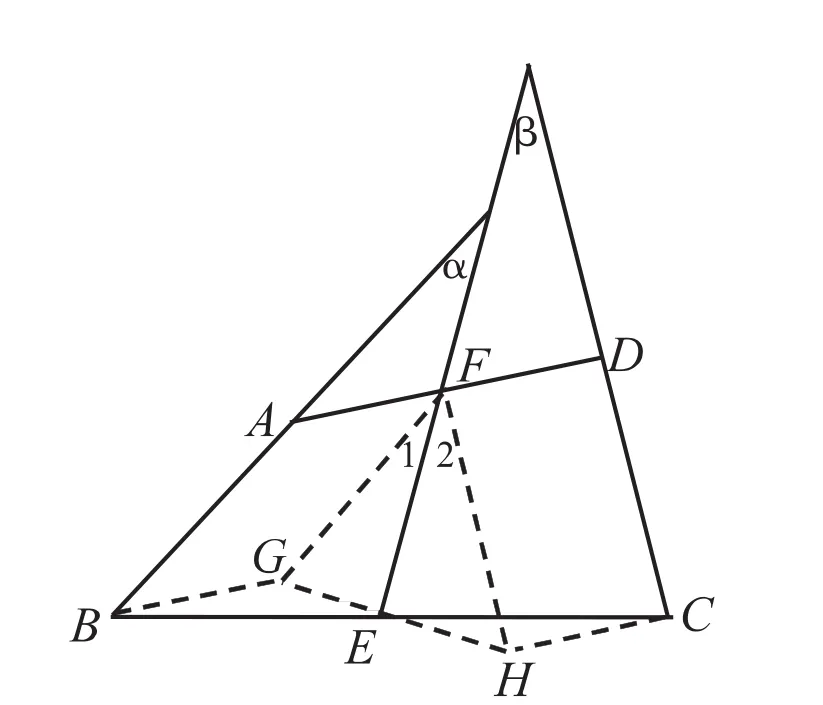
图3

求证 ∠α=∠β.

证 对题设进行分析，因BA和CD延长以后不一定刚好相交在延长线上的某一点，也就是说∠α与∠β不一定是具有共同顶点的两角.

显然，在原图要直接证明∠α=∠β 是有困难的.

为此，对部分图形做平移变换，把∠α与∠β的顶点通过平行移动集中到一个已知点上，与此同时，将AB和CD也平行移动在一起，拼成一个角的两边.于是，我们可以做出如下的辅助线.

过F作FG平行且等于AB,作FH平行且等于CD.连接EG,EH,BG和GC.这时已经把已知的元素和结论的元素集中在一起了，它们之间的关系也就显露出来.为了证明∠A=∠B,只要证明∠1=∠2即可.AB平行且等于FG,所以ABGF是平行四边形,从而BG平行且等于AF.又因为FH平行且等于DC,所以FHCD是平行四边形,从而HC平行且等于FD.由于AF=FD,所以BG平行且等于HC，因此BGCH为平行四边形.因为E为其一条对角线的中点,GEH必为另一条对角线,进而得出△FHG为等腰三角形（FG=AB，FH=CD，而AB=CD，∴FG=FH）.又因为GE=EH（因为BGCH为平行四边形）,所以FE为△FGH底边上之中线⇒FE也必为其顶角GFH之平分线⇒∠1=∠2⇒∠α=∠β.

5 通过做辅助线改造原图形或转换原 “求证”,化难为简，使隐蔽的关系明朗化

例4设△ABC的两条高线是BD和CE,其外接圆圆心为O.

求证OA⊥ED.

分析 欲证OA⊥ED，在原图上似乎很难着手，它们的交点并不是什么特殊点，于是想到做辅助线.在OA和ED中，其中OA为O圆的半径.因为半径端点的切线必与半径垂直，于是想到过A点作圆O的切线AF.

欲证OA⊥ED,只要证明AF⊥ED即可.

从而把题设中要证明的垂直关系转化为证明平行的关系了（在转化中运用了已知元素间的关系和特点），并且这个平行关系的证明有AE可以做媒介，再转化为证角的关系，只要证∠FAE=∠AED即可,于是可以得到证明的方法.

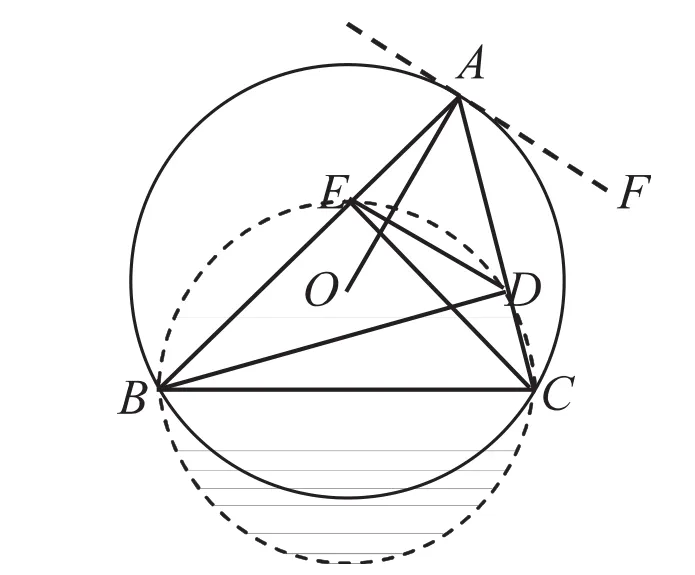
图4

证 题设中BD、CE均为△ABC的高(图4).因此∠BED=∠BDC=90°.若以BC为直径作圆，则D、E必在此辅助圆上即B、C、D、E四点共圆,所以∠AED=∠BCA.而AF是过A点的O圆切线⇒∠FAE=∠BCA⇒∠FAE=AED⇒AF∥ED.但OA⊥AF,所以OA⊥ED.

6在做辅助线的时候常常会出现下列错误，在做题时要注意,尤其是初学者更应该重视

1.没有目的乱做辅助线，不但不会对解题起到帮助，反而会造成图形混乱，影响思考.

2.做辅助线时，如果不按照基本作图法进行作图，往往会导致逻辑上的错误.下面举一个高考题说明.

例5 AB是半圆的直径,C是半圆上的一个点，直线MN切半圆与C点，AM⊥MN与M点，BN⊥MN与N点，CD⊥AB与D点(图5).

求证(1)CD=CM=CN；(2)CD2=AM·BN.

图5

有些学生在做题时错误的写到：“做∠A的平分线AC”.这就违反了作图的基本方法.做∠A的平分线，就不能保证它一定通过C点，除非予以证明.在没有依据的前提下不要乱做辅助线，否则不但对解题没有帮助，反而会造成图形混乱.

做辅助线的方法因题而异，千变万化，没有一定的法则可以遵循.这个困难在反复练习、仔细分析、研究探索后才能逐步解决，只有通过不断做题、总结、积累才能使学生做好辅助线，提高解题的能力.

〔1〕李淑华.承德民族师专学报[J].2009，29（2）.

〔2〕王长明.怎样添加平面几何辅助线[J].中国致公出版社,2003.

〔3〕严济慈.几何证题法[M].北京：高等教育出版社, 1983.

〔4〕袁晓东.浅谈几何辅助线[M].北京：北京师范大学出版社,1984.

O123；G633

A

1673-260X（2014）06-0264-03