基于时变自回归模型与神经网络的滚动轴承故障智能诊断
2014-07-21谢三毛
谢三毛
(华东交通大学 机电工程学院,南昌 330013)
在机械故障诊断领域,将各种信号处理方法与神经网络相结合是当前研究热点。时变自回归 (Time Varying Autoregressive, TVAR) 模型在时间序列自回归建模的基础上发展起来,非常适合于处理非平稳信号[1],下文将TVAR模型与神经网络相结合,用于滚动轴承故障智能诊断。
1 TVAR建模原理与时变参数估计
1.1 TVAR建模原理
TVAR过程也称为时变线性预测,其利用先前值xt-i估计当前值xt,数学表达式为
(1)
式中:ai(t)为时变系数,i=1,2,…,p;p为模型阶数;et为模型残差(均值为零,方差为σ2的白噪声)。为了对轴承振动的非平稳信号进行TVAR建模,必须选择合适的模型阶数p,确定模型的时变系数ai(t)。
1.2 基于基函数算法的TVAR时变参数估计
1.2.1 时变参数求解[2]
(1)式中时变参数ai(t)是一组基函数的线性组合,可表示为
(2)
式中:m为扩展维数;aij为基函数组合的权值;gj(t)为一组时间基函数。为求解时变参数,令
AT=(a10,…,a1m,…,ap0,…,apm),
(3)
式中:AT为1×p(m+1)矩阵;aij为基函数组合的权值,j=0,1,…,m。令
…,xt-pgm(t)],
(4)

从而可将(1)式表达为最小二乘的形式
(5)
et与xt维数相同,将一个标量过程替换成向量,从而将线性非平稳问题转化成线性时不变问题。
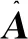
(6)

(7)
进而可以求得模型残差et的方差σ2的最小二乘估计值为
(8)
1.2.2 基函数的选择
如果时变过程的先验知识是已知的,选择基函数时要保持参数变化的趋势;如果时变过程的先验知识是未知的,基函数的选择需使得估计模型不断逼近真实模型[3]。对于轴承故障信号,信号特征是未知的,因此采用Fourier基函数进行TVAR 模型参数估计。
1.3 模型参数确定
实际应用中,通常需要根据观测数据确定模型的阶次。AIC准则(Akaike Information Criterion)[4]是目前应用比较广泛的定阶方法,即最小化最终预测误差的定阶准则,在轴承故障诊断中能够提供可靠的阶数选择,其数学表达式为
(11)
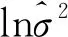
使用基函数求解时变自回归模型的时变参数和模型阶数时,模型的扩展维数m会对模型的阶数p产生影响,一般模型的扩展维数取值范围为8~12[5]。本次研究过程中发现扩展维数对模型最佳阶数的影响并不大,因此,选择扩展维数为10。
2 滚动轴承故障特征提取
2.1 数据采集
采用DH5922N型动态信号测试系统采集MDT-3A型多功能振动试验台上的轴承振动信号。轴承型号为6204,内径20 mm,外径47 mm。用特种方法分别在外圈内表面、内圈外表面加工出宽4 mm的沟槽,并在钢球表面加工出直径3 mm的凹坑来模拟轴承故障。试验的采样频率为10 kHz,每种模式各采集数据20 480点。截取连续的1 024点为一组,每种模式各得到20组数据,共获得80组轴承振动信号数据,用于神经网络训练和诊断。
2.2 模型阶数分析
使用Fourier基函数进行TVAR建模,采用AIC准则进行定阶,可以得到轴承4种模式的预选阶数与AIC值的关系,如图1所示。
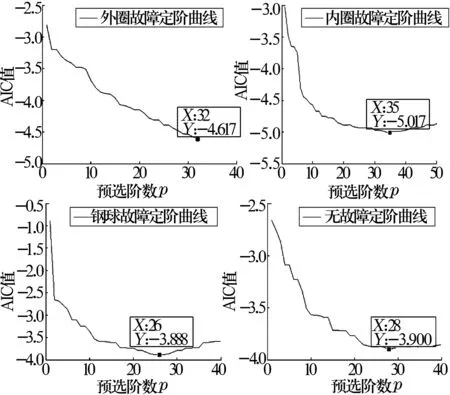
图1 轴承各种模式建模定阶曲线
从定阶曲线图上可以看出,外圈故障模式下建模分析的最佳阶数是32,此时AIC值最小,为-4.617;内圈故障模式下建模分析的最佳阶数是35,此时AIC值最小,为-5.017;钢球故障模式下建模分析的最佳阶数是26,此时AIC值最小,为-3.888;在无故障模式下建模分析的最佳阶数是28,此时AIC值最小,为-3.900。
2.3 基于TVAR模型时变参数特征提取
时变参数可作为故障诊断的特征参数,对每种模式得到的20组数据进行参数化特征提取。由于轴承的4种故障模式振动信号适应的TVAR模型阶数存在一定的差异,经多次试验,发现模型阶数为30时故障识别率最高,在此基础上提取的特征样本值见表1。
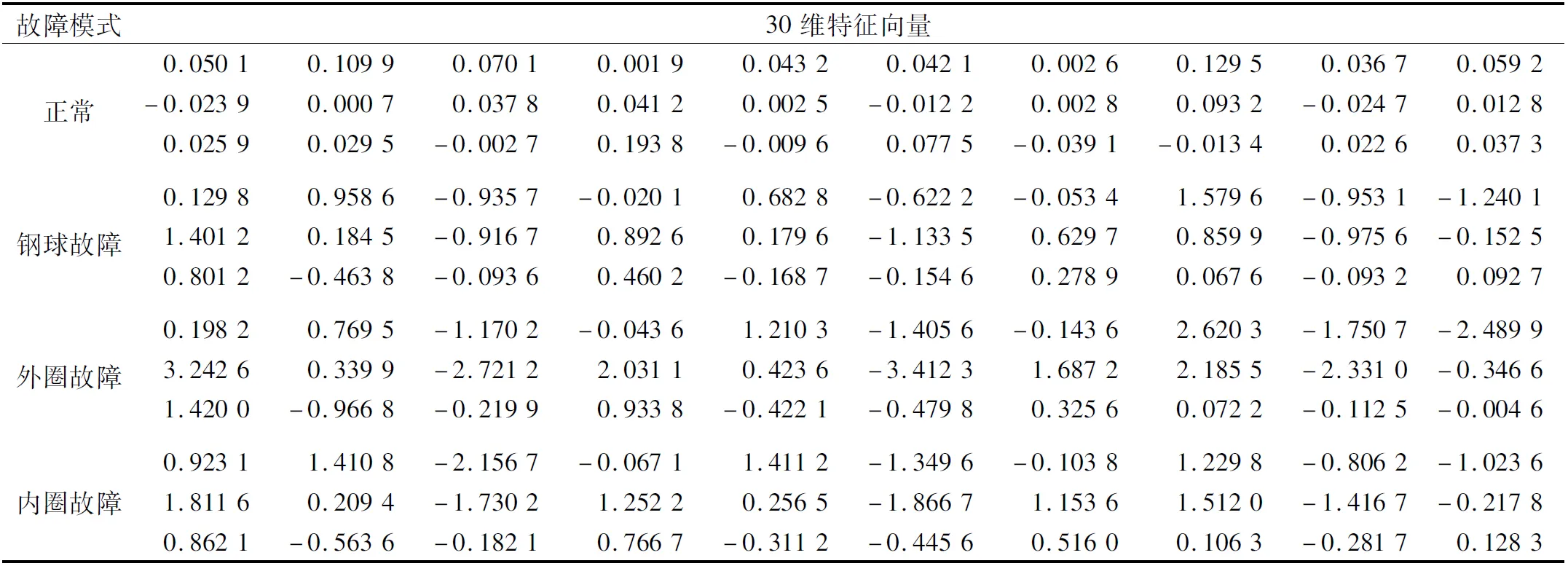
表1 时变参数特征向量
3 基于BP神经网络的智能诊断
3.1 BP神经网络结构设计
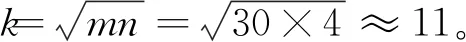
3.2 BP神经网络训练
轴承故障诊断前,必须按照一定规则[7]对BP神经网络进行训练。网络训练输入样本采用4种模式(正常、内圈故障、外圈故障和钢球故障)下包括表1在内的各10组时变参数特征向量,共40组,训练输出目标为(1 0 0 0),(0 1 0 0),(0 0 1 0)和(0 0 0 1),网络训练成功后进行保存。
3.3 诊断测试
在LabVIEW和MATLAB环境下开发滚动轴承智能诊断系统,主要功能包括:轴承振动信号获取、在线或离线分析、基于TVAR与神经网络的智能诊断、查询与保存诊断记录等。诊断系统获取数据后,可得到基于TVAR模型的时变参数特征值和基于神经网络诊断结果,如图2所示。将4种模式下剩余的40 组数据分别输入诊断系统,诊断结果见表2。
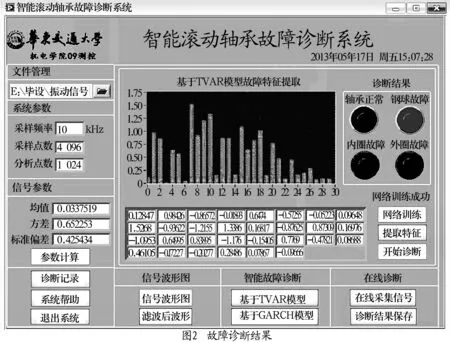
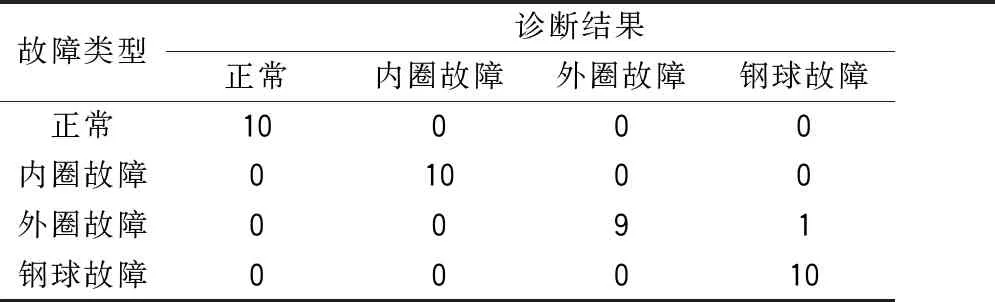
表2 故障诊断结果
从诊断结果可以看出,只有外圈故障的1组数据被错误诊断为钢球故障,总体故障识别率达到了97.5%,说明基于TVAR模型和BP神经网络诊断方法的准确率很高。
4 结束语
TVAR模型的时变参数能很好地表示轴承故障的特征,可以取得较好的信号处理效果,将其与BP神经网络结合可以有效地诊断出轴承故障部位。
